人教版七上1.2.4绝对值(第一课时) 课件(共25张PPT)
文档属性
| 名称 | 人教版七上1.2.4绝对值(第一课时) 课件(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-24 09:03:03 | ||
图片预览







文档简介
(共25张PPT)
1.2.4绝对值(第一课时)
人教版七年级上册
教学目标
1.理解绝对值的概念及其几何意义,通过从数、形两个方面理解绝对值的意义,初步了解数形结合的思想方法;
2.会求一个数的绝对值,知道一个数的绝对值,会求这个数;
3.通过应用绝对值解决实际问题,培养学生的学习兴趣,提高学生对数学的好奇心和求知欲.
教学重点:
1.理解绝对值几何意义和绝对值的性质及其代数的表示方法.
教学难点
1.会求一个数的绝对值和知道一个数的绝对值,求这个数
2.绝对值化简及简单计算.
新知导入
●
O
●
A
10
●
B
-10
0
甲、乙两辆汔车从同一处O出发,分别向东、向西行驶10km,到达A、B两处.
思考:1.两辆汔车的行驶路线相同吗?
行驶路线不相同,甲汽车向东行驶,乙汽车向西行驶.
新知导入
●
O
●
A
10
●
B
-10
0
甲、乙两辆汔车从同一处O出发,分别向东、向西行驶10km,到达A、B两处.
思考:2.它们的行驶路程相同吗?
10
10
点A(甲汽车)表示在原点O右侧,且与原点距离为10个单位长度;
点B(乙汽车)表示在原点O左侧,且与原点距离为10个单位长度;
所以甲、乙两辆汔车行驶路程相等.
新知讲解
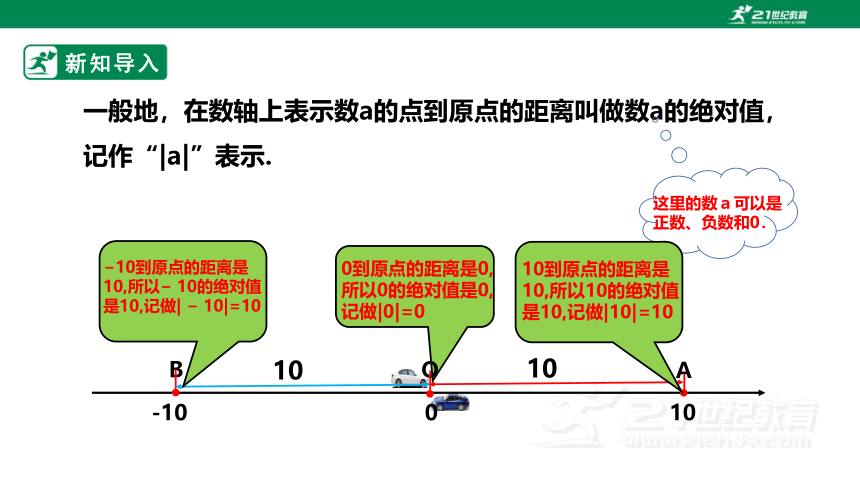
一般地,在数轴上表示数a的点到原点的距离叫做数a的绝对值,记作“|a|”表示.
绝对值的定义
绝对值的符号: .
“| |”
|a|读法:
数a的绝对值
0到原点的距离是0,所以0的绝对值是0,记做|0|=0
新知导入
●
O
●
A
10
●
B
-10
0
10
10
一般地,在数轴上表示数a的点到原点的距离叫做数a的绝对值,记作“|a|”表示.
这里的数a可以是正数、负数和0.
10到原点的距离是10,所以10的绝对值是10,记做|10|=10
10到原点的距离是10,所以 10的绝对值是10,记做| 10|=10
新知讲解
例1.求下列各数的绝对值:
运算结果与原数有什么关系?你有何发现?
解:
| |=
| |=
| |=
|12|=
| |=
|0|=
||=
新知讲解
| |=
| |=
| |=
| 12 |=
| |=
|0|=
| | =
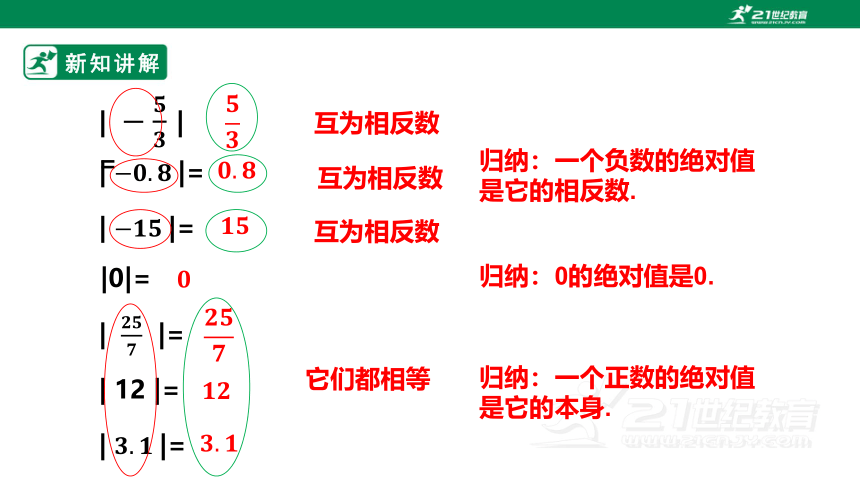
互为相反数
互为相反数
互为相反数
归纳:一个负数的绝对值是它的相反数.
归纳:0的绝对值是0.
它们都相等
归纳:一个正数的绝对值是它的本身.
归纳
一个正数的绝对值是它本身,一个负数的绝对值是它的相反数,0的绝对值是0. 即
(1)如果 a>0,那么|a|=___;
(2)如果 a=0, 那么|a|=___;
(3)如果 a<0,那么|a|=___.
a
0
a
即:|a|=
a (a>0)
0 (a=0)
a (a<0)
(正数的绝对值是它本身.)
(负数的绝对值是它的相反数.)
(0的绝对值是0.)
(任一有理数的绝对值是一个非负数.)
|a|≥0
新知讲解
互为相反数的两个数与它们的绝对值有什么关系
| |=
| |=
互为相反数的两个数的绝对值相等.
绝对值相等,符号相反的两个数互为相反数.
练一练
1.填空:求下列各数的绝对值.
||= ;
| |= ;
| 3 |= ;
| 0 |= .
||= ;
2.若|x|=2 022,则x=________.
正数的绝对值是它本身.
负数的绝对值是它的相反数.
0的绝对值是0.
负数的绝对值是它的相反数.
正数的绝对值是它本身.
±2 022
新知讲解
例2(1)绝对值是9的数有几个各是什么
(2)绝对值是0的数有几个 各是什么
(3)有没有绝对值是 1的数 为什么
分析:根据绝对值的定义解答.
(3)没有绝对值是 1的数,因为任何有理数的绝对值都是非负数.
解:(1)绝对值是9的数有2个,是+9和 9.
(2)绝对值是0的数有1个,是0.
归纳
例题小结:
1.绝对值等于一个正数的数有两个,这两个数互为相反数;
2.互为相反数的两个数的绝对值相等;
3.绝对值等于0的数只有一个,就是0;
4.没有绝对值等于负数的数.
新知讲解
例3(1)有理数a,b,c在数轴上的对应点的位置如图所示,这三个数中,绝对值最大的是 ;
(2)若|a 3|+|b 5|=0,则a= ,b= .
0
1 2 3 4
4 3 2 1
(2)因为|a 3|+|b 5|=0, |a 3|≥0,|b 5| ≥ 0
解:(1)由绝对值的定义可知,点b离原点最远,故点b绝对值最大.
所以a=3,b=5.
所以a 3=0 , b 5=0
归纳
例题小结:
1.绝对值越大的数对应的点离原点越远,反之,绝对值越小的数对应的点离原点越近,0的绝对值最小.
2. 若几个数绝对值之和为0,则这几个数同时为0,即若|a|+|b|=0 ,则a=b=0;
练一练
(1)有理数a,b,c在数轴上的对应点的位置如图所示,这三个数中,绝对值最大的是 ;
(2)若|a 1|+|b 2|=0,则a+b= .
0
1 2 3 4
4 3 2 1
分析:(2)因为|a 1|+|b 2|=0, |a 1|≥0,|b 2| ≥ 0
所以a=1,b=2, a+b=3.
所以a 1=0 , b 2=0
课堂练习
1. 若x为任意有理数, 则 | x |一定是( )
A.正数或零 B.负数
C.负数或零 D.正数
2. 2022的绝对值为( ).
A. 2020 B. 2020 C. D.
C
A
课堂练习
3. 下列各式不成立的是( ).
A. | 5|=5 B. | 5|= |5|
C. | 5|= |5| D. | 5|=5
D
4.若|a|+|b|=0,则a与b的大小关系是( )
A. a与b不相等 B.a与b互为倒数
C.a与b异号 D. a=b=0
D
课堂练习
5. 填空:
(1). 0.1的相反数是_____, 0.1的绝对值是______.
(2). |2022|=______,|0|=_____,| 13|=______.
(3). 5的绝对值是______,绝对值等于3的数是______.
(4). | 2|=______,+| 20|=_______, |+20|=______.
(5). 1的相反数的绝对值等于 ,2的绝对值的相反数是 .
1
2
0.1
0.1
2022
0
13
5
±3
2
20
20
课堂练习
6.已知有理数a,b满足等式|a-7|+ |b-1|=0,则a= ,b= .
7.绝对值不大于2的整数是 .
7
1
2, 1,0,1,2,
课堂练习
8. 若a,b各表示一个理数, |a|=1,|b|=| 3|,求在数轴上, 数a,b对应的点之间的距离.
解:因为|a|=1,|b|=| 3|
所以a=1或 1 , b=3或 3.
①当a=1 , b=3时, a,b对应的点之间的距离为2.
②当a=1 , b= 3时, a,b对应的点之间的距离为4.
③当a= 1 , b=3时, a,b对应的点之间的距离为4.
④当a= 1 , b= 3时, a,b对应的点之间的距离为2.
课堂总结
一个正数的绝对值是它本身,一个负数的绝对值是它的相反数,0的绝对值是0. 即
即:|a|=
a (a>0)
0 (a=0)
a (a<0)
(正数的绝对值是它本身.)
(负数的绝对值是它的相反数.)
(0的绝对值是0.)
(任一有理数的绝对值是一个非负数.)
|a|≥0
一般地,在数轴上表示数a的点到原点的距离叫做数a的绝对值,记作“|a|”表示.
1.绝对值的概念:
2.绝对值的性质及应用
作业布置
第14页习题1.2
第5题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
1.2.4绝对值(第一课时)
人教版七年级上册
教学目标
1.理解绝对值的概念及其几何意义,通过从数、形两个方面理解绝对值的意义,初步了解数形结合的思想方法;
2.会求一个数的绝对值,知道一个数的绝对值,会求这个数;
3.通过应用绝对值解决实际问题,培养学生的学习兴趣,提高学生对数学的好奇心和求知欲.
教学重点:
1.理解绝对值几何意义和绝对值的性质及其代数的表示方法.
教学难点
1.会求一个数的绝对值和知道一个数的绝对值,求这个数
2.绝对值化简及简单计算.
新知导入
●
O
●
A
10
●
B
-10
0
甲、乙两辆汔车从同一处O出发,分别向东、向西行驶10km,到达A、B两处.
思考:1.两辆汔车的行驶路线相同吗?
行驶路线不相同,甲汽车向东行驶,乙汽车向西行驶.
新知导入
●
O
●
A
10
●
B
-10
0
甲、乙两辆汔车从同一处O出发,分别向东、向西行驶10km,到达A、B两处.
思考:2.它们的行驶路程相同吗?
10
10
点A(甲汽车)表示在原点O右侧,且与原点距离为10个单位长度;
点B(乙汽车)表示在原点O左侧,且与原点距离为10个单位长度;
所以甲、乙两辆汔车行驶路程相等.
新知讲解
一般地,在数轴上表示数a的点到原点的距离叫做数a的绝对值,记作“|a|”表示.
绝对值的定义
绝对值的符号: .
“| |”
|a|读法:
数a的绝对值
0到原点的距离是0,所以0的绝对值是0,记做|0|=0
新知导入
●
O
●
A
10
●
B
-10
0
10
10
一般地,在数轴上表示数a的点到原点的距离叫做数a的绝对值,记作“|a|”表示.
这里的数a可以是正数、负数和0.
10到原点的距离是10,所以10的绝对值是10,记做|10|=10
10到原点的距离是10,所以 10的绝对值是10,记做| 10|=10
新知讲解
例1.求下列各数的绝对值:
运算结果与原数有什么关系?你有何发现?
解:
| |=
| |=
| |=
|12|=
| |=
|0|=
||=
新知讲解
| |=
| |=
| |=
| 12 |=
| |=
|0|=
| | =
互为相反数
互为相反数
互为相反数
归纳:一个负数的绝对值是它的相反数.
归纳:0的绝对值是0.
它们都相等
归纳:一个正数的绝对值是它的本身.
归纳
一个正数的绝对值是它本身,一个负数的绝对值是它的相反数,0的绝对值是0. 即
(1)如果 a>0,那么|a|=___;
(2)如果 a=0, 那么|a|=___;
(3)如果 a<0,那么|a|=___.
a
0
a
即:|a|=
a (a>0)
0 (a=0)
a (a<0)
(正数的绝对值是它本身.)
(负数的绝对值是它的相反数.)
(0的绝对值是0.)
(任一有理数的绝对值是一个非负数.)
|a|≥0
新知讲解
互为相反数的两个数与它们的绝对值有什么关系
| |=
| |=
互为相反数的两个数的绝对值相等.
绝对值相等,符号相反的两个数互为相反数.
练一练
1.填空:求下列各数的绝对值.
||= ;
| |= ;
| 3 |= ;
| 0 |= .
||= ;
2.若|x|=2 022,则x=________.
正数的绝对值是它本身.
负数的绝对值是它的相反数.
0的绝对值是0.
负数的绝对值是它的相反数.
正数的绝对值是它本身.
±2 022
新知讲解
例2(1)绝对值是9的数有几个各是什么
(2)绝对值是0的数有几个 各是什么
(3)有没有绝对值是 1的数 为什么
分析:根据绝对值的定义解答.
(3)没有绝对值是 1的数,因为任何有理数的绝对值都是非负数.
解:(1)绝对值是9的数有2个,是+9和 9.
(2)绝对值是0的数有1个,是0.
归纳
例题小结:
1.绝对值等于一个正数的数有两个,这两个数互为相反数;
2.互为相反数的两个数的绝对值相等;
3.绝对值等于0的数只有一个,就是0;
4.没有绝对值等于负数的数.
新知讲解
例3(1)有理数a,b,c在数轴上的对应点的位置如图所示,这三个数中,绝对值最大的是 ;
(2)若|a 3|+|b 5|=0,则a= ,b= .
0
1 2 3 4
4 3 2 1
(2)因为|a 3|+|b 5|=0, |a 3|≥0,|b 5| ≥ 0
解:(1)由绝对值的定义可知,点b离原点最远,故点b绝对值最大.
所以a=3,b=5.
所以a 3=0 , b 5=0
归纳
例题小结:
1.绝对值越大的数对应的点离原点越远,反之,绝对值越小的数对应的点离原点越近,0的绝对值最小.
2. 若几个数绝对值之和为0,则这几个数同时为0,即若|a|+|b|=0 ,则a=b=0;
练一练
(1)有理数a,b,c在数轴上的对应点的位置如图所示,这三个数中,绝对值最大的是 ;
(2)若|a 1|+|b 2|=0,则a+b= .
0
1 2 3 4
4 3 2 1
分析:(2)因为|a 1|+|b 2|=0, |a 1|≥0,|b 2| ≥ 0
所以a=1,b=2, a+b=3.
所以a 1=0 , b 2=0
课堂练习
1. 若x为任意有理数, 则 | x |一定是( )
A.正数或零 B.负数
C.负数或零 D.正数
2. 2022的绝对值为( ).
A. 2020 B. 2020 C. D.
C
A
课堂练习
3. 下列各式不成立的是( ).
A. | 5|=5 B. | 5|= |5|
C. | 5|= |5| D. | 5|=5
D
4.若|a|+|b|=0,则a与b的大小关系是( )
A. a与b不相等 B.a与b互为倒数
C.a与b异号 D. a=b=0
D
课堂练习
5. 填空:
(1). 0.1的相反数是_____, 0.1的绝对值是______.
(2). |2022|=______,|0|=_____,| 13|=______.
(3). 5的绝对值是______,绝对值等于3的数是______.
(4). | 2|=______,+| 20|=_______, |+20|=______.
(5). 1的相反数的绝对值等于 ,2的绝对值的相反数是 .
1
2
0.1
0.1
2022
0
13
5
±3
2
20
20
课堂练习
6.已知有理数a,b满足等式|a-7|+ |b-1|=0,则a= ,b= .
7.绝对值不大于2的整数是 .
7
1
2, 1,0,1,2,
课堂练习
8. 若a,b各表示一个理数, |a|=1,|b|=| 3|,求在数轴上, 数a,b对应的点之间的距离.
解:因为|a|=1,|b|=| 3|
所以a=1或 1 , b=3或 3.
①当a=1 , b=3时, a,b对应的点之间的距离为2.
②当a=1 , b= 3时, a,b对应的点之间的距离为4.
③当a= 1 , b=3时, a,b对应的点之间的距离为4.
④当a= 1 , b= 3时, a,b对应的点之间的距离为2.
课堂总结
一个正数的绝对值是它本身,一个负数的绝对值是它的相反数,0的绝对值是0. 即
即:|a|=
a (a>0)
0 (a=0)
a (a<0)
(正数的绝对值是它本身.)
(负数的绝对值是它的相反数.)
(0的绝对值是0.)
(任一有理数的绝对值是一个非负数.)
|a|≥0
一般地,在数轴上表示数a的点到原点的距离叫做数a的绝对值,记作“|a|”表示.
1.绝对值的概念:
2.绝对值的性质及应用
作业布置
第14页习题1.2
第5题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
