12.2全等三角形判定(一) 学案
文档属性
| 名称 | 12.2全等三角形判定(一) 学案 |  | |
| 格式 | zip | ||
| 文件大小 | 29.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-09-18 13:12:13 | ||
图片预览

文档简介
课题:12.2全等三角形判定(一) 课型:预习+展示 主备人: 审核人: 小主人姓名:
*学习目标*:1.能知道“边边边”的内容,会运用“SSS”证明三角形全等,为证明线段相等或角相等创造条件;知道三角形的稳定性;3.经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程。*学习重点*:会运用“SSS”证明三角形全等。*学习难点*:能运用“SSS”证明三角形全等。
学习过程 学法指导
*知识回顾*什么是全等三角形?全等三角形的性质?把△ABC绕点A逆时针旋转,边AB旋转到AD,得到△ADE,用符号“≌”表示图中与△ABC全等的三角形,并写出它们的对应边和对应角.二. *能力生成*活动一 探索三角形全等的条件1.只给一个条件:(1)画出一条边为6cm 三角形 (2) 画出一个角为30度的三角形.小组交流所画的三角形全等吗?2.给出两个条件画三角形时,有几种可能的情况?分别按照下面条件, 用刻度尺或量角器画三角形,并和小组的同学比较一下,所画的图形全等吗 ①三角形的一个内角为60°,一条边为3 cm;② 三角形的两个内角分别为30°和70°;③ 三角形的两条边分别为3 cm和5 cm从1、2画图归纳:如果只知道两个三角形有一个或两个对应相等的部分(边或角),那么这两个三角形 . 自学时要有“三动”眼动、手动、脑动!注意双色笔的使用哦!独学课本内容。有疑惑可以与对子商讨,或者小组讨论。在讨论的过程中,注意总结规律。
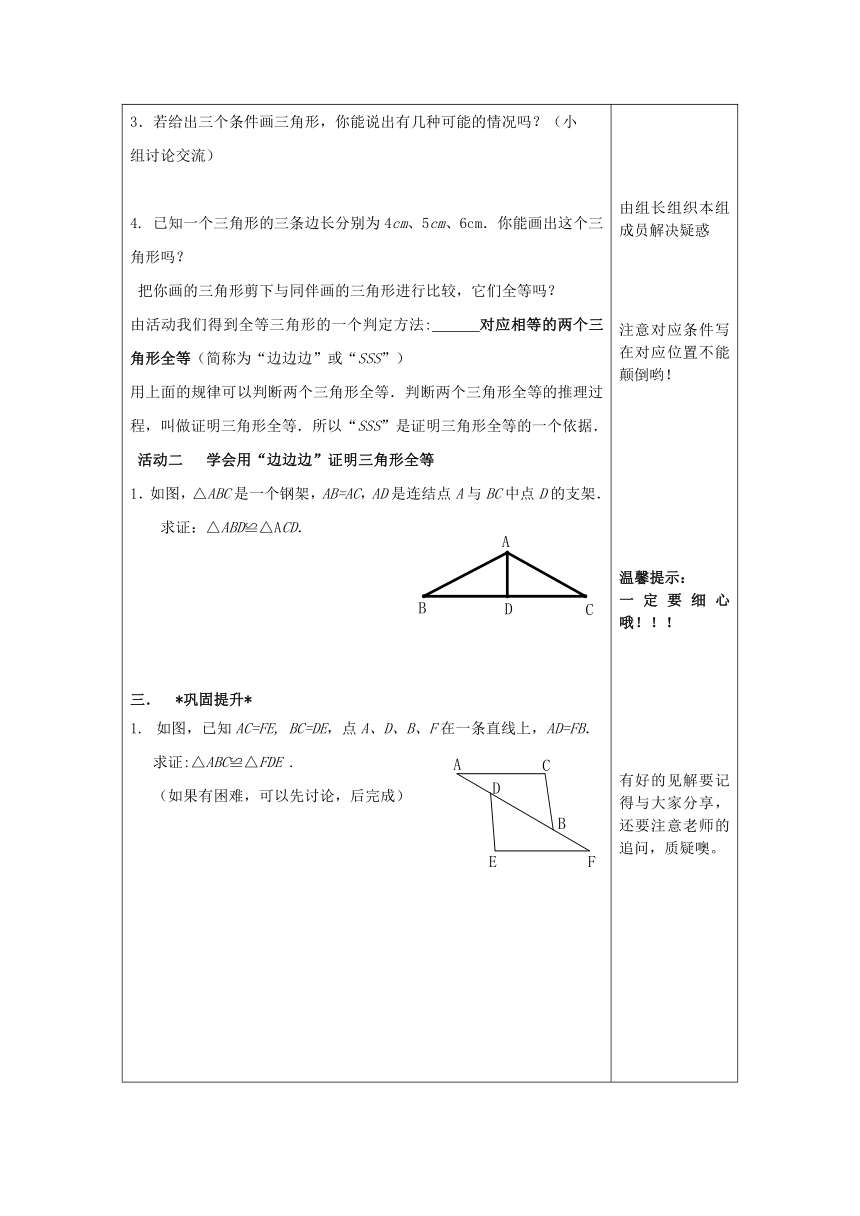
3.若给出三个条件画三角形,你能说出有几种可能的情况吗?(小组讨论交流)4. 已知一个三角形的三条边长分别为4cm、5cm、6cm.你能画出这个三角形吗?把你画的三角形剪下与同伴画的三角形进行比较,它们全等吗?由活动我们得到全等三角形的一个判定方法: 对应相等的两个三角形全等(简称为“边边边”或“SSS”)用上面的规律可以判断两个三角形全等.判断两个三角形全等的推理过程,叫做证明三角形全等.所以“SSS”是证明三角形全等的一个依据.活动二 学会用“边边边”证明三角形全等1.如图,△ABC是一个钢架,AB=AC,AD是连结点A与BC中点D的支架.求证:△ABD≌△ACD.三. *巩固提升*如图,已知AC=FE, BC=DE,点A、D、B、F在一条直线上,AD=FB.求证:△ABC≌△FDE .(如果有困难,可以先讨论,后完成) 由组长组织本组成员解决疑惑注意对应条件写在对应位置不能颠倒哟!温馨提示:一定要细心哦!!!有好的见解要记得与大家分享,还要注意老师的追问,质疑噢。
求证:△ABC≌△CDA.
★★2.如图,,,△ABC≌△DCB全等吗?为什么? ★★★3.如图,一个六边形钢架ABCDEF由6条钢管连结而成,为使这一钢架稳固,请你用三条钢管连接使它不能活动,和同伴交流看看方法是否一样. ★.相信自己,我能完成★★超越自己,我要完成★★★挑战自己,我最棒学以致用不亦乐乎!
如图,AB=AC,BD=CD,那么∠B与∠C是否相等?为什么? 总结自己本节课的收获,将易错题整理在纠错本上,以备复习使用
A
B
E
C
D
神马都是浮云,只会做题还不行,如果我们能将这种能力用于实际生活中,我才真正获得了能力,咱们走着瞧。
A
B
C
D
*学习目标*:1.能知道“边边边”的内容,会运用“SSS”证明三角形全等,为证明线段相等或角相等创造条件;知道三角形的稳定性;3.经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程。*学习重点*:会运用“SSS”证明三角形全等。*学习难点*:能运用“SSS”证明三角形全等。
学习过程 学法指导
*知识回顾*什么是全等三角形?全等三角形的性质?把△ABC绕点A逆时针旋转,边AB旋转到AD,得到△ADE,用符号“≌”表示图中与△ABC全等的三角形,并写出它们的对应边和对应角.二. *能力生成*活动一 探索三角形全等的条件1.只给一个条件:(1)画出一条边为6cm 三角形 (2) 画出一个角为30度的三角形.小组交流所画的三角形全等吗?2.给出两个条件画三角形时,有几种可能的情况?分别按照下面条件, 用刻度尺或量角器画三角形,并和小组的同学比较一下,所画的图形全等吗 ①三角形的一个内角为60°,一条边为3 cm;② 三角形的两个内角分别为30°和70°;③ 三角形的两条边分别为3 cm和5 cm从1、2画图归纳:如果只知道两个三角形有一个或两个对应相等的部分(边或角),那么这两个三角形 . 自学时要有“三动”眼动、手动、脑动!注意双色笔的使用哦!独学课本内容。有疑惑可以与对子商讨,或者小组讨论。在讨论的过程中,注意总结规律。
3.若给出三个条件画三角形,你能说出有几种可能的情况吗?(小组讨论交流)4. 已知一个三角形的三条边长分别为4cm、5cm、6cm.你能画出这个三角形吗?把你画的三角形剪下与同伴画的三角形进行比较,它们全等吗?由活动我们得到全等三角形的一个判定方法: 对应相等的两个三角形全等(简称为“边边边”或“SSS”)用上面的规律可以判断两个三角形全等.判断两个三角形全等的推理过程,叫做证明三角形全等.所以“SSS”是证明三角形全等的一个依据.活动二 学会用“边边边”证明三角形全等1.如图,△ABC是一个钢架,AB=AC,AD是连结点A与BC中点D的支架.求证:△ABD≌△ACD.三. *巩固提升*如图,已知AC=FE, BC=DE,点A、D、B、F在一条直线上,AD=FB.求证:△ABC≌△FDE .(如果有困难,可以先讨论,后完成) 由组长组织本组成员解决疑惑注意对应条件写在对应位置不能颠倒哟!温馨提示:一定要细心哦!!!有好的见解要记得与大家分享,还要注意老师的追问,质疑噢。
求证:△ABC≌△CDA.
★★2.如图,,,△ABC≌△DCB全等吗?为什么? ★★★3.如图,一个六边形钢架ABCDEF由6条钢管连结而成,为使这一钢架稳固,请你用三条钢管连接使它不能活动,和同伴交流看看方法是否一样. ★.相信自己,我能完成★★超越自己,我要完成★★★挑战自己,我最棒学以致用不亦乐乎!
如图,AB=AC,BD=CD,那么∠B与∠C是否相等?为什么? 总结自己本节课的收获,将易错题整理在纠错本上,以备复习使用
A
B
E
C
D
神马都是浮云,只会做题还不行,如果我们能将这种能力用于实际生活中,我才真正获得了能力,咱们走着瞧。
A
B
C
D
