第五单元信息窗1《异分母分数的大小比较》(课件)-五年级下册数学 青岛版(15张PPT 用wps打开)
文档属性
| 名称 | 第五单元信息窗1《异分母分数的大小比较》(课件)-五年级下册数学 青岛版(15张PPT 用wps打开) |

|
|
| 格式 | zip | ||
| 文件大小 | 13.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-22 00:00:00 | ||
图片预览






文档简介
(共15张PPT)
异分母分数的大小比较
某市在实施“垃圾分类”工程中对生活垃圾种类进行了统计。
其中厨房垃圾占 ,菜叶果皮占 ,废纸占 ,玻璃占 .
从图中你发现了哪些数学信息?
根据这些数学信息你能提出比较分数大小的数学问题吗?
请同学们借助已有的知识经验来解决这个问题,先自己独立思考把你的想法写在探究单上,再把你的方法和依据在小组里交流。
想一想怎样做可以比较 和 的大小?
= 2÷5=0.4
= 1÷2=0.5
因为0.4﹤0.5
所以 ﹤
=
因为 ﹤
所以 ﹤
= =
= =
因为 ﹤
所以 ﹤
仔细观察这三种方法,想一想它们有什么相同点?
化小数
化同分子
化同分母
=
=
=
=
异分母分数
同分母分数
分数单位不同
分数单位相同
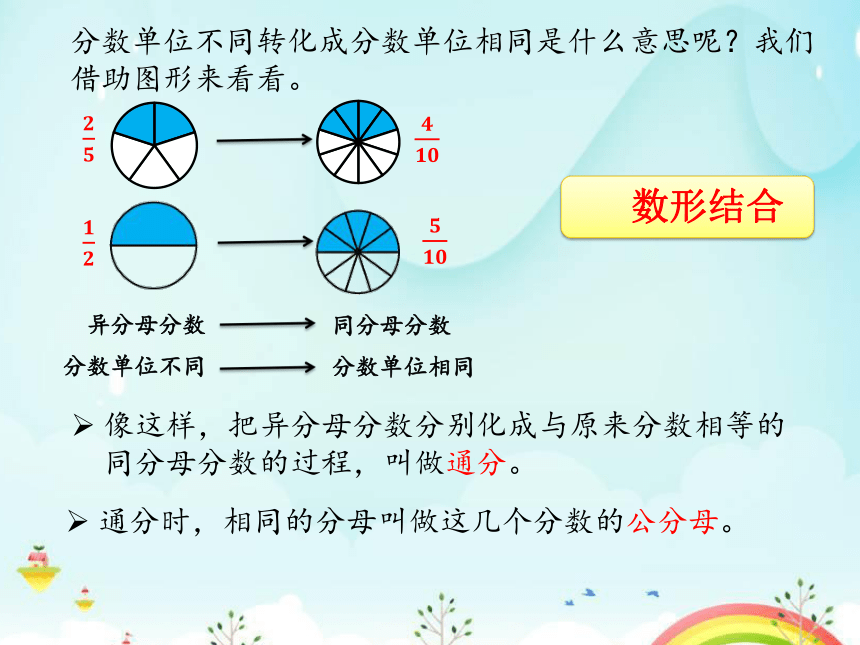
分数单位不同转化成分数单位相同是什么意思呢?我们借助图形来看看。
像这样,把异分母分数分别化成与原来分数相等的同分母分数的过程,叫做通分。
通分时,相同的分母叫做这几个分数的公分母。
数形结合
判断下面哪一组是通分?
= =
= =
= =
= =
= =
= =
1
2
3
√
你会把 和
把下列各组分数通分
和
和
和
=
=
=
=
=
=
=
=
=
=
=
比较每组分数的大小
>
>
>
<
拓展练习:
1.越野比赛中,王明用小时跑完全程,李强用 小时跑完全程,谁跑得快?
2.跑步比赛中,用同样的时间,王珊跑了千米,李娜跑了千米,谁跑得快?
= =
= =
答:李强跑得快。
= =
= =
>
答:王珊跑得快。
路程一定,谁用的时间少谁快
时间一定,谁跑的距离多谁快
“同而通之”: , , 通分方法,找到2,3,5的最小公倍数30,再把 , , 进行一次通分,转化成 , , .是所谓的“同而通之”。
“通而同之”: , , 通分方法,先找到2和3的最小公倍数6,把 , 分别转化成 , ,再找6和5的最小公倍数30,进而把 , , 分别转化为 , , ,通过两次通分,最后将三个分数都统一成分母是30的分数,这是所谓的“通而同之”。
你有哪些收获?
异分母分数的大小比较
某市在实施“垃圾分类”工程中对生活垃圾种类进行了统计。
其中厨房垃圾占 ,菜叶果皮占 ,废纸占 ,玻璃占 .
从图中你发现了哪些数学信息?
根据这些数学信息你能提出比较分数大小的数学问题吗?
请同学们借助已有的知识经验来解决这个问题,先自己独立思考把你的想法写在探究单上,再把你的方法和依据在小组里交流。
想一想怎样做可以比较 和 的大小?
= 2÷5=0.4
= 1÷2=0.5
因为0.4﹤0.5
所以 ﹤
=
因为 ﹤
所以 ﹤
= =
= =
因为 ﹤
所以 ﹤
仔细观察这三种方法,想一想它们有什么相同点?
化小数
化同分子
化同分母
=
=
=
=
异分母分数
同分母分数
分数单位不同
分数单位相同
分数单位不同转化成分数单位相同是什么意思呢?我们借助图形来看看。
像这样,把异分母分数分别化成与原来分数相等的同分母分数的过程,叫做通分。
通分时,相同的分母叫做这几个分数的公分母。
数形结合
判断下面哪一组是通分?
= =
= =
= =
= =
= =
= =
1
2
3
√
你会把 和
把下列各组分数通分
和
和
和
=
=
=
=
=
=
=
=
=
=
=
比较每组分数的大小
>
>
>
<
拓展练习:
1.越野比赛中,王明用小时跑完全程,李强用 小时跑完全程,谁跑得快?
2.跑步比赛中,用同样的时间,王珊跑了千米,李娜跑了千米,谁跑得快?
= =
= =
答:李强跑得快。
= =
= =
>
答:王珊跑得快。
路程一定,谁用的时间少谁快
时间一定,谁跑的距离多谁快
“同而通之”: , , 通分方法,找到2,3,5的最小公倍数30,再把 , , 进行一次通分,转化成 , , .是所谓的“同而通之”。
“通而同之”: , , 通分方法,先找到2和3的最小公倍数6,把 , 分别转化成 , ,再找6和5的最小公倍数30,进而把 , , 分别转化为 , , ,通过两次通分,最后将三个分数都统一成分母是30的分数,这是所谓的“通而同之”。
你有哪些收获?
