人教A版2019必修第一册4.4.3 不同函数增长的差异 课件(共21张PPT)
文档属性
| 名称 | 人教A版2019必修第一册4.4.3 不同函数增长的差异 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-23 07:55:05 | ||
图片预览







文档简介
(共21张PPT)
4.4 对数函数
4.4.3 不同函数增长的差异
复习导入
在前面的学习中我们看到,一次函数与指数函数的增长方式存在很大差异.事实上,这种差异正是不同类型现实问题具有不同增长规律的反映.因此,如果把握了不同函数增长方式的差异,那么就可以根据现实问题的增长情况,选择合适的函数模型刻画其变化规律.下面就来研究一次函数、指数函数和对数函数增长方式的差异.
活动1:请同学们选取适当的指数函数与一次函数,探索它们在区间上的增长差异,你能描述一下指数函数的特点吗?不妨以函数和为例.(学生做草图)
为了更好地研究它们的增长差异,我们利用信息技术,列出上述两个函数的自变量与函数值的对应值表,并在同一个直角坐标系中画出它们的图象.
新知探索
新知探索
可以看到,函数和的图象有两个交点.
0 1 0
0.5 1.414 1
1 2 2
1.5 2.828 3
2 4 4
2.5 5.657 5
3 8 6
… … …
新知探索
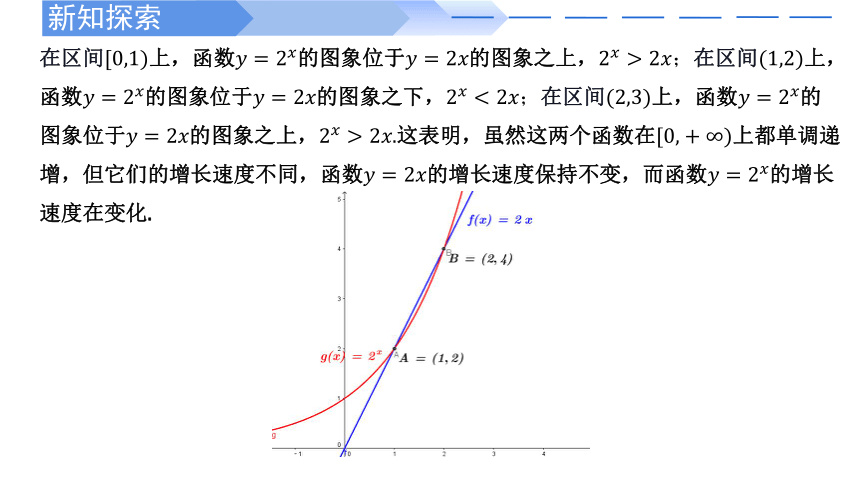
在区间上,函数的图象位于的图象之上,;在区间上,函数的图象位于的图象之下,;在区间上,函数的图象位于的图象之上,这表明,虽然这两个函数在上都单调递增,但它们的增长速度不同,函数的增长速度保持不变,而函数的增长速度在变化.
新知探索
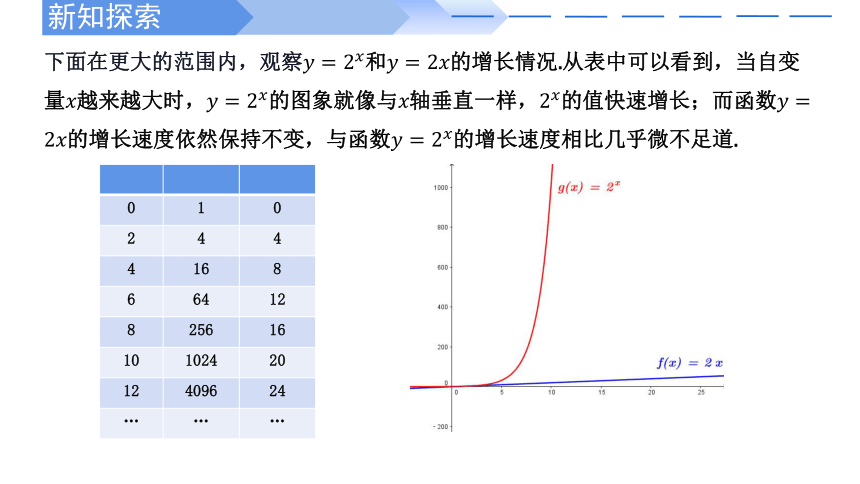
下面在更大的范围内,观察和的增长情况.从表中可以看到,当自变量越来越大时,的图象就像与轴垂直一样,的值快速增长;而函数的增长速度依然保持不变,与函数的增长速度相比几乎微不足道.
0 1 0
2 4 4
4 16 8
6 64 12
8 256 16
10 1024 20
12 4096 24
… … …
新知探索
综上所述,虽然函数和在区间上都单调递增,但它们的增长速度不同,而且不在同一个“档次”上.随着的增大,的增长速度越来越快,会超过并远远大于的增长速度.尽管在的一定变化范围内,会小于,但由于的增长最终会快于的增长,因此,总会存在一个当时,恒有.
一般地,指数函数与一次函数的增长差异都与上述情况类似.即使的值远远大于的值,的增长速度最终都会大大超过的增长速度.
注:指数函数不像一次函数那样按同一速度增长,而是越来越快,呈爆炸性增长.
新知探索
活动2:请同学们选取适当的对数函数与一次函数,探索它们在区间上的增长差异,你能描述一下对数函数的特点吗?不妨以函数和为例.(学生做草图)
为了更好地研究它们的增长差异,我们利用信息技术,列出上述两个函数的自变量与函数值的对应值表,并在同一个直角坐标系中画出它们的图象.
新知探索
可以看到,虽然它们在上都单调递增,但增长速度存在明显的差异.
0 不存在 0
10 1 1
20 1.301 2
30 1.477 3
40 1.602 4
50 1.699 5
60 1.778 6
… … …
新知探索
函数的增长速度保持不变,而函数的增长速度在变化.随着的最大,函数的图象离轴越来越远,而函数的图象越来越平缓,就像与轴平行一样.
新知探索
例如而这说明,当,即时,与相比增长就很慢了.
新知探索
活动3:如果将放大1000倍,再对函数和的增长情况进行比较,那么仍有上述规律吗?
因为函数值较大不便于手动画图,我们利用信息技术在同一个直角坐标系中画出它们的图象并研究其增长情况.
新知探索
一般地,虽然对数函数与一次函数在区间上都单调递增,但它们的增长速度不同.随着的增大,一次函数保持固定的增长速度,而对数函数的增长速度越来越慢.不论的值比的值大多少,在一定范围内,可能会大于,但由于的增长最终会慢于的增长,因此总会存在一个,当时,恒有.
新知探索
活动4:类比上述过程,
(1)画出一次函数对数函数和指数函数的图象,并比较它们的增长差异;
(2)试着概况一次函数,对数函数和指数函数的增长差异;
(3)讨论交流“直线上升”“对数增长”“指数爆炸”的含义.
新知探索
练习
题型一:三类函数模型增长差异的比较
例1.下列函数中,增长速度最快的是( ).
答案:A.一次函数、指数函数和对数函数三类函数模型中,指数增长最快.
新知探索
变1.“红豆生南国,春来发几枝”给出了红豆生长时间(月)与枝数的关系图,那么最适合拟合红豆的枝数与生长时间的关系的函数是( ).
指数函数 对数函数
幂函数 二次函数
答案:A.由图中数据可知,A选项的指数函数模型的拟合效果最好.
新知探索
题型二:函数模型的选择
例2.学校为了实现60万元的生源利润目标,准备制定一个激励招生人员的奖励方案:在生源利润达到5万元时,按生源利润进行奖励,且奖金(单位:万元)随生源利润(单位:万元)的增加而增加,但奖金总数不超过万元,同时奖金不超过利润的20%.现有三个奖励模型:其中哪个模型符合该校的要求?
新知探索
解:作出函数的图象,观察图象可知,在区间上,的图象都有一部分在直线的上方,只有的图象始终在和的下方,这说明只有按模型进行奖励才符合学校的要求.
例2.学校为了实现60万元的生源利润目标,准备制定一个激励招生人员的奖励方案:在生源利润达到5万元时,按生源利润进行奖励,且奖金(单位:万元)随生源利润(单位:万元)的增加而增加,但奖金总数不超过万元,同时奖金不超过利润的20%.现有三个奖励模型:其中哪个模型符合该校的要求?
练习
变2.某人对东北一种松树的生长进行了研究,搜集了其高度(米)与生长时间(年)的相关数据,选择与来拟合与的关系,你认为哪个符合?并预测第8年的松树高度.
解:由图表可画出图象,因此用来拟合更符合.不妨将点代入中,得:
,解得
∴,当时,求得即第8年的松树高度为2米.
(年) 1 2 3 4 5 6
(米) 0.6 1 1.3 1.5 1.6 1.7
课堂小结&作业
课堂小结:
三种函数模型的增长情况.
作业:
(1)温故本节课的三种函数模型的增长情况;
(2)课本P139的练习1--4题.
4.4 对数函数
4.4.3 不同函数增长的差异
复习导入
在前面的学习中我们看到,一次函数与指数函数的增长方式存在很大差异.事实上,这种差异正是不同类型现实问题具有不同增长规律的反映.因此,如果把握了不同函数增长方式的差异,那么就可以根据现实问题的增长情况,选择合适的函数模型刻画其变化规律.下面就来研究一次函数、指数函数和对数函数增长方式的差异.
活动1:请同学们选取适当的指数函数与一次函数,探索它们在区间上的增长差异,你能描述一下指数函数的特点吗?不妨以函数和为例.(学生做草图)
为了更好地研究它们的增长差异,我们利用信息技术,列出上述两个函数的自变量与函数值的对应值表,并在同一个直角坐标系中画出它们的图象.
新知探索
新知探索
可以看到,函数和的图象有两个交点.
0 1 0
0.5 1.414 1
1 2 2
1.5 2.828 3
2 4 4
2.5 5.657 5
3 8 6
… … …
新知探索
在区间上,函数的图象位于的图象之上,;在区间上,函数的图象位于的图象之下,;在区间上,函数的图象位于的图象之上,这表明,虽然这两个函数在上都单调递增,但它们的增长速度不同,函数的增长速度保持不变,而函数的增长速度在变化.
新知探索
下面在更大的范围内,观察和的增长情况.从表中可以看到,当自变量越来越大时,的图象就像与轴垂直一样,的值快速增长;而函数的增长速度依然保持不变,与函数的增长速度相比几乎微不足道.
0 1 0
2 4 4
4 16 8
6 64 12
8 256 16
10 1024 20
12 4096 24
… … …
新知探索
综上所述,虽然函数和在区间上都单调递增,但它们的增长速度不同,而且不在同一个“档次”上.随着的增大,的增长速度越来越快,会超过并远远大于的增长速度.尽管在的一定变化范围内,会小于,但由于的增长最终会快于的增长,因此,总会存在一个当时,恒有.
一般地,指数函数与一次函数的增长差异都与上述情况类似.即使的值远远大于的值,的增长速度最终都会大大超过的增长速度.
注:指数函数不像一次函数那样按同一速度增长,而是越来越快,呈爆炸性增长.
新知探索
活动2:请同学们选取适当的对数函数与一次函数,探索它们在区间上的增长差异,你能描述一下对数函数的特点吗?不妨以函数和为例.(学生做草图)
为了更好地研究它们的增长差异,我们利用信息技术,列出上述两个函数的自变量与函数值的对应值表,并在同一个直角坐标系中画出它们的图象.
新知探索
可以看到,虽然它们在上都单调递增,但增长速度存在明显的差异.
0 不存在 0
10 1 1
20 1.301 2
30 1.477 3
40 1.602 4
50 1.699 5
60 1.778 6
… … …
新知探索
函数的增长速度保持不变,而函数的增长速度在变化.随着的最大,函数的图象离轴越来越远,而函数的图象越来越平缓,就像与轴平行一样.
新知探索
例如而这说明,当,即时,与相比增长就很慢了.
新知探索
活动3:如果将放大1000倍,再对函数和的增长情况进行比较,那么仍有上述规律吗?
因为函数值较大不便于手动画图,我们利用信息技术在同一个直角坐标系中画出它们的图象并研究其增长情况.
新知探索
一般地,虽然对数函数与一次函数在区间上都单调递增,但它们的增长速度不同.随着的增大,一次函数保持固定的增长速度,而对数函数的增长速度越来越慢.不论的值比的值大多少,在一定范围内,可能会大于,但由于的增长最终会慢于的增长,因此总会存在一个,当时,恒有.
新知探索
活动4:类比上述过程,
(1)画出一次函数对数函数和指数函数的图象,并比较它们的增长差异;
(2)试着概况一次函数,对数函数和指数函数的增长差异;
(3)讨论交流“直线上升”“对数增长”“指数爆炸”的含义.
新知探索
练习
题型一:三类函数模型增长差异的比较
例1.下列函数中,增长速度最快的是( ).
答案:A.一次函数、指数函数和对数函数三类函数模型中,指数增长最快.
新知探索
变1.“红豆生南国,春来发几枝”给出了红豆生长时间(月)与枝数的关系图,那么最适合拟合红豆的枝数与生长时间的关系的函数是( ).
指数函数 对数函数
幂函数 二次函数
答案:A.由图中数据可知,A选项的指数函数模型的拟合效果最好.
新知探索
题型二:函数模型的选择
例2.学校为了实现60万元的生源利润目标,准备制定一个激励招生人员的奖励方案:在生源利润达到5万元时,按生源利润进行奖励,且奖金(单位:万元)随生源利润(单位:万元)的增加而增加,但奖金总数不超过万元,同时奖金不超过利润的20%.现有三个奖励模型:其中哪个模型符合该校的要求?
新知探索
解:作出函数的图象,观察图象可知,在区间上,的图象都有一部分在直线的上方,只有的图象始终在和的下方,这说明只有按模型进行奖励才符合学校的要求.
例2.学校为了实现60万元的生源利润目标,准备制定一个激励招生人员的奖励方案:在生源利润达到5万元时,按生源利润进行奖励,且奖金(单位:万元)随生源利润(单位:万元)的增加而增加,但奖金总数不超过万元,同时奖金不超过利润的20%.现有三个奖励模型:其中哪个模型符合该校的要求?
练习
变2.某人对东北一种松树的生长进行了研究,搜集了其高度(米)与生长时间(年)的相关数据,选择与来拟合与的关系,你认为哪个符合?并预测第8年的松树高度.
解:由图表可画出图象,因此用来拟合更符合.不妨将点代入中,得:
,解得
∴,当时,求得即第8年的松树高度为2米.
(年) 1 2 3 4 5 6
(米) 0.6 1 1.3 1.5 1.6 1.7
课堂小结&作业
课堂小结:
三种函数模型的增长情况.
作业:
(1)温故本节课的三种函数模型的增长情况;
(2)课本P139的练习1--4题.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
