人教A版2019必修第一册5.2.1 三角函数的概念 课件(共28张PPT)
文档属性
| 名称 | 人教A版2019必修第一册5.2.1 三角函数的概念 课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-23 07:57:20 | ||
图片预览







文档简介
(共28张PPT)
5.2 三角函数的概念
5.2.1三角函数的概念
复习导入
在上节课的学习中,我们实现了角度制与弧度制间的转化.并且利用弧度制,已经将角的范围扩展到了全体实数.
正角
零角
负角
正实数
0
负实数
复习导入
下面借助这些知识研究上一节开头提出的问题.不失一般性,先研究单位圆上点的运动.
活动1:如图,单位圆上的点以为起点做逆时针方向旋转,建立一个数学模型,刻画点的位置变化情况.
新知探索
根据研究函数的经验,我们利用直角坐标系来研究上述问题.
如图,以单位圆的圆心为原点,以射线为轴的非负半轴,建立直角坐标系,点的坐标为,点的坐标为.射线从轴的非负半轴开始,绕点按逆时针方向旋转角,终止位置为.
新知探索
Q1:当时,点的坐标是什么?
Q2:当或时,点的坐标又是什么?它们是唯一确定的吗?
Q3:一般地,任意给定一个角,它的终边与单位圆交点的坐标能唯一确定吗?
利用勾股定理可以发现,当时,点的坐标是;
当时,点的坐标是和它们都是唯一确定的.
新知探索
一般地,任意给定一个角它的终边与单位圆交点的坐标,无论是横坐标还是纵坐标,都是唯一确定的.所以,点的横坐标、纵坐标都是角的函数.下面给出这些函数的定义.
设是一个任意角,,它的终边与单位圆交点.
新知探索
1.把点的纵坐标叫做的正弦函数,记作,即
2.把点的横坐标叫做的余弦函数,记作,即
3.把点的纵坐标与横坐标的比值叫做的正切,记作,即
可以看出,当时,的终边在轴上,这是点的横坐标等于0,所以无意义.除此之外,对于确定的角,的值也是唯一确定的.所以,也是以角为自变量,以单位圆上的点的纵坐标与横坐标的比值为函数值的函数,称为正切函数.
新知探索
我们将正弦函数、余弦函数和正切函数统称为三角函数,通常将它们记为:
正弦函数
余弦函数
正切函数
在初中我们学了锐角三角函数,知道它们都是以锐角为自变量,以比值为函数值的函数.设,把按锐角三角函数定义求得的锐角的正弦记为,并把按本节三角函数定义求得的的正弦记为.我们发现与是相等的,且对于余弦、正切也有相同的结论.
例析
例1.求的正弦、余弦和正切值.
解:在直角坐标系中,作易知的终边与单位圆的交点坐标为.所以有:
例析
例2.如图,设是一个任意角,它的终边上任意一点(不与原点重合)的坐标为
,点与原点的距离为.求证:
证明:如图,设角的终边与单位圆交于交点分别过点,作轴的垂线,垂足分别为则:
,,,,
于是,,即.因为与同号,所以
即同理可得,
根据勾股定理,.由例2可知,只要知道角终边上任意一点的坐标,就可以求得角的各个三角函数值,并且这些函数值不会随点的位置的改变而改变.
新知探索
学习了三角函数的定义,接下来研究它们的一些性质.
活动2:根据任意角的三角函数定义,先将正弦、余弦、正切函数在弧度制下的定义域填入下表,再将这三种函数的值在各象限的符号填入图中的括号.
三角函数 定义域
( + )
( + )
( + )
( + )
三角函数值在各象限内的符号,我们可以简记为:“一全正二正弦三正切四余弦.”
或“全STC”.(意思是在第一象限全为正,第二象限正弦为正,第三象限正切为正,第四象限余弦为正)
( + )
+
( - )
( - )
( - )
( - )
( - )
( - )
新知探索
辨析1:判断正误.
(1)已知是三角形的内角,则必有( )
(2)若,则是第一或第二象限角.( )
(3)对于任意角,都有意义.( )
答案:√,×,×.
辨析2:若则在( ).
A.第一象限 B.第二象限 C.第三象限 D.第四象限
答案:C.
例析
例3.求证:角为第三象限角的充要条件是
证明:先证充分性,即如果式都成立,那么为第三象限角.
因为式成立,所以角的终边可能位于第三或第四象限,也可能与轴的负半轴重合;
又因为式成立,所以角的终边可能位于第一或第三象限.
因为式都成立,所以角的终边只能位于第三象限.于是角为第三象限角.
必要性,即若为第三象限角,则有且成立.
新知探索
活动3:现在我们尝试从三角函数的定义出发,讨论一下什么时候三角函数取值相等?
由三角函数的定义,可以知道:终边相同的角的同一三角函数的值相等.
由此,我们可以得到一组公式:
公式一
其中
新知探索
公式一
其中
利用公式一,可以把求任意角的三角函数值,转化为求(或0°360°)角的三角函数值.
由公式一可知,三角函数值拥有“周而复始”的变化规律,即角的终边每绕原点旋转一周,函数值将重复出现.
新知探索
辨析3:判断正误.
(1)若,则( )
(2)若,则.( )
答案:√,×.
辨析4:(1)的值是________.
(2)________.
答案:(1);(2).
例析
例4.确定下列三角函数值的符号,然后用计算工具验证:
(1)(2);(3);(4)
解:(1)因为是第三象限角,所以;
(2)因为是第四象限角,所以
(3)因为
而是第一象限角,所以>0.
(4)因为而的终边在轴上,
所以
例析
例5.求下列三角函数值:
(1)(精确到0.001);(2);(3)
解:(1);
(2)
(3).
练习
例1.已知角的终边上有一点,且,求的值.
题型一:三角函数的定义与应用
解:∵∴
又,∴∴又
∴是第一或第二象限角.
当是第一象限角时,则.
当是第二象限角时,则.
练习
变1.已知角的终边落在直线上,求的值.
解:直线,即经过第二、四象限.
在第二象限取直线上的点,则
∴,,
在第四象限取直线上的点
∴.
练习
利用三角函数的定义求角的三角函数值的类型:
(1)若已知角,则只需确定出该角的终边与单位圆的交点坐标,即可求出各三角函数值;
(2)若已知角终边上一点为单位圆上的点,则
(3)若已知角终边上一点不是单位圆上一点,则
(4)若已知角终边上点的坐标含参数,则需对其所在象限进行分类讨论.
练习
题型二:三角函数值符号的运用
例2.已知点位于第二象限,那么角所在的象限是( ).
A.第一象限 B.第二象限 C.第三象限 D.第四象限
答案:C.
由点位于第二象限,
可得,可得.
所以角所在的象限是第三象限.
变2.(1)若三角形的两内角满足,则此三角形必为( ).
A.锐角三角形 B.钝角三角形 C.直角三角形 D.以上三种情况都有可能
答案:B.三角形的两内角的终边一定落在第一、第二象限或轴正半轴上,
所以所以角为钝角,此三角形为钝角三角形.
练习
变2.(2)的符号为_______(填“正”或“负”).
答案:负.∵,,∴分别为第三、第二、第一象限角,∴∴的符号为负.
练习
有关三角函数值符号问题的解题策略:
(1)若已知角的三角函数值(,,)中任意两个的符号,可分别确定出角终边所在的可能位置,二者的公共部分即角的终边位置.注意终边在坐标轴上的特殊情况.
(2)对于多个三角函数值符号的判断问题,需进行分类讨论.
(3)对于确定角是第几象限角的问题,应先确定题目中所有三角函数值的符号,然后依据上述三角函数值的符号来确定角是第几象限角,它们的公共部分即为所求;对于已知角的终边所在的象限来判断角的三角函数值的符号问题,则常依据三角函数的定义,或利用口诀“一全正,二正弦,三正切,四余弦”来解决.
练习
题型三:诱导公式一的应用
例3.求值:
(1)(2).
解:(1)原式
(2)原式
.
变3.求下列各式的值:
(1)(2).
解:(1)原式
(2)原式
练习
练习
利用诱导公式一进行求值化简的步骤:
定形
转化
求值
将已知的任意角写成的形式,其中
根据诱导公式,转化为角的某个三角函数值
若角为特殊角,可直接求出该角的三角函数值
课堂小结&作业
课堂小结:
(1)任意角的三角函数的定义;
(2)三角函数值的符号;
(3)诱导公式一.
作业:
(1)整理本节课的题型;
(2)课本P182的练习15题.
5.2 三角函数的概念
5.2.1三角函数的概念
复习导入
在上节课的学习中,我们实现了角度制与弧度制间的转化.并且利用弧度制,已经将角的范围扩展到了全体实数.
正角
零角
负角
正实数
0
负实数
复习导入
下面借助这些知识研究上一节开头提出的问题.不失一般性,先研究单位圆上点的运动.
活动1:如图,单位圆上的点以为起点做逆时针方向旋转,建立一个数学模型,刻画点的位置变化情况.
新知探索
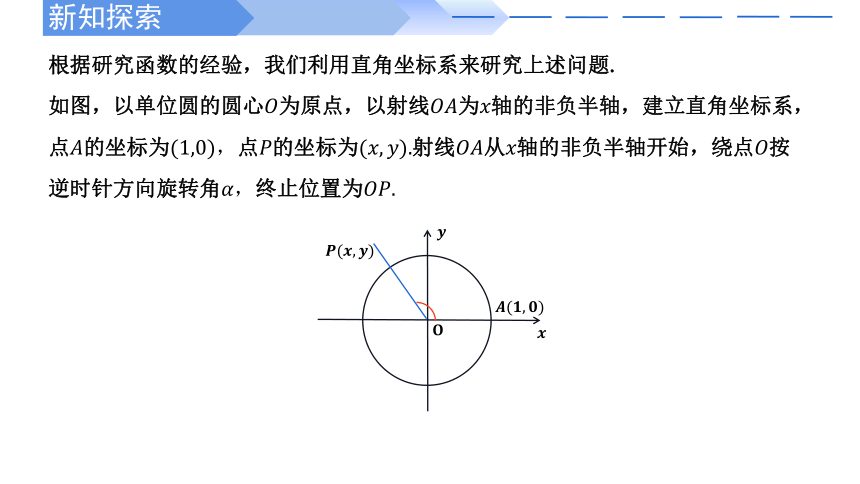
根据研究函数的经验,我们利用直角坐标系来研究上述问题.
如图,以单位圆的圆心为原点,以射线为轴的非负半轴,建立直角坐标系,点的坐标为,点的坐标为.射线从轴的非负半轴开始,绕点按逆时针方向旋转角,终止位置为.
新知探索
Q1:当时,点的坐标是什么?
Q2:当或时,点的坐标又是什么?它们是唯一确定的吗?
Q3:一般地,任意给定一个角,它的终边与单位圆交点的坐标能唯一确定吗?
利用勾股定理可以发现,当时,点的坐标是;
当时,点的坐标是和它们都是唯一确定的.
新知探索
一般地,任意给定一个角它的终边与单位圆交点的坐标,无论是横坐标还是纵坐标,都是唯一确定的.所以,点的横坐标、纵坐标都是角的函数.下面给出这些函数的定义.
设是一个任意角,,它的终边与单位圆交点.
新知探索
1.把点的纵坐标叫做的正弦函数,记作,即
2.把点的横坐标叫做的余弦函数,记作,即
3.把点的纵坐标与横坐标的比值叫做的正切,记作,即
可以看出,当时,的终边在轴上,这是点的横坐标等于0,所以无意义.除此之外,对于确定的角,的值也是唯一确定的.所以,也是以角为自变量,以单位圆上的点的纵坐标与横坐标的比值为函数值的函数,称为正切函数.
新知探索
我们将正弦函数、余弦函数和正切函数统称为三角函数,通常将它们记为:
正弦函数
余弦函数
正切函数
在初中我们学了锐角三角函数,知道它们都是以锐角为自变量,以比值为函数值的函数.设,把按锐角三角函数定义求得的锐角的正弦记为,并把按本节三角函数定义求得的的正弦记为.我们发现与是相等的,且对于余弦、正切也有相同的结论.
例析
例1.求的正弦、余弦和正切值.
解:在直角坐标系中,作易知的终边与单位圆的交点坐标为.所以有:
例析
例2.如图,设是一个任意角,它的终边上任意一点(不与原点重合)的坐标为
,点与原点的距离为.求证:
证明:如图,设角的终边与单位圆交于交点分别过点,作轴的垂线,垂足分别为则:
,,,,
于是,,即.因为与同号,所以
即同理可得,
根据勾股定理,.由例2可知,只要知道角终边上任意一点的坐标,就可以求得角的各个三角函数值,并且这些函数值不会随点的位置的改变而改变.
新知探索
学习了三角函数的定义,接下来研究它们的一些性质.
活动2:根据任意角的三角函数定义,先将正弦、余弦、正切函数在弧度制下的定义域填入下表,再将这三种函数的值在各象限的符号填入图中的括号.
三角函数 定义域
( + )
( + )
( + )
( + )
三角函数值在各象限内的符号,我们可以简记为:“一全正二正弦三正切四余弦.”
或“全STC”.(意思是在第一象限全为正,第二象限正弦为正,第三象限正切为正,第四象限余弦为正)
( + )
+
( - )
( - )
( - )
( - )
( - )
( - )
新知探索
辨析1:判断正误.
(1)已知是三角形的内角,则必有( )
(2)若,则是第一或第二象限角.( )
(3)对于任意角,都有意义.( )
答案:√,×,×.
辨析2:若则在( ).
A.第一象限 B.第二象限 C.第三象限 D.第四象限
答案:C.
例析
例3.求证:角为第三象限角的充要条件是
证明:先证充分性,即如果式都成立,那么为第三象限角.
因为式成立,所以角的终边可能位于第三或第四象限,也可能与轴的负半轴重合;
又因为式成立,所以角的终边可能位于第一或第三象限.
因为式都成立,所以角的终边只能位于第三象限.于是角为第三象限角.
必要性,即若为第三象限角,则有且成立.
新知探索
活动3:现在我们尝试从三角函数的定义出发,讨论一下什么时候三角函数取值相等?
由三角函数的定义,可以知道:终边相同的角的同一三角函数的值相等.
由此,我们可以得到一组公式:
公式一
其中
新知探索
公式一
其中
利用公式一,可以把求任意角的三角函数值,转化为求(或0°360°)角的三角函数值.
由公式一可知,三角函数值拥有“周而复始”的变化规律,即角的终边每绕原点旋转一周,函数值将重复出现.
新知探索
辨析3:判断正误.
(1)若,则( )
(2)若,则.( )
答案:√,×.
辨析4:(1)的值是________.
(2)________.
答案:(1);(2).
例析
例4.确定下列三角函数值的符号,然后用计算工具验证:
(1)(2);(3);(4)
解:(1)因为是第三象限角,所以;
(2)因为是第四象限角,所以
(3)因为
而是第一象限角,所以>0.
(4)因为而的终边在轴上,
所以
例析
例5.求下列三角函数值:
(1)(精确到0.001);(2);(3)
解:(1);
(2)
(3).
练习
例1.已知角的终边上有一点,且,求的值.
题型一:三角函数的定义与应用
解:∵∴
又,∴∴又
∴是第一或第二象限角.
当是第一象限角时,则.
当是第二象限角时,则.
练习
变1.已知角的终边落在直线上,求的值.
解:直线,即经过第二、四象限.
在第二象限取直线上的点,则
∴,,
在第四象限取直线上的点
∴.
练习
利用三角函数的定义求角的三角函数值的类型:
(1)若已知角,则只需确定出该角的终边与单位圆的交点坐标,即可求出各三角函数值;
(2)若已知角终边上一点为单位圆上的点,则
(3)若已知角终边上一点不是单位圆上一点,则
(4)若已知角终边上点的坐标含参数,则需对其所在象限进行分类讨论.
练习
题型二:三角函数值符号的运用
例2.已知点位于第二象限,那么角所在的象限是( ).
A.第一象限 B.第二象限 C.第三象限 D.第四象限
答案:C.
由点位于第二象限,
可得,可得.
所以角所在的象限是第三象限.
变2.(1)若三角形的两内角满足,则此三角形必为( ).
A.锐角三角形 B.钝角三角形 C.直角三角形 D.以上三种情况都有可能
答案:B.三角形的两内角的终边一定落在第一、第二象限或轴正半轴上,
所以所以角为钝角,此三角形为钝角三角形.
练习
变2.(2)的符号为_______(填“正”或“负”).
答案:负.∵,,∴分别为第三、第二、第一象限角,∴∴的符号为负.
练习
有关三角函数值符号问题的解题策略:
(1)若已知角的三角函数值(,,)中任意两个的符号,可分别确定出角终边所在的可能位置,二者的公共部分即角的终边位置.注意终边在坐标轴上的特殊情况.
(2)对于多个三角函数值符号的判断问题,需进行分类讨论.
(3)对于确定角是第几象限角的问题,应先确定题目中所有三角函数值的符号,然后依据上述三角函数值的符号来确定角是第几象限角,它们的公共部分即为所求;对于已知角的终边所在的象限来判断角的三角函数值的符号问题,则常依据三角函数的定义,或利用口诀“一全正,二正弦,三正切,四余弦”来解决.
练习
题型三:诱导公式一的应用
例3.求值:
(1)(2).
解:(1)原式
(2)原式
.
变3.求下列各式的值:
(1)(2).
解:(1)原式
(2)原式
练习
练习
利用诱导公式一进行求值化简的步骤:
定形
转化
求值
将已知的任意角写成的形式,其中
根据诱导公式,转化为角的某个三角函数值
若角为特殊角,可直接求出该角的三角函数值
课堂小结&作业
课堂小结:
(1)任意角的三角函数的定义;
(2)三角函数值的符号;
(3)诱导公式一.
作业:
(1)整理本节课的题型;
(2)课本P182的练习15题.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
