冀教版九年级数学上册 第26章解直角三角形 单元测试卷(word版无答案)
文档属性
| 名称 | 冀教版九年级数学上册 第26章解直角三角形 单元测试卷(word版无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 316.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-24 11:33:02 | ||
图片预览

文档简介
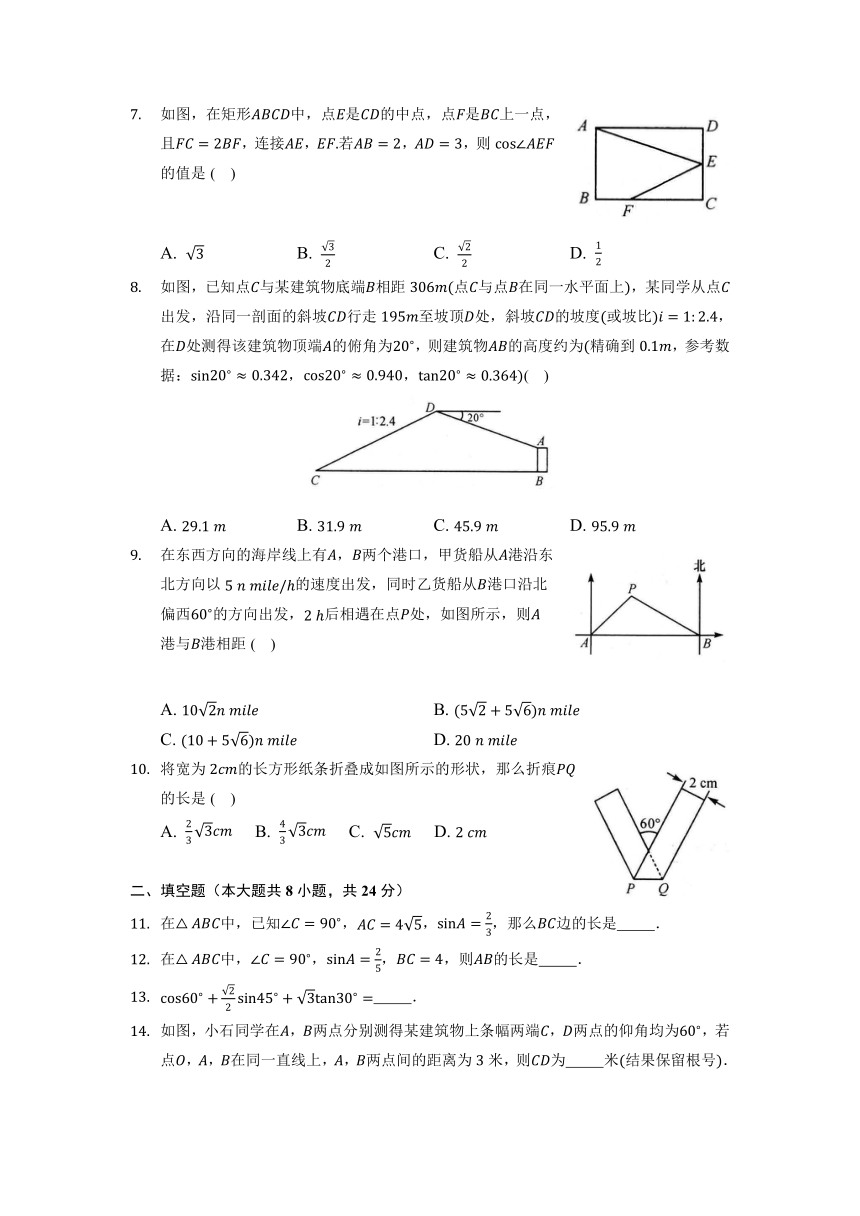
第26章 解直角三角形 单元测试卷
一、选择题(本大题共10小题,共30分。在每小题列出的选项中,选出符合题目的一项)
在中,,,那么的长是( )
A. B. C. D.
如图,在中,,,则的值是( )
A. B. C. D.
如图,点,,在正方形网格的格点上,则( )
A. B. C. D.
如图,点,,在正方形网格的格点上,则( )
A. B. C. D.
在中,,若,,则斜边上的高等于( )
A. B. C. D.
如图,在中,,于点,则下列结论不正确的是( )
A. B. C. D.
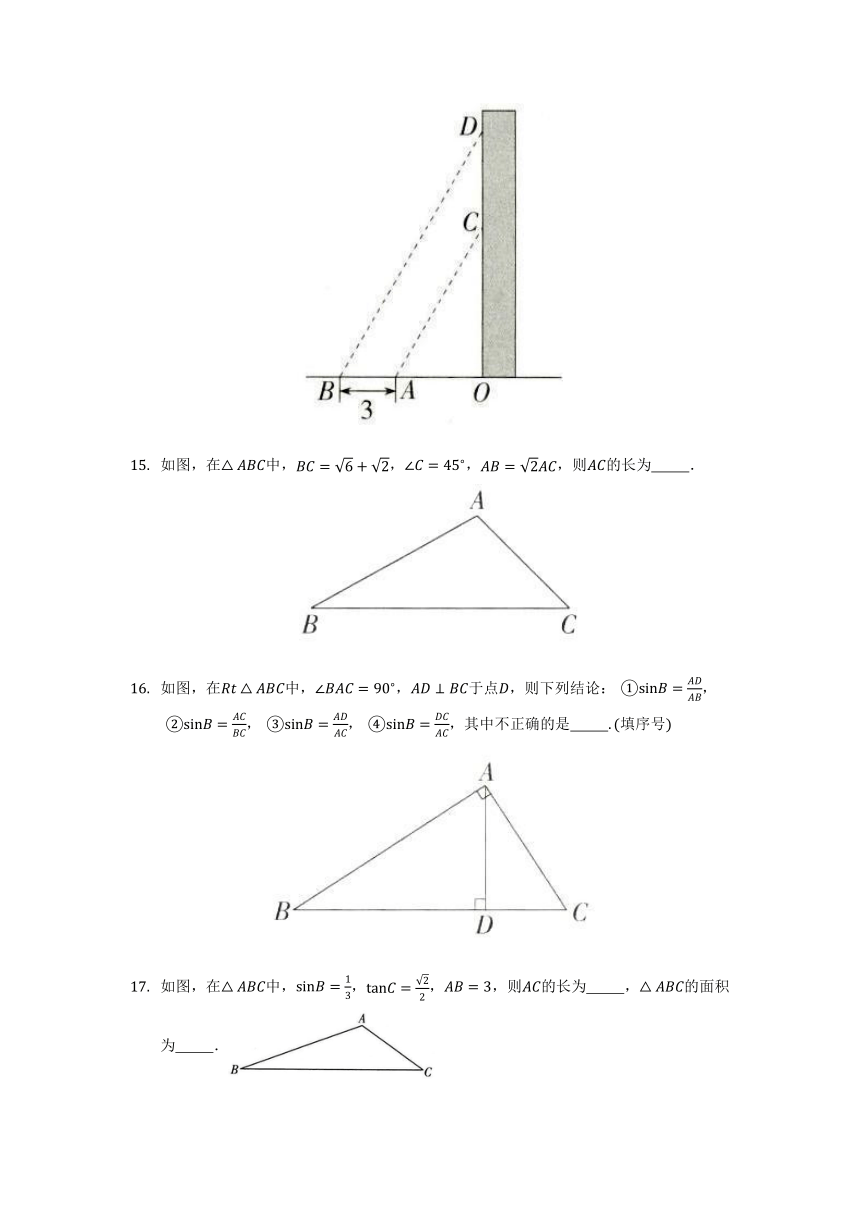
如图,在矩形中,点是的中点,点是上一点,且,连接,若,,则的值是( )
A. B. C. D.
如图,已知点与某建筑物底端相距点与点在同一水平面上,某同学从点出发,沿同一剖面的斜坡行走至坡顶处,斜坡的坡度或坡比,在处测得该建筑物顶端的俯角为,则建筑物的高度约为精确到,参考数据:,,( )
A. B. C. D.
在东西方向的海岸线上有,两个港口,甲货船从港沿东北方向以的速度出发,同时乙货船从港口沿北偏西的方向出发,后相遇在点处,如图所示,则港与港相距( )
A. B.
C. D.
将宽为的长方形纸条折叠成如图所示的形状,那么折痕的长是( )
A. B. C. D.
二、填空题(本大题共8小题,共24分)
在中,已知,,,那么边的长是 .
在中,,,,则的长是 .
.
如图,小石同学在,两点分别测得某建筑物上条幅两端,两点的仰角均为,若点,,在同一直线上,,两点间的距离为米,则为 米结果保留根号.
如图,在中,,,,则的长为 .
如图,在中,,于点,则下列结论:,,,,其中不正确的是 填序号
如图,在中,,,,则的长为 ,的面积为 .
如图,建筑物的高为,在其楼顶测得旗杆底部的俯角为,旗杆顶部的仰角为,则旗杆的高度约为 结果精确到,参考数据:,,
三、解答题(本大题共8小题,共66分。解答应写出文字说明,证明过程或演算步骤)
已知:在中,,,,求的周长和面积.
一艘船向东航行,上午时到达一座灯塔的西南海里的处,中午时到达这座灯塔的正南处,求这艘船航行的速度结果精确到海里时.
在等腰三角形中,,,求,,的值.
如图,小莹在数学综合实践活动中,利用所学的数学知识对某小区居民楼的高度进行测量先测得居民楼与之间的距离为,后站在点处测得居民楼的顶端的仰角为,居民楼的顶端的仰角为已知居民楼的高度为,小莹的观测点距地面求居民楼的高度结果精确到,参考数据:,,.
速滑运动受到许多年轻人的喜爱如图,四边形是某速滑场馆建造的滑台,已知,滑台的高为米,且坡面的坡度为后来为了提高安全性,决定降低坡度,改造后的新坡面的坡度为.
求新坡面的坡角及的长
原坡面底部的正前方米处即米是护墙,为保证安全,体育管理部门规定,坡面底部至少距护墙米请问:新的设计方案能否通过试说明理由参考数据:
某条道路上通行车辆限速为千米时,在离道路米的点处建一个监测点,道路段为检测区如图在中,已知,,那么车辆通过段的时间在多少秒以内时,可认定为超速精确到秒,参考数据:,,
阅读以下材料,并按要求完成相应的任务构建几何图形解决代数问题是“数形结合”思想的重要应用,例如在计算时,可构造如图所示的图形,在中,,,,易得,,延长至点,使得,连接,易知,,所以
任务:
请根据上面的步骤,完成的计算
类比这种方法,画出图形,并计算的值.
如图,公路为东西走向,在点北偏东方向上,距离千米处是村庄在点北偏东方向上,距离千米处是村庄.
求,两村之间的距离.
要在公路旁修建一个土特产收购站,使得,两村到站的距离之和最短,求这个最短距离之和.
参考数据:,,
一、选择题(本大题共10小题,共30分。在每小题列出的选项中,选出符合题目的一项)
在中,,,那么的长是( )
A. B. C. D.
如图,在中,,,则的值是( )
A. B. C. D.
如图,点,,在正方形网格的格点上,则( )
A. B. C. D.
如图,点,,在正方形网格的格点上,则( )
A. B. C. D.
在中,,若,,则斜边上的高等于( )
A. B. C. D.
如图,在中,,于点,则下列结论不正确的是( )
A. B. C. D.
如图,在矩形中,点是的中点,点是上一点,且,连接,若,,则的值是( )
A. B. C. D.
如图,已知点与某建筑物底端相距点与点在同一水平面上,某同学从点出发,沿同一剖面的斜坡行走至坡顶处,斜坡的坡度或坡比,在处测得该建筑物顶端的俯角为,则建筑物的高度约为精确到,参考数据:,,( )
A. B. C. D.
在东西方向的海岸线上有,两个港口,甲货船从港沿东北方向以的速度出发,同时乙货船从港口沿北偏西的方向出发,后相遇在点处,如图所示,则港与港相距( )
A. B.
C. D.
将宽为的长方形纸条折叠成如图所示的形状,那么折痕的长是( )
A. B. C. D.
二、填空题(本大题共8小题,共24分)
在中,已知,,,那么边的长是 .
在中,,,,则的长是 .
.
如图,小石同学在,两点分别测得某建筑物上条幅两端,两点的仰角均为,若点,,在同一直线上,,两点间的距离为米,则为 米结果保留根号.
如图,在中,,,,则的长为 .
如图,在中,,于点,则下列结论:,,,,其中不正确的是 填序号
如图,在中,,,,则的长为 ,的面积为 .
如图,建筑物的高为,在其楼顶测得旗杆底部的俯角为,旗杆顶部的仰角为,则旗杆的高度约为 结果精确到,参考数据:,,
三、解答题(本大题共8小题,共66分。解答应写出文字说明,证明过程或演算步骤)
已知:在中,,,,求的周长和面积.
一艘船向东航行,上午时到达一座灯塔的西南海里的处,中午时到达这座灯塔的正南处,求这艘船航行的速度结果精确到海里时.
在等腰三角形中,,,求,,的值.
如图,小莹在数学综合实践活动中,利用所学的数学知识对某小区居民楼的高度进行测量先测得居民楼与之间的距离为,后站在点处测得居民楼的顶端的仰角为,居民楼的顶端的仰角为已知居民楼的高度为,小莹的观测点距地面求居民楼的高度结果精确到,参考数据:,,.
速滑运动受到许多年轻人的喜爱如图,四边形是某速滑场馆建造的滑台,已知,滑台的高为米,且坡面的坡度为后来为了提高安全性,决定降低坡度,改造后的新坡面的坡度为.
求新坡面的坡角及的长
原坡面底部的正前方米处即米是护墙,为保证安全,体育管理部门规定,坡面底部至少距护墙米请问:新的设计方案能否通过试说明理由参考数据:
某条道路上通行车辆限速为千米时,在离道路米的点处建一个监测点,道路段为检测区如图在中,已知,,那么车辆通过段的时间在多少秒以内时,可认定为超速精确到秒,参考数据:,,
阅读以下材料,并按要求完成相应的任务构建几何图形解决代数问题是“数形结合”思想的重要应用,例如在计算时,可构造如图所示的图形,在中,,,,易得,,延长至点,使得,连接,易知,,所以
任务:
请根据上面的步骤,完成的计算
类比这种方法,画出图形,并计算的值.
如图,公路为东西走向,在点北偏东方向上,距离千米处是村庄在点北偏东方向上,距离千米处是村庄.
求,两村之间的距离.
要在公路旁修建一个土特产收购站,使得,两村到站的距离之和最短,求这个最短距离之和.
参考数据:,,
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
