2018-2022高考真题 圆锥曲线 解答题全集(PDF版含解析)
文档属性
| 名称 | 2018-2022高考真题 圆锥曲线 解答题全集(PDF版含解析) |  | |
| 格式 | |||
| 文件大小 | 7.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-23 07:10:10 | ||
图片预览




文档简介
2018-2022高考真题圆锥曲线解答题全集(学生版解析版)
一,解答题(共60小题)
1.(202~全国)已知椭圆C的左、右焦点分别为F(~c0,户(c,0),直线)=23
交C于A,B两点,AB=2V7,四边形AF1BF2的面积为4V3.
(1)求c:
(2)求C的方程.
2.(202天津)椭圆后+兰=1o>6>0)的右焦点为R、右顶点为A,上顶点为公.且
,y2
Q2
满足EV3
ABI 2
(1)求椭圆的离心率e:
(2)直线1与椭圆有唯一公共点M,与y轴相交于N(N异于M).记O为坐标原点,
若OM=OM,且△OMN的面积为V3,求椭圆的标准方程.
3.(2022上海)设有椭圆方程r:兰+
a2+2=l(a>b>0),直线:x+y-4W2=0,下下端
点为A,M在1上,左、右焦点分别为F1(-v2,0)、F2(√2,0).
(1)a=2,AM中点在x轴上,求点M的坐标:
V了母1学第身可荡Wv
求b:
(3)在椭圆T上存在一点P到I距离为d,使PF+PF2+d=6,随a的变化,求d的最
小值
B
M
F2
·浙江)如图,已知椭圆+2=1.设A,B是椭圆上异于P(0,1D
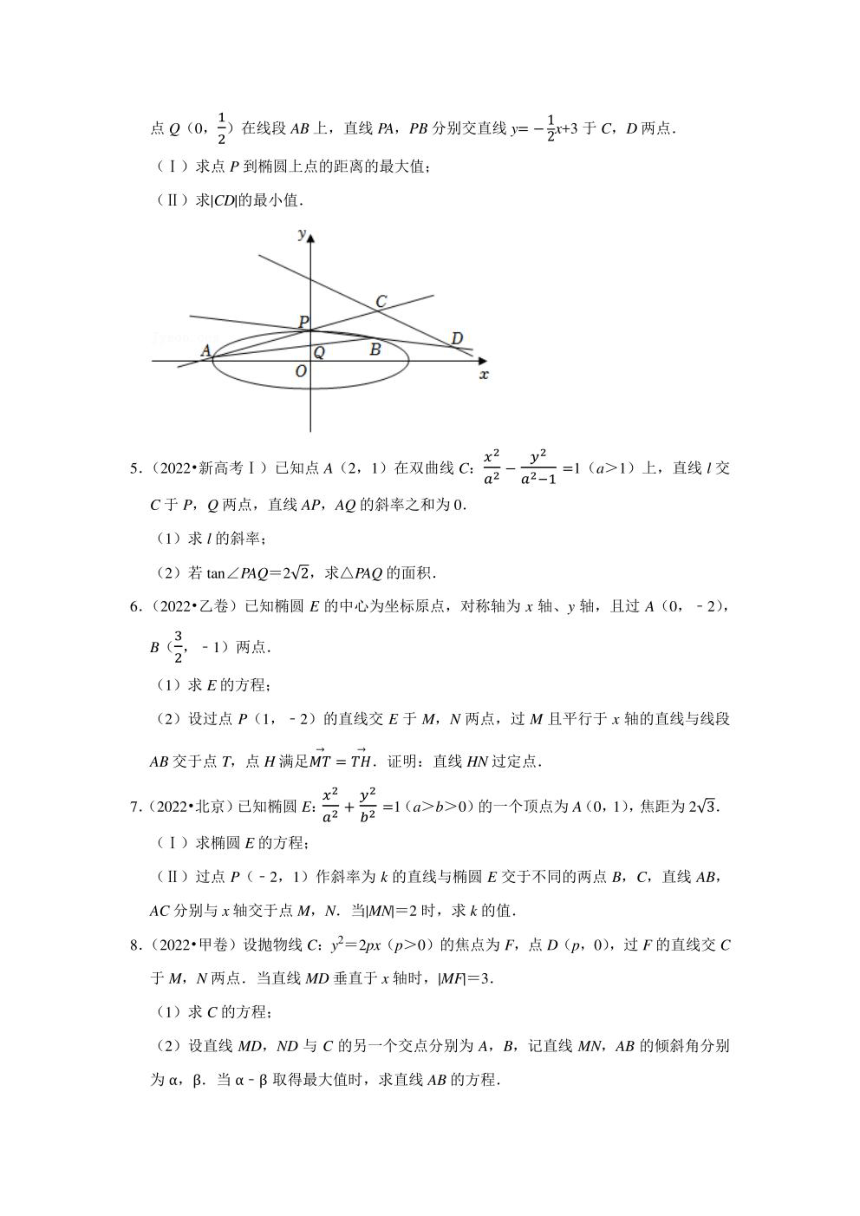
点Q(0,宝在线段AB上,直线A,PB分别交直线)=-2+3于C,D两点。
(I)求点P到椭圆上点的距离的最大值:
(Ⅱ)求1CD的最小值.
y米
D
B
522:新商考D已知点A2.D在双自线C器-二=1(o>D上,直线1交
C于P,Q两点,直线AP,AQ的斜率之和为0.
(1)求1的斜率:
(2)若tan∠PAQ=2V2,求△PAQ的面积.
6.(2022·乙卷)已知椭圆E的中心为坐标原点,对称轴为x轴、y轴,且过A(0,-2),
,-1)两点.
(1)求E的方程:
(2)设过点P(1,-2)的直线交E于M,N两点,过M且平行于x轴的直线与线段
AB交于点T,点H满足MT=TH.证明:直线HN过定点
x2.y2
7.(2022北京)已知椭圆E:三+京=1(a>b>0)的-个顶点为A(0,1D,焦距为2V3.
(I)求椭圆E的方程:
(Ⅱ)过点P(-2,1)作斜率为k的直线与椭圆E交于不同的两点B,C,直线AB,
AC分别与x轴交于点M,N.当IMW=2时,求k的值.
8.(2022甲卷)设抛物线C:y2=2px(p>0)的焦点为F,点D(p,0),过F的直线交C
于M,N两点,当直线MD垂直于x轴时,MF=3.
(1)求C的方程:
(2)设直线MD,ND与C的另一个交点分别为A,B,记直线MN,AB的倾斜角分别
为a,B.当C-阝取得最大值时,求直线AB的方程.
一,解答题(共60小题)
1.(202~全国)已知椭圆C的左、右焦点分别为F(~c0,户(c,0),直线)=23
交C于A,B两点,AB=2V7,四边形AF1BF2的面积为4V3.
(1)求c:
(2)求C的方程.
2.(202天津)椭圆后+兰=1o>6>0)的右焦点为R、右顶点为A,上顶点为公.且
,y2
Q2
满足EV3
ABI 2
(1)求椭圆的离心率e:
(2)直线1与椭圆有唯一公共点M,与y轴相交于N(N异于M).记O为坐标原点,
若OM=OM,且△OMN的面积为V3,求椭圆的标准方程.
3.(2022上海)设有椭圆方程r:兰+
a2+2=l(a>b>0),直线:x+y-4W2=0,下下端
点为A,M在1上,左、右焦点分别为F1(-v2,0)、F2(√2,0).
(1)a=2,AM中点在x轴上,求点M的坐标:
V了母1学第身可荡Wv
求b:
(3)在椭圆T上存在一点P到I距离为d,使PF+PF2+d=6,随a的变化,求d的最
小值
B
M
F2
·浙江)如图,已知椭圆+2=1.设A,B是椭圆上异于P(0,1D
点Q(0,宝在线段AB上,直线A,PB分别交直线)=-2+3于C,D两点。
(I)求点P到椭圆上点的距离的最大值:
(Ⅱ)求1CD的最小值.
y米
D
B
522:新商考D已知点A2.D在双自线C器-二=1(o>D上,直线1交
C于P,Q两点,直线AP,AQ的斜率之和为0.
(1)求1的斜率:
(2)若tan∠PAQ=2V2,求△PAQ的面积.
6.(2022·乙卷)已知椭圆E的中心为坐标原点,对称轴为x轴、y轴,且过A(0,-2),
,-1)两点.
(1)求E的方程:
(2)设过点P(1,-2)的直线交E于M,N两点,过M且平行于x轴的直线与线段
AB交于点T,点H满足MT=TH.证明:直线HN过定点
x2.y2
7.(2022北京)已知椭圆E:三+京=1(a>b>0)的-个顶点为A(0,1D,焦距为2V3.
(I)求椭圆E的方程:
(Ⅱ)过点P(-2,1)作斜率为k的直线与椭圆E交于不同的两点B,C,直线AB,
AC分别与x轴交于点M,N.当IMW=2时,求k的值.
8.(2022甲卷)设抛物线C:y2=2px(p>0)的焦点为F,点D(p,0),过F的直线交C
于M,N两点,当直线MD垂直于x轴时,MF=3.
(1)求C的方程:
(2)设直线MD,ND与C的另一个交点分别为A,B,记直线MN,AB的倾斜角分别
为a,B.当C-阝取得最大值时,求直线AB的方程.
同课章节目录
