数学人教A版(2019)必修第一册4.2.1 指数函数的概念 课件(共18张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册4.2.1 指数函数的概念 课件(共18张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 31.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-23 07:20:02 | ||
图片预览





文档简介
(共18张PPT)
一、创设情境、导入新课
通过函数性质的学习和对幂函数的研究,我们掌握了研究函数的一般方法:
背景
概念
图像与性质
应用
那么这节课我们来研究一类很重要的基本初等函数——指数函数
4.2.1 指数函数的概念
【问题1】随着中国经济的高速增长,旅游人数不断增加,A、B两个景区自 2001年起采取了不同的应对措施,A地提高了门票价格,B地则取消了门票.下表给了A、B两个景区2001~2015年的游客人次及逐年增加量.
探究1 比较一下两地景区旅游人次的变化情况,你发现了怎样的规律?
A景区 B景区
年份 人次 增加量 人次 增加量
2001 600 278
2002 609 9 309 31
2003 620 11 344 35
2004 631 11 383 39
2005 641 10 427 44
2006 650 9 475 48
2007 661 11 528 53
2008 671 10 588 60
2009 681 10 655 67
2010 691 10 729 74
2011 702 11 811 82
2012 711 9 903 92
2013 721 10 1005 102
2014 732 11 1118 113
2015 743 11 1224 126
画散点图
用什么方法更易发现规律
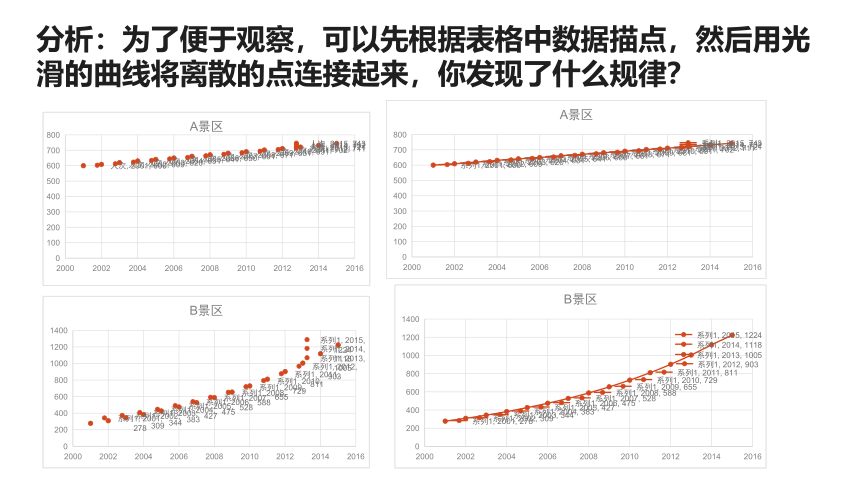
分析:为了便于观察,可以先根据表格中数据描点,然后用光滑的曲线将离散的点连接起来,你发现了什么规律?
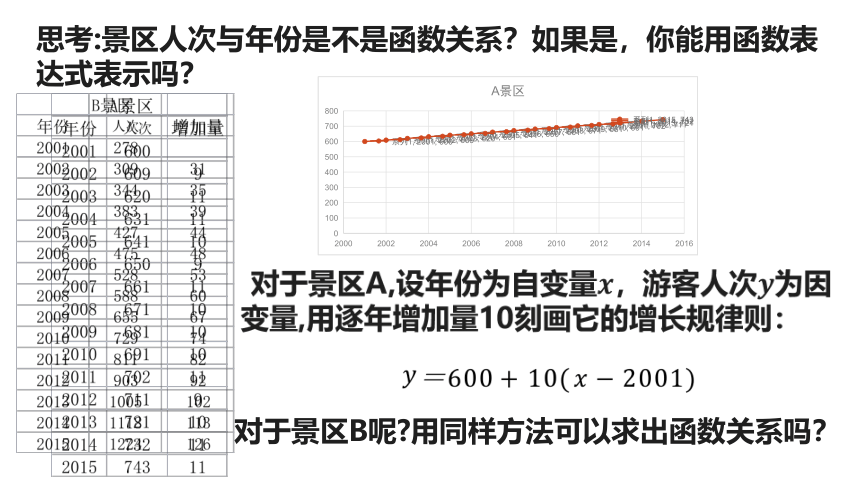
思考:景区人次与年份是不是函数关系?如果是,你能用函数表达式表示吗?
对于景区B呢 用同样方法可以求出函数关系吗?
【探究】我们知道,年增加量是对相邻两年的游客人次做减法得到的.那么能否通过对B景区每年的游客人次做其他运算来发现规律呢?
增加量=变后量-变前量
从2002年起,将B景区每年的游客人次除以上一年的游客人次,可以得到
【结论】结果表明,B景区的游客人次的年增长率都约为1.11-1=0.11,是一个常数.
……
增长率=
增加量
变前量
=
变前量
变后量-变前量
=
变前量
变后量
-1
总结:B景区的游客人次的年增长率都约为0.11.增长率为常数的变化方式,我们称为指数增长,因此,B景区的游客人次近似于指数增长.
B景区:2001年的游客人次为278万;
1年后,游客人次是2001年的1.11倍;
2年后,游客人次是2001年的1.11 ;
3年后,游客人次是2001年的1.11 ;
··· ··· ··· ···
x年后,游客人次是2001年的1.11x;
如果设x年后的游客人次是2001年的y倍,那么
y=1.11x(x∈[0,+∞)).
问题2 从2021年3月20日起,国家考古队在三星堆又有一系列重大收获,如黄金面具、青铜神树、青铜纵目面具等,震惊了世界。据考古专家推断,三星堆文物距今已有3219年!如何推断的?
【追问】 当生物死亡后,它机体内原有的碳14含量会按照确定的比率衰减(称为衰减率),大约经过5730年衰减为原来的一半,这个时间称为半衰期。按照上述变化规律,生物体内碳14与死亡年数之间有怎样的关系?
设死亡生物体内碳14含量的年衰减率为p,则
死亡1年后,生物体内碳14含量为(1-p);
死亡2年后,生物体内碳14含量为(1-p)2;……
死亡5730年后,生物体内碳14含量为(1-p)5730;
死亡x年后呢?
提炼:
问题:以上两个式子有何共同特征?
(1)均是幂形式;
(2)底是一个常数;
(3)自变量x在指数位置上;
y=1.11x
二、抽象特征,形成概念
指数函数的定义
一般地:形如y = ax (a>0且a≠1)的函数叫做指数函数.其中x是自变量,函数的定义域是R
观察指数函数的特点:
系数为1
底数为正数且不为1
x系数为1
指数函数y=ax(a>0且a≠1)与幂函数y=xa有什么区别和联系?
0
1
a
当a=1时,a x 恒等于1,没有研究的必要.
当a<0时,a x有些会没有意义,如
当a=0时,a x有些会没有意义,如
为了便于研究,规定: (a>0且a≠1)
为什么概念中明确规定a>0,且 a≠1?
三、概念应用,加深理解
例1 已知指数函数f(x)=ax (a>0,且a≠1) ,且f(3)=π,求f(0),f(1),f(-3)的值.
例2(1)设经过年后,游客给A、B两地带来的收入分别为
f(x),g(x)。对于A景区:2001年600万,年后,游客人次的增长规律则:
B景区:2001年的游客人次为278万;如果设x年后的游客人次是2001年的y倍,那么
y=1.11x(x∈[0,+∞)).
y=10x+600(x∈[0,+∞))
(x∈[0,+∞))
(x∈[0,+∞))
例2(2)设生物死亡年数为x,死亡生物体内碳14含量为
当x=1000时,
所以,生物死亡1000年以后,它体内碳14含量缩减为原来的约30%。
小结:
1、我们是如何引出指数函数概念的?
四、课堂总结,提炼升华
2、么样的函数是指数函数,其解析式有什么特征?
实际问题
数学问题
指数函数的概念
抽象
归纳
(a>0且a≠1)
习题4.2 第2、4、8题
四、布置作业
一、创设情境、导入新课
通过函数性质的学习和对幂函数的研究,我们掌握了研究函数的一般方法:
背景
概念
图像与性质
应用
那么这节课我们来研究一类很重要的基本初等函数——指数函数
4.2.1 指数函数的概念
【问题1】随着中国经济的高速增长,旅游人数不断增加,A、B两个景区自 2001年起采取了不同的应对措施,A地提高了门票价格,B地则取消了门票.下表给了A、B两个景区2001~2015年的游客人次及逐年增加量.
探究1 比较一下两地景区旅游人次的变化情况,你发现了怎样的规律?
A景区 B景区
年份 人次 增加量 人次 增加量
2001 600 278
2002 609 9 309 31
2003 620 11 344 35
2004 631 11 383 39
2005 641 10 427 44
2006 650 9 475 48
2007 661 11 528 53
2008 671 10 588 60
2009 681 10 655 67
2010 691 10 729 74
2011 702 11 811 82
2012 711 9 903 92
2013 721 10 1005 102
2014 732 11 1118 113
2015 743 11 1224 126
画散点图
用什么方法更易发现规律
分析:为了便于观察,可以先根据表格中数据描点,然后用光滑的曲线将离散的点连接起来,你发现了什么规律?
思考:景区人次与年份是不是函数关系?如果是,你能用函数表达式表示吗?
对于景区B呢 用同样方法可以求出函数关系吗?
【探究】我们知道,年增加量是对相邻两年的游客人次做减法得到的.那么能否通过对B景区每年的游客人次做其他运算来发现规律呢?
增加量=变后量-变前量
从2002年起,将B景区每年的游客人次除以上一年的游客人次,可以得到
【结论】结果表明,B景区的游客人次的年增长率都约为1.11-1=0.11,是一个常数.
……
增长率=
增加量
变前量
=
变前量
变后量-变前量
=
变前量
变后量
-1
总结:B景区的游客人次的年增长率都约为0.11.增长率为常数的变化方式,我们称为指数增长,因此,B景区的游客人次近似于指数增长.
B景区:2001年的游客人次为278万;
1年后,游客人次是2001年的1.11倍;
2年后,游客人次是2001年的1.11 ;
3年后,游客人次是2001年的1.11 ;
··· ··· ··· ···
x年后,游客人次是2001年的1.11x;
如果设x年后的游客人次是2001年的y倍,那么
y=1.11x(x∈[0,+∞)).
问题2 从2021年3月20日起,国家考古队在三星堆又有一系列重大收获,如黄金面具、青铜神树、青铜纵目面具等,震惊了世界。据考古专家推断,三星堆文物距今已有3219年!如何推断的?
【追问】 当生物死亡后,它机体内原有的碳14含量会按照确定的比率衰减(称为衰减率),大约经过5730年衰减为原来的一半,这个时间称为半衰期。按照上述变化规律,生物体内碳14与死亡年数之间有怎样的关系?
设死亡生物体内碳14含量的年衰减率为p,则
死亡1年后,生物体内碳14含量为(1-p);
死亡2年后,生物体内碳14含量为(1-p)2;……
死亡5730年后,生物体内碳14含量为(1-p)5730;
死亡x年后呢?
提炼:
问题:以上两个式子有何共同特征?
(1)均是幂形式;
(2)底是一个常数;
(3)自变量x在指数位置上;
y=1.11x
二、抽象特征,形成概念
指数函数的定义
一般地:形如y = ax (a>0且a≠1)的函数叫做指数函数.其中x是自变量,函数的定义域是R
观察指数函数的特点:
系数为1
底数为正数且不为1
x系数为1
指数函数y=ax(a>0且a≠1)与幂函数y=xa有什么区别和联系?
0
1
a
当a=1时,a x 恒等于1,没有研究的必要.
当a<0时,a x有些会没有意义,如
当a=0时,a x有些会没有意义,如
为了便于研究,规定: (a>0且a≠1)
为什么概念中明确规定a>0,且 a≠1?
三、概念应用,加深理解
例1 已知指数函数f(x)=ax (a>0,且a≠1) ,且f(3)=π,求f(0),f(1),f(-3)的值.
例2(1)设经过年后,游客给A、B两地带来的收入分别为
f(x),g(x)。对于A景区:2001年600万,年后,游客人次的增长规律则:
B景区:2001年的游客人次为278万;如果设x年后的游客人次是2001年的y倍,那么
y=1.11x(x∈[0,+∞)).
y=10x+600(x∈[0,+∞))
(x∈[0,+∞))
(x∈[0,+∞))
例2(2)设生物死亡年数为x,死亡生物体内碳14含量为
当x=1000时,
所以,生物死亡1000年以后,它体内碳14含量缩减为原来的约30%。
小结:
1、我们是如何引出指数函数概念的?
四、课堂总结,提炼升华
2、么样的函数是指数函数,其解析式有什么特征?
实际问题
数学问题
指数函数的概念
抽象
归纳
(a>0且a≠1)
习题4.2 第2、4、8题
四、布置作业
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
