12.2 三角形全等的判定(4)学案
文档属性
| 名称 | 12.2 三角形全等的判定(4)学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 119.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-09-18 14:54:36 | ||
图片预览


文档简介
12.2 三角形全等的判定(4)
【学习目标】:
1、理解直角三角形全等的判定方法“HL”,并能灵活选择方法判定三角形全等;
2.通过独立思考、小组合作、展示质疑,体会探索数学结论的过程,发展合情推理能力.
【学习重点】:运用直角三角形全等的条件解决一些实际问题.
【学习难点】:熟练运用直角三角形等的条件解决一些实际问题.
【课前自学、课中交流】
一、复习准备
1、(1)判定两个三角形全等的方法: 、 、 、 .
(2)如图,Rt△ABC中,直角边是 、 ,斜边是 .
(3)如图,AB⊥BE于B,DE⊥BE于E,
①若∠A=∠D,AB=DE,
则△ABC与△DEF (填“全等”或“不全等” )根据 (用简写法)
②若∠A=∠D,BC=EF,
则△ABC与△DEF (填“全等”或“不全等” )根据 (用简写法)
③若AB=DE,BC=EF,
则△ABC与△DEF (填“全等”或“不全等” )根据 (用简写法)
④若AB=DE,BC=EF,AC=DF
则△ABC与△DEF (填“全等”或“不全等” )根据 (用简写法)
2、如果两个直角三角形满足斜边和一条直角边对应相等,这两个直角三角形全等吗?
二、探究新知
1.已知一个直角三角形的斜边和直角边,如何画出这个直角三角形?这样的两个直角三角形全等吗
2.(1)动手试一试:
已知:Rt△ABC ,∠C=90°
求作:Rt△, 使∠=90°, =AB, =BC.
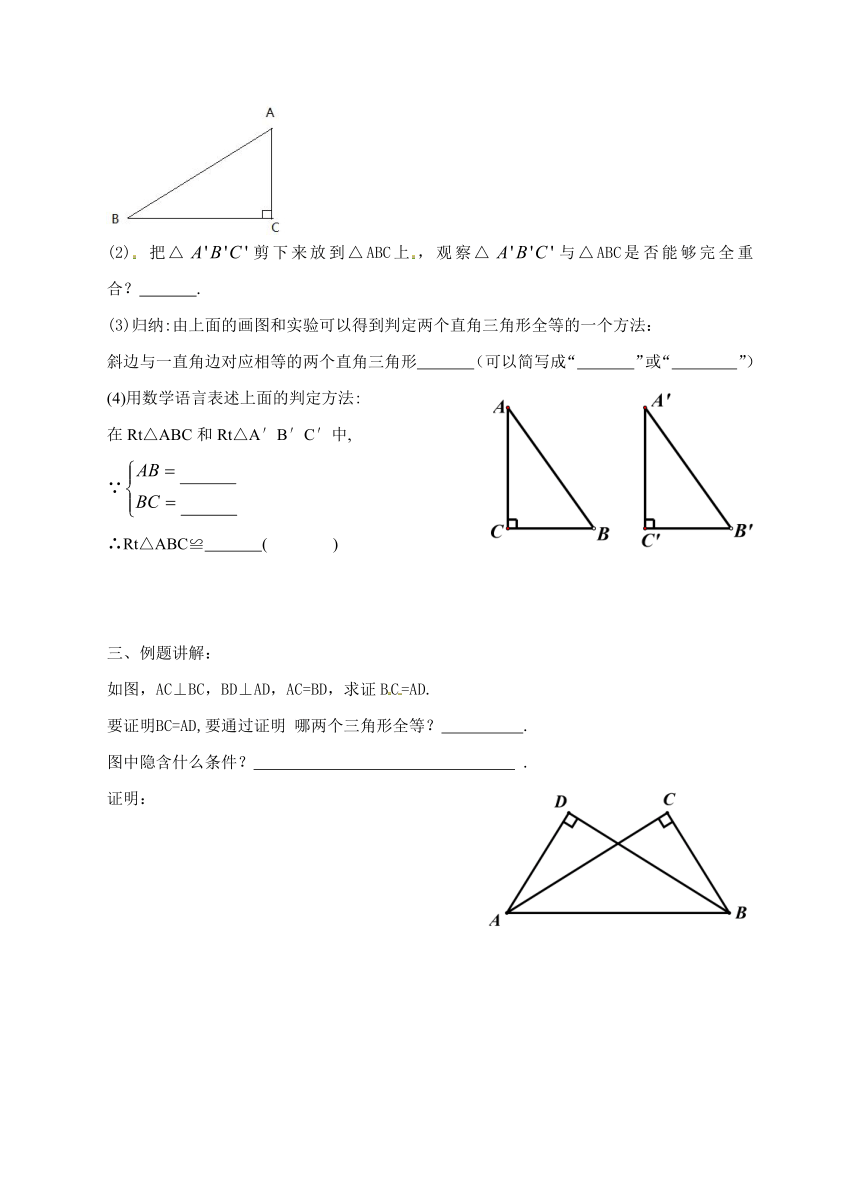
(2) 把△剪下来放到△ABC上,观察△与△ABC是否能够完全重合? .
(3)归纳:由上面的画图和实验可以得到判定两个直角三角形全等的一个方法:
斜边与一直角边对应相等的两个直角三角形 (可以简写成“ ”或“ ”)
(4)用数学语言表述上面的判定方法:
在Rt△ABC和Rt△A′B′C′中,
∵
∴Rt△ABC≌ ( )
三、例题讲解:
如图,AC⊥BC,BD⊥AD,AC=BD,求证BC=AD.
要证明BC=AD,要通过证明 哪两个三角形全等? .
图中隐含什么条件? .
证明:
【当堂训练】
1.判定两个三角形全等的方法: 、 、 、 、 .
2.判断两个直角三角形全等的方法不正确的是( )
A、两条直角边对应相等 B、斜边和一锐角对应相等
C、斜边和一条直角边对应相等 D、两个锐角对应相等
3.判断题:
(1)一个锐角和与锐角相邻的一直角边对应相等的两个直角三角形全等( )
(2)两边对应相等的两个直角三角形全等( )
(3)一个锐角与一边对应相等的两个直角三角形全等( )
4. 如图,CE⊥AB,DF⊥AB,垂足分别为E、F,
(1)若AC//DB,且AC=DB,则△ACE≌△BDF,根据 ;
(2)若AC//DB,且AE=BF,则△ACE≌△BDF,根据 ;
(3)若AE=BF,且CE=DF,则△ACE≌△BDF,根据 ;
(4)若AC=BD,AE=BF,CE=DF,则△ACE≌△BDF,根据 ;
(5) 若AC=BD,CE=DF(或AE=BF),则△ACE≌△BDF,根据 .
5.如图,AC=AD,∠C=∠D=90°.求证:BC=BD.
(第8题)
6.如图,C是路段AB的中点,两人从C同时出发,以相同的速度分别沿着两条直线行走,并同时到达D,E两地.DA⊥AB, EB⊥AB. D,E与路段AB的距离相等吗?为什么?
7.如图,AB=CD,AE⊥BC,DF⊥BC,CE=BF.求证AE=DF.
8.如图,B、E、F、C在同一直线上,AF⊥BC于F,DE⊥BC于E,AB=DC,BE=CF,你认为AB平行于CD吗?
说说你的理由.
9. 已知:如图,∠ABC=∠DCE=90°,AC=DE ,AB=CE.求证:AC⊥DE.
10.已知:如图,△ABC中,AD是它的角平分线,且BD=CD,DE、DF分别垂直于AB、AC,垂足为E、F.求证:EB=FC.
【当堂训练】答案:
1.SSS,SAS,ASA,AAS,HL.
2.D.
3.√;√;√.
4. (1)AAS;(2)ASA;(3)SAS;(4)SSS;(5)HL.
5. 证明:在Rt△ABD和Rt△ABC中,
∵
∴Rt△ABD≌Rt△ABC(HL).
∴BC=BD.
6. AD=BE.
证明:在Rt△ACD和Rt△BCE中,
∵
∴Rt△ACD≌Rt△BCE(HL).
∴AD=BE.
7. 证明:∵AE⊥BC,DF⊥BC,
∴∠AEB=∠CFD=90°.
∵CE=BF,
∴CF=BE.
在Rt△FCD和Rt△EBA中,
∵
∴Rt△FCD≌Rt△EBA(HL).
∴AE=DF.
8.AB∥CD.
证明:∵DE⊥BC,AF⊥BC,
∴∠AFB=∠CED=90°.
∵CF=BE,
∴CE=BF.
在Rt△ECD和Rt△FBA中,
∵
∴Rt△ECD≌Rt△FBA(HL).
∴∠B=∠C.
∴AB∥CD.
9. 证明:在Rt△ABC和Rt△ECD中,
∵
∴Rt△ABC≌Rt△ECD(HL).
∴∠ACB=∠D.
∵∠ACB+∠DCF=90°,
∴∠D+∠DCF=90°,
∴∠DFC=90°,
∴AC⊥DE.
10.证明:∵AD是△ABC的角平分线,
∴∠BAD=∠CAD.
∵DE、DF分别垂直于AB、AC,
∴∠AED=∠AFD=90°.
在Rt△AED和Rt△AFD中,
∵
∴Rt△AED≌Rt△AFD(AAS).
∴ED=FD.
在Rt△EBD和Rt△FCD中,
∵
∴Rt△EBD≌Rt△FCD(HL).
∴BE=FC.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
【学习目标】:
1、理解直角三角形全等的判定方法“HL”,并能灵活选择方法判定三角形全等;
2.通过独立思考、小组合作、展示质疑,体会探索数学结论的过程,发展合情推理能力.
【学习重点】:运用直角三角形全等的条件解决一些实际问题.
【学习难点】:熟练运用直角三角形等的条件解决一些实际问题.
【课前自学、课中交流】
一、复习准备
1、(1)判定两个三角形全等的方法: 、 、 、 .
(2)如图,Rt△ABC中,直角边是 、 ,斜边是 .
(3)如图,AB⊥BE于B,DE⊥BE于E,
①若∠A=∠D,AB=DE,
则△ABC与△DEF (填“全等”或“不全等” )根据 (用简写法)
②若∠A=∠D,BC=EF,
则△ABC与△DEF (填“全等”或“不全等” )根据 (用简写法)
③若AB=DE,BC=EF,
则△ABC与△DEF (填“全等”或“不全等” )根据 (用简写法)
④若AB=DE,BC=EF,AC=DF
则△ABC与△DEF (填“全等”或“不全等” )根据 (用简写法)
2、如果两个直角三角形满足斜边和一条直角边对应相等,这两个直角三角形全等吗?
二、探究新知
1.已知一个直角三角形的斜边和直角边,如何画出这个直角三角形?这样的两个直角三角形全等吗
2.(1)动手试一试:
已知:Rt△ABC ,∠C=90°
求作:Rt△, 使∠=90°, =AB, =BC.
(2) 把△剪下来放到△ABC上,观察△与△ABC是否能够完全重合? .
(3)归纳:由上面的画图和实验可以得到判定两个直角三角形全等的一个方法:
斜边与一直角边对应相等的两个直角三角形 (可以简写成“ ”或“ ”)
(4)用数学语言表述上面的判定方法:
在Rt△ABC和Rt△A′B′C′中,
∵
∴Rt△ABC≌ ( )
三、例题讲解:
如图,AC⊥BC,BD⊥AD,AC=BD,求证BC=AD.
要证明BC=AD,要通过证明 哪两个三角形全等? .
图中隐含什么条件? .
证明:
【当堂训练】
1.判定两个三角形全等的方法: 、 、 、 、 .
2.判断两个直角三角形全等的方法不正确的是( )
A、两条直角边对应相等 B、斜边和一锐角对应相等
C、斜边和一条直角边对应相等 D、两个锐角对应相等
3.判断题:
(1)一个锐角和与锐角相邻的一直角边对应相等的两个直角三角形全等( )
(2)两边对应相等的两个直角三角形全等( )
(3)一个锐角与一边对应相等的两个直角三角形全等( )
4. 如图,CE⊥AB,DF⊥AB,垂足分别为E、F,
(1)若AC//DB,且AC=DB,则△ACE≌△BDF,根据 ;
(2)若AC//DB,且AE=BF,则△ACE≌△BDF,根据 ;
(3)若AE=BF,且CE=DF,则△ACE≌△BDF,根据 ;
(4)若AC=BD,AE=BF,CE=DF,则△ACE≌△BDF,根据 ;
(5) 若AC=BD,CE=DF(或AE=BF),则△ACE≌△BDF,根据 .
5.如图,AC=AD,∠C=∠D=90°.求证:BC=BD.
(第8题)
6.如图,C是路段AB的中点,两人从C同时出发,以相同的速度分别沿着两条直线行走,并同时到达D,E两地.DA⊥AB, EB⊥AB. D,E与路段AB的距离相等吗?为什么?
7.如图,AB=CD,AE⊥BC,DF⊥BC,CE=BF.求证AE=DF.
8.如图,B、E、F、C在同一直线上,AF⊥BC于F,DE⊥BC于E,AB=DC,BE=CF,你认为AB平行于CD吗?
说说你的理由.
9. 已知:如图,∠ABC=∠DCE=90°,AC=DE ,AB=CE.求证:AC⊥DE.
10.已知:如图,△ABC中,AD是它的角平分线,且BD=CD,DE、DF分别垂直于AB、AC,垂足为E、F.求证:EB=FC.
【当堂训练】答案:
1.SSS,SAS,ASA,AAS,HL.
2.D.
3.√;√;√.
4. (1)AAS;(2)ASA;(3)SAS;(4)SSS;(5)HL.
5. 证明:在Rt△ABD和Rt△ABC中,
∵
∴Rt△ABD≌Rt△ABC(HL).
∴BC=BD.
6. AD=BE.
证明:在Rt△ACD和Rt△BCE中,
∵
∴Rt△ACD≌Rt△BCE(HL).
∴AD=BE.
7. 证明:∵AE⊥BC,DF⊥BC,
∴∠AEB=∠CFD=90°.
∵CE=BF,
∴CF=BE.
在Rt△FCD和Rt△EBA中,
∵
∴Rt△FCD≌Rt△EBA(HL).
∴AE=DF.
8.AB∥CD.
证明:∵DE⊥BC,AF⊥BC,
∴∠AFB=∠CED=90°.
∵CF=BE,
∴CE=BF.
在Rt△ECD和Rt△FBA中,
∵
∴Rt△ECD≌Rt△FBA(HL).
∴∠B=∠C.
∴AB∥CD.
9. 证明:在Rt△ABC和Rt△ECD中,
∵
∴Rt△ABC≌Rt△ECD(HL).
∴∠ACB=∠D.
∵∠ACB+∠DCF=90°,
∴∠D+∠DCF=90°,
∴∠DFC=90°,
∴AC⊥DE.
10.证明:∵AD是△ABC的角平分线,
∴∠BAD=∠CAD.
∵DE、DF分别垂直于AB、AC,
∴∠AED=∠AFD=90°.
在Rt△AED和Rt△AFD中,
∵
∴Rt△AED≌Rt△AFD(AAS).
∴ED=FD.
在Rt△EBD和Rt△FCD中,
∵
∴Rt△EBD≌Rt△FCD(HL).
∴BE=FC.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
