2022-2023学年苏科版八年级上学期开学考试数学试卷(盐城地区)(word版 含解析)
文档属性
| 名称 | 2022-2023学年苏科版八年级上学期开学考试数学试卷(盐城地区)(word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 354.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-24 14:32:22 | ||
图片预览




文档简介
2022-2023学年苏科版八年级上学期开学考试数学试卷(盐城地区)
(时间:90分钟 满分:120分)
一.选择题(每小题3分 共30分)
1.第24届冬季奥林匹克运动会于2022年02月04日~2022年02月20日在中华人民共和国北京市和张家口市联合举行.在会徽的图案设计中,设计者常常利用对称性进行设计,下列四个图案是历届会徽图案上的一部份图形,其中不是轴对称图形的是( )
A.B. C.D.
第1题图 第3题图
2.在下列各组条件中,不能说明△ABC≌△DEF的是( )
A.AB=DE,∠B=∠E,∠C=∠F B.AC=DF,BC=EF,∠A=∠D
C.AB=DE,∠A=∠D,∠B=∠E D.AB=DE,BC=EF,AC=DF
3.如图,在△ABC中,AB=AC,D、E两点分别在AC、BC上,BD是∠ABC的平分线,DE∥AB,若BE=5cm,CE=3cm,则△CDE的周长是( )
A.15cm B.13cm C.11cm D.9cm
4.下列各式从左到右的变形属于因式分解的是 ( )
A.a(x+y) =ax+ay B.10x2-5x=5x(2x-1)
C.x2-4x+4=x(x-4+) D.x2-16+3x=(x-4)(x+4)+3x
5.下列运算中,计算结果正确的是( ).
A. B. C. D.
6.如图,根据图形的面积,可以验证一个乘法公式,这个公式是( )A. B. C. D.
7.以下图形中对称轴的数量小于3的是( )
A. B. C. D.
第7题图 第8题图
8.如图,∠C=∠D=90°,AC=AD,那么△ABC与△ABD全等的理由是( )
A.HL B.SAS C.ASA D.AAS
9.如图,在△ABC中,AC的垂直平分线分别交AB、AC于点D、E,EC=5,△ABC的周长为26,则△BDC的周长为( )
A.14 B.16 C.18 D.19
第9题图 第10题图 第11题图 第12题图
10.如图,在2×3的正方形网络中,有一个以格点为顶点的三角形,此网格中所有与该三角形成轴对称且以格点为顶点的三角形共有( )
A.1个 B.2个 C.3个 D.4个
二.题空题(每小题3分 共30分)
11.如图,在Rt△ABC 中,∠C=90°,沿过点A的一条直线AE折叠Rt△ABC,使点C恰好落在AB边的中点D处,则∠B的度数是_______
12.如图,已知AB=2,BF=8,BC=AE=6,CE=CF=7,则△CDF与四边形ABDE的面积比值是_______
13.分解因式:= .
14.若,,则 = .
15.若等腰三角形的两边的边长分别为10cm和5cm,则第三边的长是 cm.
16.如图,AB=AC,点D,E分别在AB,AC上,CD,BE交于点F,只添加一个条件使△ABE≌△ACD,添加的条件是: .
第16题图 第17题图 第18题图 第19题图 第20题图
17.如图,在△ABC中,AB=AC.以点C为圆心,以CB长为半径作圆弧,交AC的延长线于点D,连结BD.若∠A=32°,则∠CDB的大小为 度.
18.如图,在△ABC中,∠ACB=90°,D是AB边的中点若AB=18,则CD的长为 .
19.把一个长方形纸片按如图所示折叠,若量得∠AOD′=36°,则∠D′OE的度数为 .
20.如图,在△ABC中,∠ACB=90°,∠A=30°,AB=5,点P是AC上的动点,连接BP,以BP为边作等边△BPQ,连接CQ,则点P在运动过程中,线段CQ长度的最小值是 .
三.解答题(60分)
21.(12分)计算:
(1); (2) ;
(3); (4).
22.(6分)先化简,再求值:,其中a=2,b=1.
23.(6分)如图,点E在线段AC上,BC∥DE,AC=DE,CB=CE,求证:∠A=∠D.
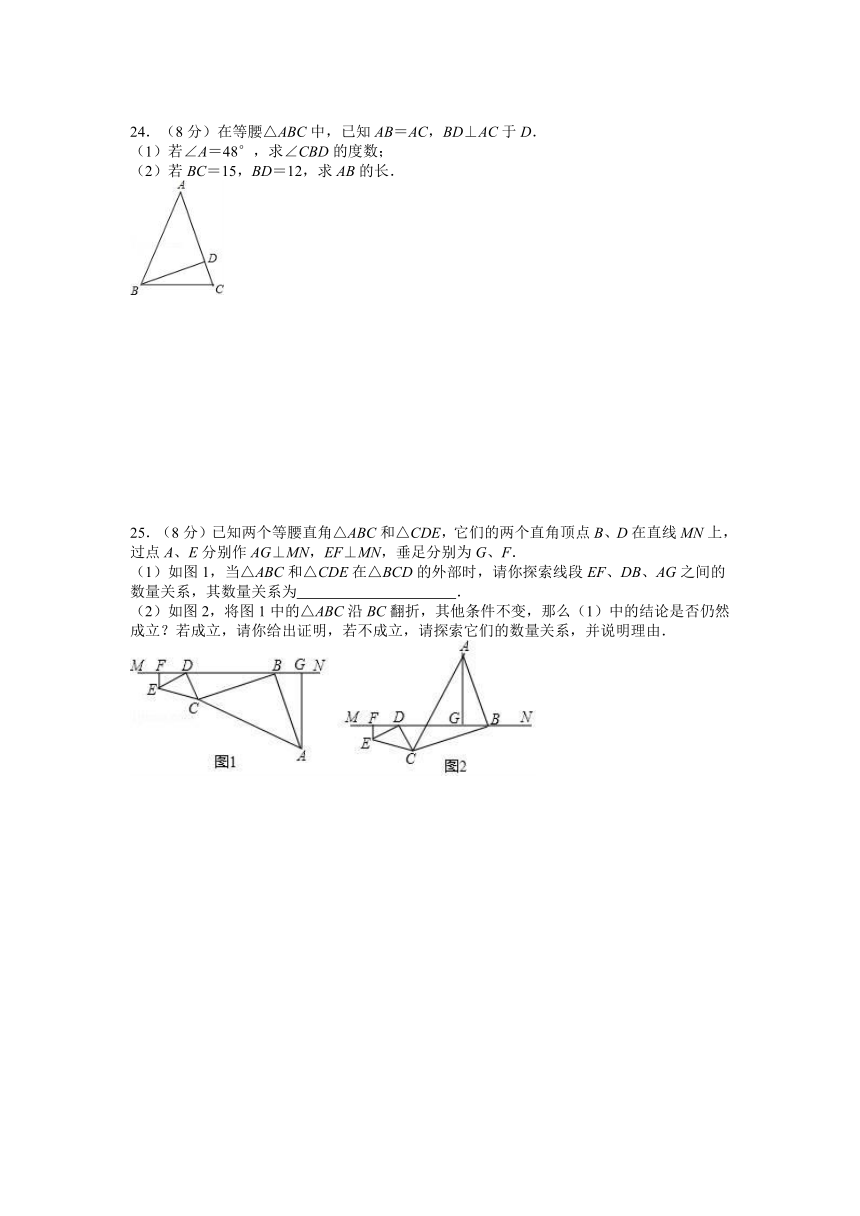
24.(8分)在等腰△ABC中,已知AB=AC,BD⊥AC于D.
(1)若∠A=48°,求∠CBD的度数;
(2)若BC=15,BD=12,求AB的长.
25.(8分)已知两个等腰直角△ABC和△CDE,它们的两个直角顶点B、D在直线MN上,过点A、E分别作AG⊥MN,EF⊥MN,垂足分别为G、F.
(1)如图1,当△ABC和△CDE在△BCD的外部时,请你探索线段EF、DB、AG之间的数量关系,其数量关系为 .
(2)如图2,将图1中的△ABC沿BC翻折,其他条件不变,那么(1)中的结论是否仍然成立?若成立,请你给出证明,若不成立,请探索它们的数量关系,并说明理由.
26.(10分)画图计算:
(1)已知△ABC,请用尺规在图1中△ABC内确定一个点P,使得点P到AB和BC的距离相等,且满足P到点B和点C的距离相等(不写作法,保留作图痕迹).
(2)如图2,如果点P是(1)中求作的点,点E、F分别在边AB、BC上,且PE=PF.
①若∠ABC=60°,求∠EPF的度数;
②若BE=2,BF=8,EP=5,求BP的长.
如图3,如果点P是△ABC内一点,且点P到点B的距离是7,若∠ABC=45°,请分别在AB、BC上求作两个点M、N,使得△PMN的周长最小(不写作法,保留作图痕迹),则△PMN的最小值为
(10分)【定义】数学课上,陈老师对我们说,如果1条线段将一个三角形分成2个等腰三角形,那么这1条线段就称为这个三角形的“好线”,如果2条线段将一个三角形分成3个等腰三角形,那么这2条线段就称为这个三角形的“好好线”.
【理解】如图①,在△ABC中,∠A=36°,∠C=72°,请你在这个三角形中画出它的“好线”,并标出等腰三角形顶角的度数.
如图②,已知△ABC是一个顶角为45°的等腰三角形,请你在这个三角形中画出它的“好好线”,并标出所分得的等腰三角形底角的度数.
【应用】
(1)在△ABC中,已知一个内角为42°,若它只有“好线”,请你写出这个三角形最大内角的所有可能值 ;
(2)在△ABC中,∠C=27°,AD和DE分别是△ABC的“好好线”,点D在BC边上,点E在AB边上,且AD=DC,BE=DE,请你根据题意画出示意图,并求∠B的度数.
教师样卷
一.选择题(每小题3分 共30分)
1.第24届冬季奥林匹克运动会于2022年02月04日~2022年02月20日在中华人民共和国北京市和张家口市联合举行.在会徽的图案设计中,设计者常常利用对称性进行设计,下列四个图案是历届会徽图案上的一部份图形,其中不是轴对称图形的是( )
A.B. C.D.
第1题图 第3题图
【答案】D 解:A、是轴对称图形,故此选项错误;B、是轴对称图形,故此选项错误;C、是轴对称图形,故此选项错误;D、不是轴对称图形,故此选项正确;故选:D.
2.在下列各组条件中,不能说明△ABC≌△DEF的是( )
A.AB=DE,∠B=∠E,∠C=∠F B.AC=DF,BC=EF,∠A=∠D
C.AB=DE,∠A=∠D,∠B=∠E D.AB=DE,BC=EF,AC=DF
【答案】B 解:A、AB=DE,∠B=∠E,∠C=∠F,可以利用AAS定理证明△ABC≌△DEF,故此选项不合题意;B、AC=DF,BC=EF,∠A=∠D不能证明△ABC≌△DEF,故此选项符合题意;C、AB=DE,∠A=∠D,∠B=∠E,可以利用ASA定理证明△ABC≌△DEF,故此选项不合题意;D、AB=DE,BC=EF,AC=DF可以利用SSS定理证明△ABC≌△DEF,故此选项不合题意;故选:B.
3.如图,在△ABC中,AB=AC,D、E两点分别在AC、BC上,BD是∠ABC的平分线,DE∥AB,若BE=5cm,CE=3cm,则△CDE的周长是( )
A.15cm B.13cm C.11cm D.9cm
【答案】B解:∵AB=AC,∴∠ABC=∠C.∵DE∥AB,∴∠DEC=∠ABC=∠C,∠ABD=∠BDE,
∴DE=DC,∵BD是∠ABC的平分线,∴∠ABD=∠DBE.∴∠DBE=∠BDE,∴BE=DE=DC=5cm,
∴△CDE的周长为DE+DC+EC=5+5+3=13(cm),故选:B.
4.下列各式从左到右的变形属于因式分解的是 ( )
A.a(x+y) =ax+ay B.10x2-5x=5x(2x-1)
C.x2-4x+4=x(x-4+) D.x2-16+3x=(x-4)(x+4)+3x
【答案】B
5.下列运算中,计算结果正确的是( ).
A. B. C. D.
【答案】D
6.如图,根据图形的面积,可以验证一个乘法公式,这个公式是( )A. B. C. D.
【答案】D
7.以下图形中对称轴的数量小于3的是( )
A. B. C. D.
第7题图 第8题图
【答案】D解:A、有4条对称轴;B、有6条对称轴;C、有4条对称轴;D、有2条对称轴.故选:D.
8.如图,∠C=∠D=90°,AC=AD,那么△ABC与△ABD全等的理由是( )
A.HL B.SAS C.ASA D.AAS
【答案】A解:在Rt△ABC与Rt△ABD中,∴Rt△ABC≌Rt△ABD(HL)故选:A.
9.如图,在△ABC中,AC的垂直平分线分别交AB、AC于点D、E,EC=5,△ABC的周长为26,则△BDC的周长为( )
A.14 B.16 C.18 D.19
第9题图 第10题图 第11题图 第12题图
【答案】B 解:∵DE是AC的垂直平分线,∴DA=DC,AC=2EC=10,∵△ABC的周长为26,∴AB+AC+BC=26,∴AB+BC=16,∴△BDC的周长=BD+CD+BC=BD+AD+BC=AB+BC=16,故选:B.
10.如图,在2×3的正方形网络中,有一个以格点为顶点的三角形,此网格中所有与该三角形成轴对称且以格点为顶点的三角形共有( )
A.1个 B.2个 C.3个 D.4个
【答案】C 解:如图,与△ABE成轴对称的格点三角形有△ABF、△AEF、△EBC共3个,
故选:C.
二.题空题(每小题3分 共30分)
11.如图,在Rt△ABC 中,∠C=90°,沿过点A的一条直线AE折叠Rt△ABC,使点C恰好落在AB边的中点D处,则∠B的度数是_______
【答案】30°解:由折叠,可知:∠CAE=∠DAE,∠ADE=∠C=90°,∴ED⊥AB.
∵点D为线段AB的中点,ED⊥AB,∴AE=BE,∴∠B=∠DAE.又∵∠CAE+∠DAE+∠B+∠C=180°,∴3∠B=9°,∴∠B=30°.
12.如图,已知AB=2,BF=8,BC=AE=6,CE=CF=7,则△CDF与四边形ABDE的面积比值是_______
【答案】1:1 解:由题意得AC=CB+BA=8,∴AC=BF,在△AEC和△BCF中,
∴△AEC≌△BCF(SSS),∴S△AEC=S△BCF,故可得S△CDF+S△CDB=SABDE+S△CDB S四边形ABDE=S△CDF,∴四边形ABDE与△CDF面积的比值是1:1.
13.分解因式:= .
【答案】
14.若,,则 = .
【答案】 3
15.若等腰三角形的两边的边长分别为10cm和5cm,则第三边的长是 cm.
【答案】10 解:若10cm为腰长,则第三边的长是10cm;若5cm为腰长,∵5+5=10,
∴不能组成三角形,舍去;综上:若等腰三角形的两边的边长分别为10cm和5cm,则第三边的长是10cm.故答案为:10.
16.如图,AB=AC,点D,E分别在AB,AC上,CD,BE交于点F,只添加一个条件使△ABE≌△ACD,添加的条件是: .
【答案】∠B=∠C 解:∠B=∠C,理由是:∵在△ABE和△ACD中∴△ABE≌△ACD(ASA),故答案为:∠B=∠C.
第16题图 第17题图 第18题图 第19题图 第20题图
17.如图,在△ABC中,AB=AC.以点C为圆心,以CB长为半径作圆弧,交AC的延长线于点D,连结BD.若∠A=32°,则∠CDB的大小为 度.
【答案】37 解:∵AB=AC,∠A=32°,∴∠ABC=∠ACB=74°,又∵BC=DC,∴∠CDB=∠CBD=∠ACB=37°.故答案为:37.
18.如图,在△ABC中,∠ACB=90°,D是AB边的中点若AB=18,则CD的长为 .
【答案】9 解:∠ACB=90°,D是AB边的中点,∴CD=AB=9,故答案为:9.
19.把一个长方形纸片按如图所示折叠,若量得∠AOD′=36°,则∠D′OE的度数为 .
【答案】72°解:∵四边形ODCE折叠后形成四边形OD′C′E,∴∠D′OE=∠DOE,
∴∠AOD′+2∠D′OE=180°,∵∠AOD′=36°,∴∠D′OE=72°.故答案为:72°.
20.如图,在△ABC中,∠ACB=90°,∠A=30°,AB=5,点P是AC上的动点,连接BP,以BP为边作等边△BPQ,连接CQ,则点P在运动过程中,线段CQ长度的最小值是 .
【答案】 解:如图,取AB的中点E,连接CE,PE.∵∠ACB=90°,∠A=30°,∴∠CBE=60°,∵BE=AE,∴CE=BE=AE,∴△BCE是等边三角形,∴BC=BE,∵∠PBQ=∠CBE=60°,∴∠QBC=∠PBE,∵QB=PB,CB=EB,∴△QBC≌△PBE(SAS),∴QC=PE,∴当EP⊥AC时,QC的值最小,在Rt△AEP中,∵AE=,∠A=30°,∴PE=AE=,∴CQ的最小值为.
三.解答题(60分)
21.(12分)计算:
(1); (2) ;
(3); (4).
【答案】(1)解:原式
(2) 解:原式
(3)解:原式
(4)解:原式
22.(6分)先化简,再求值:,其中a=2,b=1.
解:原式
当时原式= =12
23.(6分)如图,点E在线段AC上,BC∥DE,AC=DE,CB=CE,求证:∠A=∠D.
【解答】证明:∵BC∥DE,∴∠BCA=∠CED,在△ABC和△DCE中,
,∴△ABC≌△DCE(SAS),∴∠A=∠D.
24.(8分)在等腰△ABC中,已知AB=AC,BD⊥AC于D.
(1)若∠A=48°,求∠CBD的度数; (2)若BC=15,BD=12,求AB的长.
【解答】解:(1)∵在等腰△ABC中,AB=AC,BD⊥AC,∴∠ABC=∠C,∠ADB=90°,
∵∠A=48°,∴∠ABC=∠C=66°,∠ABD=42°,∴∠CBD=24°;
(2)∵BD⊥AC,∴∠BDC=90°,∵BC=15,BD=12,∴CD=9,设AB=x,则AD=x﹣9,∵∠ADB=90°,BD=12,∴122+(x﹣9)2=x2,解得,x=,即AB=.
25.(8分)已知两个等腰直角△ABC和△CDE,它们的两个直角顶点B、D在直线MN上,过点A、E分别作AG⊥MN,EF⊥MN,垂足分别为G、F.
(1)如图1,当△ABC和△CDE在△BCD的外部时,请你探索线段EF、DB、AG之间的数量关系,其数量关系为 BD=EF+AG. .
(2)如图2,将图1中的△ABC沿BC翻折,其他条件不变,那么(1)中的结论是否仍然成立?若成立,请你给出证明,若不成立,请探索它们的数量关系,并说明理由.
【解答】解:(1)结论:BD=EF+AG.理由:如图1中,作CH⊥MN于H.∵EF⊥MN,AG⊥MN,∴∠EFD=∠EDC=∠CHD=90°,∴∠EDF+∠CDH=90°,∠CDH+∠DCH=90°,∴∠EDF=∠DCH,∵DE=DC,∴△FDE≌△HCD(AAS),∴EF=DH,
同理可证:△BHC≌△AGB,∴AG=BH,∴BD=EF+AG.故答案为BD=EF+AG.
(2)结论不变.理由:如图2中,作CH⊥MN于H.∵EF⊥MN,AG⊥MN,∴∠EFD=∠EDC=∠CHD=90°,∴∠EDF+∠CDH=90°,∠CDH+∠DCH=90°,∴∠EDF=∠DCH,∵DE=DC,∴△FDE≌△HCD(AAS),∴EF=DH,同理可证:△BHC≌△AGB,∴AG=BH,∴BD=EF+AG.故答案为BD=EF+AG.
26.(10分)画图计算:
(1)已知△ABC,请用尺规在图1中△ABC内确定一个点P,使得点P到AB和BC的距离相等,且满足P到点B和点C的距离相等(不写作法,保留作图痕迹).
(2)如图2,如果点P是(1)中求作的点,点E、F分别在边AB、BC上,且PE=PF.
①若∠ABC=60°,求∠EPF的度数;
②若BE=2,BF=8,EP=5,求BP的长.
(3)如图3,如果点P是△ABC内一点,且点P到点B的距离是7,若∠ABC=45°,请分别在AB、BC上求作两个点M、N,使得△PMN的周长最小(不写作法,保留作图痕迹),则△PMN的最小值为 7
【解答】解:(1)如图,点P即为所求;
(2)①连接BP,作PM⊥AB于M,PN⊥BC于N.∵BP平分∠ABC,PM⊥AB,PN⊥BC,
∴PM=PN,∵PE=PF,∠PME=∠PNF=90°,∴Rt△PME≌Rt△PNF(HL),∴∠EPM=∠FPN,∴∠EPF=∠MPN,∵∠MPN=360°﹣90°﹣90°﹣60°=120°,∴∠EPF=120°.
②∵PB=PB,PM=PN,∠PMB=∠PFB=90°∴Rt△PMB≌Rt△PNB(HL),∴BM=BN,
∵Rt△PME≌Rt△PNF(HL),∴EM=FN,∴BE+BF=BM﹣EM+BN+NF=2BN=10,
∴BN=NM=5,∵BE=2,PE=5,∴EM=3,PM==4,∴BP==.
(3)分别作点P关于边AB、BC的对称点E、F,连接EF,分别与边AB、BC交于点M、N,连接PM、PN.则线段EF的长度即为△PMN的周长的最小值.∵点E与点P关于AB对称,点F与点P关于BC对称,∴∠EBA=∠PBA,∠FBC=∠PBC,BE=BF=BP=7.
∴EF=BE=7∴△PMN周长的最小值为7.故答案为7.
27.(10分)【定义】数学课上,陈老师对我们说,如果1条线段将一个三角形分成2个等腰三角形,那么这1条线段就称为这个三角形的“好线”,如果2条线段将一个三角形分成3个等腰三角形,那么这2条线段就称为这个三角形的“好好线”.【理解】如图①,在△ABC中,∠A=36°,∠C=72°,请你在这个三角形中画出它的“好线”,并标出等腰三角形顶角的度数.
如图②,已知△ABC是一个顶角为45°的等腰三角形,请你在这个三角形中画出它的“好好线”,并标出所分得的等腰三角形底角的度数.
【应用】
(1)在△ABC中,已知一个内角为42°,若它只有“好线”,请你写出这个三角形最大内角的所有可能值 84°或103.5°或124°或117°或126° ;
(2)在△ABC中,∠C=27°,AD和DE分别是△ABC的“好好线”,点D在BC边上,点E在AB边上,且AD=DC,BE=DE,请你根据题意画出示意图,并求∠B的度数.
【解答】解:【定义】如图①,如图②所示,
【应用】(1)①如图③当∠B=42°,AD为“好线”,则AD=AD=BD,故这个三角形最大内角是∠C=84°;②如图④当∠B=42°,AD为“好线”,
则AB=AD,AD=CD,这个三角形最大内角是∠BAC=103.5°;
③如图⑤当∠ABC=42°时,BD为“好线”,则AD=BD,CD=BC,故这个三角形最大内角是∠C=124°,④如图⑥,当∠B=42°时,CD为“好线”,
则AD=CD=BC,故这个三角形最大内角是∠ACB=117°,
⑤如图⑦,当∠B=42°时,CD为“好线”,则AD=AC,CD=BD,故这个三角形最大内角是∠ACB=126°,综上所述,这个三角形最大内角的所有可能值是84°或103.5°或124°或117°或126°,故答案为:84°或103.5°或124°或117°或126°;
(2)设∠B=x°,①当AD=DE时,如图1(a),∵AD=CD,∴∠C=∠CAD=27°,
∵DE=EB,∴∠B=∠EDB=x°∴∠AED=∠DAE=2x°,∴27×2+2x+x=180,∴x=42,
∴∠B=42°;
②当AD=AE时,如图1(b),∵AD=CD,∴∠C=∠CAD=27°,∵DE=EB,∴∠B=∠EDB=x°∴∠AED=∠ADE=2x°,∴2x+x=27+27,∴x=18,∴∠B=18°.
③当EA=DE时,∵90﹣x+27+27+x=180,∴x不存在,应舍去.综合上述:满足条件的x=42°或18°.
(时间:90分钟 满分:120分)
一.选择题(每小题3分 共30分)
1.第24届冬季奥林匹克运动会于2022年02月04日~2022年02月20日在中华人民共和国北京市和张家口市联合举行.在会徽的图案设计中,设计者常常利用对称性进行设计,下列四个图案是历届会徽图案上的一部份图形,其中不是轴对称图形的是( )
A.B. C.D.
第1题图 第3题图
2.在下列各组条件中,不能说明△ABC≌△DEF的是( )
A.AB=DE,∠B=∠E,∠C=∠F B.AC=DF,BC=EF,∠A=∠D
C.AB=DE,∠A=∠D,∠B=∠E D.AB=DE,BC=EF,AC=DF
3.如图,在△ABC中,AB=AC,D、E两点分别在AC、BC上,BD是∠ABC的平分线,DE∥AB,若BE=5cm,CE=3cm,则△CDE的周长是( )
A.15cm B.13cm C.11cm D.9cm
4.下列各式从左到右的变形属于因式分解的是 ( )
A.a(x+y) =ax+ay B.10x2-5x=5x(2x-1)
C.x2-4x+4=x(x-4+) D.x2-16+3x=(x-4)(x+4)+3x
5.下列运算中,计算结果正确的是( ).
A. B. C. D.
6.如图,根据图形的面积,可以验证一个乘法公式,这个公式是( )A. B. C. D.
7.以下图形中对称轴的数量小于3的是( )
A. B. C. D.
第7题图 第8题图
8.如图,∠C=∠D=90°,AC=AD,那么△ABC与△ABD全等的理由是( )
A.HL B.SAS C.ASA D.AAS
9.如图,在△ABC中,AC的垂直平分线分别交AB、AC于点D、E,EC=5,△ABC的周长为26,则△BDC的周长为( )
A.14 B.16 C.18 D.19
第9题图 第10题图 第11题图 第12题图
10.如图,在2×3的正方形网络中,有一个以格点为顶点的三角形,此网格中所有与该三角形成轴对称且以格点为顶点的三角形共有( )
A.1个 B.2个 C.3个 D.4个
二.题空题(每小题3分 共30分)
11.如图,在Rt△ABC 中,∠C=90°,沿过点A的一条直线AE折叠Rt△ABC,使点C恰好落在AB边的中点D处,则∠B的度数是_______
12.如图,已知AB=2,BF=8,BC=AE=6,CE=CF=7,则△CDF与四边形ABDE的面积比值是_______
13.分解因式:= .
14.若,,则 = .
15.若等腰三角形的两边的边长分别为10cm和5cm,则第三边的长是 cm.
16.如图,AB=AC,点D,E分别在AB,AC上,CD,BE交于点F,只添加一个条件使△ABE≌△ACD,添加的条件是: .
第16题图 第17题图 第18题图 第19题图 第20题图
17.如图,在△ABC中,AB=AC.以点C为圆心,以CB长为半径作圆弧,交AC的延长线于点D,连结BD.若∠A=32°,则∠CDB的大小为 度.
18.如图,在△ABC中,∠ACB=90°,D是AB边的中点若AB=18,则CD的长为 .
19.把一个长方形纸片按如图所示折叠,若量得∠AOD′=36°,则∠D′OE的度数为 .
20.如图,在△ABC中,∠ACB=90°,∠A=30°,AB=5,点P是AC上的动点,连接BP,以BP为边作等边△BPQ,连接CQ,则点P在运动过程中,线段CQ长度的最小值是 .
三.解答题(60分)
21.(12分)计算:
(1); (2) ;
(3); (4).
22.(6分)先化简,再求值:,其中a=2,b=1.
23.(6分)如图,点E在线段AC上,BC∥DE,AC=DE,CB=CE,求证:∠A=∠D.
24.(8分)在等腰△ABC中,已知AB=AC,BD⊥AC于D.
(1)若∠A=48°,求∠CBD的度数;
(2)若BC=15,BD=12,求AB的长.
25.(8分)已知两个等腰直角△ABC和△CDE,它们的两个直角顶点B、D在直线MN上,过点A、E分别作AG⊥MN,EF⊥MN,垂足分别为G、F.
(1)如图1,当△ABC和△CDE在△BCD的外部时,请你探索线段EF、DB、AG之间的数量关系,其数量关系为 .
(2)如图2,将图1中的△ABC沿BC翻折,其他条件不变,那么(1)中的结论是否仍然成立?若成立,请你给出证明,若不成立,请探索它们的数量关系,并说明理由.
26.(10分)画图计算:
(1)已知△ABC,请用尺规在图1中△ABC内确定一个点P,使得点P到AB和BC的距离相等,且满足P到点B和点C的距离相等(不写作法,保留作图痕迹).
(2)如图2,如果点P是(1)中求作的点,点E、F分别在边AB、BC上,且PE=PF.
①若∠ABC=60°,求∠EPF的度数;
②若BE=2,BF=8,EP=5,求BP的长.
如图3,如果点P是△ABC内一点,且点P到点B的距离是7,若∠ABC=45°,请分别在AB、BC上求作两个点M、N,使得△PMN的周长最小(不写作法,保留作图痕迹),则△PMN的最小值为
(10分)【定义】数学课上,陈老师对我们说,如果1条线段将一个三角形分成2个等腰三角形,那么这1条线段就称为这个三角形的“好线”,如果2条线段将一个三角形分成3个等腰三角形,那么这2条线段就称为这个三角形的“好好线”.
【理解】如图①,在△ABC中,∠A=36°,∠C=72°,请你在这个三角形中画出它的“好线”,并标出等腰三角形顶角的度数.
如图②,已知△ABC是一个顶角为45°的等腰三角形,请你在这个三角形中画出它的“好好线”,并标出所分得的等腰三角形底角的度数.
【应用】
(1)在△ABC中,已知一个内角为42°,若它只有“好线”,请你写出这个三角形最大内角的所有可能值 ;
(2)在△ABC中,∠C=27°,AD和DE分别是△ABC的“好好线”,点D在BC边上,点E在AB边上,且AD=DC,BE=DE,请你根据题意画出示意图,并求∠B的度数.
教师样卷
一.选择题(每小题3分 共30分)
1.第24届冬季奥林匹克运动会于2022年02月04日~2022年02月20日在中华人民共和国北京市和张家口市联合举行.在会徽的图案设计中,设计者常常利用对称性进行设计,下列四个图案是历届会徽图案上的一部份图形,其中不是轴对称图形的是( )
A.B. C.D.
第1题图 第3题图
【答案】D 解:A、是轴对称图形,故此选项错误;B、是轴对称图形,故此选项错误;C、是轴对称图形,故此选项错误;D、不是轴对称图形,故此选项正确;故选:D.
2.在下列各组条件中,不能说明△ABC≌△DEF的是( )
A.AB=DE,∠B=∠E,∠C=∠F B.AC=DF,BC=EF,∠A=∠D
C.AB=DE,∠A=∠D,∠B=∠E D.AB=DE,BC=EF,AC=DF
【答案】B 解:A、AB=DE,∠B=∠E,∠C=∠F,可以利用AAS定理证明△ABC≌△DEF,故此选项不合题意;B、AC=DF,BC=EF,∠A=∠D不能证明△ABC≌△DEF,故此选项符合题意;C、AB=DE,∠A=∠D,∠B=∠E,可以利用ASA定理证明△ABC≌△DEF,故此选项不合题意;D、AB=DE,BC=EF,AC=DF可以利用SSS定理证明△ABC≌△DEF,故此选项不合题意;故选:B.
3.如图,在△ABC中,AB=AC,D、E两点分别在AC、BC上,BD是∠ABC的平分线,DE∥AB,若BE=5cm,CE=3cm,则△CDE的周长是( )
A.15cm B.13cm C.11cm D.9cm
【答案】B解:∵AB=AC,∴∠ABC=∠C.∵DE∥AB,∴∠DEC=∠ABC=∠C,∠ABD=∠BDE,
∴DE=DC,∵BD是∠ABC的平分线,∴∠ABD=∠DBE.∴∠DBE=∠BDE,∴BE=DE=DC=5cm,
∴△CDE的周长为DE+DC+EC=5+5+3=13(cm),故选:B.
4.下列各式从左到右的变形属于因式分解的是 ( )
A.a(x+y) =ax+ay B.10x2-5x=5x(2x-1)
C.x2-4x+4=x(x-4+) D.x2-16+3x=(x-4)(x+4)+3x
【答案】B
5.下列运算中,计算结果正确的是( ).
A. B. C. D.
【答案】D
6.如图,根据图形的面积,可以验证一个乘法公式,这个公式是( )A. B. C. D.
【答案】D
7.以下图形中对称轴的数量小于3的是( )
A. B. C. D.
第7题图 第8题图
【答案】D解:A、有4条对称轴;B、有6条对称轴;C、有4条对称轴;D、有2条对称轴.故选:D.
8.如图,∠C=∠D=90°,AC=AD,那么△ABC与△ABD全等的理由是( )
A.HL B.SAS C.ASA D.AAS
【答案】A解:在Rt△ABC与Rt△ABD中,∴Rt△ABC≌Rt△ABD(HL)故选:A.
9.如图,在△ABC中,AC的垂直平分线分别交AB、AC于点D、E,EC=5,△ABC的周长为26,则△BDC的周长为( )
A.14 B.16 C.18 D.19
第9题图 第10题图 第11题图 第12题图
【答案】B 解:∵DE是AC的垂直平分线,∴DA=DC,AC=2EC=10,∵△ABC的周长为26,∴AB+AC+BC=26,∴AB+BC=16,∴△BDC的周长=BD+CD+BC=BD+AD+BC=AB+BC=16,故选:B.
10.如图,在2×3的正方形网络中,有一个以格点为顶点的三角形,此网格中所有与该三角形成轴对称且以格点为顶点的三角形共有( )
A.1个 B.2个 C.3个 D.4个
【答案】C 解:如图,与△ABE成轴对称的格点三角形有△ABF、△AEF、△EBC共3个,
故选:C.
二.题空题(每小题3分 共30分)
11.如图,在Rt△ABC 中,∠C=90°,沿过点A的一条直线AE折叠Rt△ABC,使点C恰好落在AB边的中点D处,则∠B的度数是_______
【答案】30°解:由折叠,可知:∠CAE=∠DAE,∠ADE=∠C=90°,∴ED⊥AB.
∵点D为线段AB的中点,ED⊥AB,∴AE=BE,∴∠B=∠DAE.又∵∠CAE+∠DAE+∠B+∠C=180°,∴3∠B=9°,∴∠B=30°.
12.如图,已知AB=2,BF=8,BC=AE=6,CE=CF=7,则△CDF与四边形ABDE的面积比值是_______
【答案】1:1 解:由题意得AC=CB+BA=8,∴AC=BF,在△AEC和△BCF中,
∴△AEC≌△BCF(SSS),∴S△AEC=S△BCF,故可得S△CDF+S△CDB=SABDE+S△CDB S四边形ABDE=S△CDF,∴四边形ABDE与△CDF面积的比值是1:1.
13.分解因式:= .
【答案】
14.若,,则 = .
【答案】 3
15.若等腰三角形的两边的边长分别为10cm和5cm,则第三边的长是 cm.
【答案】10 解:若10cm为腰长,则第三边的长是10cm;若5cm为腰长,∵5+5=10,
∴不能组成三角形,舍去;综上:若等腰三角形的两边的边长分别为10cm和5cm,则第三边的长是10cm.故答案为:10.
16.如图,AB=AC,点D,E分别在AB,AC上,CD,BE交于点F,只添加一个条件使△ABE≌△ACD,添加的条件是: .
【答案】∠B=∠C 解:∠B=∠C,理由是:∵在△ABE和△ACD中∴△ABE≌△ACD(ASA),故答案为:∠B=∠C.
第16题图 第17题图 第18题图 第19题图 第20题图
17.如图,在△ABC中,AB=AC.以点C为圆心,以CB长为半径作圆弧,交AC的延长线于点D,连结BD.若∠A=32°,则∠CDB的大小为 度.
【答案】37 解:∵AB=AC,∠A=32°,∴∠ABC=∠ACB=74°,又∵BC=DC,∴∠CDB=∠CBD=∠ACB=37°.故答案为:37.
18.如图,在△ABC中,∠ACB=90°,D是AB边的中点若AB=18,则CD的长为 .
【答案】9 解:∠ACB=90°,D是AB边的中点,∴CD=AB=9,故答案为:9.
19.把一个长方形纸片按如图所示折叠,若量得∠AOD′=36°,则∠D′OE的度数为 .
【答案】72°解:∵四边形ODCE折叠后形成四边形OD′C′E,∴∠D′OE=∠DOE,
∴∠AOD′+2∠D′OE=180°,∵∠AOD′=36°,∴∠D′OE=72°.故答案为:72°.
20.如图,在△ABC中,∠ACB=90°,∠A=30°,AB=5,点P是AC上的动点,连接BP,以BP为边作等边△BPQ,连接CQ,则点P在运动过程中,线段CQ长度的最小值是 .
【答案】 解:如图,取AB的中点E,连接CE,PE.∵∠ACB=90°,∠A=30°,∴∠CBE=60°,∵BE=AE,∴CE=BE=AE,∴△BCE是等边三角形,∴BC=BE,∵∠PBQ=∠CBE=60°,∴∠QBC=∠PBE,∵QB=PB,CB=EB,∴△QBC≌△PBE(SAS),∴QC=PE,∴当EP⊥AC时,QC的值最小,在Rt△AEP中,∵AE=,∠A=30°,∴PE=AE=,∴CQ的最小值为.
三.解答题(60分)
21.(12分)计算:
(1); (2) ;
(3); (4).
【答案】(1)解:原式
(2) 解:原式
(3)解:原式
(4)解:原式
22.(6分)先化简,再求值:,其中a=2,b=1.
解:原式
当时原式= =12
23.(6分)如图,点E在线段AC上,BC∥DE,AC=DE,CB=CE,求证:∠A=∠D.
【解答】证明:∵BC∥DE,∴∠BCA=∠CED,在△ABC和△DCE中,
,∴△ABC≌△DCE(SAS),∴∠A=∠D.
24.(8分)在等腰△ABC中,已知AB=AC,BD⊥AC于D.
(1)若∠A=48°,求∠CBD的度数; (2)若BC=15,BD=12,求AB的长.
【解答】解:(1)∵在等腰△ABC中,AB=AC,BD⊥AC,∴∠ABC=∠C,∠ADB=90°,
∵∠A=48°,∴∠ABC=∠C=66°,∠ABD=42°,∴∠CBD=24°;
(2)∵BD⊥AC,∴∠BDC=90°,∵BC=15,BD=12,∴CD=9,设AB=x,则AD=x﹣9,∵∠ADB=90°,BD=12,∴122+(x﹣9)2=x2,解得,x=,即AB=.
25.(8分)已知两个等腰直角△ABC和△CDE,它们的两个直角顶点B、D在直线MN上,过点A、E分别作AG⊥MN,EF⊥MN,垂足分别为G、F.
(1)如图1,当△ABC和△CDE在△BCD的外部时,请你探索线段EF、DB、AG之间的数量关系,其数量关系为 BD=EF+AG. .
(2)如图2,将图1中的△ABC沿BC翻折,其他条件不变,那么(1)中的结论是否仍然成立?若成立,请你给出证明,若不成立,请探索它们的数量关系,并说明理由.
【解答】解:(1)结论:BD=EF+AG.理由:如图1中,作CH⊥MN于H.∵EF⊥MN,AG⊥MN,∴∠EFD=∠EDC=∠CHD=90°,∴∠EDF+∠CDH=90°,∠CDH+∠DCH=90°,∴∠EDF=∠DCH,∵DE=DC,∴△FDE≌△HCD(AAS),∴EF=DH,
同理可证:△BHC≌△AGB,∴AG=BH,∴BD=EF+AG.故答案为BD=EF+AG.
(2)结论不变.理由:如图2中,作CH⊥MN于H.∵EF⊥MN,AG⊥MN,∴∠EFD=∠EDC=∠CHD=90°,∴∠EDF+∠CDH=90°,∠CDH+∠DCH=90°,∴∠EDF=∠DCH,∵DE=DC,∴△FDE≌△HCD(AAS),∴EF=DH,同理可证:△BHC≌△AGB,∴AG=BH,∴BD=EF+AG.故答案为BD=EF+AG.
26.(10分)画图计算:
(1)已知△ABC,请用尺规在图1中△ABC内确定一个点P,使得点P到AB和BC的距离相等,且满足P到点B和点C的距离相等(不写作法,保留作图痕迹).
(2)如图2,如果点P是(1)中求作的点,点E、F分别在边AB、BC上,且PE=PF.
①若∠ABC=60°,求∠EPF的度数;
②若BE=2,BF=8,EP=5,求BP的长.
(3)如图3,如果点P是△ABC内一点,且点P到点B的距离是7,若∠ABC=45°,请分别在AB、BC上求作两个点M、N,使得△PMN的周长最小(不写作法,保留作图痕迹),则△PMN的最小值为 7
【解答】解:(1)如图,点P即为所求;
(2)①连接BP,作PM⊥AB于M,PN⊥BC于N.∵BP平分∠ABC,PM⊥AB,PN⊥BC,
∴PM=PN,∵PE=PF,∠PME=∠PNF=90°,∴Rt△PME≌Rt△PNF(HL),∴∠EPM=∠FPN,∴∠EPF=∠MPN,∵∠MPN=360°﹣90°﹣90°﹣60°=120°,∴∠EPF=120°.
②∵PB=PB,PM=PN,∠PMB=∠PFB=90°∴Rt△PMB≌Rt△PNB(HL),∴BM=BN,
∵Rt△PME≌Rt△PNF(HL),∴EM=FN,∴BE+BF=BM﹣EM+BN+NF=2BN=10,
∴BN=NM=5,∵BE=2,PE=5,∴EM=3,PM==4,∴BP==.
(3)分别作点P关于边AB、BC的对称点E、F,连接EF,分别与边AB、BC交于点M、N,连接PM、PN.则线段EF的长度即为△PMN的周长的最小值.∵点E与点P关于AB对称,点F与点P关于BC对称,∴∠EBA=∠PBA,∠FBC=∠PBC,BE=BF=BP=7.
∴EF=BE=7∴△PMN周长的最小值为7.故答案为7.
27.(10分)【定义】数学课上,陈老师对我们说,如果1条线段将一个三角形分成2个等腰三角形,那么这1条线段就称为这个三角形的“好线”,如果2条线段将一个三角形分成3个等腰三角形,那么这2条线段就称为这个三角形的“好好线”.【理解】如图①,在△ABC中,∠A=36°,∠C=72°,请你在这个三角形中画出它的“好线”,并标出等腰三角形顶角的度数.
如图②,已知△ABC是一个顶角为45°的等腰三角形,请你在这个三角形中画出它的“好好线”,并标出所分得的等腰三角形底角的度数.
【应用】
(1)在△ABC中,已知一个内角为42°,若它只有“好线”,请你写出这个三角形最大内角的所有可能值 84°或103.5°或124°或117°或126° ;
(2)在△ABC中,∠C=27°,AD和DE分别是△ABC的“好好线”,点D在BC边上,点E在AB边上,且AD=DC,BE=DE,请你根据题意画出示意图,并求∠B的度数.
【解答】解:【定义】如图①,如图②所示,
【应用】(1)①如图③当∠B=42°,AD为“好线”,则AD=AD=BD,故这个三角形最大内角是∠C=84°;②如图④当∠B=42°,AD为“好线”,
则AB=AD,AD=CD,这个三角形最大内角是∠BAC=103.5°;
③如图⑤当∠ABC=42°时,BD为“好线”,则AD=BD,CD=BC,故这个三角形最大内角是∠C=124°,④如图⑥,当∠B=42°时,CD为“好线”,
则AD=CD=BC,故这个三角形最大内角是∠ACB=117°,
⑤如图⑦,当∠B=42°时,CD为“好线”,则AD=AC,CD=BD,故这个三角形最大内角是∠ACB=126°,综上所述,这个三角形最大内角的所有可能值是84°或103.5°或124°或117°或126°,故答案为:84°或103.5°或124°或117°或126°;
(2)设∠B=x°,①当AD=DE时,如图1(a),∵AD=CD,∴∠C=∠CAD=27°,
∵DE=EB,∴∠B=∠EDB=x°∴∠AED=∠DAE=2x°,∴27×2+2x+x=180,∴x=42,
∴∠B=42°;
②当AD=AE时,如图1(b),∵AD=CD,∴∠C=∠CAD=27°,∵DE=EB,∴∠B=∠EDB=x°∴∠AED=∠ADE=2x°,∴2x+x=27+27,∴x=18,∴∠B=18°.
③当EA=DE时,∵90﹣x+27+27+x=180,∴x不存在,应舍去.综合上述:满足条件的x=42°或18°.
同课章节目录
