2022-2023学年人教版八年级数学上册 13.3等腰三角形 同步练习题 (word版 含解析)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册 13.3等腰三角形 同步练习题 (word版 含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 131.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-24 14:43:26 | ||
图片预览



文档简介
2022-2023学年人教版八年级数学上册《13.3等腰三角形》同步练习题(附答案)
一.选择题
1.如图,在△ABC中,AB=AC=2,∠B=60°,AD平分∠BAC,则AD等于( )
A.1 B. C. D.1.5
2.如图,在钝角三角形ABC中,∠ABC为钝角,以点B为圆心,AB长为半径画弧;再以点C为圆心,AC长为半径画弧;两弧交于点D,连接AD,CB的延长线交AD于点E.下列结论错误的是( )
A.CE垂直平分AD B.CE平分∠ACD
C.△ABD是等腰三角形 D.△ACD是等边三角形
3.如图,把一张长方形纸片沿对角线折叠,若△EDF是等腰三角形,则∠BDC=( )
A.45° B.60° C.67.5° D.75°
4.如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=8,则线段MN的长为( )
A.6 B.7 C.8 D.9
5.如图,等边△ABC的边长为2,AD是BC边上的高,则高AD的长为( )
A.1 B. C. D.2
6.一个等腰三角形的两边长分别是2、4,那么它的周长是( )
A.10 B.8 C.10或8 D.不能确定
7.已知等腰三角形的周长是20,其中一边长为6,则其它两边的长度分别是( )
A.6和8 B.7和7 C.6和8或7和7 D.3和11
8.如图,在△ABC中,点D在BC边上,BD=AD=AC,E为CD的中点,若∠CAE=16°,则∠B的大小为( )
A.32° B.36° C.37° D.74°
9.如图,△ABC中,AB=AC,∠B=30°,点D是AC的中点,过点D作DE⊥AC交BC于点E,连接EA.则∠BAE的度数为( )
A.30° B.80° C.90° D.110°
10.如图,在△ABC中,AB=AC,AD、CE分别是△ABC的中线和角平分线.若∠CAD=20°,则∠ACE的度数是( )
A.20° B.35° C.40° D.70°
11.等腰三角形周长为18,其中一边长为4,则其它两边长分别为( )
A.4,10 B.7,7 C.4,10或7,7 D.无法确定
12.等腰三角形的顶角比每个底角大30°,则这个等腰三角形的顶角是( )
A.40° B.50° C.80° D.85°
二.填空题
13.已知等腰△ABC中,AB=AC,∠B=50°,则∠A= 度.
14.如图,在△ABC中,∠ABC的平分线与∠ACB的平分线交于点D,过点D作BC的平行线交AB于点E,交AC于点F,已知∠BED+∠CFD=240°,则∠BDC= .
15.在△ABC中,∠C=90°,AC=8cm,BC=6cm.动点P从点C开始按C→A→B→C的路径绕△ABC的边运动一周,速度为每秒2cm,运动的时间为t秒.则△BCP为等腰三角形时t的值是 .
16.如图,△ABC中,D是BC上一点,AC=AD=BD,若∠DAC=84°,则∠B= 度.
三.解答题
17.已知△ABC,AB=AC,D为BC上一点,E为AC上一点,AD=AE.
(1)如果∠BAD=10°,∠DAE=30°,那么∠EDC= °.
(2)如果∠ABC=60°,∠ADE=70°,那么∠BAD= °,∠CDE= °.
(3)设∠BAD=α,∠CDE=β猜想α,β之间的关系式,并说明理由.
18.数学课上,张老师举了下面的例题:
例1:等腰△ABC中,∠A=100°,求∠B的度数(答案:40°)
例2:等腰△ABC中,∠A=50°,求∠B的度数(答案:50°或65°或80°)
张老师启发同学们进行变式,小敏编了如下一题:
变式:等腰△ABC中,∠A=70°,求∠B的度数
(1)请你解答小敏编的变式题;
(2)解第(1)小题后小敏发现,∠A的度数不同得到∠B的度数的个数也可能不同.如果在等腰△ABC中,设∠A=x°,当∠B有三个不同的度数时,请你探索x的取值范围.
19.如图,在Rt△ABC中,CM平分∠ACB交AB于点M,过点M作MN∥BC交AC于点N,且MN平分∠AMC,若AN=1.
(1)求∠B的度数;
(2)求CN的长.
20.已知:如图,在△ABC中,∠1=∠2,DE∥AC,求证:△ADE是等腰三角形.
21.如图,△ABC中,AB=AC,AD是BC边上的中线,CE⊥AB于点E.求证:∠CAD=∠BCE.
22.已知:如图,在等腰△ABC中,AB=AC,∠BAC=80°,AD平分∠BAC,且AD=AE;求∠EDC的度数.
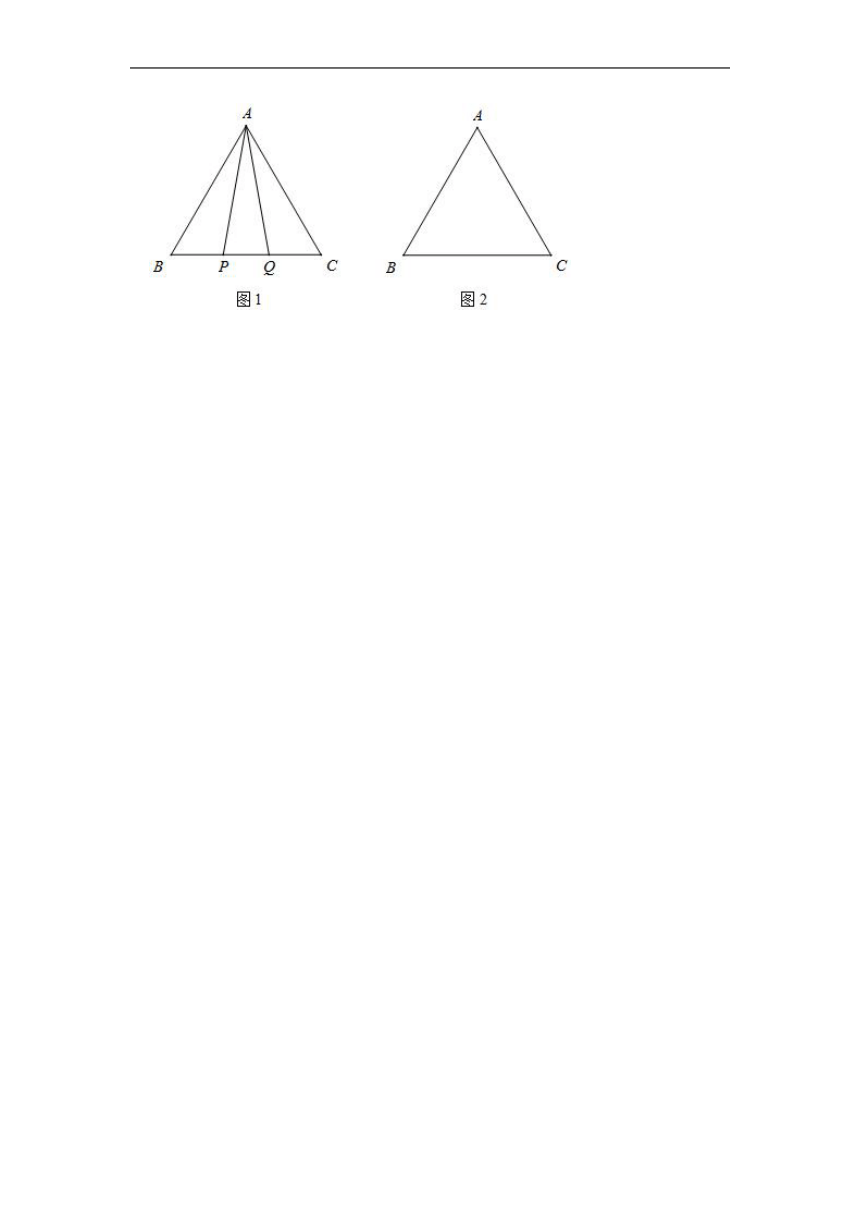
23.在等边△ABC中,
(1)如图1,P,Q是BC边上两点,AP=AQ,∠BAP=20°,求∠AQB的度数;
(2)点P,Q是BC边上的两个动点(不与B,C重合),点P在点Q的左侧,且AP=AQ,点Q关于直线AC的对称点为M,连接AM,PM.
①依题意将图2补全;
②求证:PA=PM.
参考答案
一.选择题(共12小题)
1.解:∵AB=AC=2,∠B=60°,
∴∠ADB=90°,
∴AD=AB=,
故选:C.
2.解:由题可得,CA=CD,BA=BD,
∴CB是AD的垂直平分线,
即CE垂直平分AD,故A选项正确;
∴∠CAD=∠CDA,∠CEA=∠CED,
∴∠ACE=∠DCE,
即CE平分∠ACD,故B选项正确;
∵DB=AB,
∴△ABD是等腰三角形,故C选项正确;
∵AD与AC不一定相等,
∴△ACD不一定是等边三角形,故D选项错误;
故选:D.
3.解:由翻折可知:△BED≌△BCD,
∴∠EBD=∠CBD,∠E=∠C=90°
∵△EDF是等腰三角形,
∴∠EFD=∠AFB=∠ABF=45°,
∴∠CBF=45°,
∴∠CBD=∠CBE=22.5°,
∴∠BDC=67.5°,
故选:C.
4.解:∵∠ABC、∠ACB的平分线相交于点E,
∴∠MBE=∠EBC,∠ECN=∠ECB,
∵MN∥BC,
∴∠EBC=∠MEB,∠NEC=∠ECB,
∴∠MBE=∠MEB,∠NEC=∠ECN,
∴BM=ME,EN=CN,
∴MN=ME+EN,
即MN=BM+CN.
∵BM+CN=8,
∴MN=8,
故选:C.
5.解:∵等边△ABC的边长为2,AD是BC边上的高,
∴∠ADC=90°,BD=CD=BC=1,
∴AD=,
故选:C.
6.解:2是腰长时,三角形的三边分别为2、2、4,
∵2+2=4,
∴不能组成三角形,
2是底边时,三角形的三边分别为2、4、4,
能组成三角形,
周长=2+4+4=10.
故选:A.
7.解:当腰为6时,另一腰也为6,则底为20﹣2×6=8,
∵6+6=12>8,
∴三边能构成三角形.
当底为6时,腰为(20﹣6)÷2=7,
∵7+7>6,
∴三边能构成三角形.
故选:C.
8.解:∵AD=AC,点E是CD中点,
∴AE⊥CD,
∴∠AEC=90°,
∴∠C=90°﹣∠CAE=74°,
∵AD=AC,
∴∠ADC=∠C=74°,
∵AD=BD,
∴2∠B=∠ADC=74°,
∴∠B=37°,
故选:C.
9.解:∵AB=AC,
∴∠B=∠C=30°,
∴∠BAC=180°﹣30°﹣30°=120°,
∵DE垂直平分线段AC,
∴EA=EC,
∴∠EAD=∠C=30°,
∴∠BAE=∠BAC﹣∠EAD=90°.
故选:C.
10.解:∵AB=AC,AD是△ABC的中线,
∴∠BAD=∠CAD=20°,∠ABC=∠ACB,
∴∠ACB==70°,
∵CE是△ABC的角平分线,
∴∠ACE=∠ACB=35°,
故选:B.
11.解:当腰为4时,另一腰也为4,则底为18﹣2×4=10,
∵4+4=8<10,
∴这样的三边不能构成三角形.
当底为4时,腰为(18﹣4)÷2=7,
∵0<7<7+4=11,
∴以4,7,7为边能构成三角形
∴其它两边长分别为7,7.
故选:B.
12.解:设顶角的度数为x,则底角的度数为(x﹣30°).
根据题意,得x+2(x﹣30°)=180°,
解得x=80°.
故选:C.
二.填空题
13.解:∵AB=AC,∠B=50°,
∴∠C=∠B=50°,
∴∠A=180°﹣2×50°=80°.
故答案为:80.
14.解:∵BD是∠ABC的平分线,
∴∠EBD=∠DBC,
∵过点D作BC的平行线交AB于点E,
∴∠EDB=∠EBD,
∴BE=ED,
∴∠EDB=∠EBD=(180°﹣∠BED),
同理∠FDC=(180°﹣∠DFC),
∴∠BDC=180°﹣∠BDE﹣∠CDF=180°﹣(180°﹣∠BED)﹣(180°﹣∠DFC)=(∠BED+∠CFD)=120°,
故答案为:120°
15.解:△BCP为等腰三角形时,
当点P在边AC上时,CP=CB,
∵CP=6cm,此时t=6÷2=3(秒);
当点P在边AB上时.
①如图1,CP=CB,
作AB边上的高CD,
∵AC×BC=AB×CD.
∴CD==4.8,
在Rt△CDP中,根据勾股定理得,DP=3.6,
∴BP=2DP=7.2,
∴AP=2.8,
∴t=(AC+AP)÷2=(8+2.8)÷2=5.4(秒)
②BC=BP,
∴BP=6cm,CA+AP=8+10﹣6=12(cm),
∴t=12÷2=6(秒);
③PB=PC,
∴点P在BC的垂直平分线与AB的交点处,即在AB的中点,
此时CA+AP=8+5=13(cm),
t=13÷2=6.5(秒);
综上可知,当t=3秒或5.4秒或6秒或6.5秒时,△BCP为等腰三角形.
故答案为:3秒或5.4秒或6秒或6.5秒.
16.解:∵AC=AD,∠DAC=84°,
∴∠ADC=∠C=48°,
∵AD=DB,
∴∠B=∠BAD,
∴∠B=∠ADC=24°.
故答案为:24.
三.解答题
17.解:(1)∵∠BAD=10°,∠DAE=30°,
∴∠BAC=∠BAD+∠DAE=40°,
∵AB=AC,
∴∠B=∠C=(180°﹣∠BAC)=70°.
∵AD=AE,∠DAE=30°,
∴∠ADE=∠AED=(180°﹣∠DAE)=75°.
∵∠B=70°,∠BAD=10°,
∴∠ADC=∠B+∠BAD=80°,
∴∠EDC=∠ADC﹣∠ADE=5°.
故答案为5;
(2)∵AB=AC,∠ABC=60°,
∴∠BAC=60°,
∵AD=AE,∠ADE=70°,
∴∠DAE=180°﹣2∠ADE=40°,
∴∠BAD=60°﹣40°=20°,
∴∠ADC=∠BAD+∠ABD=60°+20°=80°,
∴∠CDE=∠ADC﹣∠ADE=10°,
故答案为:20,10;
(3)猜想:α=2β.理由如下:
设∠B=x,∠AED=y,
∵AB=AC,AD=AE,
∴∠C=∠B=x,∠ADE=∠AED=y.
∵∠AED=∠CDE+∠C,
∴y=β+x,
∵∠ADC=∠BAD+∠B=∠ADE+∠CDE,
∴α+x=y+β=β+x+β,
∴α=2β.
18.解:(1)若∠A为顶角,则∠B=(180°﹣∠A)÷2=55°;
若∠A为底角,∠B为顶角,则∠B=180°﹣2×70°=40°;
若∠A为底角,∠B为底角,则∠B=70°;
故∠B=55°或40°或70°;
(2)分两种情况:
①当90≤x<180时,∠A只能为顶角,
∴∠B的度数只有一个;
②当0<x<90时,
若∠A为顶角,则∠B=()°;
若∠A为底角,∠B为顶角,则∠B=(180﹣2x)°;
若∠A为底角,∠B为底角,则∠B=x°.
当≠180﹣2x且180﹣2x≠x且≠x,
即x≠60时,∠B有三个不同的度数.
综上所述,可知当0<x<90且x≠60时,∠B有三个不同的度数.
19.解:(1)∵CM平分∠ACB,MN平分∠AMC,
∴∠ACM=∠BCM,∠AMN=∠CMN,
又∵MN∥BC,
∴∠AMN=∠B,∠CMN=∠BCM,
∴∠B=∠BCM=∠ACM,
∵∠A=90°,
∴∠B=×90°=30°;
(2)由(1)得,∠AMN=∠B=30°,∠MCN=∠CMN,∠A=90°,
∴MN=2AN=2,MN=CN,
∴CN=2.
20.证明:∵DE∥AC,
∴∠ADE=∠2,
∵∠1=∠2,
∴∠ADE=∠1,
∴EA=ED,
即△ADE是等腰三角形.
21.证明:∵AB=AC,BD=CD(已知),
∴∠B=∠ACB(等边对等角),AD⊥BC(等腰三角形底边上的中线与底边上的高互相重合).
又∵CE⊥AB(已知),
∴∠CAD+∠ACB=90°,∠BCE+∠B=90°(直角三角形的两个锐角互余).
∴∠CAD=∠BCE(等角的余角相等).
22.解:∵AB=AC,AD平分∠BAC,
∴AD⊥BC,∠ADC=90°,
∵∠BAC=80°,
∴∠DAE=∠BAC=40°,
∵AD=AE,
∴∠ADE=70°,
∴∠EDC=90°﹣70°=20°.
23.解:(1)∵△ABC为等边三角形
∴∠B=60°
∴∠APC=∠BAP+∠B=80°
∵AP=AQ
∴∠AQB=∠APC=80°,
(2)①补全图形如图所示,
②证明:过点A作AH⊥BC于点H,如图.
由△ABC为等边三角形,
∴∠B=∠C=60°,
∵AP=AQ,
∴∠APQ=∠AQP,
∴∠APQ﹣∠B=∠AQP﹣∠C,
即∠PAB=∠QAC,
∵点Q,M关于直线AC对称,
∴∠QAC=∠MAC,AQ=AM
∴∠MAC+∠PAC=∠PAB+∠PAC=60°,
∵AP=AM,
∴△APM为等边三角形
∴PA=PM.
一.选择题
1.如图,在△ABC中,AB=AC=2,∠B=60°,AD平分∠BAC,则AD等于( )
A.1 B. C. D.1.5
2.如图,在钝角三角形ABC中,∠ABC为钝角,以点B为圆心,AB长为半径画弧;再以点C为圆心,AC长为半径画弧;两弧交于点D,连接AD,CB的延长线交AD于点E.下列结论错误的是( )
A.CE垂直平分AD B.CE平分∠ACD
C.△ABD是等腰三角形 D.△ACD是等边三角形
3.如图,把一张长方形纸片沿对角线折叠,若△EDF是等腰三角形,则∠BDC=( )
A.45° B.60° C.67.5° D.75°
4.如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=8,则线段MN的长为( )
A.6 B.7 C.8 D.9
5.如图,等边△ABC的边长为2,AD是BC边上的高,则高AD的长为( )
A.1 B. C. D.2
6.一个等腰三角形的两边长分别是2、4,那么它的周长是( )
A.10 B.8 C.10或8 D.不能确定
7.已知等腰三角形的周长是20,其中一边长为6,则其它两边的长度分别是( )
A.6和8 B.7和7 C.6和8或7和7 D.3和11
8.如图,在△ABC中,点D在BC边上,BD=AD=AC,E为CD的中点,若∠CAE=16°,则∠B的大小为( )
A.32° B.36° C.37° D.74°
9.如图,△ABC中,AB=AC,∠B=30°,点D是AC的中点,过点D作DE⊥AC交BC于点E,连接EA.则∠BAE的度数为( )
A.30° B.80° C.90° D.110°
10.如图,在△ABC中,AB=AC,AD、CE分别是△ABC的中线和角平分线.若∠CAD=20°,则∠ACE的度数是( )
A.20° B.35° C.40° D.70°
11.等腰三角形周长为18,其中一边长为4,则其它两边长分别为( )
A.4,10 B.7,7 C.4,10或7,7 D.无法确定
12.等腰三角形的顶角比每个底角大30°,则这个等腰三角形的顶角是( )
A.40° B.50° C.80° D.85°
二.填空题
13.已知等腰△ABC中,AB=AC,∠B=50°,则∠A= 度.
14.如图,在△ABC中,∠ABC的平分线与∠ACB的平分线交于点D,过点D作BC的平行线交AB于点E,交AC于点F,已知∠BED+∠CFD=240°,则∠BDC= .
15.在△ABC中,∠C=90°,AC=8cm,BC=6cm.动点P从点C开始按C→A→B→C的路径绕△ABC的边运动一周,速度为每秒2cm,运动的时间为t秒.则△BCP为等腰三角形时t的值是 .
16.如图,△ABC中,D是BC上一点,AC=AD=BD,若∠DAC=84°,则∠B= 度.
三.解答题
17.已知△ABC,AB=AC,D为BC上一点,E为AC上一点,AD=AE.
(1)如果∠BAD=10°,∠DAE=30°,那么∠EDC= °.
(2)如果∠ABC=60°,∠ADE=70°,那么∠BAD= °,∠CDE= °.
(3)设∠BAD=α,∠CDE=β猜想α,β之间的关系式,并说明理由.
18.数学课上,张老师举了下面的例题:
例1:等腰△ABC中,∠A=100°,求∠B的度数(答案:40°)
例2:等腰△ABC中,∠A=50°,求∠B的度数(答案:50°或65°或80°)
张老师启发同学们进行变式,小敏编了如下一题:
变式:等腰△ABC中,∠A=70°,求∠B的度数
(1)请你解答小敏编的变式题;
(2)解第(1)小题后小敏发现,∠A的度数不同得到∠B的度数的个数也可能不同.如果在等腰△ABC中,设∠A=x°,当∠B有三个不同的度数时,请你探索x的取值范围.
19.如图,在Rt△ABC中,CM平分∠ACB交AB于点M,过点M作MN∥BC交AC于点N,且MN平分∠AMC,若AN=1.
(1)求∠B的度数;
(2)求CN的长.
20.已知:如图,在△ABC中,∠1=∠2,DE∥AC,求证:△ADE是等腰三角形.
21.如图,△ABC中,AB=AC,AD是BC边上的中线,CE⊥AB于点E.求证:∠CAD=∠BCE.
22.已知:如图,在等腰△ABC中,AB=AC,∠BAC=80°,AD平分∠BAC,且AD=AE;求∠EDC的度数.
23.在等边△ABC中,
(1)如图1,P,Q是BC边上两点,AP=AQ,∠BAP=20°,求∠AQB的度数;
(2)点P,Q是BC边上的两个动点(不与B,C重合),点P在点Q的左侧,且AP=AQ,点Q关于直线AC的对称点为M,连接AM,PM.
①依题意将图2补全;
②求证:PA=PM.
参考答案
一.选择题(共12小题)
1.解:∵AB=AC=2,∠B=60°,
∴∠ADB=90°,
∴AD=AB=,
故选:C.
2.解:由题可得,CA=CD,BA=BD,
∴CB是AD的垂直平分线,
即CE垂直平分AD,故A选项正确;
∴∠CAD=∠CDA,∠CEA=∠CED,
∴∠ACE=∠DCE,
即CE平分∠ACD,故B选项正确;
∵DB=AB,
∴△ABD是等腰三角形,故C选项正确;
∵AD与AC不一定相等,
∴△ACD不一定是等边三角形,故D选项错误;
故选:D.
3.解:由翻折可知:△BED≌△BCD,
∴∠EBD=∠CBD,∠E=∠C=90°
∵△EDF是等腰三角形,
∴∠EFD=∠AFB=∠ABF=45°,
∴∠CBF=45°,
∴∠CBD=∠CBE=22.5°,
∴∠BDC=67.5°,
故选:C.
4.解:∵∠ABC、∠ACB的平分线相交于点E,
∴∠MBE=∠EBC,∠ECN=∠ECB,
∵MN∥BC,
∴∠EBC=∠MEB,∠NEC=∠ECB,
∴∠MBE=∠MEB,∠NEC=∠ECN,
∴BM=ME,EN=CN,
∴MN=ME+EN,
即MN=BM+CN.
∵BM+CN=8,
∴MN=8,
故选:C.
5.解:∵等边△ABC的边长为2,AD是BC边上的高,
∴∠ADC=90°,BD=CD=BC=1,
∴AD=,
故选:C.
6.解:2是腰长时,三角形的三边分别为2、2、4,
∵2+2=4,
∴不能组成三角形,
2是底边时,三角形的三边分别为2、4、4,
能组成三角形,
周长=2+4+4=10.
故选:A.
7.解:当腰为6时,另一腰也为6,则底为20﹣2×6=8,
∵6+6=12>8,
∴三边能构成三角形.
当底为6时,腰为(20﹣6)÷2=7,
∵7+7>6,
∴三边能构成三角形.
故选:C.
8.解:∵AD=AC,点E是CD中点,
∴AE⊥CD,
∴∠AEC=90°,
∴∠C=90°﹣∠CAE=74°,
∵AD=AC,
∴∠ADC=∠C=74°,
∵AD=BD,
∴2∠B=∠ADC=74°,
∴∠B=37°,
故选:C.
9.解:∵AB=AC,
∴∠B=∠C=30°,
∴∠BAC=180°﹣30°﹣30°=120°,
∵DE垂直平分线段AC,
∴EA=EC,
∴∠EAD=∠C=30°,
∴∠BAE=∠BAC﹣∠EAD=90°.
故选:C.
10.解:∵AB=AC,AD是△ABC的中线,
∴∠BAD=∠CAD=20°,∠ABC=∠ACB,
∴∠ACB==70°,
∵CE是△ABC的角平分线,
∴∠ACE=∠ACB=35°,
故选:B.
11.解:当腰为4时,另一腰也为4,则底为18﹣2×4=10,
∵4+4=8<10,
∴这样的三边不能构成三角形.
当底为4时,腰为(18﹣4)÷2=7,
∵0<7<7+4=11,
∴以4,7,7为边能构成三角形
∴其它两边长分别为7,7.
故选:B.
12.解:设顶角的度数为x,则底角的度数为(x﹣30°).
根据题意,得x+2(x﹣30°)=180°,
解得x=80°.
故选:C.
二.填空题
13.解:∵AB=AC,∠B=50°,
∴∠C=∠B=50°,
∴∠A=180°﹣2×50°=80°.
故答案为:80.
14.解:∵BD是∠ABC的平分线,
∴∠EBD=∠DBC,
∵过点D作BC的平行线交AB于点E,
∴∠EDB=∠EBD,
∴BE=ED,
∴∠EDB=∠EBD=(180°﹣∠BED),
同理∠FDC=(180°﹣∠DFC),
∴∠BDC=180°﹣∠BDE﹣∠CDF=180°﹣(180°﹣∠BED)﹣(180°﹣∠DFC)=(∠BED+∠CFD)=120°,
故答案为:120°
15.解:△BCP为等腰三角形时,
当点P在边AC上时,CP=CB,
∵CP=6cm,此时t=6÷2=3(秒);
当点P在边AB上时.
①如图1,CP=CB,
作AB边上的高CD,
∵AC×BC=AB×CD.
∴CD==4.8,
在Rt△CDP中,根据勾股定理得,DP=3.6,
∴BP=2DP=7.2,
∴AP=2.8,
∴t=(AC+AP)÷2=(8+2.8)÷2=5.4(秒)
②BC=BP,
∴BP=6cm,CA+AP=8+10﹣6=12(cm),
∴t=12÷2=6(秒);
③PB=PC,
∴点P在BC的垂直平分线与AB的交点处,即在AB的中点,
此时CA+AP=8+5=13(cm),
t=13÷2=6.5(秒);
综上可知,当t=3秒或5.4秒或6秒或6.5秒时,△BCP为等腰三角形.
故答案为:3秒或5.4秒或6秒或6.5秒.
16.解:∵AC=AD,∠DAC=84°,
∴∠ADC=∠C=48°,
∵AD=DB,
∴∠B=∠BAD,
∴∠B=∠ADC=24°.
故答案为:24.
三.解答题
17.解:(1)∵∠BAD=10°,∠DAE=30°,
∴∠BAC=∠BAD+∠DAE=40°,
∵AB=AC,
∴∠B=∠C=(180°﹣∠BAC)=70°.
∵AD=AE,∠DAE=30°,
∴∠ADE=∠AED=(180°﹣∠DAE)=75°.
∵∠B=70°,∠BAD=10°,
∴∠ADC=∠B+∠BAD=80°,
∴∠EDC=∠ADC﹣∠ADE=5°.
故答案为5;
(2)∵AB=AC,∠ABC=60°,
∴∠BAC=60°,
∵AD=AE,∠ADE=70°,
∴∠DAE=180°﹣2∠ADE=40°,
∴∠BAD=60°﹣40°=20°,
∴∠ADC=∠BAD+∠ABD=60°+20°=80°,
∴∠CDE=∠ADC﹣∠ADE=10°,
故答案为:20,10;
(3)猜想:α=2β.理由如下:
设∠B=x,∠AED=y,
∵AB=AC,AD=AE,
∴∠C=∠B=x,∠ADE=∠AED=y.
∵∠AED=∠CDE+∠C,
∴y=β+x,
∵∠ADC=∠BAD+∠B=∠ADE+∠CDE,
∴α+x=y+β=β+x+β,
∴α=2β.
18.解:(1)若∠A为顶角,则∠B=(180°﹣∠A)÷2=55°;
若∠A为底角,∠B为顶角,则∠B=180°﹣2×70°=40°;
若∠A为底角,∠B为底角,则∠B=70°;
故∠B=55°或40°或70°;
(2)分两种情况:
①当90≤x<180时,∠A只能为顶角,
∴∠B的度数只有一个;
②当0<x<90时,
若∠A为顶角,则∠B=()°;
若∠A为底角,∠B为顶角,则∠B=(180﹣2x)°;
若∠A为底角,∠B为底角,则∠B=x°.
当≠180﹣2x且180﹣2x≠x且≠x,
即x≠60时,∠B有三个不同的度数.
综上所述,可知当0<x<90且x≠60时,∠B有三个不同的度数.
19.解:(1)∵CM平分∠ACB,MN平分∠AMC,
∴∠ACM=∠BCM,∠AMN=∠CMN,
又∵MN∥BC,
∴∠AMN=∠B,∠CMN=∠BCM,
∴∠B=∠BCM=∠ACM,
∵∠A=90°,
∴∠B=×90°=30°;
(2)由(1)得,∠AMN=∠B=30°,∠MCN=∠CMN,∠A=90°,
∴MN=2AN=2,MN=CN,
∴CN=2.
20.证明:∵DE∥AC,
∴∠ADE=∠2,
∵∠1=∠2,
∴∠ADE=∠1,
∴EA=ED,
即△ADE是等腰三角形.
21.证明:∵AB=AC,BD=CD(已知),
∴∠B=∠ACB(等边对等角),AD⊥BC(等腰三角形底边上的中线与底边上的高互相重合).
又∵CE⊥AB(已知),
∴∠CAD+∠ACB=90°,∠BCE+∠B=90°(直角三角形的两个锐角互余).
∴∠CAD=∠BCE(等角的余角相等).
22.解:∵AB=AC,AD平分∠BAC,
∴AD⊥BC,∠ADC=90°,
∵∠BAC=80°,
∴∠DAE=∠BAC=40°,
∵AD=AE,
∴∠ADE=70°,
∴∠EDC=90°﹣70°=20°.
23.解:(1)∵△ABC为等边三角形
∴∠B=60°
∴∠APC=∠BAP+∠B=80°
∵AP=AQ
∴∠AQB=∠APC=80°,
(2)①补全图形如图所示,
②证明:过点A作AH⊥BC于点H,如图.
由△ABC为等边三角形,
∴∠B=∠C=60°,
∵AP=AQ,
∴∠APQ=∠AQP,
∴∠APQ﹣∠B=∠AQP﹣∠C,
即∠PAB=∠QAC,
∵点Q,M关于直线AC对称,
∴∠QAC=∠MAC,AQ=AM
∴∠MAC+∠PAC=∠PAB+∠PAC=60°,
∵AP=AM,
∴△APM为等边三角形
∴PA=PM.
