2022-2023学年鲁教版(五四制)九年级数学上册 2.6.2 方向角在测量中的应用 同步练习 (word版 含答案)
文档属性
| 名称 | 2022-2023学年鲁教版(五四制)九年级数学上册 2.6.2 方向角在测量中的应用 同步练习 (word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 417.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-24 15:28:39 | ||
图片预览


文档简介
方向角在测量中的应用
同步精练
一、选择题(共10小题,每小题4分,共40分)
1. 如图,一艘轮船位于灯塔P的南偏东60°方向,距离灯塔50海里的A处,它沿正北方向航行一段时间后,到达位于灯塔的北偏东45°方向上的B处,此时B处与灯塔P的距离为( )海里(结果保留根号).
A. 25 B. 25 C. 25 D. 25
2. 如图,海中有一个小岛A,一艘轮船由西向东航行,在B点测得小岛A在北偏东60°方向上;航行12 n mile到达C点,这时测得小岛A在北偏东30°方向上.小岛A到航线BC的距离是( )n mile(≈1.73,结果用四舍五入法精确到0.1 n mile).
A. 10.4 B. 11.2 C. 12.1 D. 15.6
3. 在数学活动课上,九(1)班数学兴趣小组的同学们要测量某公园人工湖亭子A与它正东方向的亭子B之间的距离.现测得亭子A位于点P北偏西30°方向,亭子B位于点P北偏东α方向,测得点P与亭子A之间的距离为200米.则亭子A与亭子B之间的距离为( )
A.100+米 B.100+100·sin α米
C.100+米 D.100+100·tan α米
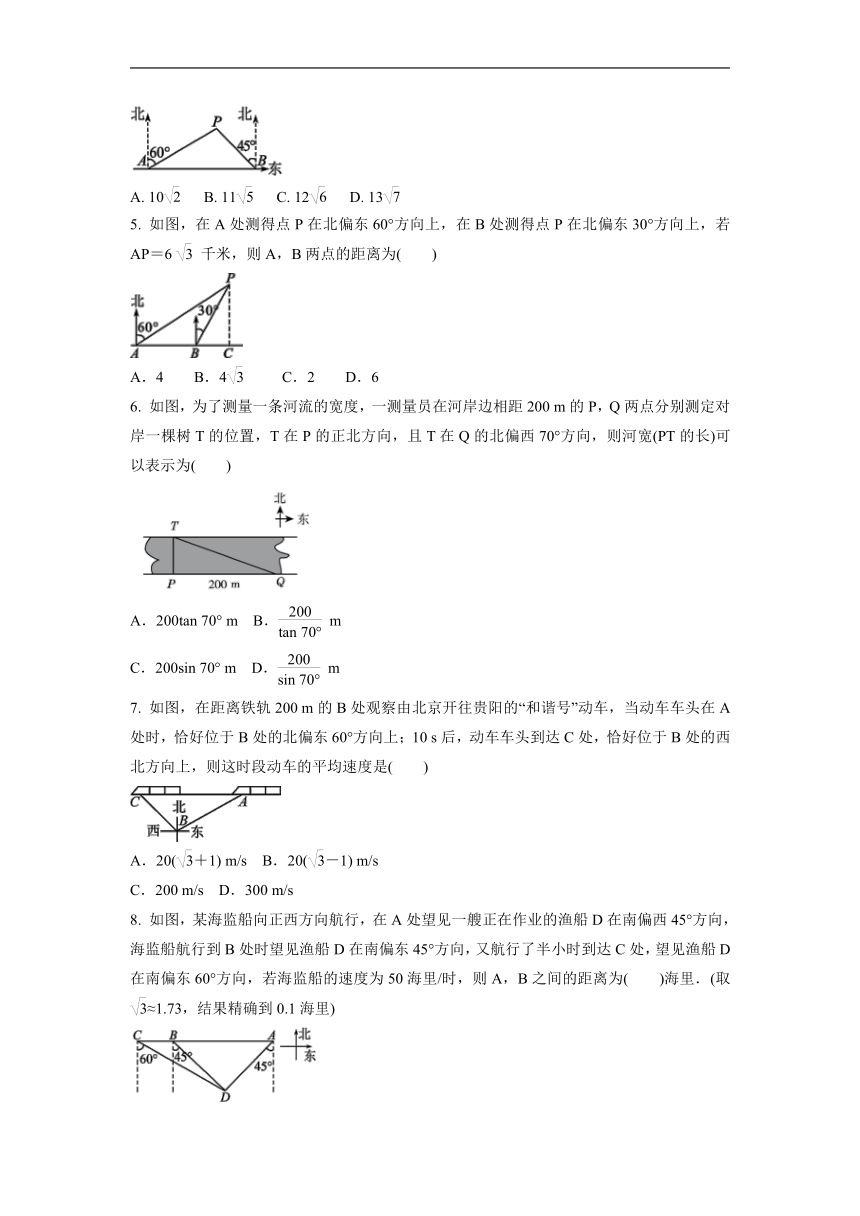
4. 如图,在东西方向的海岸线上有A,B两个港口,甲货船从A港沿北偏东60°的方向以20海里/时的速度出发,同时乙货船从B港沿西北方向出发,2小时后相遇在点P处,则乙货船每小时航行( )海里.
A. 10 B. 11 C. 12 D. 13
5. 如图,在A处测得点P在北偏东60°方向上,在B处测得点P在北偏东30°方向上,若AP=6千米,则A,B两点的距离为( )
A.4 B.4 C.2 D.6
6. 如图,为了测量一条河流的宽度,一测量员在河岸边相距200 m的P,Q两点分别测定对岸一棵树T的位置,T在P的正北方向,且T在Q的北偏西70°方向,则河宽(PT的长)可以表示为( )
A.200tan 70° m B. m
C.200sin 70° m D. m
7. 如图,在距离铁轨200 m的B处观察由北京开往贵阳的“和谐号”动车,当动车车头在A处时,恰好位于B处的北偏东60°方向上;10 s后,动车车头到达C处,恰好位于B处的西北方向上,则这时段动车的平均速度是( )
A.20(+1) m/s B.20(-1) m/s
C.200 m/s D.300 m/s
8. 如图,某海监船向正西方向航行,在A处望见一艘正在作业的渔船D在南偏西45°方向,海监船航行到B处时望见渔船D在南偏东45°方向,又航行了半小时到达C处,望见渔船D在南偏东60°方向,若海监船的速度为50海里/时,则A,B之间的距离为( )海里.(取≈1.73,结果精确到0.1海里)
A.65.2 B.66.8 C.68.3 D69.1
9. 如图,在某监测点B处望见一艘正在作业的渔船在南偏西15°方向的A处,若渔船沿北偏西75°方向以40海里/小时的速度航行,航行半小时后到达C处,在C处观测到B在C的北偏东60°方向上,则B,C之间的距离为( )
A.20海里 B.10海里
C.20海里 D.30海里
10. 如图,一艘船由A港沿北偏东65°方向航行30km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向,则A,C两港之间的距离为( )
A.(30+30)km B.(30+10)km
C.(10+30)km D.30 km
二.填空题(共6小题,每小题4分,共24分)
11. 如图,小雅家(图中点O处)门前有一条东西走向的公路,经测得有一水塔(图中点A处)在距她家北偏东60°方向的500米处,那么水塔所在的位置到公路的距离AB是________.
12. 如图,一渔船以32海里/时的速度向正北航行,在A处看到灯塔S在渔船的北偏东30°,半小时后航行到B处看到灯塔S在船的北偏东60°,若渔船继续向正北航行到C处时,此时渔船在灯塔S的正西方向,此时灯塔S与渔船的距离____海里.
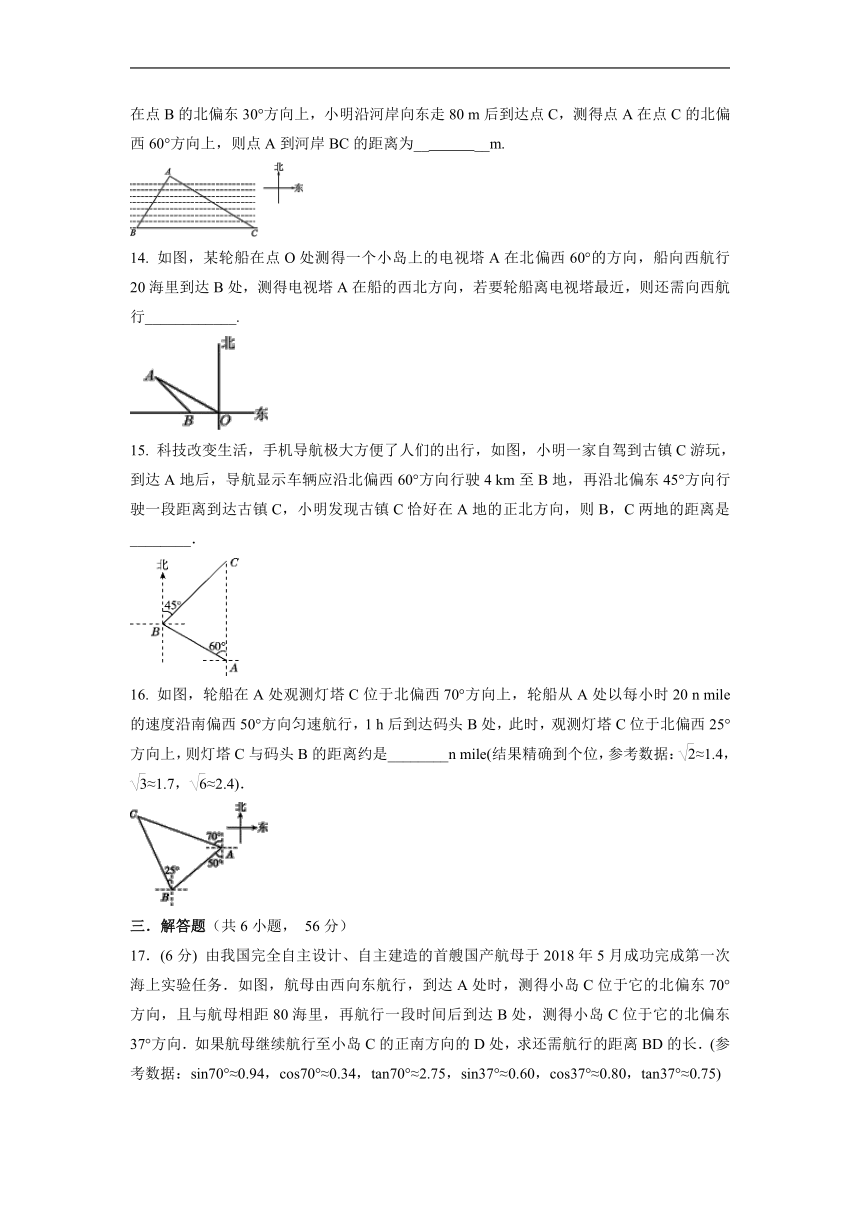
13. 如图,已知一条东西走向的河流,在河流对岸有一点A,小明在岸边点B处测得点A在点B的北偏东30°方向上,小明沿河岸向东走80 m后到达点C,测得点A在点C的北偏西60°方向上,则点A到河岸BC的距离为__ __m.
14. 如图,某轮船在点O处测得一个小岛上的电视塔A在北偏西60°的方向,船向西航行20海里到达B处,测得电视塔A在船的西北方向,若要轮船离电视塔最近,则还需向西航行____________.
15. 科技改变生活,手机导航极大方便了人们的出行,如图,小明一家自驾到古镇C游玩,到达A地后,导航显示车辆应沿北偏西60°方向行驶4 km至B地,再沿北偏东45°方向行驶一段距离到达古镇C,小明发现古镇C恰好在A地的正北方向,则B,C两地的距离是________.
16. 如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20 n mile的速度沿南偏西50°方向匀速航行,1 h后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离约是________n mile(结果精确到个位,参考数据:≈1.4,≈1.7,≈2.4).
三.解答题(共6小题, 56分)
17.(6分) 由我国完全自主设计、自主建造的首艘国产航母于2018年5月成功完成第一次海上实验任务.如图,航母由西向东航行,到达A处时,测得小岛C位于它的北偏东70°方向,且与航母相距80海里,再航行一段时间后到达B处,测得小岛C位于它的北偏东37°方向.如果航母继续航行至小岛C的正南方向的D处,求还需航行的距离BD的长.(参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
18.(8分) 由我国完全自主设计、自主建造的首艘国产航母于2018年5月成功完成第一次海上试验任务.如图,航母由西向东航行,到达A处时,测得小岛C位于它的北偏东70°方向,且与航母相距80海里,再航行一段时间后到达B处,测得小岛C位于它的北偏东37°方向.如果航母继续航行至小岛C的正南方向的D处,求还需航行的距离BD的长.(参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75,sin37°≈0.6,cos37°≈0.80,tan37°≈0.75)
19.(8分) 如图,一艘轮船位于灯塔C的北偏东45°方向,距离灯塔100海里的A处,它沿正南方向航行一段时间后,到达位于灯塔C的南偏东30°方向上的B处,求此时轮船距灯塔的距离.(参考数据:≈1.414,≈1.732,结果取整数)
20.(10分) 为了保证端午龙舟赛在我市汉江水域顺利举办,某部门工作人员乘快艇到汉江水域考察水情,以每秒10米的速度沿平行于岸边的赛道AB由西向东行驶.在A处测得岸边一建筑物P在北偏东30°方向上,继续行驶40秒到达B处时,测得建筑物P在北偏西60°方向上,如图所示,求建筑物P到赛道AB的距离.(结果保留根号)
21.(12分) 如图,海中一小岛上有一个观测点A,某天上午9:00观测到某渔船在观测点A的西南方向上的B处跟踪鱼群由南向北匀速航行.当天上午9:30观测到该渔船在观测点A的北偏西60°方向上的C处.若该渔船的速度为30 n mile/h,在此航行过程中,该渔船从B处开始航行多少小时,离观测点A的距离最近?(计算结果用根号表示,不取近似值)
22.(12分) 如图,一艘渔船位于小岛B的北偏东30°,距离小岛40 n mile的点A处,它沿着点A的南偏东15°的方向航行.
(1)渔船航行多远距离小岛B最近?(结果保留根号)
(2)渔船到达距离小岛B最近点后,按原航向继续航行20 n mile到点C处时突然发生事故,渔船马上向小岛B上的救援队求救,问救援队从B处出发沿着哪个方向航行到达事故地点航程最短,最短航程是多少?(结果保留根号)
参考答案
1-5DADAB 6-10BACCB
11.250米
12. 8
13. 20
14. 10(+1)海里
16. 2 km.
16. 24
17. 解:由题意,得∠ACD=70°,∠BCD=37°,AC=80海里,∴在Rt△ACD中,CD=AC·cos∠ACD≈27.2(海里),在Rt△BCD中,BD=CD·tan∠BCD≈20.4(海里).∴还需航行的距离BD的长为20.4海里.
18. 解:由题意得:∠ACD=70°,∠BCD=37°,AC=80海里,在Rt△ACD中,CD=AC·cos∠ACD=27.2(海里),在Rt△BCD中,BD=CD·tan∠BCD=20.4(海里).答:还需航行的距离BD的长为20.4海里
19. 解:过C作CD⊥AB,在Rt△ACD中,∠A=45°,∴CD=AC·sin45°=50 (海里),在Rt△BCD中,∠B=30°,∴BC==100≈141海里,则此时轮船距灯塔的距离约为141海里
20. 解:如图,过点P作PC⊥AB于点C,由题意可知∠PAC=60°,∠PBC=30°,在Rt△PAC中,AC==PC,在Rt△PBC中,BC==PC,∵AB=AC+BC=PC+PC=10×40=400,∴PC=100,即建筑物P到赛道AB的距离为100米
21. 解:如图,过点A作AP⊥BC,垂足为P,设AP=x n mile.在Rt△APC中,∵∠APC=90°,∠PAC=90°-60°=30°,∴tan∠PAC==.∴CP=x n mile.在Rt△APB中,∵∠APB=90°,∠PAB=45°,∴BP=AP=x n mile.∵PC+BP=BC=30×=15(n mile),∴x+x=15.解得x=.∴PB= n mile.∴航行时间为÷30=(h).答:该渔船从B处开始航行 h,离观测点A的距离最近.
22. 解:(1)过B作BM⊥AC于M,如图.由题意可知∠BAM=45°.在Rt△ABM中,∵∠BAM=45°,AB=40 n mile,∴BM=AM=AB=20 n mile.∴渔船航行20 n mile距离小岛B最近.
(2)∵BM=20 n mile,MC=20 n mile,∴tan ∠MBC===,∴∠MBC=60°,∴∠CBG=180°-60°-45°-30°=45°.
同步精练
一、选择题(共10小题,每小题4分,共40分)
1. 如图,一艘轮船位于灯塔P的南偏东60°方向,距离灯塔50海里的A处,它沿正北方向航行一段时间后,到达位于灯塔的北偏东45°方向上的B处,此时B处与灯塔P的距离为( )海里(结果保留根号).
A. 25 B. 25 C. 25 D. 25
2. 如图,海中有一个小岛A,一艘轮船由西向东航行,在B点测得小岛A在北偏东60°方向上;航行12 n mile到达C点,这时测得小岛A在北偏东30°方向上.小岛A到航线BC的距离是( )n mile(≈1.73,结果用四舍五入法精确到0.1 n mile).
A. 10.4 B. 11.2 C. 12.1 D. 15.6
3. 在数学活动课上,九(1)班数学兴趣小组的同学们要测量某公园人工湖亭子A与它正东方向的亭子B之间的距离.现测得亭子A位于点P北偏西30°方向,亭子B位于点P北偏东α方向,测得点P与亭子A之间的距离为200米.则亭子A与亭子B之间的距离为( )
A.100+米 B.100+100·sin α米
C.100+米 D.100+100·tan α米
4. 如图,在东西方向的海岸线上有A,B两个港口,甲货船从A港沿北偏东60°的方向以20海里/时的速度出发,同时乙货船从B港沿西北方向出发,2小时后相遇在点P处,则乙货船每小时航行( )海里.
A. 10 B. 11 C. 12 D. 13
5. 如图,在A处测得点P在北偏东60°方向上,在B处测得点P在北偏东30°方向上,若AP=6千米,则A,B两点的距离为( )
A.4 B.4 C.2 D.6
6. 如图,为了测量一条河流的宽度,一测量员在河岸边相距200 m的P,Q两点分别测定对岸一棵树T的位置,T在P的正北方向,且T在Q的北偏西70°方向,则河宽(PT的长)可以表示为( )
A.200tan 70° m B. m
C.200sin 70° m D. m
7. 如图,在距离铁轨200 m的B处观察由北京开往贵阳的“和谐号”动车,当动车车头在A处时,恰好位于B处的北偏东60°方向上;10 s后,动车车头到达C处,恰好位于B处的西北方向上,则这时段动车的平均速度是( )
A.20(+1) m/s B.20(-1) m/s
C.200 m/s D.300 m/s
8. 如图,某海监船向正西方向航行,在A处望见一艘正在作业的渔船D在南偏西45°方向,海监船航行到B处时望见渔船D在南偏东45°方向,又航行了半小时到达C处,望见渔船D在南偏东60°方向,若海监船的速度为50海里/时,则A,B之间的距离为( )海里.(取≈1.73,结果精确到0.1海里)
A.65.2 B.66.8 C.68.3 D69.1
9. 如图,在某监测点B处望见一艘正在作业的渔船在南偏西15°方向的A处,若渔船沿北偏西75°方向以40海里/小时的速度航行,航行半小时后到达C处,在C处观测到B在C的北偏东60°方向上,则B,C之间的距离为( )
A.20海里 B.10海里
C.20海里 D.30海里
10. 如图,一艘船由A港沿北偏东65°方向航行30km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向,则A,C两港之间的距离为( )
A.(30+30)km B.(30+10)km
C.(10+30)km D.30 km
二.填空题(共6小题,每小题4分,共24分)
11. 如图,小雅家(图中点O处)门前有一条东西走向的公路,经测得有一水塔(图中点A处)在距她家北偏东60°方向的500米处,那么水塔所在的位置到公路的距离AB是________.
12. 如图,一渔船以32海里/时的速度向正北航行,在A处看到灯塔S在渔船的北偏东30°,半小时后航行到B处看到灯塔S在船的北偏东60°,若渔船继续向正北航行到C处时,此时渔船在灯塔S的正西方向,此时灯塔S与渔船的距离____海里.
13. 如图,已知一条东西走向的河流,在河流对岸有一点A,小明在岸边点B处测得点A在点B的北偏东30°方向上,小明沿河岸向东走80 m后到达点C,测得点A在点C的北偏西60°方向上,则点A到河岸BC的距离为__ __m.
14. 如图,某轮船在点O处测得一个小岛上的电视塔A在北偏西60°的方向,船向西航行20海里到达B处,测得电视塔A在船的西北方向,若要轮船离电视塔最近,则还需向西航行____________.
15. 科技改变生活,手机导航极大方便了人们的出行,如图,小明一家自驾到古镇C游玩,到达A地后,导航显示车辆应沿北偏西60°方向行驶4 km至B地,再沿北偏东45°方向行驶一段距离到达古镇C,小明发现古镇C恰好在A地的正北方向,则B,C两地的距离是________.
16. 如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20 n mile的速度沿南偏西50°方向匀速航行,1 h后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离约是________n mile(结果精确到个位,参考数据:≈1.4,≈1.7,≈2.4).
三.解答题(共6小题, 56分)
17.(6分) 由我国完全自主设计、自主建造的首艘国产航母于2018年5月成功完成第一次海上实验任务.如图,航母由西向东航行,到达A处时,测得小岛C位于它的北偏东70°方向,且与航母相距80海里,再航行一段时间后到达B处,测得小岛C位于它的北偏东37°方向.如果航母继续航行至小岛C的正南方向的D处,求还需航行的距离BD的长.(参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
18.(8分) 由我国完全自主设计、自主建造的首艘国产航母于2018年5月成功完成第一次海上试验任务.如图,航母由西向东航行,到达A处时,测得小岛C位于它的北偏东70°方向,且与航母相距80海里,再航行一段时间后到达B处,测得小岛C位于它的北偏东37°方向.如果航母继续航行至小岛C的正南方向的D处,求还需航行的距离BD的长.(参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75,sin37°≈0.6,cos37°≈0.80,tan37°≈0.75)
19.(8分) 如图,一艘轮船位于灯塔C的北偏东45°方向,距离灯塔100海里的A处,它沿正南方向航行一段时间后,到达位于灯塔C的南偏东30°方向上的B处,求此时轮船距灯塔的距离.(参考数据:≈1.414,≈1.732,结果取整数)
20.(10分) 为了保证端午龙舟赛在我市汉江水域顺利举办,某部门工作人员乘快艇到汉江水域考察水情,以每秒10米的速度沿平行于岸边的赛道AB由西向东行驶.在A处测得岸边一建筑物P在北偏东30°方向上,继续行驶40秒到达B处时,测得建筑物P在北偏西60°方向上,如图所示,求建筑物P到赛道AB的距离.(结果保留根号)
21.(12分) 如图,海中一小岛上有一个观测点A,某天上午9:00观测到某渔船在观测点A的西南方向上的B处跟踪鱼群由南向北匀速航行.当天上午9:30观测到该渔船在观测点A的北偏西60°方向上的C处.若该渔船的速度为30 n mile/h,在此航行过程中,该渔船从B处开始航行多少小时,离观测点A的距离最近?(计算结果用根号表示,不取近似值)
22.(12分) 如图,一艘渔船位于小岛B的北偏东30°,距离小岛40 n mile的点A处,它沿着点A的南偏东15°的方向航行.
(1)渔船航行多远距离小岛B最近?(结果保留根号)
(2)渔船到达距离小岛B最近点后,按原航向继续航行20 n mile到点C处时突然发生事故,渔船马上向小岛B上的救援队求救,问救援队从B处出发沿着哪个方向航行到达事故地点航程最短,最短航程是多少?(结果保留根号)
参考答案
1-5DADAB 6-10BACCB
11.250米
12. 8
13. 20
14. 10(+1)海里
16. 2 km.
16. 24
17. 解:由题意,得∠ACD=70°,∠BCD=37°,AC=80海里,∴在Rt△ACD中,CD=AC·cos∠ACD≈27.2(海里),在Rt△BCD中,BD=CD·tan∠BCD≈20.4(海里).∴还需航行的距离BD的长为20.4海里.
18. 解:由题意得:∠ACD=70°,∠BCD=37°,AC=80海里,在Rt△ACD中,CD=AC·cos∠ACD=27.2(海里),在Rt△BCD中,BD=CD·tan∠BCD=20.4(海里).答:还需航行的距离BD的长为20.4海里
19. 解:过C作CD⊥AB,在Rt△ACD中,∠A=45°,∴CD=AC·sin45°=50 (海里),在Rt△BCD中,∠B=30°,∴BC==100≈141海里,则此时轮船距灯塔的距离约为141海里
20. 解:如图,过点P作PC⊥AB于点C,由题意可知∠PAC=60°,∠PBC=30°,在Rt△PAC中,AC==PC,在Rt△PBC中,BC==PC,∵AB=AC+BC=PC+PC=10×40=400,∴PC=100,即建筑物P到赛道AB的距离为100米
21. 解:如图,过点A作AP⊥BC,垂足为P,设AP=x n mile.在Rt△APC中,∵∠APC=90°,∠PAC=90°-60°=30°,∴tan∠PAC==.∴CP=x n mile.在Rt△APB中,∵∠APB=90°,∠PAB=45°,∴BP=AP=x n mile.∵PC+BP=BC=30×=15(n mile),∴x+x=15.解得x=.∴PB= n mile.∴航行时间为÷30=(h).答:该渔船从B处开始航行 h,离观测点A的距离最近.
22. 解:(1)过B作BM⊥AC于M,如图.由题意可知∠BAM=45°.在Rt△ABM中,∵∠BAM=45°,AB=40 n mile,∴BM=AM=AB=20 n mile.∴渔船航行20 n mile距离小岛B最近.
(2)∵BM=20 n mile,MC=20 n mile,∴tan ∠MBC===,∴∠MBC=60°,∴∠CBG=180°-60°-45°-30°=45°.
