人教版八年级上册11.1.1三角形的边 课件(共18张PPT)
文档属性
| 名称 | 人教版八年级上册11.1.1三角形的边 课件(共18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-24 07:34:36 | ||
图片预览



文档简介
(共18张PPT)
导入新课
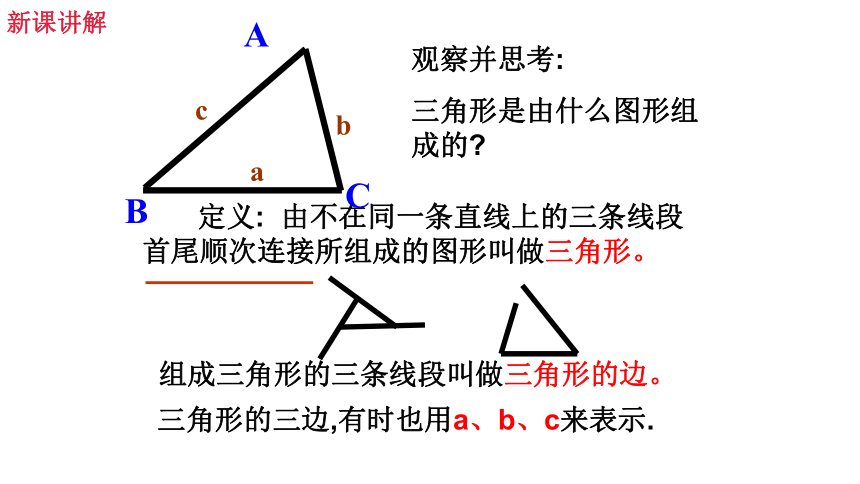
定义: 由不在同一条直线上的三条线段 首尾顺次连接所组成的图形叫做三角形。
A
B
C
观察并思考:
三角形是由什么图形组成的
组成三角形的三条线段叫做三角形的边。
三角形的三边,有时也用a、b、c来表示.
a
b
c
新课讲解
A
B
C
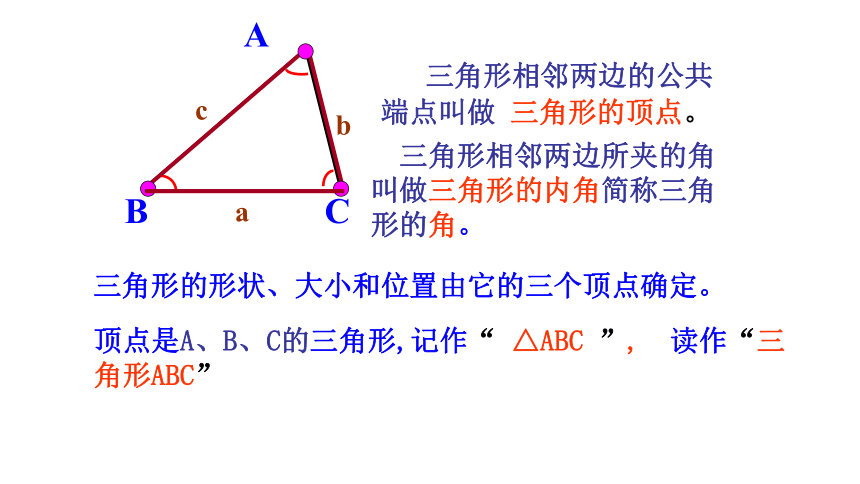
三角形相邻两边所夹的角叫做三角形的内角简称三角形的角。
a
b
c
三角形相邻两边的公共端点叫做 三角形的顶点。
顶点是A、B、C的三角形,记作“ △ABC ”, 读作“三角形ABC”
三角形的形状、大小和位置由它的三个顶点确定。
1.图中有几个三角形?用符号表示这些三角形。
2.以E为顶点的三角形有哪些?
△ ABE 、△BCE、 △ DEC
小试牛刀
3.以BC为边的三角形有哪些?
△ ABC、 △BCE、 △BCD
ΔABE、ΔABC、ΔBEC、ΔBCD、ΔECD
A
B
C
D
E
三角形的分类
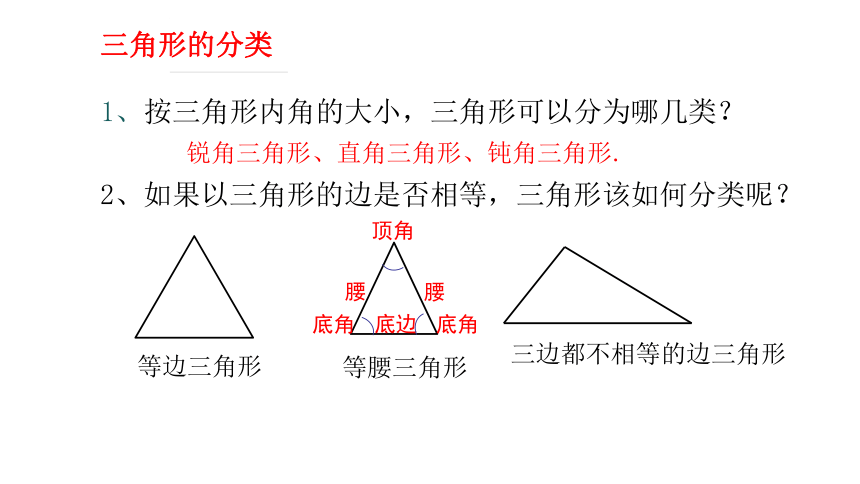
1、按三角形内角的大小,三角形可以分为哪几类?
锐角三角形、直角三角形、钝角三角形.
2、如果以三角形的边是否相等,三角形该如何分类呢?
等边三角形
三边都不相等的边三角形
等腰三角形
腰
腰
底边
顶角
底角
底角
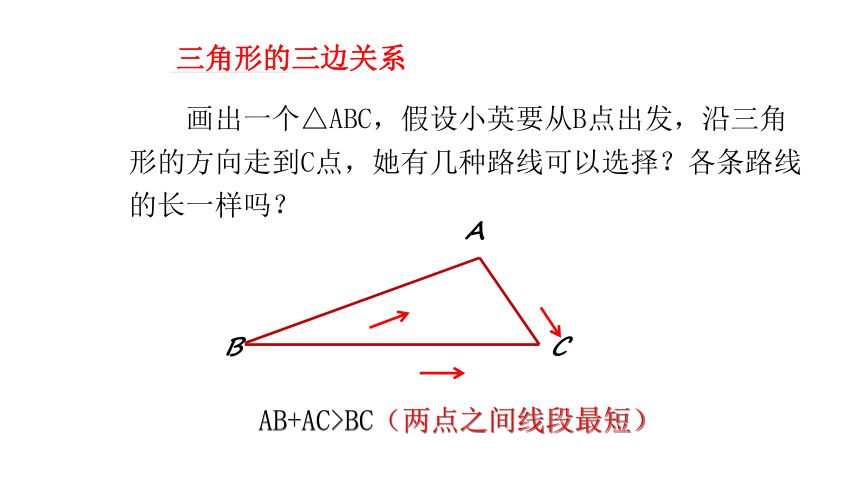
三角形的三边关系
画出一个△ABC,假设小英要从B点出发,沿三角形的方向走到C点,她有几种路线可以选择?各条路线的长一样吗?
B
C
A
AB+AC>BC(两点之间线段最短)
归纳总结
三角形两边的和大于第三边.
三角形两边的差小于第三边.
如何判断三条线段能否组成三角形
a+b>c
b+c>a
c+a>b
b
c
a
A
B
C
反之:
三角形的 任何两边之和大于
第三边
任何
判断方法:
(1)找出最长线段。
(2)比较大小:较短两边之和与最长线段的大小
(3)判断能否组成三角形。
则不能构成三角形.
只要满足较小的两条线段之和大于最长线 段,便可构成三角形;
若不满足,
长度为10cm, 5cm, 6cm三条线段能否组成三角形?
解:∵10+5>6
5+6>10
10+6>5
∴能组成三角形
解: ∵最长线段是 10cm
5+6>10
∴能组成三角形
1.三角形是指( )
A.由三条线段所组成的封闭图形
B.由不在同一直线上的三条直线首尾顺次相接组成
的图形
C.由不在同一直线上的三条线段首尾顺次相接组成
的图形
D.由三条线段首尾顺次相接组成的图形
C
2.已知等腰三角形的两边长分别为8cm,3cm,则这个三角形的周长为 ( ) A. 14cm B.19cm
C.14cm或19cm D. 不确定
B
3.如图,在△ACE中,∠ACD的对边是 .
A
B
F
E
D
C
AD
4.如图,请写出:
(1)图中各三角形;
(2)每一个三角形的三条边和三个内角。
A
D
C
B
ABC
ADC
ABC
在 中,有AB,AC,BC和∠CAB,∠B,∠BCA
ADC
在 中,有AD,AC,DC和∠DAC,∠D,∠DCA
5.如图,在△ABC中,D是AB是一点,且AD=AC,连结CD.用“>”或“<”号填入下面各个空格,并说明理由。
(1)2AD____CD;
(2) AB____AC + BC
A
B
D
C
>
<
他本想直接走路线AB,只可惜被无情的湖水挡住了去路,经过观察他除了A P B之外又发现了一 条线路A Q B,你说他该走哪条路线近一些呢
P
A
B
Q
小东学了本节课后从A处的学校回B处的家,
你能运用所学的知识说明理由吗
C
提示:延长AQ交PB于C
AP+PC>AQ+QC QC+BC>QB
所以 AP+PB>AQ+QB
1、若a,b,c是△ABC的三边长,
化简|a-b-c|+|b-c-a|+|c+a-b|.
解:根据三角形的三边关系,两边之和
大于第三边,得
a-b-c<0,b-c-a<0,c+a-b>0.
∴|a-b-c|+|b-c-a|+|c+a-b|
=-(a-b-c) -(b-c-a)+ c+a-b
=b+c-a+c+a-b+c+a-b
=3c+a-b.
A
C
B
a
c
b
三角形
定义及其基本要素
顶点、角、边
分类
按角分类
按边分类分类
不重不漏
三边关系
原理
两点之间线段最短
内容
两边之和大于第三边
两边之差小于第三边
|a-b|b,x为第三边)
应用
导入新课
定义: 由不在同一条直线上的三条线段 首尾顺次连接所组成的图形叫做三角形。
A
B
C
观察并思考:
三角形是由什么图形组成的
组成三角形的三条线段叫做三角形的边。
三角形的三边,有时也用a、b、c来表示.
a
b
c
新课讲解
A
B
C
三角形相邻两边所夹的角叫做三角形的内角简称三角形的角。
a
b
c
三角形相邻两边的公共端点叫做 三角形的顶点。
顶点是A、B、C的三角形,记作“ △ABC ”, 读作“三角形ABC”
三角形的形状、大小和位置由它的三个顶点确定。
1.图中有几个三角形?用符号表示这些三角形。
2.以E为顶点的三角形有哪些?
△ ABE 、△BCE、 △ DEC
小试牛刀
3.以BC为边的三角形有哪些?
△ ABC、 △BCE、 △BCD
ΔABE、ΔABC、ΔBEC、ΔBCD、ΔECD
A
B
C
D
E
三角形的分类
1、按三角形内角的大小,三角形可以分为哪几类?
锐角三角形、直角三角形、钝角三角形.
2、如果以三角形的边是否相等,三角形该如何分类呢?
等边三角形
三边都不相等的边三角形
等腰三角形
腰
腰
底边
顶角
底角
底角
三角形的三边关系
画出一个△ABC,假设小英要从B点出发,沿三角形的方向走到C点,她有几种路线可以选择?各条路线的长一样吗?
B
C
A
AB+AC>BC(两点之间线段最短)
归纳总结
三角形两边的和大于第三边.
三角形两边的差小于第三边.
如何判断三条线段能否组成三角形
a+b>c
b+c>a
c+a>b
b
c
a
A
B
C
反之:
三角形的 任何两边之和大于
第三边
任何
判断方法:
(1)找出最长线段。
(2)比较大小:较短两边之和与最长线段的大小
(3)判断能否组成三角形。
则不能构成三角形.
只要满足较小的两条线段之和大于最长线 段,便可构成三角形;
若不满足,
长度为10cm, 5cm, 6cm三条线段能否组成三角形?
解:∵10+5>6
5+6>10
10+6>5
∴能组成三角形
解: ∵最长线段是 10cm
5+6>10
∴能组成三角形
1.三角形是指( )
A.由三条线段所组成的封闭图形
B.由不在同一直线上的三条直线首尾顺次相接组成
的图形
C.由不在同一直线上的三条线段首尾顺次相接组成
的图形
D.由三条线段首尾顺次相接组成的图形
C
2.已知等腰三角形的两边长分别为8cm,3cm,则这个三角形的周长为 ( ) A. 14cm B.19cm
C.14cm或19cm D. 不确定
B
3.如图,在△ACE中,∠ACD的对边是 .
A
B
F
E
D
C
AD
4.如图,请写出:
(1)图中各三角形;
(2)每一个三角形的三条边和三个内角。
A
D
C
B
ABC
ADC
ABC
在 中,有AB,AC,BC和∠CAB,∠B,∠BCA
ADC
在 中,有AD,AC,DC和∠DAC,∠D,∠DCA
5.如图,在△ABC中,D是AB是一点,且AD=AC,连结CD.用“>”或“<”号填入下面各个空格,并说明理由。
(1)2AD____CD;
(2) AB____AC + BC
A
B
D
C
>
<
他本想直接走路线AB,只可惜被无情的湖水挡住了去路,经过观察他除了A P B之外又发现了一 条线路A Q B,你说他该走哪条路线近一些呢
P
A
B
Q
小东学了本节课后从A处的学校回B处的家,
你能运用所学的知识说明理由吗
C
提示:延长AQ交PB于C
AP+PC>AQ+QC QC+BC>QB
所以 AP+PB>AQ+QB
1、若a,b,c是△ABC的三边长,
化简|a-b-c|+|b-c-a|+|c+a-b|.
解:根据三角形的三边关系,两边之和
大于第三边,得
a-b-c<0,b-c-a<0,c+a-b>0.
∴|a-b-c|+|b-c-a|+|c+a-b|
=-(a-b-c) -(b-c-a)+ c+a-b
=b+c-a+c+a-b+c+a-b
=3c+a-b.
A
C
B
a
c
b
三角形
定义及其基本要素
顶点、角、边
分类
按角分类
按边分类分类
不重不漏
三边关系
原理
两点之间线段最短
内容
两边之和大于第三边
两边之差小于第三边
|a-b|
应用
