11.1.1 三角形的边 课件(共29张PPT)
文档属性
| 名称 | 11.1.1 三角形的边 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-24 08:56:15 | ||
图片预览



文档简介
(共29张PPT)
11.1.1 三角形的边
人教版八年级上册
教学目标
1.知道三角形的顶点、边、角的表示方法.
2.掌握三角形的三边关系,能利用该关系判断三条线段能否组成三角形.
新知导入
三角形是一种基本的几何图形.从古至今,三角形被非常广泛的运用在生产、生活中,小到螺丝、饰品,大到高楼大厦,那为什么生产、生活中,经常采用三角形的结构呢
新知探究
三角形的有关概念
知识点 1
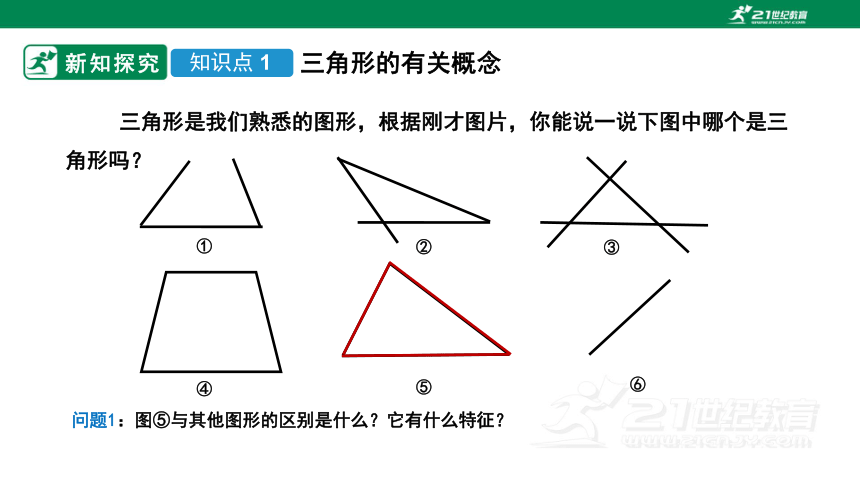
三角形是我们熟悉的图形,根据刚才图片,你能说一说下图中哪个是三角形吗?
①
②
③
④
⑤
⑥
问题1:图⑤与其他图形的区别是什么?它有什么特征?
新知探究
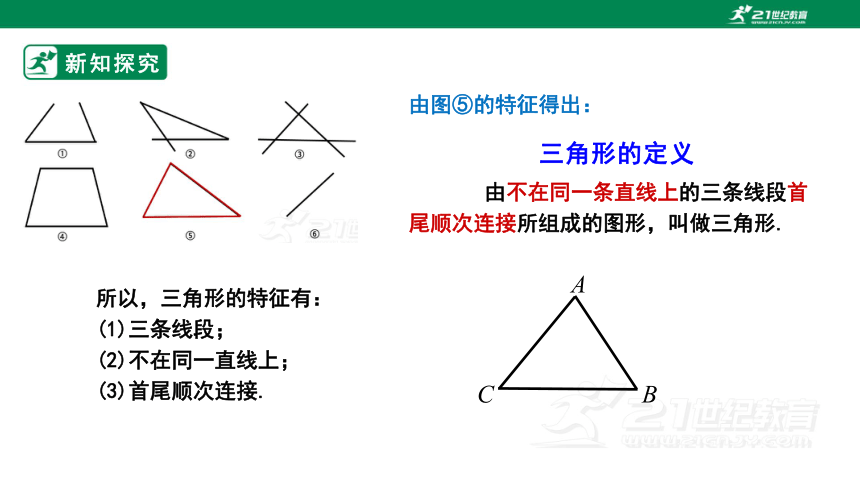
由不在同一条直线上的三条线段首尾顺次连接所组成的图形,叫做三角形.
三角形的定义
所以,三角形的特征有:
(1)三条线段;
(2)不在同一直线上;
(3)首尾顺次连接.
由图⑤的特征得出:
A
B
C
新知探究
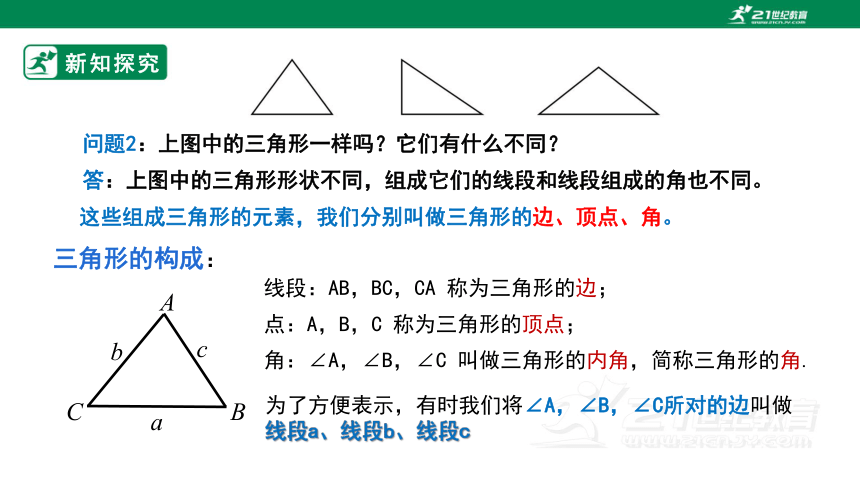
问题2:上图中的三角形一样吗?它们有什么不同?
答:上图中的三角形形状不同,组成它们的线段和线段组成的角也不同。
这些组成三角形的元素,我们分别叫做三角形的边、顶点、角。
三角形的构成:
A
B
C
b
a
c
线段:AB,BC,CA 称为三角形的边;
点:A,B,C 称为三角形的顶点;
角:∠A,∠B,∠C 叫做三角形的内角,简称三角形的角.
为了方便表示,有时我们将∠A,∠B,∠C所对的边叫做线段a、线段b、线段c
新知探究
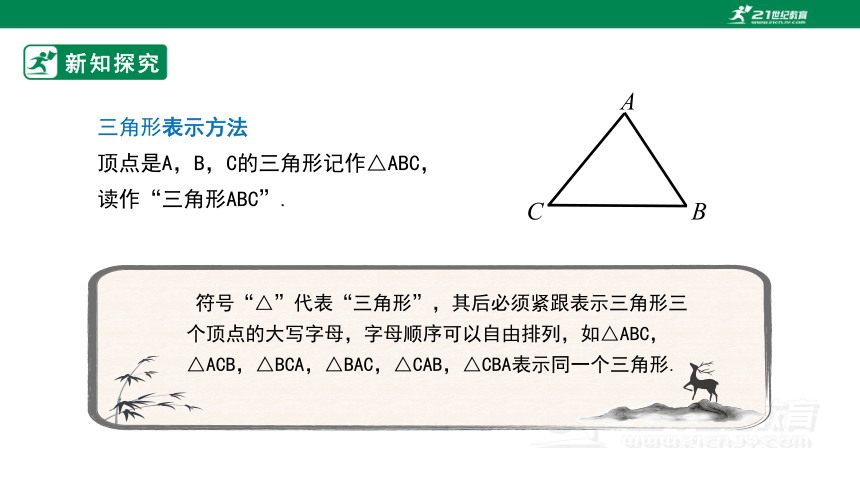
三角形表示方法
顶点是A,B,C的三角形记作△ABC,
读作“三角形ABC”.
A
B
C
符号“△”代表“三角形”,其后必须紧跟表示三角形三个顶点的大写字母,字母顺序可以自由排列,如△ABC,△ACB,△BCA,△BAC,△CAB,△CBA表示同一个三角形.
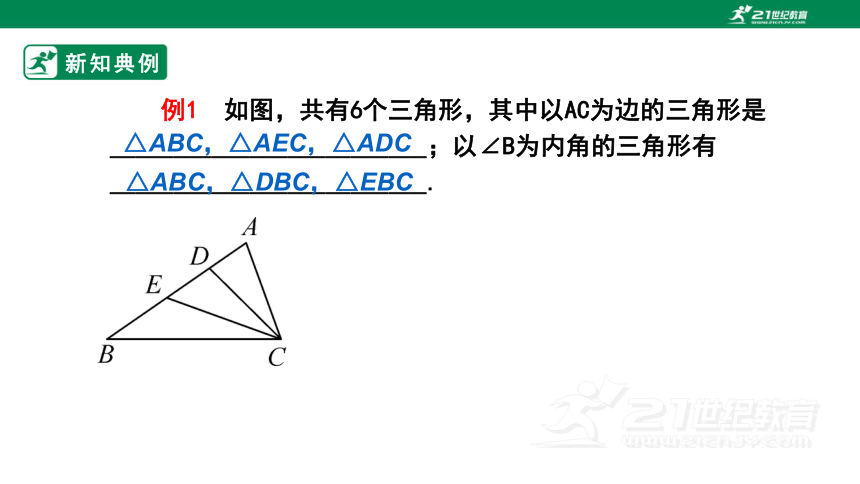
例1 如图,共有6个三角形,其中以AC为边的三角形是_________________________;以∠B为内角的三角形有_________________________.
新知典例
△ABC,△AEC,△ADC
△ABC,△DBC,△EBC
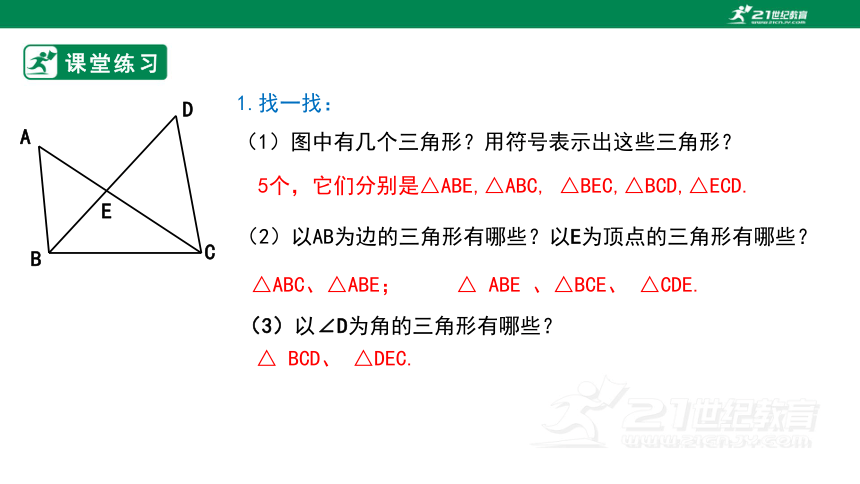
课堂练习
1.找一找:
(1)图中有几个三角形?用符号表示出这些三角形?
A
B
C
D
E
5个,它们分别是△ABE,△ABC, △BEC,△BCD,△ECD.
(2)以AB为边的三角形有哪些?以E为顶点的三角形有哪些?
△ABC、△ABE;
△ ABE 、△BCE、 △CDE.
(3)以∠D为角的三角形有哪些?
△ BCD、 △DEC.
新知探究
三角形的分类
知识点 2
问题1:按照三角形内角的大小,三角形可以分为哪几类?
锐角三角形
直角三角形
钝角三角形
三角形
新知探究
A
B
C
三边都相等的三角形
等边三角形
有两条边相等的三角形
等腰三角形
A
B
C
三条边都不相等的三角形
腰
腰
底边
顶角
底角
底角
问题2:按照三角形边的相等关系,三角形可以分为哪几类?
新知探究
三边都不相等的三角形
等腰三角形
三角形
底边和腰不相等的等腰三角形
等边三角形
三角形按边的相等关系分类
新知典例
例2 下列说法正确的有( ).
①等腰三角形是等边三角形;
②三角形按边可分为等腰三角形、等边三角形和不等
边三角形;
③等腰三角形至少有两边相等;
④三角形按角可分为锐角三角形、直角三角形和钝角
三角形.
A.①② B.①③④ C.③④ D.①②④
C
课堂练习
2.根据下列条件,判断△ABC的形状.
①∠A=45°,∠B=65°,∠C=70°;
②∠C=110°; ③∠C=90°; ④AB=BC=3,AC=4
解:①∵∠A,∠B,∠C都小于90°,
∴△ABC是锐角三角形
②∵∠C=110°>90°,∴△ABC是钝角三角形
③∵∠C=90°=90°, ∴△ABC是直角三角形
④∵AB=BC=3,AC=4,∴△ABC是等腰三角形
新知探究
知识点 3
三角形三边的关系
在A点的小狗,为了尽快吃到B点的香肠,它会选择哪条路线 如果小狗在C点呢?
B
C
A
C
A
B
路线1:从点A直接到点B
长度:AB
路线2:从点A到点C,再从点C到点B,
长度:AC+CB.
新知探究
思考:在一个三角形中,任意两边之和与第三边的长度有怎样的关系呢?
A
C
B
小结:三角形两边的和大于第三边.
A
C
B
A
C
B
BA+AC>BC
AC+BC>AB
CB+BA>AC
新知探究
BA > BC-AC
AC+CB > AB
BA+AC > BC
CB+BA > CA
AC > AB-CB
CB > CA-BA
A
C
B
思考:在一个三角形中,任意两边之差与第三边的长度有怎样的关系呢?
移项
小结:三角形两边的差小于第三边.
课堂总结
A
C
B
三角形的三边关系:
1、三角形两边的和大于第三边;
2、三角形两边的差小于第三边.
注意:判断三条线段能否组成三角形,只需判断“两条较短的线段之和大于第三条”即可.
新知典例
例3 下列长度的各组线段能否组成一个三角形?
(1)15cm、10cm、6cm (2) 4cm、5cm、10cm
(3) 4cm、9cm、5cm (4) 3cm、4cm、5cm
(2) 因为4cm+5cm<10cm,所以这三条线段不能组成一个三角形.
(3) 因为4cm+5cm=9cm, 所以这三条线段不能组成一个三角形.
(1) 因为10cm+6cm>15cm, 所以这三条线段能组成一个三角形.
解:
(4) 因为3cm+4cm>5cm,所以这三条线段能组成一个三角形.
新知典例
例4.小王准备用一段长30m的篱笆围成一个三角形状的场地,用于饲养家兔,已知第一条边长为am,由于受地势限制,第二条边长只能是第一条边长的2倍多2m.
(1)请用a表示第三条边长.
(2)问第一条边长可以为7m吗?请说明理由.
解:(1)第三边为:30﹣a﹣(2a+2)=(28﹣3a)m.
(2)第一条边长不可以为7m.
理由:a=7时,三边分别为7,16,7,
∵7+7<16,
∴不能构成三角形,即第一条边长不可以为7m.
课堂练习
1.下列长度的三条线段中,能组成三角形的是( )
A.1cm,2cm,3cm B.2cm,3cm,4cm
C.4cm,6cm,10cm D.5cm,8cm,14cm
B
2.某三角形的三边长分别为3,6,x,则x可能是( )
A.3 B.9 C.6 D.10
C
课堂小测
1.有下列两种图示均表示三角形分类,则正确的是( )
A.①对,②不对 B.②对,①不对
C.①、②都不对 D.①、②都对
B
课堂小测
2.如图所示,以BC为边的三角形共有( )
A.1个 B.2个 C.3个 D.4个
C
课堂小测
3.若长度分别是3,a﹣2,5的三条线段能组成一个三角形,则a的值不可能是( )
A.4 B.6 C.8 D.9
A
4.已知一个三角形的两边长分别是2cm和4cm,第三边长x是奇数,则x的值是 .
3cm或5cm
课堂小测
5.已知三角形的三边长为4、x、10,化简:|x﹣5|+|x﹣15|= .
10
6.a,b,c是三角形的三边长,化简|a﹣b﹣c|﹣|b﹣c+a|+|c﹣a﹣b|=
.
b+c﹣a
课堂小测
7.若一个三角形的三边长分别是a,b,c,其中a和b满足方程
,若这个三角形的周长为整数,求这个三角形的周长.
解:解方程组
,得
则4﹣1<c<4+1,即3<c<5,
∵周长为整数,
∴c=4,
∴三角形的周长=4+4+1=9.
课堂总结
概念
三角形
三角形的分类
三角形的三边关系
按角分类
按边分类
三角形两边的和
大于第三边
三角形两边的差
小于第三边
边、顶点、角
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
11.1.1 三角形的边
人教版八年级上册
教学目标
1.知道三角形的顶点、边、角的表示方法.
2.掌握三角形的三边关系,能利用该关系判断三条线段能否组成三角形.
新知导入
三角形是一种基本的几何图形.从古至今,三角形被非常广泛的运用在生产、生活中,小到螺丝、饰品,大到高楼大厦,那为什么生产、生活中,经常采用三角形的结构呢
新知探究
三角形的有关概念
知识点 1
三角形是我们熟悉的图形,根据刚才图片,你能说一说下图中哪个是三角形吗?
①
②
③
④
⑤
⑥
问题1:图⑤与其他图形的区别是什么?它有什么特征?
新知探究
由不在同一条直线上的三条线段首尾顺次连接所组成的图形,叫做三角形.
三角形的定义
所以,三角形的特征有:
(1)三条线段;
(2)不在同一直线上;
(3)首尾顺次连接.
由图⑤的特征得出:
A
B
C
新知探究
问题2:上图中的三角形一样吗?它们有什么不同?
答:上图中的三角形形状不同,组成它们的线段和线段组成的角也不同。
这些组成三角形的元素,我们分别叫做三角形的边、顶点、角。
三角形的构成:
A
B
C
b
a
c
线段:AB,BC,CA 称为三角形的边;
点:A,B,C 称为三角形的顶点;
角:∠A,∠B,∠C 叫做三角形的内角,简称三角形的角.
为了方便表示,有时我们将∠A,∠B,∠C所对的边叫做线段a、线段b、线段c
新知探究
三角形表示方法
顶点是A,B,C的三角形记作△ABC,
读作“三角形ABC”.
A
B
C
符号“△”代表“三角形”,其后必须紧跟表示三角形三个顶点的大写字母,字母顺序可以自由排列,如△ABC,△ACB,△BCA,△BAC,△CAB,△CBA表示同一个三角形.
例1 如图,共有6个三角形,其中以AC为边的三角形是_________________________;以∠B为内角的三角形有_________________________.
新知典例
△ABC,△AEC,△ADC
△ABC,△DBC,△EBC
课堂练习
1.找一找:
(1)图中有几个三角形?用符号表示出这些三角形?
A
B
C
D
E
5个,它们分别是△ABE,△ABC, △BEC,△BCD,△ECD.
(2)以AB为边的三角形有哪些?以E为顶点的三角形有哪些?
△ABC、△ABE;
△ ABE 、△BCE、 △CDE.
(3)以∠D为角的三角形有哪些?
△ BCD、 △DEC.
新知探究
三角形的分类
知识点 2
问题1:按照三角形内角的大小,三角形可以分为哪几类?
锐角三角形
直角三角形
钝角三角形
三角形
新知探究
A
B
C
三边都相等的三角形
等边三角形
有两条边相等的三角形
等腰三角形
A
B
C
三条边都不相等的三角形
腰
腰
底边
顶角
底角
底角
问题2:按照三角形边的相等关系,三角形可以分为哪几类?
新知探究
三边都不相等的三角形
等腰三角形
三角形
底边和腰不相等的等腰三角形
等边三角形
三角形按边的相等关系分类
新知典例
例2 下列说法正确的有( ).
①等腰三角形是等边三角形;
②三角形按边可分为等腰三角形、等边三角形和不等
边三角形;
③等腰三角形至少有两边相等;
④三角形按角可分为锐角三角形、直角三角形和钝角
三角形.
A.①② B.①③④ C.③④ D.①②④
C
课堂练习
2.根据下列条件,判断△ABC的形状.
①∠A=45°,∠B=65°,∠C=70°;
②∠C=110°; ③∠C=90°; ④AB=BC=3,AC=4
解:①∵∠A,∠B,∠C都小于90°,
∴△ABC是锐角三角形
②∵∠C=110°>90°,∴△ABC是钝角三角形
③∵∠C=90°=90°, ∴△ABC是直角三角形
④∵AB=BC=3,AC=4,∴△ABC是等腰三角形
新知探究
知识点 3
三角形三边的关系
在A点的小狗,为了尽快吃到B点的香肠,它会选择哪条路线 如果小狗在C点呢?
B
C
A
C
A
B
路线1:从点A直接到点B
长度:AB
路线2:从点A到点C,再从点C到点B,
长度:AC+CB.
新知探究
思考:在一个三角形中,任意两边之和与第三边的长度有怎样的关系呢?
A
C
B
小结:三角形两边的和大于第三边.
A
C
B
A
C
B
BA+AC>BC
AC+BC>AB
CB+BA>AC
新知探究
BA > BC-AC
AC+CB > AB
BA+AC > BC
CB+BA > CA
AC > AB-CB
CB > CA-BA
A
C
B
思考:在一个三角形中,任意两边之差与第三边的长度有怎样的关系呢?
移项
小结:三角形两边的差小于第三边.
课堂总结
A
C
B
三角形的三边关系:
1、三角形两边的和大于第三边;
2、三角形两边的差小于第三边.
注意:判断三条线段能否组成三角形,只需判断“两条较短的线段之和大于第三条”即可.
新知典例
例3 下列长度的各组线段能否组成一个三角形?
(1)15cm、10cm、6cm (2) 4cm、5cm、10cm
(3) 4cm、9cm、5cm (4) 3cm、4cm、5cm
(2) 因为4cm+5cm<10cm,所以这三条线段不能组成一个三角形.
(3) 因为4cm+5cm=9cm, 所以这三条线段不能组成一个三角形.
(1) 因为10cm+6cm>15cm, 所以这三条线段能组成一个三角形.
解:
(4) 因为3cm+4cm>5cm,所以这三条线段能组成一个三角形.
新知典例
例4.小王准备用一段长30m的篱笆围成一个三角形状的场地,用于饲养家兔,已知第一条边长为am,由于受地势限制,第二条边长只能是第一条边长的2倍多2m.
(1)请用a表示第三条边长.
(2)问第一条边长可以为7m吗?请说明理由.
解:(1)第三边为:30﹣a﹣(2a+2)=(28﹣3a)m.
(2)第一条边长不可以为7m.
理由:a=7时,三边分别为7,16,7,
∵7+7<16,
∴不能构成三角形,即第一条边长不可以为7m.
课堂练习
1.下列长度的三条线段中,能组成三角形的是( )
A.1cm,2cm,3cm B.2cm,3cm,4cm
C.4cm,6cm,10cm D.5cm,8cm,14cm
B
2.某三角形的三边长分别为3,6,x,则x可能是( )
A.3 B.9 C.6 D.10
C
课堂小测
1.有下列两种图示均表示三角形分类,则正确的是( )
A.①对,②不对 B.②对,①不对
C.①、②都不对 D.①、②都对
B
课堂小测
2.如图所示,以BC为边的三角形共有( )
A.1个 B.2个 C.3个 D.4个
C
课堂小测
3.若长度分别是3,a﹣2,5的三条线段能组成一个三角形,则a的值不可能是( )
A.4 B.6 C.8 D.9
A
4.已知一个三角形的两边长分别是2cm和4cm,第三边长x是奇数,则x的值是 .
3cm或5cm
课堂小测
5.已知三角形的三边长为4、x、10,化简:|x﹣5|+|x﹣15|= .
10
6.a,b,c是三角形的三边长,化简|a﹣b﹣c|﹣|b﹣c+a|+|c﹣a﹣b|=
.
b+c﹣a
课堂小测
7.若一个三角形的三边长分别是a,b,c,其中a和b满足方程
,若这个三角形的周长为整数,求这个三角形的周长.
解:解方程组
,得
则4﹣1<c<4+1,即3<c<5,
∵周长为整数,
∴c=4,
∴三角形的周长=4+4+1=9.
课堂总结
概念
三角形
三角形的分类
三角形的三边关系
按角分类
按边分类
三角形两边的和
大于第三边
三角形两边的差
小于第三边
边、顶点、角
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
