苏教版数学六年级上册单元测试卷-第一单元 长方体和正方体(含答案)
文档属性
| 名称 | 苏教版数学六年级上册单元测试卷-第一单元 长方体和正方体(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 188.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-23 11:01:52 | ||
图片预览



文档简介
苏教版数学六年级上册单元测试卷
第一单元 长方体和正方体
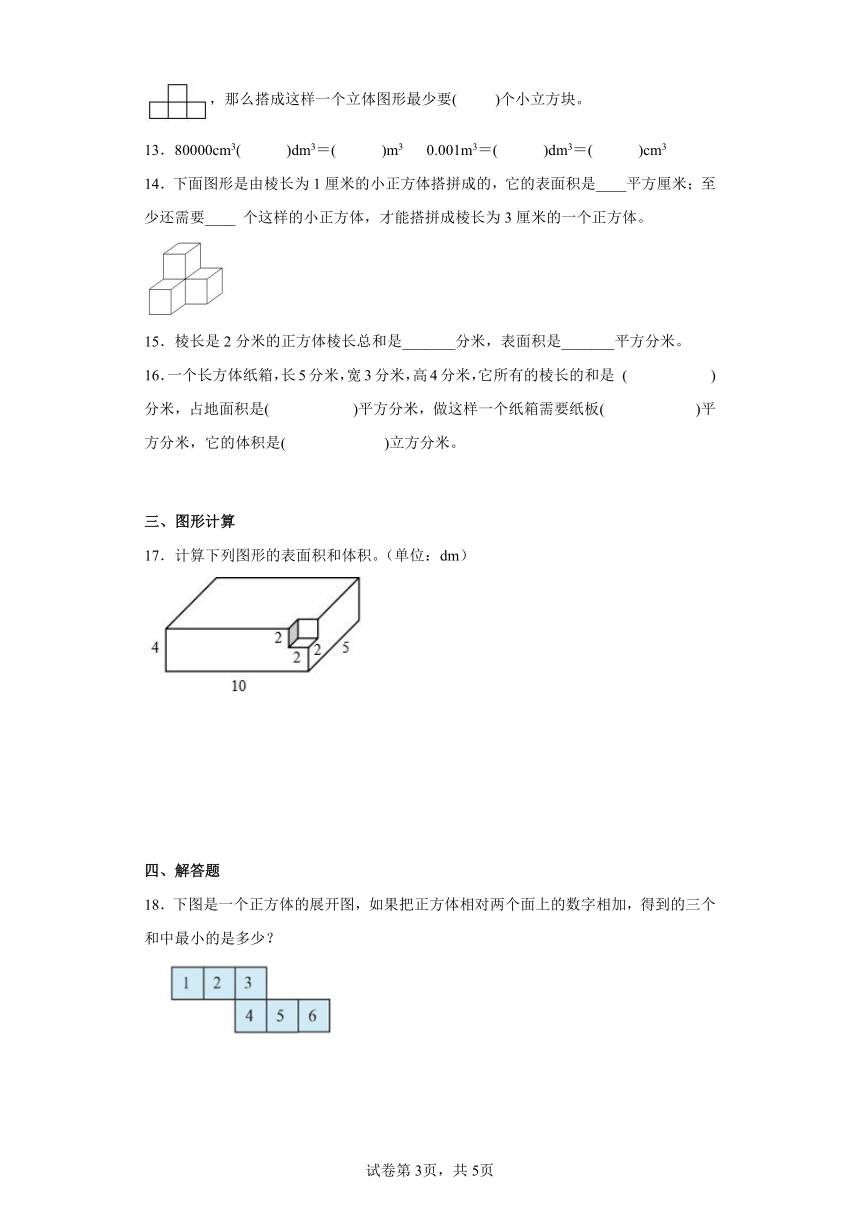
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.如图,有一个无盖的正方体纸盒,下底标有字母“M”,如果沿图中粗线将其剪开并展开成平面图形想想会是( )。
B.
C. D.
2.用8个小正方体拼成一个大正方体,如右图,现在把画“×”的两个正方体拿走,它的表面积和原来比( )。
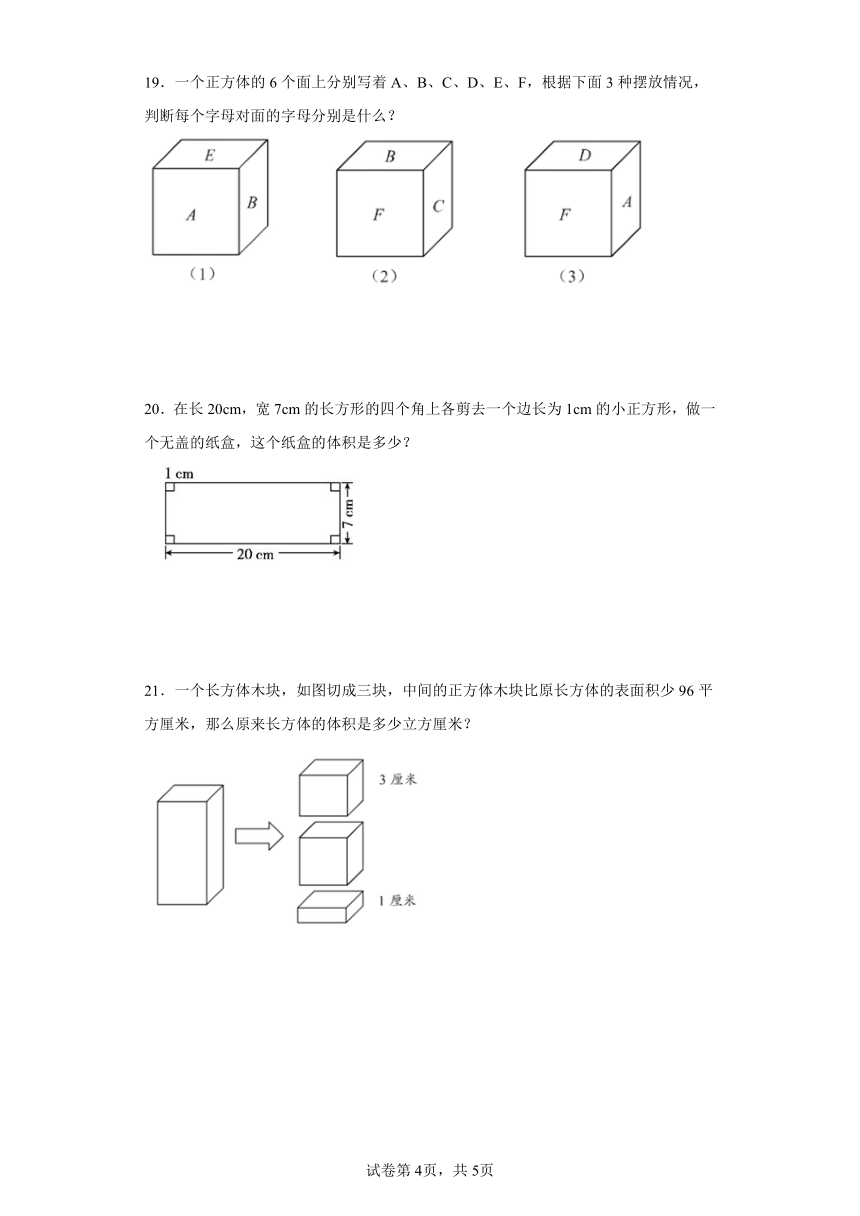
A.不变 B.增加了 C.减少了
3.小丽制作了一个如图所示的正方体礼品盒,其对面图案都相同,那么这个正方体的平面展开图可能是( )
B.
C. D.
4.下图是一个棱长4厘米的正方体,在正方体上面正中向下挖一个棱长是2厘米的正方体小洞,接着在小洞的底面正中再向下挖一个棱长是1厘米正方体小洞,最后得到的立方体图形的表面积是( )平方厘米。
A.96 B.116 C.128 D.132
5.用12个小正方体可以拼成( )种不同的长方体.
A.3 B.4 C.5 D.6
6.一个正方体的木料,它的底面积是10平方厘米,把它横截成4段,表面积增加( ) 平方厘米。
A.20 B.40 C.60
7.把一个棱长为4dm的正方体切成两个相同的长方体,每个长方体的表面积是( )。
A.48dm2 B.64dm2 C.40dm2 D.60dm2
8.有三个相同的骰子摆放如下图,底面点数之和最小是( )。
A.10 B.11 C.12 D.无法判断
二、填空题
9.用一根520厘米长的木条,恰好可以做一个长60厘米、宽40厘米、高( )分米的长方体木框。
10.长7分米,宽4分米,高6分米的长方体盒子,最多能放( )个棱长是2分米的正方体的木块。
11.把两个棱长为2厘米的正方体拼成一个长方体,这个长方体的表面积是( )平方厘米。
12.一个用立方块搭成的立体图形,小明从前面看到的图形是,从上面看是,那么搭成这样一个立体图形最少要( )个小立方块。
13.80000cm3( )dm3=( )m3 0.001m3=( )dm3=( )cm3
14.下面图形是由棱长为1厘米的小正方体搭拼成的,它的表面积是____平方厘米;至少还需要____ 个这样的小正方体,才能搭拼成棱长为3厘米的一个正方体。
15.棱长是2分米的正方体棱长总和是_______分米,表面积是_______平方分米。
16.一个长方体纸箱,长5分米,宽3分米,高4分米,它所有的棱长的和是 ( )分米,占地面积是( )平方分米,做这样一个纸箱需要纸板( )平方分米,它的体积是( )立方分米。
三、图形计算
17.计算下列图形的表面积和体积。(单位:dm)
四、解答题
18.下图是一个正方体的展开图,如果把正方体相对两个面上的数字相加,得到的三个和中最小的是多少?
19.一个正方体的6个面上分别写着A、B、C、D、E、F,根据下面3种摆放情况,判断每个字母对面的字母分别是什么?
20.在长20cm,宽7cm的长方形的四个角上各剪去一个边长为1cm的小正方形,做一个无盖的纸盒,这个纸盒的体积是多少?
21.一个长方体木块,如图切成三块,中间的正方体木块比原长方体的表面积少96平方厘米,那么原来长方体的体积是多少立方厘米?
22.用彩带捆扎下面的礼品盒,需要多少厘米彩带?(彩带结长15厘米)
23.一个无盖玻璃鱼缸的形状是正方体,棱长是3分米,制作这个鱼缸至少需要多大面积的玻璃?这个鱼缸可以容水多少升?
24.一根铁丝长120cm,现将这根铁丝焊接成一个正方体的模型.这个正方体的体积是多少立方厘米?
25.把一个铁块放入一个长为40厘米,宽为15厘米的长方体水槽中,水面上升了3厘米,这个铁块的体积是多少立方厘米?
26.把三个完全相同的正方体摆成一个长方体,这个长方体的表面积是224平方厘米,每个正方体的表面积是多少平方厘米?
27.把一张长20厘米、宽12厘米的硬纸板,从四个角各剪去一个正方形,再折成一个高2厘米的长方体无盖纸盒。这个纸盒的容积是多少平方厘米?
试卷第1页,共3页
试卷第2页,共2页
参考答案:
1.B
【分析】一个无盖的正方体纸盒,下底标有字母“M”,沿图中粗线将其展开成平面图形,则是正方体展开图的“1-4-1”形中的“1-4”,且是右端对齐。据此可以解答。
【详解】有一个无盖的正方体纸盒,下底标有字母“M”,沿图中粗线将其展开成平面图形是:
故答案为:B
【点睛】此题考查正方体的表面展开图,需熟练掌握正方体表面展开图的特征。
2.C
【详解】【错误答案】A
【错因】 错以为此题中顶点处正方体拿走不影响表面积。
【改正】 C
【反思】正方体顶点处拿走一个正方体,不影响表面积,拿走多个应具体分析,此题减少左右两个面的面积。
3.A
【分析】如图,这个正方体礼品盒中,其对面图案都相同,图A折叠成正方体礼盒后,心与心相对,笑脸与笑脸相对,太阳与太阳相对;图B折叠成正方体礼盒后,心与太阳相对,笑脸与笑脸相对;图C折叠成正方体礼盒后,心与心相对,笑脸与太阳相对;图D折叠成正方体礼盒后,心与笑脸相对,太阳与太阳相对.
【详解】根据分析,图A折叠成正方体礼盒后,心与心相对,笑脸与笑脸相对,太阳与太阳相对,即对面图案相同;
图B、图C和图D中对面图案不相同;
故选A.
4.B
【分析】观察图可知:最后得到的立方体图形的表面积=大正方体的表面积+两个小正方体4个侧面面积的和,将数值代入正方体表面积公式中计算即可。
【详解】最后得到的立方体图形的表面积:
42×6+22×4+12×4
=96+16+4
=116(平方厘米)
故答案为:B
【点睛】本题考查正方体表面积公式的应用,关键要理解求得是哪几个面的面积和。
5.B
【解析】略
6.C
【分析】由题意知:正方体的木料,它的底面积是10平方厘米,它的其余的面的面积也是10平方厘米。横截成4段后,增加了6个面。据此解答。
【详解】6×10=60(平方厘米)
故答案为:C
【点睛】理解横截成4段,增加6个面的表面积是解答本题的关键。
7.B
【解析】略
8.B
【详解】略
9.3
【分析】根据长方体的棱长公式:(长+宽+高)×4,已知长方体的长、宽和总棱长求高,代入公式,即可解答。
【详解】520÷4-60-40
=130-60-40
=70-40
=30(厘米)
30厘米=3分米
【点睛】本题考查长方体的特点,根据长方体的特点进行解答,注意单位换算。
10.18
【详解】以长为边最多放7÷2=3(块)……1(分米)
以宽为边最多放4÷2=2(块)
以高为边最多放6÷2=3(块)
所以:3×2×3=18(块)
【点睛】长方体里放木块应根据实际情况,先求出每条棱长上最多能放的块数,再借助长方体的体积公式进行计算。
11.40
【分析】把两个棱长为2厘米的正方体拼成一个长方体,长方体的表面积比原来2个正方体的面积减少2个面的面积,据此解答。
【详解】2×2×(6×2-2)
=4×10
=40(平方厘米)
【点睛】考查了立体图形的切拼,此题也可以通过分析出长方体的长、宽、高,根据长方体的面积公式解答。
12.5
【分析】从前面看该立体图形有两层,下层3个,上层中间1个;上面看该立体图形有两行,上行中间1个,下行3个;所以搭成这样一个立体图形最少要5个小立方块。据此解答。
【详解】由分析可得:搭成这样一个立体图形最少要5个小立方块。
【点睛】根据视图求立体图形最多最少问题,从上面看的图形入手,分别标出每个位置的正方体个数。
13. 80 0.08 1 1000
【分析】将立方厘米换算成立方分米,除以进率1000,换算成立方米,除以进率1000000;
将立方米换算成立方分米,乘进率1000,换算成立方厘米,乘进率1000000。
【详解】80000cm3=80dm3=0.08 m3
0.001m3=1dm3=1000 cm3
【点睛】本题考查单位换算,牢记大单位换算小单位乘进率,小单位换算大单位除以进率。
14. 18 23
【分析】观察图形可知:从上面和下面看:分别有3个小正方体的面;从左面和右面看:分别有3个小正方体的面;从前面和后面看分别有3个小正方体的面,1个小正方体的面的面积是1×1=1平方厘米,由此即可求出这个图形的表面积;
拼组后的大正方体的每条棱长是由3个小正方体组成的,由此可以求出拼组后的大正方体中的小正方体的个数,再减去图中已有的小正方体个数即可。
【详解】3×6=18(平方厘米)
3×3×3-4
=27-4
=23(个)
【点睛】考查了立体图形的切拼,也考查了学生通过观察立体图形解决问题的能力。
15. 24 24
【分析】正方体棱长总和=棱长×12;正方体表面积=棱长×棱长×6;由此列式解答。
【详解】棱长总和:2×12=24(分米)
表面积:2×2×6
=4×6
=24(平方分米)
【点睛】题主要考查正方体的特征以及棱长总和与表面积的计算方法,直接利用公式解答即可。
16. 48 15 94 60
【分析】棱长之和=(长+宽+高)×4;占地面积=长×宽;长方体的表面积=(长×宽+长×高+宽×高)×2;长方体的体积=长×宽×高,代入数据计算即可。
【详解】(5+3+4)×4
=12×4
=48(分米)
它所有的棱长的和是48分米;
5×3=15(平方分米)
占地面积是15平方分米;
(5×3+5×4+3×4)×2
=(15+20+12)×2
=47×2
=94(平方分米)
做这样一个纸箱需要纸板94平方分米;
5×3×4=60(立方分米)
它的体积是60立方分米。
【点睛】此题考查了长方体的综合应用,掌握其棱长总和、体积和表面积的计算公式,认真计算即可。
17.220dm2;192dm3
【分析】对题中立体图形进行平移填补可知:该立体图形的表面积即是长10dm,宽5dm,高4分米的长方体的表面积,根据长方体表面积=(长×宽+长×高+宽×高)×2,代入数值计算;该立体图形的体积=大长方体体积-小立方体的体积,代入数值计算即可。
【详解】表面积:
(10×5+10×4+5×4)×2
=110×2
=220(dm2)
体积:
10×5×4-2×2×2
=200-8
=192(dm3)
18.4
【分析】符合正方体展开图的“3-3”型,折叠后,1对3;2对5;4对6;再把对应的两个数相加,即可判断最小的几,据此解答。
【详解】根据正方体展开图可知,1对3;2对5;4对6
1+3=4
2+5=7
4+6=10
4<7<10
最小的和是4
答:得到的三个和中最小的是4。
【点睛】本题考查正方体表面展开图,根据折叠后面的对应的数字,进行解答。
19.A对面为C;B对面为D;E对面为F
【分析】结合3种摆放情况,用排除法找对立面,据此解答。
【详解】由(1)(3)得A对面不可能是B、E、D、F,所以A对面为C。
由(1)(2)得B对面不可能是A、E、C、F,所以B对面为D。
则E对面为F。
【点睛】考查了立体图形找对立面的方法,学生应掌握。
20.90 cm3
【详解】7-1×2=5(cm)
20-1×2=18(cm)
18×5×1=90(cm3)
答:这个纸盒的体积是90 cm3。
21.360立方厘米
【分析】根据题意可知,减少的面积,就是上面长方体4个侧面面积和下面长方体4个侧面积面积,根据中间是正方体,上面的长方体的长和宽和下面的长方体的长和宽都等于正方体的棱长,用96除以4,就是高为3厘米和高为1厘米的长方体侧面的和,长和宽相等,进而求出这个长方体的长和宽,高等于3厘米+长方体的长+1厘米,根据长方体的体积公式:长×宽×高,即可解答。
【详解】96÷4=24(平方厘米)
长:24÷(3+1)
=24÷4
=6(厘米)
长方体的长是6厘米,宽是6厘米,高是3+6+1=10厘米
体积:6×6×10
=36×10
=360(立方厘米)
答:原来这个长方体的体积是360立方厘米。
【点睛】本题考查长方体体积公式的应用,关键是减少的面积是上面长方体4个侧面积和下面长方体4个侧面之和。
22.147厘米
【分析】仔细观察发现,六个面上与长相等的彩带有2段,长度为12厘米的彩带有6段,据此算出各段的长度再加上打结处的长度即可。
【详解】30×2+12×6
=60+72
=132(厘米)
132+15=147(厘米)
答:需要147厘米彩带。
【点睛】分别找出与长、宽、高相等的彩带段数。
23.45平方分米;27升
【分析】由于鱼缸无盖,所以只求它的5个面的总面积,根据正方形的面积公式:S=a2,求出一个面的面积再乘5即可求出制作这个鱼缸至少需要玻璃的面积;根据正方体的体积=棱长×棱长×棱长求出这个鱼缸以容水的升数。
【详解】3×3×5
=9×5
=45(平方分米)
答:制作这个鱼缸至少需要45平方分米的玻璃。
3×3×3
=9×3
=27(立方分米)
27立方分米=27升
答:这个鱼缸可以容水27升。
【点睛】考查了正方体表面积和体积的灵活应用,学生应掌握。
24.1000立方厘米
【详解】略
25.1800立方厘米
【分析】水面上生的体积就是铁块体积,用长×宽×水面上升的高度即可。
【详解】40×15×3=1800(立方厘米)
答:这个铁块的体积是1800立方厘米。
【点睛】关键是利用转化思想,将求不规则物体的体积转化为求长方体等规则物体的体积。
26.96平方厘米
【分析】3个正方体共有6×3=18个面,摆成一个长方体现在少了4个面,所以长方体是18-4=14个正方形的面,则一个面的面积是224÷14=16平方厘米,再乘6即可。如下图所示:
【详解】6×3=18(个)
18-4=14(个)
224÷14=16(平方厘米)
16×6=96(平方厘米)
答:每个正方体的表面积是96平方厘米。
【点睛】理清摆成一个长方体后有14个正方形的面是解题的关键。
27.256立方厘米
【详解】20-2×2=16(厘米)
12-2×2=8(厘米)
16×8×2=256(立方厘米)
答:这个纸盒的容积是256平方厘米。
答案第1页,共2页
答案第1页,共2页
第一单元 长方体和正方体
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.如图,有一个无盖的正方体纸盒,下底标有字母“M”,如果沿图中粗线将其剪开并展开成平面图形想想会是( )。
B.
C. D.
2.用8个小正方体拼成一个大正方体,如右图,现在把画“×”的两个正方体拿走,它的表面积和原来比( )。
A.不变 B.增加了 C.减少了
3.小丽制作了一个如图所示的正方体礼品盒,其对面图案都相同,那么这个正方体的平面展开图可能是( )
B.
C. D.
4.下图是一个棱长4厘米的正方体,在正方体上面正中向下挖一个棱长是2厘米的正方体小洞,接着在小洞的底面正中再向下挖一个棱长是1厘米正方体小洞,最后得到的立方体图形的表面积是( )平方厘米。
A.96 B.116 C.128 D.132
5.用12个小正方体可以拼成( )种不同的长方体.
A.3 B.4 C.5 D.6
6.一个正方体的木料,它的底面积是10平方厘米,把它横截成4段,表面积增加( ) 平方厘米。
A.20 B.40 C.60
7.把一个棱长为4dm的正方体切成两个相同的长方体,每个长方体的表面积是( )。
A.48dm2 B.64dm2 C.40dm2 D.60dm2
8.有三个相同的骰子摆放如下图,底面点数之和最小是( )。
A.10 B.11 C.12 D.无法判断
二、填空题
9.用一根520厘米长的木条,恰好可以做一个长60厘米、宽40厘米、高( )分米的长方体木框。
10.长7分米,宽4分米,高6分米的长方体盒子,最多能放( )个棱长是2分米的正方体的木块。
11.把两个棱长为2厘米的正方体拼成一个长方体,这个长方体的表面积是( )平方厘米。
12.一个用立方块搭成的立体图形,小明从前面看到的图形是,从上面看是,那么搭成这样一个立体图形最少要( )个小立方块。
13.80000cm3( )dm3=( )m3 0.001m3=( )dm3=( )cm3
14.下面图形是由棱长为1厘米的小正方体搭拼成的,它的表面积是____平方厘米;至少还需要____ 个这样的小正方体,才能搭拼成棱长为3厘米的一个正方体。
15.棱长是2分米的正方体棱长总和是_______分米,表面积是_______平方分米。
16.一个长方体纸箱,长5分米,宽3分米,高4分米,它所有的棱长的和是 ( )分米,占地面积是( )平方分米,做这样一个纸箱需要纸板( )平方分米,它的体积是( )立方分米。
三、图形计算
17.计算下列图形的表面积和体积。(单位:dm)
四、解答题
18.下图是一个正方体的展开图,如果把正方体相对两个面上的数字相加,得到的三个和中最小的是多少?
19.一个正方体的6个面上分别写着A、B、C、D、E、F,根据下面3种摆放情况,判断每个字母对面的字母分别是什么?
20.在长20cm,宽7cm的长方形的四个角上各剪去一个边长为1cm的小正方形,做一个无盖的纸盒,这个纸盒的体积是多少?
21.一个长方体木块,如图切成三块,中间的正方体木块比原长方体的表面积少96平方厘米,那么原来长方体的体积是多少立方厘米?
22.用彩带捆扎下面的礼品盒,需要多少厘米彩带?(彩带结长15厘米)
23.一个无盖玻璃鱼缸的形状是正方体,棱长是3分米,制作这个鱼缸至少需要多大面积的玻璃?这个鱼缸可以容水多少升?
24.一根铁丝长120cm,现将这根铁丝焊接成一个正方体的模型.这个正方体的体积是多少立方厘米?
25.把一个铁块放入一个长为40厘米,宽为15厘米的长方体水槽中,水面上升了3厘米,这个铁块的体积是多少立方厘米?
26.把三个完全相同的正方体摆成一个长方体,这个长方体的表面积是224平方厘米,每个正方体的表面积是多少平方厘米?
27.把一张长20厘米、宽12厘米的硬纸板,从四个角各剪去一个正方形,再折成一个高2厘米的长方体无盖纸盒。这个纸盒的容积是多少平方厘米?
试卷第1页,共3页
试卷第2页,共2页
参考答案:
1.B
【分析】一个无盖的正方体纸盒,下底标有字母“M”,沿图中粗线将其展开成平面图形,则是正方体展开图的“1-4-1”形中的“1-4”,且是右端对齐。据此可以解答。
【详解】有一个无盖的正方体纸盒,下底标有字母“M”,沿图中粗线将其展开成平面图形是:
故答案为:B
【点睛】此题考查正方体的表面展开图,需熟练掌握正方体表面展开图的特征。
2.C
【详解】【错误答案】A
【错因】 错以为此题中顶点处正方体拿走不影响表面积。
【改正】 C
【反思】正方体顶点处拿走一个正方体,不影响表面积,拿走多个应具体分析,此题减少左右两个面的面积。
3.A
【分析】如图,这个正方体礼品盒中,其对面图案都相同,图A折叠成正方体礼盒后,心与心相对,笑脸与笑脸相对,太阳与太阳相对;图B折叠成正方体礼盒后,心与太阳相对,笑脸与笑脸相对;图C折叠成正方体礼盒后,心与心相对,笑脸与太阳相对;图D折叠成正方体礼盒后,心与笑脸相对,太阳与太阳相对.
【详解】根据分析,图A折叠成正方体礼盒后,心与心相对,笑脸与笑脸相对,太阳与太阳相对,即对面图案相同;
图B、图C和图D中对面图案不相同;
故选A.
4.B
【分析】观察图可知:最后得到的立方体图形的表面积=大正方体的表面积+两个小正方体4个侧面面积的和,将数值代入正方体表面积公式中计算即可。
【详解】最后得到的立方体图形的表面积:
42×6+22×4+12×4
=96+16+4
=116(平方厘米)
故答案为:B
【点睛】本题考查正方体表面积公式的应用,关键要理解求得是哪几个面的面积和。
5.B
【解析】略
6.C
【分析】由题意知:正方体的木料,它的底面积是10平方厘米,它的其余的面的面积也是10平方厘米。横截成4段后,增加了6个面。据此解答。
【详解】6×10=60(平方厘米)
故答案为:C
【点睛】理解横截成4段,增加6个面的表面积是解答本题的关键。
7.B
【解析】略
8.B
【详解】略
9.3
【分析】根据长方体的棱长公式:(长+宽+高)×4,已知长方体的长、宽和总棱长求高,代入公式,即可解答。
【详解】520÷4-60-40
=130-60-40
=70-40
=30(厘米)
30厘米=3分米
【点睛】本题考查长方体的特点,根据长方体的特点进行解答,注意单位换算。
10.18
【详解】以长为边最多放7÷2=3(块)……1(分米)
以宽为边最多放4÷2=2(块)
以高为边最多放6÷2=3(块)
所以:3×2×3=18(块)
【点睛】长方体里放木块应根据实际情况,先求出每条棱长上最多能放的块数,再借助长方体的体积公式进行计算。
11.40
【分析】把两个棱长为2厘米的正方体拼成一个长方体,长方体的表面积比原来2个正方体的面积减少2个面的面积,据此解答。
【详解】2×2×(6×2-2)
=4×10
=40(平方厘米)
【点睛】考查了立体图形的切拼,此题也可以通过分析出长方体的长、宽、高,根据长方体的面积公式解答。
12.5
【分析】从前面看该立体图形有两层,下层3个,上层中间1个;上面看该立体图形有两行,上行中间1个,下行3个;所以搭成这样一个立体图形最少要5个小立方块。据此解答。
【详解】由分析可得:搭成这样一个立体图形最少要5个小立方块。
【点睛】根据视图求立体图形最多最少问题,从上面看的图形入手,分别标出每个位置的正方体个数。
13. 80 0.08 1 1000
【分析】将立方厘米换算成立方分米,除以进率1000,换算成立方米,除以进率1000000;
将立方米换算成立方分米,乘进率1000,换算成立方厘米,乘进率1000000。
【详解】80000cm3=80dm3=0.08 m3
0.001m3=1dm3=1000 cm3
【点睛】本题考查单位换算,牢记大单位换算小单位乘进率,小单位换算大单位除以进率。
14. 18 23
【分析】观察图形可知:从上面和下面看:分别有3个小正方体的面;从左面和右面看:分别有3个小正方体的面;从前面和后面看分别有3个小正方体的面,1个小正方体的面的面积是1×1=1平方厘米,由此即可求出这个图形的表面积;
拼组后的大正方体的每条棱长是由3个小正方体组成的,由此可以求出拼组后的大正方体中的小正方体的个数,再减去图中已有的小正方体个数即可。
【详解】3×6=18(平方厘米)
3×3×3-4
=27-4
=23(个)
【点睛】考查了立体图形的切拼,也考查了学生通过观察立体图形解决问题的能力。
15. 24 24
【分析】正方体棱长总和=棱长×12;正方体表面积=棱长×棱长×6;由此列式解答。
【详解】棱长总和:2×12=24(分米)
表面积:2×2×6
=4×6
=24(平方分米)
【点睛】题主要考查正方体的特征以及棱长总和与表面积的计算方法,直接利用公式解答即可。
16. 48 15 94 60
【分析】棱长之和=(长+宽+高)×4;占地面积=长×宽;长方体的表面积=(长×宽+长×高+宽×高)×2;长方体的体积=长×宽×高,代入数据计算即可。
【详解】(5+3+4)×4
=12×4
=48(分米)
它所有的棱长的和是48分米;
5×3=15(平方分米)
占地面积是15平方分米;
(5×3+5×4+3×4)×2
=(15+20+12)×2
=47×2
=94(平方分米)
做这样一个纸箱需要纸板94平方分米;
5×3×4=60(立方分米)
它的体积是60立方分米。
【点睛】此题考查了长方体的综合应用,掌握其棱长总和、体积和表面积的计算公式,认真计算即可。
17.220dm2;192dm3
【分析】对题中立体图形进行平移填补可知:该立体图形的表面积即是长10dm,宽5dm,高4分米的长方体的表面积,根据长方体表面积=(长×宽+长×高+宽×高)×2,代入数值计算;该立体图形的体积=大长方体体积-小立方体的体积,代入数值计算即可。
【详解】表面积:
(10×5+10×4+5×4)×2
=110×2
=220(dm2)
体积:
10×5×4-2×2×2
=200-8
=192(dm3)
18.4
【分析】符合正方体展开图的“3-3”型,折叠后,1对3;2对5;4对6;再把对应的两个数相加,即可判断最小的几,据此解答。
【详解】根据正方体展开图可知,1对3;2对5;4对6
1+3=4
2+5=7
4+6=10
4<7<10
最小的和是4
答:得到的三个和中最小的是4。
【点睛】本题考查正方体表面展开图,根据折叠后面的对应的数字,进行解答。
19.A对面为C;B对面为D;E对面为F
【分析】结合3种摆放情况,用排除法找对立面,据此解答。
【详解】由(1)(3)得A对面不可能是B、E、D、F,所以A对面为C。
由(1)(2)得B对面不可能是A、E、C、F,所以B对面为D。
则E对面为F。
【点睛】考查了立体图形找对立面的方法,学生应掌握。
20.90 cm3
【详解】7-1×2=5(cm)
20-1×2=18(cm)
18×5×1=90(cm3)
答:这个纸盒的体积是90 cm3。
21.360立方厘米
【分析】根据题意可知,减少的面积,就是上面长方体4个侧面面积和下面长方体4个侧面积面积,根据中间是正方体,上面的长方体的长和宽和下面的长方体的长和宽都等于正方体的棱长,用96除以4,就是高为3厘米和高为1厘米的长方体侧面的和,长和宽相等,进而求出这个长方体的长和宽,高等于3厘米+长方体的长+1厘米,根据长方体的体积公式:长×宽×高,即可解答。
【详解】96÷4=24(平方厘米)
长:24÷(3+1)
=24÷4
=6(厘米)
长方体的长是6厘米,宽是6厘米,高是3+6+1=10厘米
体积:6×6×10
=36×10
=360(立方厘米)
答:原来这个长方体的体积是360立方厘米。
【点睛】本题考查长方体体积公式的应用,关键是减少的面积是上面长方体4个侧面积和下面长方体4个侧面之和。
22.147厘米
【分析】仔细观察发现,六个面上与长相等的彩带有2段,长度为12厘米的彩带有6段,据此算出各段的长度再加上打结处的长度即可。
【详解】30×2+12×6
=60+72
=132(厘米)
132+15=147(厘米)
答:需要147厘米彩带。
【点睛】分别找出与长、宽、高相等的彩带段数。
23.45平方分米;27升
【分析】由于鱼缸无盖,所以只求它的5个面的总面积,根据正方形的面积公式:S=a2,求出一个面的面积再乘5即可求出制作这个鱼缸至少需要玻璃的面积;根据正方体的体积=棱长×棱长×棱长求出这个鱼缸以容水的升数。
【详解】3×3×5
=9×5
=45(平方分米)
答:制作这个鱼缸至少需要45平方分米的玻璃。
3×3×3
=9×3
=27(立方分米)
27立方分米=27升
答:这个鱼缸可以容水27升。
【点睛】考查了正方体表面积和体积的灵活应用,学生应掌握。
24.1000立方厘米
【详解】略
25.1800立方厘米
【分析】水面上生的体积就是铁块体积,用长×宽×水面上升的高度即可。
【详解】40×15×3=1800(立方厘米)
答:这个铁块的体积是1800立方厘米。
【点睛】关键是利用转化思想,将求不规则物体的体积转化为求长方体等规则物体的体积。
26.96平方厘米
【分析】3个正方体共有6×3=18个面,摆成一个长方体现在少了4个面,所以长方体是18-4=14个正方形的面,则一个面的面积是224÷14=16平方厘米,再乘6即可。如下图所示:
【详解】6×3=18(个)
18-4=14(个)
224÷14=16(平方厘米)
16×6=96(平方厘米)
答:每个正方体的表面积是96平方厘米。
【点睛】理清摆成一个长方体后有14个正方形的面是解题的关键。
27.256立方厘米
【详解】20-2×2=16(厘米)
12-2×2=8(厘米)
16×8×2=256(立方厘米)
答:这个纸盒的容积是256平方厘米。
答案第1页,共2页
答案第1页,共2页
