数学人教A版(2019)必修第一册3.2.2奇偶性 课件(共33张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册3.2.2奇偶性 课件(共33张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-23 07:21:41 | ||
图片预览







文档简介
(共33张PPT)
第三章 函数的概念与性质
3.2.2 奇偶性
学习目标
通过具体实例,理解奇函数、偶函数的定义
01
掌握奇函数、偶函数图像的特征
02
会用定义法和图像法判断函数奇偶性
03
轴对称图形:
如果一个图形上的任意一点关于某一条直线的对称点仍是这个图形上的点,就称图形关于该直线成轴对称,这条直线称作该轴对称图形的对称轴. (把图形沿对称轴对折,对称轴两侧的图形完全重合)
中心对称图形:
如果一个图形上的任意一点关于某一点的对称点仍是这个图形上的点,就称图形关于该点成中心对称,这个点称作该中心对称图形的对称中心.(把图形沿对称中心旋转180o,旋转后与原来的图形完全重合)
前面我们用符号语言精确地描述了函数图像在定义域的某个区间上“上升”(或“下降”)的性质,下面我们研究函数的其他性质.
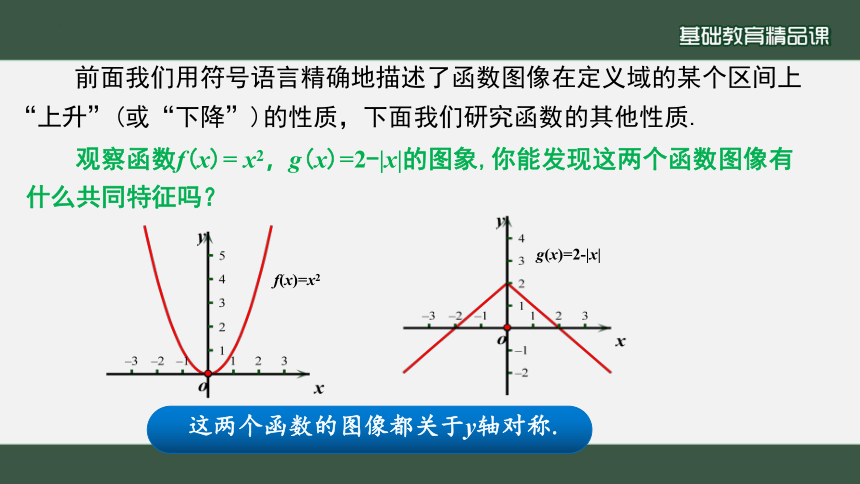
观察函数f(x)= x2,g(x)=2-|x|的图象,你能发现这两个函数图像有什么共同特征吗?
f(x)=x2
g(x)=2-|x|
这两个函数的图像都关于y轴对称.
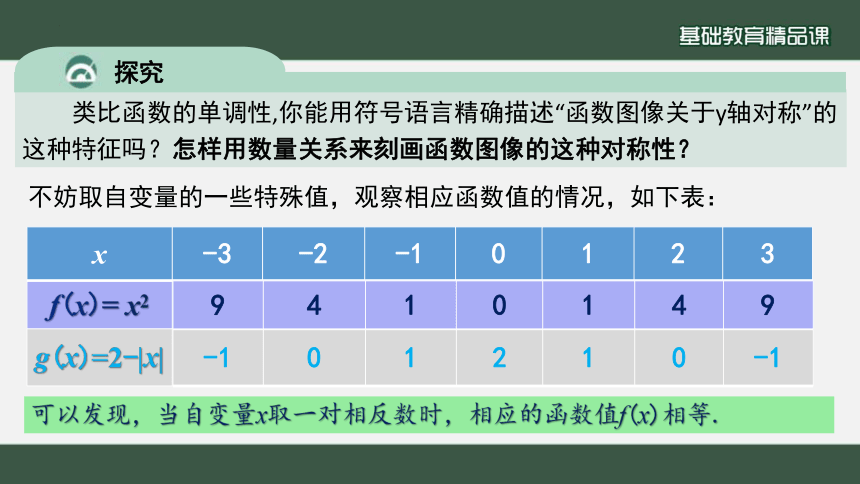
x -3 -2 -1 0 1 2 3
f(x)= x2
g(x)=2-|x|
不妨取自变量的一些特殊值,观察相应函数值的情况,如下表:
可以发现,当自变量x取一对相反数时,相应的函数值f(x)相等.
9 4 1 0 1 4 9
-1 0 1 2 1 0 -1
类比函数的单调性,你能用符号语言精确描述“函数图像关于y轴对称”的这种特征吗?怎样用数量关系来刻画函数图像的这种对称性?
探究
例如,对于函数f(x)= x2,有:
实际上,对于 x∈R,都有:
f(-x) = f(x)
这时候,我们称函数f(x)= x2为偶函数.
对于函数g(x)= 2-|x|,有:
实际上,对于 x∈R,都有:
g(-x)=g(x)
我们称函数g(x)= 2-|x|为 偶函数.
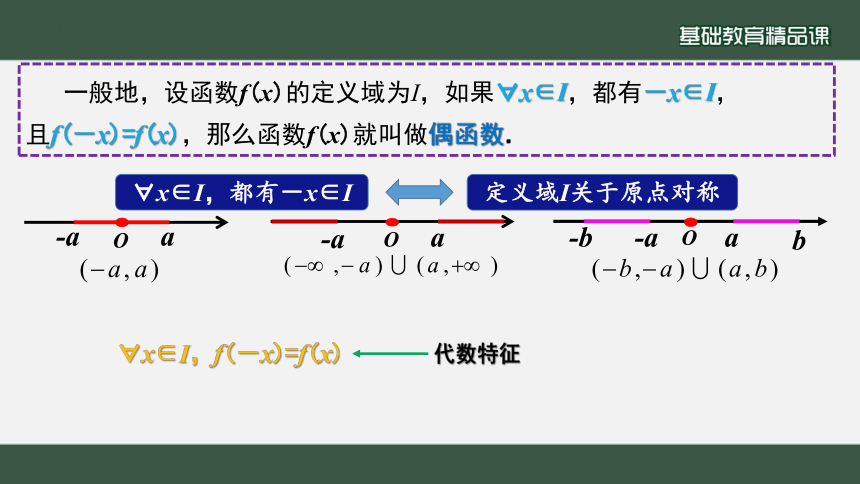
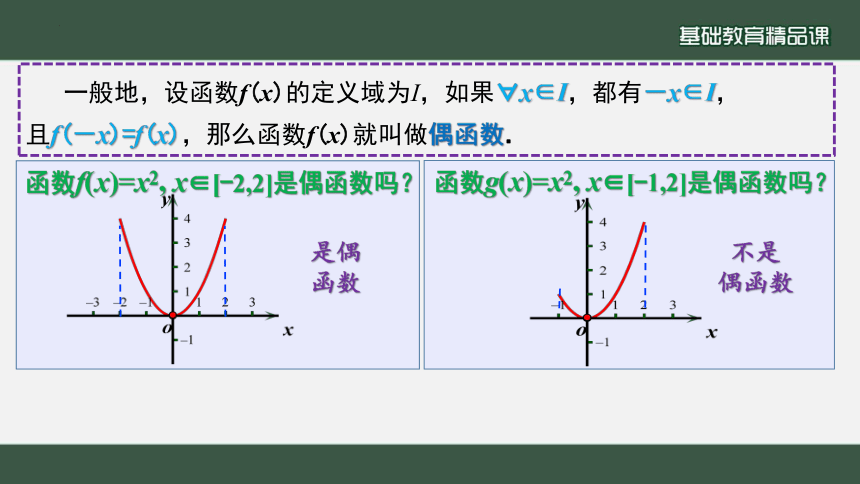
一般地,设函数f(x)的定义域为I,如果 x∈I,都有-x∈I,
且f(-x)=f(x),那么函数f(x)就叫做偶函数.
x∈I,f(-x)=f(x)
代数特征
x∈I,都有-x∈I
定义域I关于原点对称
-a
a
O
O
-a
a
O
a
-a
b
-b
函数f(x)=x2, x∈[-2,2]是偶函数吗?
函数g(x)=x2, x∈[-1,2]是偶函数吗?
是偶函数
不是偶函数
一般地,设函数f(x)的定义域为I,如果 x∈I,都有-x∈I,
且f(-x)=f(x),那么函数f(x)就叫做偶函数.
定义域关于原点对称
f(-x)=f(x)
偶函数 f(x)
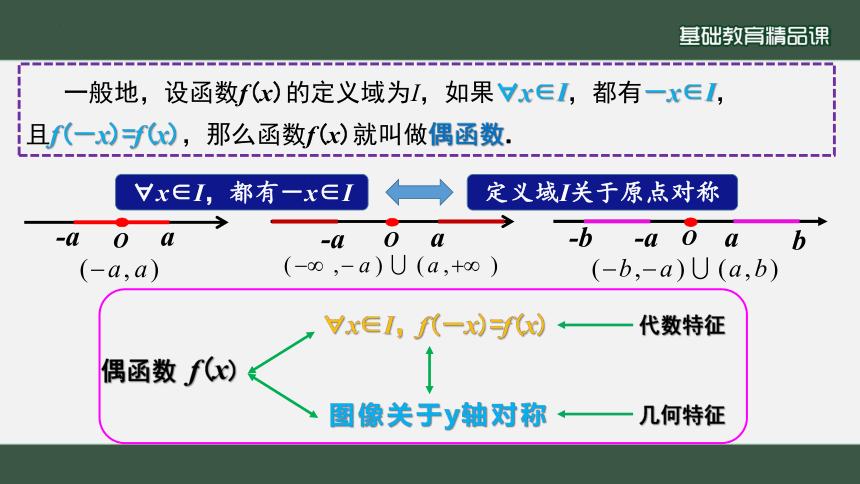
一般地,设函数f(x)的定义域为I,如果 x∈I,都有-x∈I,
且f(-x)=f(x),那么函数f(x)就叫做偶函数.
x∈I,f(-x)=f(x)
图像关于y轴对称
代数特征
几何特征
x∈I,都有-x∈I
定义域I关于原点对称
-a
a
O
O
-a
a
O
a
-a
b
-b
函数f(x)=x2, x∈[-2,2]是偶函数吗?
函数g(x)=x2, x∈[-1,2]是偶函数吗?
是偶函数
不是 偶函数
一般地,设函数f(x)的定义域为I,如果 x∈I,都有-x∈I,
且f(-x)=f(x),那么函数f(x)就叫做偶函数.
请同学们先结合课本第83页,通过独立思考,完成导学案探究二的1、2
再以小组讨论的形式讨论以下问题:
1、两个函数图像有什么共同特征?
2、从表格的数据中,你可以发现什么信息?
3、类比偶函数的定义,从奇函数的定义中,你可以发现奇函数的定义域有什么特征?奇函数的函数值有什么特征?
4、奇函数的图像有什么特征?
5、类比偶函数,满足什么条件的函数才能够称为奇函数?
探究
观察函数 的图象,你能发现这两个函数图像有什么共同特征吗?你能用符号语言精确描述这一特征吗?
这两个函数的图像都关于原点成中心对称.
x -3 -2 -1 0 1 2 3
f(x)= x
为了用数学符号语言描述这一特征,不妨取自变量的一些特殊值,
观察相应函数值的情况,如下表:
可以发现,当自变量x取一对相反数时,相应的函数值f(x)也是一对相反数.
-3 -2 -1 0 1 2 3
实际上,对于 x∈R,都有:
f(-x) = - f(x),
我们称函数f(x)= x为奇函数.
例如,对于函数f(x)= x,有:
对于函数 ,有:
对于 ,都有:
我们称函数 为奇函数.
一般地,设函数f(x)的定义域为I,如果 x∈I,都有-x∈I,且f(-x)=-f(x),那么函数f(x)就叫做奇函数.
x∈I,f(-x)= -f(x)
奇函数 f(x)
图像关于原点对称
代数特征
几何特征
x∈I,都有-x∈I
定义域I关于原点对称
函数f(x)=x, x∈[-2,2]是奇函数吗?
是奇函数
函数g(x)=x, x∈[-1,3]是奇函数吗?
不是 奇函数
思考1奇函数的定义域有什么特征?
定义域关于原点对称
思考2设函数y=f(x)是奇函数,且在x=0处有定义,则f(0)=
函数是奇函数或是偶函数称为函数的奇偶性,函数的奇偶性是在函数定义域内的整体性质;
由函数的奇偶性定义可知,函数具有奇偶性的一个必要条件是,对于定义域内的任意一个x,则-x也一定是定义域内的一个自变量(即定义域关于原点对称).
奇、偶函数定义的逆命题也成立,即
若f(x)为奇函数,则有f(-x)=-f(x)成立.
若f(x)为偶函数,则有f(-x)=f(x)成立.
×
×
×
×
3.函数y=f(x),x∈[-1,a](a>-1)是奇函数,则a等于( )
A.-1 B.0 C.1 D.无法确定
B
C
例1 用定义判断下列函数的奇偶性:
例1 判断下列函数的奇偶性:
例1 判断下列函数的奇偶性:
求函数f(x)的定义域
f(x)既不是奇函数也不是偶函数
判断f(-x)与f(x)的关系
判断定义域是否关于原点对称?
f(-x)≠ f(x)且f(-x)≠ - f(x)
是
否
f(-x)= f(x)
f(x)是偶函数
f(x)是奇函数
f(-x)= -f(x)
定义法判断函数奇偶性的步骤
f(x)既是奇函数 也是偶函数
f(-x)= f(x)= - f(x)
一个函数为奇函数 它的图象关于原点对称
一个函数为偶函数 它的图象关于y轴对称
判断函数的奇偶性,简化函数图象的画法
例2:
练习2
1.偶函数与奇函数的定义:
偶函数:设函数f (x)的定义域为I,如果 x∈I,都有-x∈I,且f(-x)=f(x),那么
函数f (x)就叫做偶函数.
奇函数:设函数f (x)的定义域为I,如果 x∈I,都有-x∈I,且f(-x)=-f(x),那么
函数f (x)就叫做奇函数.
2.判断函数奇偶性的方法:
(1)图象法: 偶函数图像关于y轴对称,奇函数关于原点对称;
(2)定义法: ①先求定义域,看是否关于原点对称;
②再判断f (-x)= - f (x)或f (-x)=f (x)是否恒成立;
③根据定义下结论.
(奇函数,偶函数,既不是奇函数也不是偶函数,既是奇函数也是偶函数)
学习目标
通过具体实例,理解奇函数、偶函数的定义
01
掌握奇函数、偶函数图像的特征
02
会用定义法和图像法判断函数奇偶性
03
达标检测:
利用函数奇偶性的定义求值
达标检测:
利用函数奇偶性的定义求值
达标检测:
利用函数奇偶性的定义求值
方法总结:
(1)定义域含参数:奇(偶)函数f(x)的定义域为[a,b],根据定义域关于原点对称,可以利用a+b=0求参数。
(2)解析式含参数:根据f(-x)=f(x)或f(-x)=-f(x)列式,比较系数可解。
利用函数奇偶性的定义求值
第三章 函数的概念与性质
3.2.2 奇偶性
学习目标
通过具体实例,理解奇函数、偶函数的定义
01
掌握奇函数、偶函数图像的特征
02
会用定义法和图像法判断函数奇偶性
03
轴对称图形:
如果一个图形上的任意一点关于某一条直线的对称点仍是这个图形上的点,就称图形关于该直线成轴对称,这条直线称作该轴对称图形的对称轴. (把图形沿对称轴对折,对称轴两侧的图形完全重合)
中心对称图形:
如果一个图形上的任意一点关于某一点的对称点仍是这个图形上的点,就称图形关于该点成中心对称,这个点称作该中心对称图形的对称中心.(把图形沿对称中心旋转180o,旋转后与原来的图形完全重合)
前面我们用符号语言精确地描述了函数图像在定义域的某个区间上“上升”(或“下降”)的性质,下面我们研究函数的其他性质.
观察函数f(x)= x2,g(x)=2-|x|的图象,你能发现这两个函数图像有什么共同特征吗?
f(x)=x2
g(x)=2-|x|
这两个函数的图像都关于y轴对称.
x -3 -2 -1 0 1 2 3
f(x)= x2
g(x)=2-|x|
不妨取自变量的一些特殊值,观察相应函数值的情况,如下表:
可以发现,当自变量x取一对相反数时,相应的函数值f(x)相等.
9 4 1 0 1 4 9
-1 0 1 2 1 0 -1
类比函数的单调性,你能用符号语言精确描述“函数图像关于y轴对称”的这种特征吗?怎样用数量关系来刻画函数图像的这种对称性?
探究
例如,对于函数f(x)= x2,有:
实际上,对于 x∈R,都有:
f(-x) = f(x)
这时候,我们称函数f(x)= x2为偶函数.
对于函数g(x)= 2-|x|,有:
实际上,对于 x∈R,都有:
g(-x)=g(x)
我们称函数g(x)= 2-|x|为 偶函数.
一般地,设函数f(x)的定义域为I,如果 x∈I,都有-x∈I,
且f(-x)=f(x),那么函数f(x)就叫做偶函数.
x∈I,f(-x)=f(x)
代数特征
x∈I,都有-x∈I
定义域I关于原点对称
-a
a
O
O
-a
a
O
a
-a
b
-b
函数f(x)=x2, x∈[-2,2]是偶函数吗?
函数g(x)=x2, x∈[-1,2]是偶函数吗?
是偶函数
不是偶函数
一般地,设函数f(x)的定义域为I,如果 x∈I,都有-x∈I,
且f(-x)=f(x),那么函数f(x)就叫做偶函数.
定义域关于原点对称
f(-x)=f(x)
偶函数 f(x)
一般地,设函数f(x)的定义域为I,如果 x∈I,都有-x∈I,
且f(-x)=f(x),那么函数f(x)就叫做偶函数.
x∈I,f(-x)=f(x)
图像关于y轴对称
代数特征
几何特征
x∈I,都有-x∈I
定义域I关于原点对称
-a
a
O
O
-a
a
O
a
-a
b
-b
函数f(x)=x2, x∈[-2,2]是偶函数吗?
函数g(x)=x2, x∈[-1,2]是偶函数吗?
是偶函数
不是 偶函数
一般地,设函数f(x)的定义域为I,如果 x∈I,都有-x∈I,
且f(-x)=f(x),那么函数f(x)就叫做偶函数.
请同学们先结合课本第83页,通过独立思考,完成导学案探究二的1、2
再以小组讨论的形式讨论以下问题:
1、两个函数图像有什么共同特征?
2、从表格的数据中,你可以发现什么信息?
3、类比偶函数的定义,从奇函数的定义中,你可以发现奇函数的定义域有什么特征?奇函数的函数值有什么特征?
4、奇函数的图像有什么特征?
5、类比偶函数,满足什么条件的函数才能够称为奇函数?
探究
观察函数 的图象,你能发现这两个函数图像有什么共同特征吗?你能用符号语言精确描述这一特征吗?
这两个函数的图像都关于原点成中心对称.
x -3 -2 -1 0 1 2 3
f(x)= x
为了用数学符号语言描述这一特征,不妨取自变量的一些特殊值,
观察相应函数值的情况,如下表:
可以发现,当自变量x取一对相反数时,相应的函数值f(x)也是一对相反数.
-3 -2 -1 0 1 2 3
实际上,对于 x∈R,都有:
f(-x) = - f(x),
我们称函数f(x)= x为奇函数.
例如,对于函数f(x)= x,有:
对于函数 ,有:
对于 ,都有:
我们称函数 为奇函数.
一般地,设函数f(x)的定义域为I,如果 x∈I,都有-x∈I,且f(-x)=-f(x),那么函数f(x)就叫做奇函数.
x∈I,f(-x)= -f(x)
奇函数 f(x)
图像关于原点对称
代数特征
几何特征
x∈I,都有-x∈I
定义域I关于原点对称
函数f(x)=x, x∈[-2,2]是奇函数吗?
是奇函数
函数g(x)=x, x∈[-1,3]是奇函数吗?
不是 奇函数
思考1奇函数的定义域有什么特征?
定义域关于原点对称
思考2设函数y=f(x)是奇函数,且在x=0处有定义,则f(0)=
函数是奇函数或是偶函数称为函数的奇偶性,函数的奇偶性是在函数定义域内的整体性质;
由函数的奇偶性定义可知,函数具有奇偶性的一个必要条件是,对于定义域内的任意一个x,则-x也一定是定义域内的一个自变量(即定义域关于原点对称).
奇、偶函数定义的逆命题也成立,即
若f(x)为奇函数,则有f(-x)=-f(x)成立.
若f(x)为偶函数,则有f(-x)=f(x)成立.
×
×
×
×
3.函数y=f(x),x∈[-1,a](a>-1)是奇函数,则a等于( )
A.-1 B.0 C.1 D.无法确定
B
C
例1 用定义判断下列函数的奇偶性:
例1 判断下列函数的奇偶性:
例1 判断下列函数的奇偶性:
求函数f(x)的定义域
f(x)既不是奇函数也不是偶函数
判断f(-x)与f(x)的关系
判断定义域是否关于原点对称?
f(-x)≠ f(x)且f(-x)≠ - f(x)
是
否
f(-x)= f(x)
f(x)是偶函数
f(x)是奇函数
f(-x)= -f(x)
定义法判断函数奇偶性的步骤
f(x)既是奇函数 也是偶函数
f(-x)= f(x)= - f(x)
一个函数为奇函数 它的图象关于原点对称
一个函数为偶函数 它的图象关于y轴对称
判断函数的奇偶性,简化函数图象的画法
例2:
练习2
1.偶函数与奇函数的定义:
偶函数:设函数f (x)的定义域为I,如果 x∈I,都有-x∈I,且f(-x)=f(x),那么
函数f (x)就叫做偶函数.
奇函数:设函数f (x)的定义域为I,如果 x∈I,都有-x∈I,且f(-x)=-f(x),那么
函数f (x)就叫做奇函数.
2.判断函数奇偶性的方法:
(1)图象法: 偶函数图像关于y轴对称,奇函数关于原点对称;
(2)定义法: ①先求定义域,看是否关于原点对称;
②再判断f (-x)= - f (x)或f (-x)=f (x)是否恒成立;
③根据定义下结论.
(奇函数,偶函数,既不是奇函数也不是偶函数,既是奇函数也是偶函数)
学习目标
通过具体实例,理解奇函数、偶函数的定义
01
掌握奇函数、偶函数图像的特征
02
会用定义法和图像法判断函数奇偶性
03
达标检测:
利用函数奇偶性的定义求值
达标检测:
利用函数奇偶性的定义求值
达标检测:
利用函数奇偶性的定义求值
方法总结:
(1)定义域含参数:奇(偶)函数f(x)的定义域为[a,b],根据定义域关于原点对称,可以利用a+b=0求参数。
(2)解析式含参数:根据f(-x)=f(x)或f(-x)=-f(x)列式,比较系数可解。
利用函数奇偶性的定义求值
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
