沪教版(上海)九下 第二十八章统计初步专项攻克试题(名师精选,含解析)
文档属性
| 名称 | 沪教版(上海)九下 第二十八章统计初步专项攻克试题(名师精选,含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-23 16:21:38 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
九年级数学第二学期第二十八章统计初步专项攻克
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相 ( http: / / www.21cnjy.com )应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。21教育网
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、在一次班级体测调查中, ( http: / / www.21cnjy.com )收集到40名同学的跳高数据,数据分别落在5个组内,且落入第一、二、三、五组的数据个数分别为2、7、11、12,则第四组频数为( ).
A.9 B.8 C.7 D.6
2、小明抛一枚硬币100次,其中有60次正面朝上,则反面朝上的频率是( )
A.0.6 B.6 C.0.4 D.4
3、甲、乙、丙、丁四名跳高运动员最近 ( http: / / www.21cnjy.com )10次训练成绩的平均数与方差如表所示.根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择的是( )21*cnjy*com
甲 乙 丙 丁
平均数/m 180 180 185 185
方差 8.2 3.9 75 3.9
A.甲 B.乙 C.丙 D.丁
4、一组数据的最大值为105,最小值为23,若确定组距为9,则分成的组数为( )
A.11 B.10 C.9 D.8
5、下列问题不适合用全面调查的是( )
A.旅客上飞机前的安检 B.企业招聘,对应试人员进行面试
C.了解全班同学每周体育锻炼的时间 D.调查市场上某种食品的色素含量是否符合国家标准
6、下列调查中最适合采用全面调查的是( )
A.调查甘肃人民春节期间的出行方式 B.调查市场上纯净水的质量
C.调查我市中小学生垃圾分类的意识 D.调查某航班上的乘客是否都持有“绿色健康码”
7、某校“安全知识”比赛有16 ( http: / / www.21cnjy.com )名同学参加,规定前8名的同学进入决赛.若某同学想知道自己能否晋级,不仅要了解自己的成绩,还需要了解16名参赛同学成绩的( )
A.平均数 B.中位数 C.众数 D.方差
8、下列调查中,最适合采用抽样调查的是( )
A.调查一批防疫口罩的质量
B.调查某校九年级学生的视力
C.对乘坐某班次飞机的乘客进行安检
D.国务院于2020年11月1日开展的第七次全国人口调查
9、为了解学生参加体育锻炼的情况、现将 ( http: / / www.21cnjy.com )九年级(1)班同学一周的体育锻炼情况绘制成如图所示不完整的条形统计图,已知锻炼7小时的人数占全班总人数的20%,则下列结论正确的是( )
( http: / / www.21cnjy.com / )
A.九年级(1)班共有学生40名 B.锻炼时间为8小时的学生有10名
C.平均数是8.5小时 D.众数是8小时
10、甲、乙、丙、丁四名学生近4次数 ( http: / / www.21cnjy.com )学测验成绩的平均数都是90分,方差分别是S甲2=5,S乙2=20,S丙2=23,S丁2=32,则这四名学生的数学成绩最稳定的是( )2·1·c·n·j·y
A.甲 B.乙 C.丙 D.丁
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、已知一组数据:18,17,13,15,17,16,14,17,则这组数据的中位数与众数分别是__________.
2、如图为某市未来几天的每日最高气温与最低气温的变化趋势图,根据图中信息可知,最大的温差是______.
( http: / / www.21cnjy.com / )
3、八年级(1)、(2)两班人数相同,在同一次数学单元测试中,班级平均分和方差如下:则成绩较为稳定的班级是___.
4、跳远运动员李强在一次训练中,先跳了6次的成绩如下:7.6,7.8,7.7,7.8,8.0,7.9(单位:m).这六次成绩的平均数为7.8,方差为.如果李强再跳两次,成绩分别为7.6,8.0,则李强这8次跳远成绩与前6次的成绩相比较,其方差 _____.(填“变大”、“不变”或“变小”)
5、小王参加某企业招聘测试,他的笔试、面试 ( http: / / www.21cnjy.com )、技能操作得分分别为80分、85分、90分,若依次按照2:3:5的比例确定成绩,则小王的成绩是_____.
三、解答题(5小题,每小题10分,共计50分)
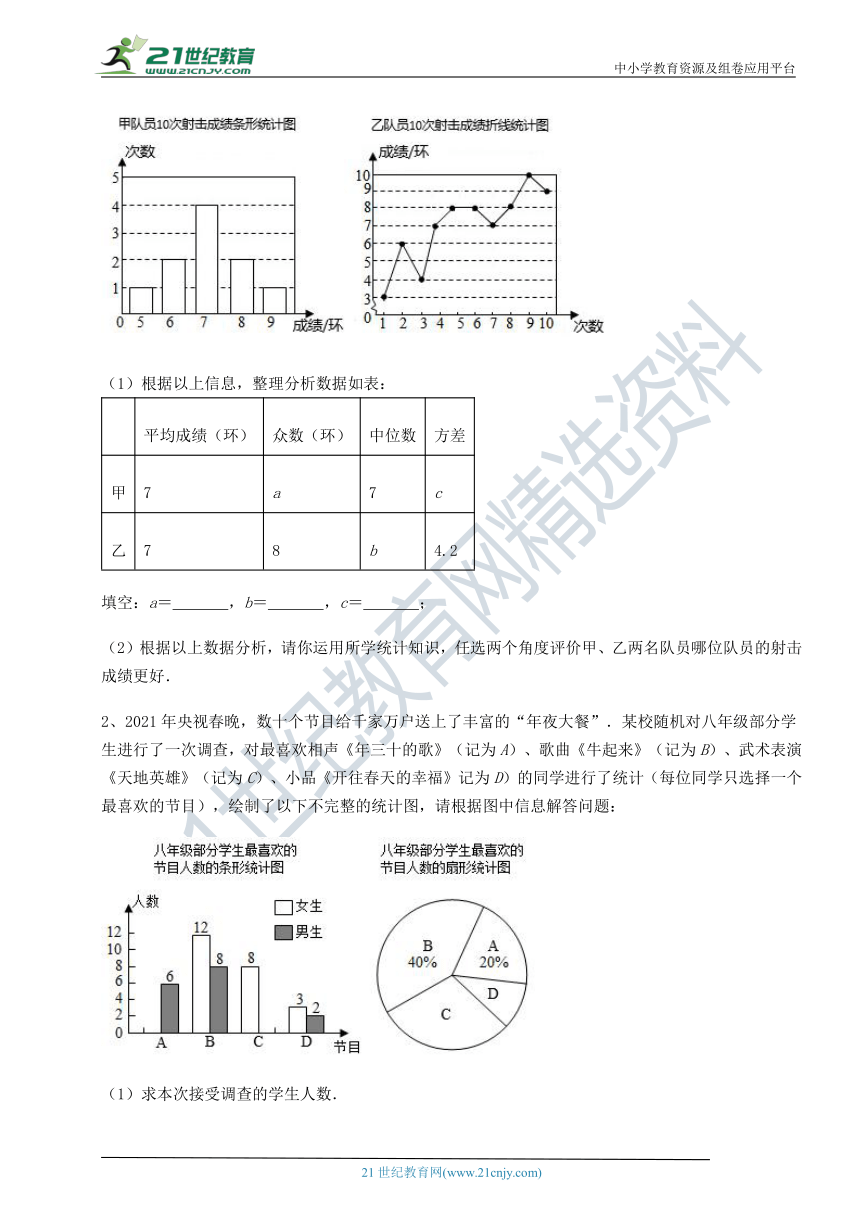
1、甲、乙两名队员参加射击训练,将10次成绩分别制成如图所示的两个统计图:
( http: / / www.21cnjy.com / )
(1)根据以上信息,整理分析数据如表:
平均成绩(环) 众数(环) 中位数 方差
甲 7 a 7 c
乙 7 8 b 4.2
填空:a= ,b= ,c= ;
(2)根据以上数据分析,请你运用所学统计知识,任选两个角度评价甲、乙两名队员哪位队员的射击成绩更好.【来源:21cnj*y.co*m】
2、2021年央视春晩,数十个节目 ( http: / / www.21cnjy.com )给千家万户送上了丰富的“年夜大餐”.某校随机对八年级部分学生进行了一次调查,对最喜欢相声《年三十的歌》(记为A)、歌曲《牛起来》(记为B)、武术表演《天地英雄》(记为C)、小品《开往春天的幸福》记为D)的同学进行了统计(每位同学只选择一个最喜欢的节目),绘制了以下不完整的统计图,请根据图中信息解答问题:
( http: / / www.21cnjy.com / )
(1)求本次接受调查的学生人数.
(2)求扇形统计图中D所在扇形的圆心角度数.
(3)将条形统计图补充完整.
3、为迎接中国共产党建党100周年,綦 ( http: / / www.21cnjy.com )江区某中学组织开展了丰富多彩的系列庆祝活动.学习了解党的历史是其中一项重要的活动.为了解七、八年级学生(七、八年级各有500名学生)的学习效果,该校举行了党史知识竞赛.现从两个年级各随机抽取20名学生的竞赛成绩(百分制)进行分析,过程如下:
一、收集数据:
七年级:79,89,78,85,80,81,92,75,80,99,80,84,86,81,80,85,91,65,88,82
八年级:97,85,92,87,77,86,99,88,76,88,85,82,80,86,77,82,87,85,75,46
二、整理数据:
40≤x<50 50≤x<60 60≤x<70 70≤x<80 80≤x<90 90≤x<100
七年级 0 0 1 3 13 3
八年级 1 0 0 a b 3
三、分析数据:
平均数 众数 中位数
七年级 83 c 81.5
八年级 83 85 85
应用数据:
(1)由上表填空:a= ,b= ,c= .
(2)估计该校七、八两个年级学生在本次竞赛中成绩在80分以上(含80分)的共有多少人?
(3)你认为哪个年级的学生对党的知识掌握的总体水平较好,请说明理由.
4、某校学生会为了解该校2860名学 ( http: / / www.21cnjy.com )生喜欢球类活动的情况,采取抽样调查的办法,从足球、乒乓球、篮球、排球等四个方面调查了若干名学生的兴趣爱好,并将调查的结果绘制成右边的两幅不完整的统计图(如图(1),图(2),要求每位同学只能选择一种自己喜欢的球类;图中用乒乓球、足球、排球、篮球代表喜欢这四种球类中的某一种球类的学生人数),请你根据图中提供的信息,解答下列问题:【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com / )
(1)在这次研究中,一共调查了 名学生.
(2)喜欢排球的人数在扇形统计图中所占的圆心角是 度.
(3)补全频数分布折线统计图.
(4)估计该校喜欢排球的学生有多少人?
5、某校想了解学生每周的课外阅读时间情况,随机抽取了部分学生进行调查,对学生每周的课外阅读时间(单位:小时)进行分组整理,并绘制了如图所示的不完整的频数分布直方图和扇形统计图:
( http: / / www.21cnjy.com / )
根据以上信息,解答下列问题:
(1)本次调查共随机抽取了_____________名学生,并补全频数分布直方图;
(2)求扇形统计图中m的值和E组对应的圆心角度数;
(3)在该校3000名学生中,每周的课外阅读时间不小于6小时的学生约有________________名.
-参考答案-
一、单选题
1、B
【分析】
根据题意可得:共40个数据,知道一、二、三、五组的数据个数,用总数减去这几组频数,即可得到答案.
【详解】
解:由题意得:第四组的频数=40-(2+7+11+12)=8;
故选B.
【点睛】
本题是对频数的考查,掌握各小组频数之和等于数据总和是解题的关键.
2、C
【分析】
先求出反面朝上的频数,然后根据频率=频数÷总数求解即可
【详解】
解:∵小明抛一枚硬币100次,其中有60次正面朝上,
∴小明抛一枚硬币100次,其中有40次反面朝上,
∴反面朝上的频率=40÷100=0.4,
故选C.
【点睛】
本题主要考查了根据频数求频率,解题的关键在于能够熟练掌握频率=频数÷总数.
3、D
【分析】
首先比较平均数,平均数相同时选择方差较小的运动员参加.
【详解】
解:∵,
∴从丙和丁中选择一人参加比赛,
∵S丙2>S丁2,
∴选择丁参赛,
故选:D.
【点睛】
此题考查了平均数和方差,正确理解方差与平均数的意义是解题关键.
4、B
【分析】
极差除以组距,大于或等于该值的最小整数即为组数.
【详解】
解:,
分10组.
故选:B.
【点睛】
本题考查了组距的划分,一般分为组最科学.
5、D
【分析】
由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似,根据以上逐项分析可知.21·世纪*教育网
【详解】
解:A. 旅客上飞机前的安检,人员不多,且这个调查很重要不可漏掉任何人,适合全面调查,不符合题意, 【出处:21教育名师】
B. 企业招聘,对应试人员进行面试,人员不多,且这个调查很重要不可漏掉任何人,适合全面调查,不符合题意,21教育名师原创作品
C. 了解全班同学每周体育锻炼的时间,人员不多,适合全面调查,不符合题意,
D. 调查市场上某种食品的色素含量是否符合国家标准,调查具有破坏性,不适合全面调查,符合题意
故选D
【点睛】
本题考查的是全面调查与抽样调查,在调查实际生 ( http: / / www.21cnjy.com )活中的相关问题时,要灵活处理,既要考虑问题本身的需要,又要考虑实现的可能性和所付出代价的大小.理解全面调查与抽样调查的适用范围是解题的关键.21·cn·jy·com
6、D
【分析】
根据抽样调查和全面调查的定义逐一判断即可.
【详解】
解|:A、调查甘肃人民春节期间的出行方式,应采用抽样调查,故不符合题意;
B、调查市场上纯净水的质量,应采用抽样调查,故不符合题意;
C、调查我市中小学生垃圾分类的意识,应采用抽样调查,故不符合题意;
D、调查某航班上的乘客是否都持有“绿色健康码”,应采用全面调查,故符合题意;
故选D.
【点睛】
本题考查了抽样调查和全面调查 ( http: / / www.21cnjy.com )的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
7、B
【分析】
由中位数的概念,即最中间一个或两个数据 ( http: / / www.21cnjy.com )的平均数;可知16人成绩的中位数是第8名和第9名的成绩.根据题意可得:参赛选手要想知道自己是否能进入前8名,只需要了解自己的成绩以及全部成绩的中位数,比较即可.
【详解】
解:由于16个人中,第8和第9名的成绩的平 ( http: / / www.21cnjy.com )均数是中位数,故同学知道了自己的分数后,想知道自己能否进入决赛,还需知道这16位同学的成绩的中位数.
故选:B.
【点睛】
此题主要考查统计的有关知识,主要包括 ( http: / / www.21cnjy.com )平均数、中位数、众数的意义.反映数据集中程度的统计量有平均数、中位数、众数等,各有局限性,因此要对统计量进行合理的选择和恰当的运用.
8、A
【分析】
根据抽样调查和普查的定义进行求解即可.
【详解】
解:A.调查一批防疫口罩的质量,适合抽样调查,故选项符合题意;
B.调查某校九年级学生的视力,适合全面调查,故选项不符合题意;
C.对乘坐某班次飞机的乘客进行安检,适合全面调查,故选项不符合题意;
D.国务院于2020年11月1日开展的第七次全国人口调查,适合全面调查,故选项不符合题意;
故选A.
【点睛】
本题考查了抽样调查和全面调查 ( http: / / www.21cnjy.com )的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.www.21-cn-jy.com
9、D
【分析】
根据频数之和等于总数,频数定义,加权平均数的计算,众数的定义逐项判断即可求解.
【详解】
解:A. 九年级(1)班共有学生10+20+15+5=50名,故原选项判断错误,不合题意;
B. 锻炼时间为8小时的学生有20名,故原选项判断错误,不合题意;
C. 平均数是小时,故原选项判断错误,不合题意;
D. 众数是8小时,故原选项判断正确,符合题意.
故选:D
【点睛】
本题考查了频数、加权平均数、众数等知识,理解相关概念,看到条形图是解题关键.
10、A
【分析】
根据方差的意义求解即可.
【详解】
解:∵S甲2=5,S乙2=20,S丙2=23,S丁2=32,
∴S甲2<S乙2<S丙2<S丁2,
∴这四名学生的数学成绩最稳定的是甲,
故选:A.
【点睛】
本题主要考查了方差,方差是反映一组数据的波 ( http: / / www.21cnjy.com )动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越差;反之,则它与其平均值的离散程度越小,稳定性越好.【版权所有:21教育】
二、填空题
1、16.5,17
【分析】
根据众数和中位数的定义求解即可,中 ( http: / / www.21cnjy.com )位数:将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数.如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.众数:在一组数据中出现次数最多的数.
【详解】
将,,,,,,,从小到大排列为:,,,,,,,
其中出现的次数最多,则众数为,
中位数为:.
故答案为:;
【点睛】
本题考查了求众数和中位数,理解众数和中位数的定义是解题的关键.
2、10
【分析】
求出每天的最高气温与最低气温的差,再比较大小即可.
【详解】
解:∵由折线统计图可知,
15日温差=4 ( 3)=7;
16日温差=4 ( 6)=10;
17日温差=2 ( 6)=8;
18日温差=2 ( 2)=4;
19日温差=1 ( 5)=6;
20日温差=1 ( 1)=2;
∴最大的温差是10.
故答案为:10.
【点睛】
本题考查了折线统计图的应用以及有理数的减法,掌握有理数减法法则是解答本题的关键.有理数减法法则:减去一个数,等于加上这个数的相反数.www-2-1-cnjy-com
3、甲班
【分析】
根据平均数相同,方差反应一组数据与平均数的离散程度越小说明比较稳定即可得出结论.
【详解】
解:∵两班的平均成绩相同,,根据方差反应一组数据与平均数的离散程度越小说明比较稳定,
∴成绩较为稳定的班级是甲班,
故答案为甲班.
【点睛】
本题考查平均数与方差,掌握平均数的求法与 ( http: / / www.21cnjy.com )方差的求法,熟练方差反应一组数据与平均数的离散程度,方差越大离散的程度越大,方差越小离散程度越小,越稳定,与整齐等是解题关键.
4、变大
【分析】
先由平均数的公式计算出李强第二次的平均数,再根据方差的公式进行计算,然后比较即可得出答案.
【详解】
解:∵李强再跳两次,成绩分别为7.6,8.0,
∴这组数据的平均数是,
∴这8次跳远成绩的方差是:
∵0.0225>,
∴方差变大;
故答案为:变大.
【点睛】
本题主要考查了平均数的计算和方差的计算,熟练掌握平均数和方差的计算是解答此题的关键.
5、86.5
【分析】
根据加权平均数的计算公式列出算式,再进行计算即可.
【详解】
解:根据题意得:
80×+85×+90×,
=16+25.5+45,
=86.5(分),
故答案为:86.5.
【点睛】
本题考查了加权平均数,解题的关键是掌握加权平均数的计算公式.
三、解答题
1、(1),,;(2)答案见解析.
【分析】
(1)分别根据平均数,方差,中位数的定义求解即可;
(2)从众数与中位数的角度分析,乙的射击成绩都比甲要高,从而可得结论.
【详解】
解:(1)由频数直方图可得:甲的成绩如下:
其中环出现了4次,所以众数是环,
环
由折线统计图可得:按从小到大排序为:
所以中位数为:.
故答案为:,,;
(2)从众数与中位数来看,乙的众数与中位数都比甲高,所以乙的射击成绩比甲的射击成绩要好一些.
【点睛】
本题考查的是平均数,众数,中位数,方差的含义,根据平均数,众数,中位数,方差下结论,掌握以上基础概念是解本题的关键.21*cnjy*com
2、(1)50人;(2)36°;(3)见解析
【分析】
(1)根据B的人数除以所占的百分比得到接受调查的学生人数;
(2)先求出D所占百分比,然后用360°×它所占百分比即可;
(3)先求出C所占百分比,再求出C的 ( http: / / www.21cnjy.com )人数,进而得出C中男生人数;用总人数乘A占的百分比得出A的人数进而得出A中女生人数,然后补全条形统计图即可;
【详解】
解:(1)根据题意得:(人)
答:本次接受调查的人数是50人;
(2)D占的百分比,
D所在的扇形圆心角的度数为;
(3)C占的百分比为1-(20%+40%+10%)=30%,
C的人数为50×30%=15(人),即C中男生为15-8=7(人);
A的人数为50×20%=10(人),A中女生人数为10-6=4(人),
补全条形统计图,如图所示:
( http: / / www.21cnjy.com / )
【点睛】
本题考查的是条形统计图和扇形统计图的综合 ( http: / / www.21cnjy.com )运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.21世纪教育网版权所有
3、
(1)4,12,80
(2)775人
(3)八年级的学生对党史知识掌握的总体水平较好(答案不唯一,合理即可).
【分析】
(1)根据所收集的收据即可确定a、b的值,中位数是指一组数据中位于中间位置的数,假设数据中的总数为N,若N为奇数,中位数为第个数据;若样本数为偶数,中位数为第个数据和第数据的平均值,据此可确定C;21cnjy.com
(2)先分别求出七、八年级80分以上学生所占的百分比,然后列式计算即可;
(3)根据平均数、众数和中位数进行分析即可.
(1)
解:由题意知八年级70≤x<80共4人,80≤x<90共12人,
∴a=4,b=12,
∵七年级80分共有4人,
∴七年级成绩的众数80,
∴c=80,
故答案为:4,12,80;
(2)
解:该校七年级学生在本次竞赛中成绩在80分以上所占的百分比为16÷20×100%=80%
该校八年级学生在本次竞赛中成绩在80分以上所占的百分比为15÷20×100%=75%
所以估计该校七、八两个年级学生在本次竞赛中成绩在80分以上的共有500×80%+500×75%=775(人).2-1-c-n-j-y
(3)
解:八年级的总体水平较好,理由如下:
∵七、八年级的平均成绩相等,而八年级的中位数为85,七年级的中位数为81.5
85>81.5,
∴八年级得分高的人数相对较多,
∴八年级的学生对党史知识掌握的总体水平较好(答案不唯一,合理即可).
【点睛】
本题主要考查了数据的统计、求中位数以及运用中位数进行决策、用样本估计总体等知识点,正确的统计是基础、灵活应用相关知识是解答本题的关键.
4、(1)100;(2)36;(3)见解析;(4)286
【分析】
(1)用乒乓球的人数除以其百分比即可得到调查的学生数;
(2)先计算出喜欢篮球的人数,得到喜欢排球的人数,根据公式计算喜欢排球的人数在扇形统计图中所占的圆心角度数;
(3)根据(2)的数据补全统计图;
(4)用学校的总人数乘以喜欢排球的比例即可得到答案.
【详解】
解:调查的学生有(名),
故答案为:100;
(2)喜欢篮球的人数有(名),
喜欢排球的人数是100-30-20-40=10(名),
∴喜欢排球的人数在扇形统计图中所占的圆心角是,
故答案为:36;
(3)如图:
( http: / / www.21cnjy.com / )
(4)该校喜欢排球的学生有(人).
【点睛】
本题考查的是条形统计图和扇形统 ( http: / / www.21cnjy.com )计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
5、
(1)100,图见解析
(2),
(3)
【分析】
(1)组人数组所占百分比被调查总人数,将总人数组所占百分比组人数;
(2)组人数调查总人数,组对应的圆心角度数组占调查人数比例;
(3)将样本中课外阅读时间不小于6小时的百分比乘以3000可得.
(1)
解:(1)随机调查学生数为:(人,
课外阅读时间在小时之间的人数为:(人,
补全图形如下:
( http: / / www.21cnjy.com / )
故答案是:100;
(2)
解:,
组对应的圆心角为:;
(3)
解:(人.
估计该校3000名学生每周的课外阅读时间不小于6小时的人数约为870人,
故答案是:.
【点睛】
本题考查的是条形统计图和 ( http: / / www.21cnjy.com )扇形统计图的综合运用,解题的关键是读懂统计图,从不同的统计图中得到必要的信息,条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
九年级数学第二学期第二十八章统计初步专项攻克
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相 ( http: / / www.21cnjy.com )应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。21教育网
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、在一次班级体测调查中, ( http: / / www.21cnjy.com )收集到40名同学的跳高数据,数据分别落在5个组内,且落入第一、二、三、五组的数据个数分别为2、7、11、12,则第四组频数为( ).
A.9 B.8 C.7 D.6
2、小明抛一枚硬币100次,其中有60次正面朝上,则反面朝上的频率是( )
A.0.6 B.6 C.0.4 D.4
3、甲、乙、丙、丁四名跳高运动员最近 ( http: / / www.21cnjy.com )10次训练成绩的平均数与方差如表所示.根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择的是( )21*cnjy*com
甲 乙 丙 丁
平均数/m 180 180 185 185
方差 8.2 3.9 75 3.9
A.甲 B.乙 C.丙 D.丁
4、一组数据的最大值为105,最小值为23,若确定组距为9,则分成的组数为( )
A.11 B.10 C.9 D.8
5、下列问题不适合用全面调查的是( )
A.旅客上飞机前的安检 B.企业招聘,对应试人员进行面试
C.了解全班同学每周体育锻炼的时间 D.调查市场上某种食品的色素含量是否符合国家标准
6、下列调查中最适合采用全面调查的是( )
A.调查甘肃人民春节期间的出行方式 B.调查市场上纯净水的质量
C.调查我市中小学生垃圾分类的意识 D.调查某航班上的乘客是否都持有“绿色健康码”
7、某校“安全知识”比赛有16 ( http: / / www.21cnjy.com )名同学参加,规定前8名的同学进入决赛.若某同学想知道自己能否晋级,不仅要了解自己的成绩,还需要了解16名参赛同学成绩的( )
A.平均数 B.中位数 C.众数 D.方差
8、下列调查中,最适合采用抽样调查的是( )
A.调查一批防疫口罩的质量
B.调查某校九年级学生的视力
C.对乘坐某班次飞机的乘客进行安检
D.国务院于2020年11月1日开展的第七次全国人口调查
9、为了解学生参加体育锻炼的情况、现将 ( http: / / www.21cnjy.com )九年级(1)班同学一周的体育锻炼情况绘制成如图所示不完整的条形统计图,已知锻炼7小时的人数占全班总人数的20%,则下列结论正确的是( )
( http: / / www.21cnjy.com / )
A.九年级(1)班共有学生40名 B.锻炼时间为8小时的学生有10名
C.平均数是8.5小时 D.众数是8小时
10、甲、乙、丙、丁四名学生近4次数 ( http: / / www.21cnjy.com )学测验成绩的平均数都是90分,方差分别是S甲2=5,S乙2=20,S丙2=23,S丁2=32,则这四名学生的数学成绩最稳定的是( )2·1·c·n·j·y
A.甲 B.乙 C.丙 D.丁
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、已知一组数据:18,17,13,15,17,16,14,17,则这组数据的中位数与众数分别是__________.
2、如图为某市未来几天的每日最高气温与最低气温的变化趋势图,根据图中信息可知,最大的温差是______.
( http: / / www.21cnjy.com / )
3、八年级(1)、(2)两班人数相同,在同一次数学单元测试中,班级平均分和方差如下:则成绩较为稳定的班级是___.
4、跳远运动员李强在一次训练中,先跳了6次的成绩如下:7.6,7.8,7.7,7.8,8.0,7.9(单位:m).这六次成绩的平均数为7.8,方差为.如果李强再跳两次,成绩分别为7.6,8.0,则李强这8次跳远成绩与前6次的成绩相比较,其方差 _____.(填“变大”、“不变”或“变小”)
5、小王参加某企业招聘测试,他的笔试、面试 ( http: / / www.21cnjy.com )、技能操作得分分别为80分、85分、90分,若依次按照2:3:5的比例确定成绩,则小王的成绩是_____.
三、解答题(5小题,每小题10分,共计50分)
1、甲、乙两名队员参加射击训练,将10次成绩分别制成如图所示的两个统计图:
( http: / / www.21cnjy.com / )
(1)根据以上信息,整理分析数据如表:
平均成绩(环) 众数(环) 中位数 方差
甲 7 a 7 c
乙 7 8 b 4.2
填空:a= ,b= ,c= ;
(2)根据以上数据分析,请你运用所学统计知识,任选两个角度评价甲、乙两名队员哪位队员的射击成绩更好.【来源:21cnj*y.co*m】
2、2021年央视春晩,数十个节目 ( http: / / www.21cnjy.com )给千家万户送上了丰富的“年夜大餐”.某校随机对八年级部分学生进行了一次调查,对最喜欢相声《年三十的歌》(记为A)、歌曲《牛起来》(记为B)、武术表演《天地英雄》(记为C)、小品《开往春天的幸福》记为D)的同学进行了统计(每位同学只选择一个最喜欢的节目),绘制了以下不完整的统计图,请根据图中信息解答问题:
( http: / / www.21cnjy.com / )
(1)求本次接受调查的学生人数.
(2)求扇形统计图中D所在扇形的圆心角度数.
(3)将条形统计图补充完整.
3、为迎接中国共产党建党100周年,綦 ( http: / / www.21cnjy.com )江区某中学组织开展了丰富多彩的系列庆祝活动.学习了解党的历史是其中一项重要的活动.为了解七、八年级学生(七、八年级各有500名学生)的学习效果,该校举行了党史知识竞赛.现从两个年级各随机抽取20名学生的竞赛成绩(百分制)进行分析,过程如下:
一、收集数据:
七年级:79,89,78,85,80,81,92,75,80,99,80,84,86,81,80,85,91,65,88,82
八年级:97,85,92,87,77,86,99,88,76,88,85,82,80,86,77,82,87,85,75,46
二、整理数据:
40≤x<50 50≤x<60 60≤x<70 70≤x<80 80≤x<90 90≤x<100
七年级 0 0 1 3 13 3
八年级 1 0 0 a b 3
三、分析数据:
平均数 众数 中位数
七年级 83 c 81.5
八年级 83 85 85
应用数据:
(1)由上表填空:a= ,b= ,c= .
(2)估计该校七、八两个年级学生在本次竞赛中成绩在80分以上(含80分)的共有多少人?
(3)你认为哪个年级的学生对党的知识掌握的总体水平较好,请说明理由.
4、某校学生会为了解该校2860名学 ( http: / / www.21cnjy.com )生喜欢球类活动的情况,采取抽样调查的办法,从足球、乒乓球、篮球、排球等四个方面调查了若干名学生的兴趣爱好,并将调查的结果绘制成右边的两幅不完整的统计图(如图(1),图(2),要求每位同学只能选择一种自己喜欢的球类;图中用乒乓球、足球、排球、篮球代表喜欢这四种球类中的某一种球类的学生人数),请你根据图中提供的信息,解答下列问题:【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com / )
(1)在这次研究中,一共调查了 名学生.
(2)喜欢排球的人数在扇形统计图中所占的圆心角是 度.
(3)补全频数分布折线统计图.
(4)估计该校喜欢排球的学生有多少人?
5、某校想了解学生每周的课外阅读时间情况,随机抽取了部分学生进行调查,对学生每周的课外阅读时间(单位:小时)进行分组整理,并绘制了如图所示的不完整的频数分布直方图和扇形统计图:
( http: / / www.21cnjy.com / )
根据以上信息,解答下列问题:
(1)本次调查共随机抽取了_____________名学生,并补全频数分布直方图;
(2)求扇形统计图中m的值和E组对应的圆心角度数;
(3)在该校3000名学生中,每周的课外阅读时间不小于6小时的学生约有________________名.
-参考答案-
一、单选题
1、B
【分析】
根据题意可得:共40个数据,知道一、二、三、五组的数据个数,用总数减去这几组频数,即可得到答案.
【详解】
解:由题意得:第四组的频数=40-(2+7+11+12)=8;
故选B.
【点睛】
本题是对频数的考查,掌握各小组频数之和等于数据总和是解题的关键.
2、C
【分析】
先求出反面朝上的频数,然后根据频率=频数÷总数求解即可
【详解】
解:∵小明抛一枚硬币100次,其中有60次正面朝上,
∴小明抛一枚硬币100次,其中有40次反面朝上,
∴反面朝上的频率=40÷100=0.4,
故选C.
【点睛】
本题主要考查了根据频数求频率,解题的关键在于能够熟练掌握频率=频数÷总数.
3、D
【分析】
首先比较平均数,平均数相同时选择方差较小的运动员参加.
【详解】
解:∵,
∴从丙和丁中选择一人参加比赛,
∵S丙2>S丁2,
∴选择丁参赛,
故选:D.
【点睛】
此题考查了平均数和方差,正确理解方差与平均数的意义是解题关键.
4、B
【分析】
极差除以组距,大于或等于该值的最小整数即为组数.
【详解】
解:,
分10组.
故选:B.
【点睛】
本题考查了组距的划分,一般分为组最科学.
5、D
【分析】
由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似,根据以上逐项分析可知.21·世纪*教育网
【详解】
解:A. 旅客上飞机前的安检,人员不多,且这个调查很重要不可漏掉任何人,适合全面调查,不符合题意, 【出处:21教育名师】
B. 企业招聘,对应试人员进行面试,人员不多,且这个调查很重要不可漏掉任何人,适合全面调查,不符合题意,21教育名师原创作品
C. 了解全班同学每周体育锻炼的时间,人员不多,适合全面调查,不符合题意,
D. 调查市场上某种食品的色素含量是否符合国家标准,调查具有破坏性,不适合全面调查,符合题意
故选D
【点睛】
本题考查的是全面调查与抽样调查,在调查实际生 ( http: / / www.21cnjy.com )活中的相关问题时,要灵活处理,既要考虑问题本身的需要,又要考虑实现的可能性和所付出代价的大小.理解全面调查与抽样调查的适用范围是解题的关键.21·cn·jy·com
6、D
【分析】
根据抽样调查和全面调查的定义逐一判断即可.
【详解】
解|:A、调查甘肃人民春节期间的出行方式,应采用抽样调查,故不符合题意;
B、调查市场上纯净水的质量,应采用抽样调查,故不符合题意;
C、调查我市中小学生垃圾分类的意识,应采用抽样调查,故不符合题意;
D、调查某航班上的乘客是否都持有“绿色健康码”,应采用全面调查,故符合题意;
故选D.
【点睛】
本题考查了抽样调查和全面调查 ( http: / / www.21cnjy.com )的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
7、B
【分析】
由中位数的概念,即最中间一个或两个数据 ( http: / / www.21cnjy.com )的平均数;可知16人成绩的中位数是第8名和第9名的成绩.根据题意可得:参赛选手要想知道自己是否能进入前8名,只需要了解自己的成绩以及全部成绩的中位数,比较即可.
【详解】
解:由于16个人中,第8和第9名的成绩的平 ( http: / / www.21cnjy.com )均数是中位数,故同学知道了自己的分数后,想知道自己能否进入决赛,还需知道这16位同学的成绩的中位数.
故选:B.
【点睛】
此题主要考查统计的有关知识,主要包括 ( http: / / www.21cnjy.com )平均数、中位数、众数的意义.反映数据集中程度的统计量有平均数、中位数、众数等,各有局限性,因此要对统计量进行合理的选择和恰当的运用.
8、A
【分析】
根据抽样调查和普查的定义进行求解即可.
【详解】
解:A.调查一批防疫口罩的质量,适合抽样调查,故选项符合题意;
B.调查某校九年级学生的视力,适合全面调查,故选项不符合题意;
C.对乘坐某班次飞机的乘客进行安检,适合全面调查,故选项不符合题意;
D.国务院于2020年11月1日开展的第七次全国人口调查,适合全面调查,故选项不符合题意;
故选A.
【点睛】
本题考查了抽样调查和全面调查 ( http: / / www.21cnjy.com )的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.www.21-cn-jy.com
9、D
【分析】
根据频数之和等于总数,频数定义,加权平均数的计算,众数的定义逐项判断即可求解.
【详解】
解:A. 九年级(1)班共有学生10+20+15+5=50名,故原选项判断错误,不合题意;
B. 锻炼时间为8小时的学生有20名,故原选项判断错误,不合题意;
C. 平均数是小时,故原选项判断错误,不合题意;
D. 众数是8小时,故原选项判断正确,符合题意.
故选:D
【点睛】
本题考查了频数、加权平均数、众数等知识,理解相关概念,看到条形图是解题关键.
10、A
【分析】
根据方差的意义求解即可.
【详解】
解:∵S甲2=5,S乙2=20,S丙2=23,S丁2=32,
∴S甲2<S乙2<S丙2<S丁2,
∴这四名学生的数学成绩最稳定的是甲,
故选:A.
【点睛】
本题主要考查了方差,方差是反映一组数据的波 ( http: / / www.21cnjy.com )动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越差;反之,则它与其平均值的离散程度越小,稳定性越好.【版权所有:21教育】
二、填空题
1、16.5,17
【分析】
根据众数和中位数的定义求解即可,中 ( http: / / www.21cnjy.com )位数:将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数.如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.众数:在一组数据中出现次数最多的数.
【详解】
将,,,,,,,从小到大排列为:,,,,,,,
其中出现的次数最多,则众数为,
中位数为:.
故答案为:;
【点睛】
本题考查了求众数和中位数,理解众数和中位数的定义是解题的关键.
2、10
【分析】
求出每天的最高气温与最低气温的差,再比较大小即可.
【详解】
解:∵由折线统计图可知,
15日温差=4 ( 3)=7;
16日温差=4 ( 6)=10;
17日温差=2 ( 6)=8;
18日温差=2 ( 2)=4;
19日温差=1 ( 5)=6;
20日温差=1 ( 1)=2;
∴最大的温差是10.
故答案为:10.
【点睛】
本题考查了折线统计图的应用以及有理数的减法,掌握有理数减法法则是解答本题的关键.有理数减法法则:减去一个数,等于加上这个数的相反数.www-2-1-cnjy-com
3、甲班
【分析】
根据平均数相同,方差反应一组数据与平均数的离散程度越小说明比较稳定即可得出结论.
【详解】
解:∵两班的平均成绩相同,,根据方差反应一组数据与平均数的离散程度越小说明比较稳定,
∴成绩较为稳定的班级是甲班,
故答案为甲班.
【点睛】
本题考查平均数与方差,掌握平均数的求法与 ( http: / / www.21cnjy.com )方差的求法,熟练方差反应一组数据与平均数的离散程度,方差越大离散的程度越大,方差越小离散程度越小,越稳定,与整齐等是解题关键.
4、变大
【分析】
先由平均数的公式计算出李强第二次的平均数,再根据方差的公式进行计算,然后比较即可得出答案.
【详解】
解:∵李强再跳两次,成绩分别为7.6,8.0,
∴这组数据的平均数是,
∴这8次跳远成绩的方差是:
∵0.0225>,
∴方差变大;
故答案为:变大.
【点睛】
本题主要考查了平均数的计算和方差的计算,熟练掌握平均数和方差的计算是解答此题的关键.
5、86.5
【分析】
根据加权平均数的计算公式列出算式,再进行计算即可.
【详解】
解:根据题意得:
80×+85×+90×,
=16+25.5+45,
=86.5(分),
故答案为:86.5.
【点睛】
本题考查了加权平均数,解题的关键是掌握加权平均数的计算公式.
三、解答题
1、(1),,;(2)答案见解析.
【分析】
(1)分别根据平均数,方差,中位数的定义求解即可;
(2)从众数与中位数的角度分析,乙的射击成绩都比甲要高,从而可得结论.
【详解】
解:(1)由频数直方图可得:甲的成绩如下:
其中环出现了4次,所以众数是环,
环
由折线统计图可得:按从小到大排序为:
所以中位数为:.
故答案为:,,;
(2)从众数与中位数来看,乙的众数与中位数都比甲高,所以乙的射击成绩比甲的射击成绩要好一些.
【点睛】
本题考查的是平均数,众数,中位数,方差的含义,根据平均数,众数,中位数,方差下结论,掌握以上基础概念是解本题的关键.21*cnjy*com
2、(1)50人;(2)36°;(3)见解析
【分析】
(1)根据B的人数除以所占的百分比得到接受调查的学生人数;
(2)先求出D所占百分比,然后用360°×它所占百分比即可;
(3)先求出C所占百分比,再求出C的 ( http: / / www.21cnjy.com )人数,进而得出C中男生人数;用总人数乘A占的百分比得出A的人数进而得出A中女生人数,然后补全条形统计图即可;
【详解】
解:(1)根据题意得:(人)
答:本次接受调查的人数是50人;
(2)D占的百分比,
D所在的扇形圆心角的度数为;
(3)C占的百分比为1-(20%+40%+10%)=30%,
C的人数为50×30%=15(人),即C中男生为15-8=7(人);
A的人数为50×20%=10(人),A中女生人数为10-6=4(人),
补全条形统计图,如图所示:
( http: / / www.21cnjy.com / )
【点睛】
本题考查的是条形统计图和扇形统计图的综合 ( http: / / www.21cnjy.com )运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.21世纪教育网版权所有
3、
(1)4,12,80
(2)775人
(3)八年级的学生对党史知识掌握的总体水平较好(答案不唯一,合理即可).
【分析】
(1)根据所收集的收据即可确定a、b的值,中位数是指一组数据中位于中间位置的数,假设数据中的总数为N,若N为奇数,中位数为第个数据;若样本数为偶数,中位数为第个数据和第数据的平均值,据此可确定C;21cnjy.com
(2)先分别求出七、八年级80分以上学生所占的百分比,然后列式计算即可;
(3)根据平均数、众数和中位数进行分析即可.
(1)
解:由题意知八年级70≤x<80共4人,80≤x<90共12人,
∴a=4,b=12,
∵七年级80分共有4人,
∴七年级成绩的众数80,
∴c=80,
故答案为:4,12,80;
(2)
解:该校七年级学生在本次竞赛中成绩在80分以上所占的百分比为16÷20×100%=80%
该校八年级学生在本次竞赛中成绩在80分以上所占的百分比为15÷20×100%=75%
所以估计该校七、八两个年级学生在本次竞赛中成绩在80分以上的共有500×80%+500×75%=775(人).2-1-c-n-j-y
(3)
解:八年级的总体水平较好,理由如下:
∵七、八年级的平均成绩相等,而八年级的中位数为85,七年级的中位数为81.5
85>81.5,
∴八年级得分高的人数相对较多,
∴八年级的学生对党史知识掌握的总体水平较好(答案不唯一,合理即可).
【点睛】
本题主要考查了数据的统计、求中位数以及运用中位数进行决策、用样本估计总体等知识点,正确的统计是基础、灵活应用相关知识是解答本题的关键.
4、(1)100;(2)36;(3)见解析;(4)286
【分析】
(1)用乒乓球的人数除以其百分比即可得到调查的学生数;
(2)先计算出喜欢篮球的人数,得到喜欢排球的人数,根据公式计算喜欢排球的人数在扇形统计图中所占的圆心角度数;
(3)根据(2)的数据补全统计图;
(4)用学校的总人数乘以喜欢排球的比例即可得到答案.
【详解】
解:调查的学生有(名),
故答案为:100;
(2)喜欢篮球的人数有(名),
喜欢排球的人数是100-30-20-40=10(名),
∴喜欢排球的人数在扇形统计图中所占的圆心角是,
故答案为:36;
(3)如图:
( http: / / www.21cnjy.com / )
(4)该校喜欢排球的学生有(人).
【点睛】
本题考查的是条形统计图和扇形统 ( http: / / www.21cnjy.com )计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
5、
(1)100,图见解析
(2),
(3)
【分析】
(1)组人数组所占百分比被调查总人数,将总人数组所占百分比组人数;
(2)组人数调查总人数,组对应的圆心角度数组占调查人数比例;
(3)将样本中课外阅读时间不小于6小时的百分比乘以3000可得.
(1)
解:(1)随机调查学生数为:(人,
课外阅读时间在小时之间的人数为:(人,
补全图形如下:
( http: / / www.21cnjy.com / )
故答案是:100;
(2)
解:,
组对应的圆心角为:;
(3)
解:(人.
估计该校3000名学生每周的课外阅读时间不小于6小时的人数约为870人,
故答案是:.
【点睛】
本题考查的是条形统计图和 ( http: / / www.21cnjy.com )扇形统计图的综合运用,解题的关键是读懂统计图,从不同的统计图中得到必要的信息,条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
