沪教版(上海)九下 第二十八章统计初步综合测评试题(含详解)
文档属性
| 名称 | 沪教版(上海)九下 第二十八章统计初步综合测评试题(含详解) |  | |
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-23 16:25:27 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
九年级数学第二学期第二十八章统计初步综合测评
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题 ( http: / / www.21cnjy.com )目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。【出处:21教育名师】
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、已知小明在一次面试中的成绩为创新:87 ( http: / / www.21cnjy.com ),唱功:95,综合知识:89;若三项测试得分分别赋予权重3,6,1,则小明的平均成绩是( )【版权所有:21教育】
A.90 B.90.3 C.91 D.92
2、新冠疫情防控形势下,学校要求学生每日测量体温.某同学连续一周的体温情况如表所示,则该同学这一周的体温数据的众数和中位数分别是( )
日期 星期一 星期二 星期三 星期四 星期五 星期六 星期天
体温(℃) 36.3 36.7 36.2 36.3 36.2 36.4 36.3
A.36.3和36.2 B.36.2和36.3 C.36.3和36.3 D.36.2和36.1
3、下列做法正确的是( )
A.在嫦娥五号着陆器发射前,对其零件的检测采用抽样调查
B.本学期共进行了8次数学测试,小明想要清楚地知道自己成绩的走势,最好把8次成绩绘制成扇形统计图
C.为了调查宣城市七年级学生的体重情况,小刚对收集来的本校七年级同学体重数据进行了从大到小的排序,把排名前50的同学体重作为一个样本【来源:21cnj*y.co*m】
D.绘制扇形统计图时,要检查各部分所对应的圆心角之和是否等于360度
4、为了调查某校七年级学生的身高情况,在七年级的600名学生中随机抽取了50名学生,下列说法正确的是( )21·世纪*教育网
A.此次调查的总体是600名学生 B.此次调查属于全面调查
C.此次调查的个体是被抽取的学生 D.样本容量是50
5、下列调查中,最适合采用普查方式的是( )
A.调查一批电脑的使用寿命
B.调查某航班的乘客是否都持有“绿色健康码”
C.了解我市初中生的视力情况
D.调查河南卫视“中秋奇妙游”节目的收视率
6、下列调查中,最适合采用全面调查(普查)方式的是( )
A.检测生产的鞋底能承受的弯折次数
B.了解某批扫地机器人平均使用时长
C.选出短跑最快的学生参加全市比赛
D.了解某省初一学生周体育锻炼时长
7、小颖同学参加学校举办的“ ( http: / / www.21cnjy.com )抗击疫情,你我同行”主题演讲比赛,她的演讲内容、语言表达和形象风度三项得分分别为86分、90分、80分,若这三项依次按照50%,40%,10%的百分比确定成绩,则她的成绩为( )21世纪教育网版权所有
A.84分 B.85分 C.86分 D.87分
8、下列调查中,适合用普查方式的是( )
A.调查佛山市市民的吸烟情况
B.调查佛山市电视台某节目的收视率
C.调查佛山市市民家庭日常生活支出情况
D.调查佛山市某校某班学生对“文明佛山”的知晓率
9、在一次科技作品制作比 ( http: / / www.21cnjy.com )赛中,某小组八件作品的成绩(单位:分)分别是:7,10,9,8,7,9,9,8.对这组数据,下列说法正确的是( )21*cnjy*com
A.平均数是8 B.众数是8.5 C.中位数8.5 D.极差是5
10、甲、乙、丙、丁四名同学进行立定跳远测试,每人10次立定跳远成绩的平均数都是2.25米,方差分别是,,,,则这四名同学立定跳远成绩最稳定的是( ).
A.甲 B.乙 C.丙 D.丁
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、当今最常用的购物软件“手机淘 ( http: / / www.21cnjy.com )宝”的英语翻译为“mobile phone Taobao”,其中字母“o”出现的频率为__________.
2、某校七年级二班在订购本班的班 ( http: / / www.21cnjy.com )服前,按身高型号进行登记,对女生的记录中,身高150cm以下记为S号,150~160cm记为M号,160~170cm记为L号.170cm以上记为XL号.若绘制成统计图描述这些数据,合适的统计图是_____(填“条形”、“折线”、“扇形”中的一个)统计图.
3、甲、乙两名篮球运动员进行每组10次的投篮训练,5组投篮结束后,两人的平均命中数都是7次,方差分别是,,则在本次训练中,运动员__________的成绩更稳定.
4、一个扇形统计图中,某部分占总体的百分比为13%,则该部分所对扇形圆心角为______.
5、数据6,3,9,7,1的极差是_________.
三、解答题(5小题,每小题10分,共计50分)
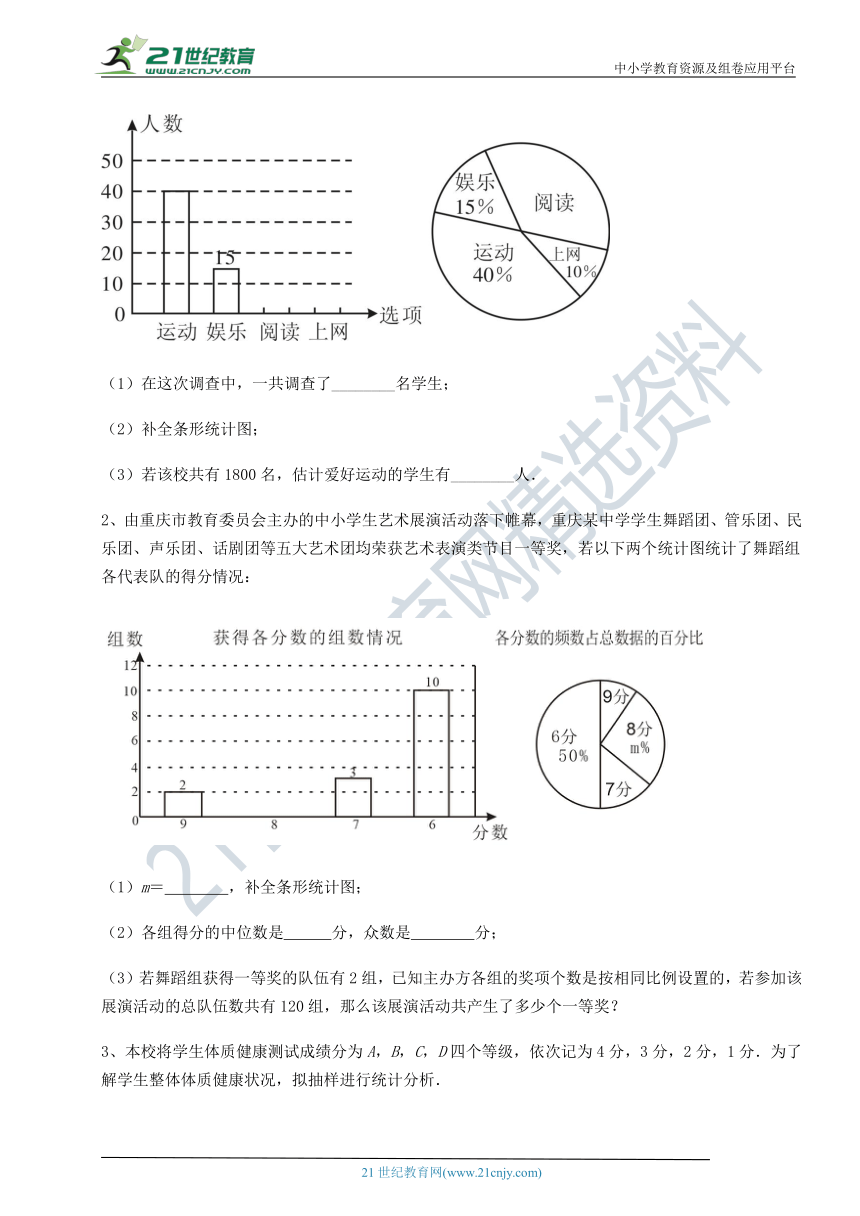
1、某校了解学生的课余爱好情 ( http: / / www.21cnjy.com )况,采取抽样调查的方法,从阅读、运动、娱乐、上网等四个方面调查了若干名学生的兴趣爱好,并将调查结果绘制成下面两幅不完整的统计图,请根据图中提供的信息解答下列问题:2·1·c·n·j·y
( http: / / www.21cnjy.com / )
(1)在这次调查中,一共调查了________名学生;
(2)补全条形统计图;
(3)若该校共有1800名,估计爱好运动的学生有________人.
2、由重庆市教育委员会主办的 ( http: / / www.21cnjy.com )中小学生艺术展演活动落下帷幕,重庆某中学学生舞蹈团、管乐团、民乐团、声乐团、话剧团等五大艺术团均荣获艺术表演类节目一等奖,若以下两个统计图统计了舞蹈组各代表队的得分情况:
( http: / / www.21cnjy.com / )
(1)m= ,补全条形统计图;
(2)各组得分的中位数是 分,众数是 分;
(3)若舞蹈组获得一等奖的队伍有2 ( http: / / www.21cnjy.com )组,已知主办方各组的奖项个数是按相同比例设置的,若参加该展演活动的总队伍数共有120组,那么该展演活动共产生了多少个一等奖?
3、本校将学生体质健康测试成绩分为A,B,C,D四个等级,依次记为4分,3分,2分,1分.为了解学生整体体质健康状况,拟抽样进行统计分析.
(1)现将随机抽取的测试成绩整理并绘制成如图统计图,请求出这组数据的平均数、中位数和众数;
本校部分学生体质健康测试成绩统计图
( http: / / www.21cnjy.com / )
(2)本校规定达到3分才算合格. 已知本校共有学生1600人,根据以上数据估计本校学生体质健康测试成绩达到合格的人数;
(3)为了更好贯彻落实健康第一的指导思想,请你根据以上数据对本校体育老师提出一条合理的建议.
4、某校随机抽取部分学生,对“学习 ( http: / / www.21cnjy.com )习惯”进行问卷调查.设计的问题:对自己做错的题目进行整理、分析、改正;答案选项为:A.很少;B.有时;C.常常;D.总是.将调查结果的数据进行了整理、绘制成如图两幅不完整的统计图.
( http: / / www.21cnjy.com / )
请根据图中信息,解答下列问题:
(1)填空:a= %,b= %;
(2)请你补全条形统计图;
(3)若该校有2000名学生,请你估计其中“常常”和“总是”对错题进行整理、分析、改正的学生各有多少名?21*cnjy*com
5、某校组织1002名学生参加“展示我美丽祖国”庆国庆的自拍照片的评比活动.随机抽取一些学生在评比中的成绩制成的统计图表如表:
频数分布表
分数段 频数 百分比
80≤x<85 a 20%
85≤x<90 80 b
90≤x<95 60 30%
95≤x<100 20
根据以上图表提供的信息,解答下列问题:
(1)写出表中a、b的数值:a= ,b= ;
(2)补全频数分布表和频数分布直方图;
( http: / / www.21cnjy.com / )
(3)如果评比成绩在95分以上的可以获得一等奖,试估计该校参加此次活动获得一等奖的人数.
-参考答案-
一、单选题
1、D
【分析】
根据加权平均数计算.
【详解】
解:小明的平均成绩为分,
故选:D.
【点睛】
此题考查了加权平均数,正确掌握各权重的意义及计算公式是解题的关键.
2、C
【分析】
根据中位数、众数的意义求解即可.
【详解】
解:把已知数据按照由小到大的顺序重新排序后为36.2,36.2,36.3,36.3,36.3,36.4,36.7,
该名同学这一周体温出现次数最多的是36.3℃,共出现3次,因此众数是36.3,
将这七天的体温从小到大排列处在中间位置的一个数是36.3℃,因此中位数是36.3,
故选:C.
【点睛】
本题考查中位数、众数,理解中位数、众数的意义是解题的关键.
3、D
【分析】
根据抽样调查与全面调查的概念、扇形统计图、条形统计图、折线统计图的优势,抽样调查中样本的代表性逐一判断即可.
【详解】
解:A.在嫦娥五号着陆器发射前,对其零件的检测采用全面调查,故此选项错误,不合题意;
B.本学期共进行了8次数学测试,小明想要清楚地知道自己成绩的走势,最好把8次成绩绘制成折线统计图,故此选项错误,不合题意;
C.为了调查宣城市七年级学生的体重情况,小刚 ( http: / / www.21cnjy.com )对收集来的本校七年级同学体重数据进行了从大到小的排序,把排名前50的同学体重作为一个样本不具有代表性,故此选项错误,不合题意;
D.绘制扇形统计图时,要检查各部分所对应的圆心角之和是否等于360度,此选项正确,符合题意.
故选:D
【点睛】
本题考查了抽样调查与全面调查的特点,统计图的特点,抽样调查样本的选择等情况,熟知相关知识并根据题意灵活应用是解题关键.www.21-cn-jy.com
4、D
【分析】
总体是指考查的对象的全体,个体是总体中的 ( http: / / www.21cnjy.com )每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目,我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考查的对象,从而找出总体、个体.再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量.
【详解】
解:A、此次调查的总体是某校七年级学生的身高情况,故本选项不合题意;
B、此次调查属于抽样调查,故本选项不合题意;
C、此次调查的个体是每一名七年级学生的身高情况,故本选项不合题意;
D、样本容量是50.故本选项符合题意.
故选:D.
【点睛】
本题考查了数据的收集,解题要分清具体问题中的 ( http: / / www.21cnjy.com )总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小,样本容量是样本中包含的个体的数目,不能带单位.
5、B
【分析】
由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.
【详解】
解:A.调查一批电脑的使用寿命,适合采用抽样调查的方式,故本选项不合题意;
B.调查某航班的乘客是否都持有“绿色健康码”,适合采用普查的方式,故本选项符合题意;
C.了解我市初中生的视力情况,适合采用抽样调查的方式,故本选项不合题意;
D.调查央视“五一晚会”的收视率,适合采用抽样调查的方式,故本选项不合题意.
故选:B.
【点睛】
本题考查了抽样调查和全面调查的区别,选择普查 ( http: / / www.21cnjy.com )还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.www-2-1-cnjy-com
6、C
【分析】
根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似解答.
【详解】
解:A、检测生产的鞋底能承受的弯折次数,具有破坏性,适合采用抽样调查;
B、了解某批扫地机器人平均使用时长,具有破坏性,适合采用抽样调查;
C、选出短跑最快的学生参加全市比赛,精确度要求高,适合采用全面调查;
D、了解某省初一学生周体育锻炼时长,调查数量较大且调查结果要求准确度不高,适合采用抽样调查;
故选:C.
【点睛】
本题考查的是抽样调查和全面调查, ( http: / / www.21cnjy.com )选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
7、D
【分析】
根据加权平均数的计算公式列出算式,再进行计算即可得出答案.
【详解】
解:根据题意得:
86×50%+90×40%+80×10%
=43+36+8
=87(分).
故选:D.
【点睛】
本题考查的是加权平均数的求法,本题易出现的错误是求86,90,80这三个数的算术平均数,对平均数的理解不正确.21·cn·jy·com
8、D
【分析】
根据普查和抽样调查的定义进行逐一判断即可.
【详解】
解:A、调查佛山市市民的吸烟情况,应采用抽样调查,故此选项不符合题意;
B、调查佛山市电视台某节目的收视率,应采用抽样调查,故此选项不符合题意;
C、调查佛山市市民家庭日常生活支出情况,应采用抽样调查,故此选项不符合题意;
D、调查佛山市某校某班学生对“文明佛山”的知晓率,应采用普查,故此选项符合题意;
故选D.
【点睛】
本题考查了抽样调查和全面调查 ( http: / / www.21cnjy.com )的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
9、C
【分析】
计算这组数据的平均数、众数、中位数及极差即可作出判断.
【详解】
这组数据的平均数为:,众数为9,中位数为8.5,极差为10-7=3,故正确的是中位数为8.5.
故选:C
【点睛】
本题考查了反映一组数据平均数、众数、中位数、极差等知识,正确计算这些统计量是关键.
10、D
【分析】
平均数相同,方差值越小越稳定,比较四名同学方差值的大小即可.
【详解】
解:∵
∴丁同学的成绩最稳定
故选D.
【点睛】
本题考查了方差.解题的关键在于理解方差值越小的数据越稳定.
二、填空题
1、
【分析】
用字母“o”出现的个数除以总的字母个数即可得出答案.
【详解】
解:∵字母“o”出现的次数为4,
∴该英语中字母“o”出现的频率为;
故答案为:.
【点睛】
此题主要考查了频率,关键是掌握频率的定义,频率=频数÷数据总数.
2、条形
【分析】
条形统计图能很容易看出数量 ( http: / / www.21cnjy.com )的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可.21cnjy.com
【详解】
解:为了清晰显示四种型号衣服的具体数量,应选用条形统计图,
故答案为:条形.
【点睛】
此题主要考查统计图的选择,应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答.
3、乙
【分析】
先根据乙的方差比甲的方差小,再根据方差越大,波动就越大,数据越不稳定,方差越小,波动越小,数据越稳定即可得出答案.2-1-c-n-j-y
【详解】
解:∵,,
∴,
∴乙运动员的成绩更稳定;
故答案为:乙.
【点睛】
本题考查方差的意义.方差是用来衡 ( http: / / www.21cnjy.com )量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
4、46.8°
【分析】
利用占总体的百分比是,则这部分的圆心角是360度的,即可求出结果.
【详解】
解:该部分所对扇形圆心角为:.
故答案为:.
【点睛】
本题考查扇形统计图中扇形所对圆心角的度数与百分比的关系,熟练掌握扇形所对圆心角的计算方法是解题关键.
5、8
【分析】
根据极差的定义,分析即可,极差:一组数据中最大值与最小值的差叫做这组数据的极差.
【详解】
解:数据6,3,9,7,1的极差是
故答案为:
【点睛】
本题考查了极差定义,理解极差的定义是解题的关键.
三、解答题
1、(1)100;(2)见解析;(3)720
【分析】
(1)根据爱好娱乐人数的百分比,以及娱乐人数即可求出共调查的人数;
(2)根据两幅统计图即可求出阅读的人数、运动人数、以及上网的人数,从而可补全图形.
(3)利用样本估计总体即可估计爱好运动的学生人数.
【详解】
解:(1)爱好娱乐的人数为15,所占百分比为15%,
∴共调查人数为:15÷15%=100.
故填:100.
(2)爱好上网人数为:100×10%=10,
爱好运动人数为:100×40%=40,
爱好阅读人数为:100-15-10-40=35,
补全条形统计图,如图所示:
( http: / / www.21cnjy.com / )
(3)爱好运动的学生人数所占的百分比为40%,
则:该校共有学生大约有:1800×40%=720人;
所以,若该校共有1800名,估计爱好运动的学生有720人.
【点睛】
本题考查条形统计图、扇形统计图、用样本估计总体,解答本题的关键是明确题意,会从图标中获取有用信息.
2、(1)25,图见详解;(2)6.5;6;(3)12
【分析】
(1)根据条形统计图和扇形统计图中的数据,即可得到总的组数,进而得出各分数对应的组数,然后根据题意画出统计图;21教育名师原创作品
(2)根据中位数以及众数的定义进行判断,即可得到中位数以及众数的值;
(3)依据舞蹈组获得一等奖的队伍的比例,即可估计该展演活动共产生一等奖的组数.
【详解】
解:(1)(组),(组),
,
统计图如下:
( http: / / www.21cnjy.com / )
(2)∵8分这一组的组数为5,
∴各组得分的中位数是,
分数为6分的组数最多,故众数为6;
故答案为:6.5,6;
(3)由题可得,(组,
该展演活动共产生了12个一等奖.
【点睛】
本题主要考查了条形统计图以及扇形 ( http: / / www.21cnjy.com )统计图的应用,通过扇形统计图可以很清楚地表示出各部分数量同总数之间的关系,从条形图可以很容易看出数据的大小,便于比较.
3、(1)平均数是2.75分、中位数是3分,众数是3分;(2)1000人;(3)(加强体育锻炼)答案不唯一.
【分析】
(1)根据平均数,众数及中位数的求法依次计算即可;
(2)利用总人数乘以合格人数占抽查总人数的比例即可;
(3)抓住健康第一,建议合理即可.
【详解】
解:(1)平均数为:;
抽查的120人中,成绩是3分出现的次数最多,共出现45次,因此众数是3分;
将这120人的得分从小到大排列处在60,61两个位置的分数都是3分,因此中位数是3分;
答:这组数据的平均数是2.75分,中位数是3分,众数是3分;
(2)估计本校学生体质健康测试成绩达到合格的人数为:
(人),
∴估计本校学生体质健康测试成绩达到合格的人数为1000人;
(3)加强体育锻炼(答案不唯一,合理即可).
【点睛】
题目主要考查从条形统计图获取信息,计算平均数,中位数,众数及利用部分估计整体,熟练掌握各个数据的计算方法是解题关键.【来源:21·世纪·教育·网】
4、(1)12,36;(2)见解析;(3)720人
【分析】
(1)首先计算出抽查的学生总数,然后再计算a、b的值即可;
(2)计算出“常常”所对的人数,然后补全统计图即可;
(3)利用样本估计总体的方法计算即可.
【详解】
解:(1)调查总人数:(人),
,
,
故答案为:12,36;
(2)“常常”所对的人数:200×30%=60(人),
补全统计图如图所示:
( http: / / www.21cnjy.com / );
(3)2000×30%=600(人),
2000×36%=720(人),
答:“常常”对错题进行整理、分析、改正的有600人,“总是”对错题进行整理、分析、改正的有720人.
【点睛】
本题考查条形统计图与扇形统 ( http: / / www.21cnjy.com )计图的综合运用,熟练掌握抽样的各项数目、各项百分比、总数、各项圆心角及整体的各项数目、各项百分比、总数等的计算方法是解题关键.
5、
(1)40,40%
(2)见解析
(3)100人
【分析】
(1)首先求得抽取的样本总数,然后用样本容量减去其他小组的人数即可求得a值,用80除以样本容量即可求得b值;
(2)根据上题求得的数据补全统计图即可;
(3)用总人数乘以获得一等奖的百分率即可求得获得一等奖的人数.
【小题1】
解:∵抽查的学生总数为:60÷30%=200(人),
∴a=200-80-60-20=40;b=×100%=40%.
【小题2】
成绩在95≤x<100的学生人数所占百分比为:×100%=10%,
故频数分布表为:
分数段 频数 百分比
80≤x<85 40 20%
85≤x<90 80 40%
90≤x<95 60 30%
95≤x<100 20 10%
频数分布直方图为:
( http: / / www.21cnjy.com / )【小题3】
1000×10%=100(人),
答:该校参加此次活动获得一等奖的人数是100人.
【点睛】
本题考查了频数分布直方图、频数分布表的 ( http: / / www.21cnjy.com )有关知识,读图时要全面细致,要充分运用数形结合思想来解决由统计图形式给出的数学实际问题.掌握好频率、中位数的概念.21教育网
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
九年级数学第二学期第二十八章统计初步综合测评
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题 ( http: / / www.21cnjy.com )目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。【出处:21教育名师】
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、已知小明在一次面试中的成绩为创新:87 ( http: / / www.21cnjy.com ),唱功:95,综合知识:89;若三项测试得分分别赋予权重3,6,1,则小明的平均成绩是( )【版权所有:21教育】
A.90 B.90.3 C.91 D.92
2、新冠疫情防控形势下,学校要求学生每日测量体温.某同学连续一周的体温情况如表所示,则该同学这一周的体温数据的众数和中位数分别是( )
日期 星期一 星期二 星期三 星期四 星期五 星期六 星期天
体温(℃) 36.3 36.7 36.2 36.3 36.2 36.4 36.3
A.36.3和36.2 B.36.2和36.3 C.36.3和36.3 D.36.2和36.1
3、下列做法正确的是( )
A.在嫦娥五号着陆器发射前,对其零件的检测采用抽样调查
B.本学期共进行了8次数学测试,小明想要清楚地知道自己成绩的走势,最好把8次成绩绘制成扇形统计图
C.为了调查宣城市七年级学生的体重情况,小刚对收集来的本校七年级同学体重数据进行了从大到小的排序,把排名前50的同学体重作为一个样本【来源:21cnj*y.co*m】
D.绘制扇形统计图时,要检查各部分所对应的圆心角之和是否等于360度
4、为了调查某校七年级学生的身高情况,在七年级的600名学生中随机抽取了50名学生,下列说法正确的是( )21·世纪*教育网
A.此次调查的总体是600名学生 B.此次调查属于全面调查
C.此次调查的个体是被抽取的学生 D.样本容量是50
5、下列调查中,最适合采用普查方式的是( )
A.调查一批电脑的使用寿命
B.调查某航班的乘客是否都持有“绿色健康码”
C.了解我市初中生的视力情况
D.调查河南卫视“中秋奇妙游”节目的收视率
6、下列调查中,最适合采用全面调查(普查)方式的是( )
A.检测生产的鞋底能承受的弯折次数
B.了解某批扫地机器人平均使用时长
C.选出短跑最快的学生参加全市比赛
D.了解某省初一学生周体育锻炼时长
7、小颖同学参加学校举办的“ ( http: / / www.21cnjy.com )抗击疫情,你我同行”主题演讲比赛,她的演讲内容、语言表达和形象风度三项得分分别为86分、90分、80分,若这三项依次按照50%,40%,10%的百分比确定成绩,则她的成绩为( )21世纪教育网版权所有
A.84分 B.85分 C.86分 D.87分
8、下列调查中,适合用普查方式的是( )
A.调查佛山市市民的吸烟情况
B.调查佛山市电视台某节目的收视率
C.调查佛山市市民家庭日常生活支出情况
D.调查佛山市某校某班学生对“文明佛山”的知晓率
9、在一次科技作品制作比 ( http: / / www.21cnjy.com )赛中,某小组八件作品的成绩(单位:分)分别是:7,10,9,8,7,9,9,8.对这组数据,下列说法正确的是( )21*cnjy*com
A.平均数是8 B.众数是8.5 C.中位数8.5 D.极差是5
10、甲、乙、丙、丁四名同学进行立定跳远测试,每人10次立定跳远成绩的平均数都是2.25米,方差分别是,,,,则这四名同学立定跳远成绩最稳定的是( ).
A.甲 B.乙 C.丙 D.丁
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、当今最常用的购物软件“手机淘 ( http: / / www.21cnjy.com )宝”的英语翻译为“mobile phone Taobao”,其中字母“o”出现的频率为__________.
2、某校七年级二班在订购本班的班 ( http: / / www.21cnjy.com )服前,按身高型号进行登记,对女生的记录中,身高150cm以下记为S号,150~160cm记为M号,160~170cm记为L号.170cm以上记为XL号.若绘制成统计图描述这些数据,合适的统计图是_____(填“条形”、“折线”、“扇形”中的一个)统计图.
3、甲、乙两名篮球运动员进行每组10次的投篮训练,5组投篮结束后,两人的平均命中数都是7次,方差分别是,,则在本次训练中,运动员__________的成绩更稳定.
4、一个扇形统计图中,某部分占总体的百分比为13%,则该部分所对扇形圆心角为______.
5、数据6,3,9,7,1的极差是_________.
三、解答题(5小题,每小题10分,共计50分)
1、某校了解学生的课余爱好情 ( http: / / www.21cnjy.com )况,采取抽样调查的方法,从阅读、运动、娱乐、上网等四个方面调查了若干名学生的兴趣爱好,并将调查结果绘制成下面两幅不完整的统计图,请根据图中提供的信息解答下列问题:2·1·c·n·j·y
( http: / / www.21cnjy.com / )
(1)在这次调查中,一共调查了________名学生;
(2)补全条形统计图;
(3)若该校共有1800名,估计爱好运动的学生有________人.
2、由重庆市教育委员会主办的 ( http: / / www.21cnjy.com )中小学生艺术展演活动落下帷幕,重庆某中学学生舞蹈团、管乐团、民乐团、声乐团、话剧团等五大艺术团均荣获艺术表演类节目一等奖,若以下两个统计图统计了舞蹈组各代表队的得分情况:
( http: / / www.21cnjy.com / )
(1)m= ,补全条形统计图;
(2)各组得分的中位数是 分,众数是 分;
(3)若舞蹈组获得一等奖的队伍有2 ( http: / / www.21cnjy.com )组,已知主办方各组的奖项个数是按相同比例设置的,若参加该展演活动的总队伍数共有120组,那么该展演活动共产生了多少个一等奖?
3、本校将学生体质健康测试成绩分为A,B,C,D四个等级,依次记为4分,3分,2分,1分.为了解学生整体体质健康状况,拟抽样进行统计分析.
(1)现将随机抽取的测试成绩整理并绘制成如图统计图,请求出这组数据的平均数、中位数和众数;
本校部分学生体质健康测试成绩统计图
( http: / / www.21cnjy.com / )
(2)本校规定达到3分才算合格. 已知本校共有学生1600人,根据以上数据估计本校学生体质健康测试成绩达到合格的人数;
(3)为了更好贯彻落实健康第一的指导思想,请你根据以上数据对本校体育老师提出一条合理的建议.
4、某校随机抽取部分学生,对“学习 ( http: / / www.21cnjy.com )习惯”进行问卷调查.设计的问题:对自己做错的题目进行整理、分析、改正;答案选项为:A.很少;B.有时;C.常常;D.总是.将调查结果的数据进行了整理、绘制成如图两幅不完整的统计图.
( http: / / www.21cnjy.com / )
请根据图中信息,解答下列问题:
(1)填空:a= %,b= %;
(2)请你补全条形统计图;
(3)若该校有2000名学生,请你估计其中“常常”和“总是”对错题进行整理、分析、改正的学生各有多少名?21*cnjy*com
5、某校组织1002名学生参加“展示我美丽祖国”庆国庆的自拍照片的评比活动.随机抽取一些学生在评比中的成绩制成的统计图表如表:
频数分布表
分数段 频数 百分比
80≤x<85 a 20%
85≤x<90 80 b
90≤x<95 60 30%
95≤x<100 20
根据以上图表提供的信息,解答下列问题:
(1)写出表中a、b的数值:a= ,b= ;
(2)补全频数分布表和频数分布直方图;
( http: / / www.21cnjy.com / )
(3)如果评比成绩在95分以上的可以获得一等奖,试估计该校参加此次活动获得一等奖的人数.
-参考答案-
一、单选题
1、D
【分析】
根据加权平均数计算.
【详解】
解:小明的平均成绩为分,
故选:D.
【点睛】
此题考查了加权平均数,正确掌握各权重的意义及计算公式是解题的关键.
2、C
【分析】
根据中位数、众数的意义求解即可.
【详解】
解:把已知数据按照由小到大的顺序重新排序后为36.2,36.2,36.3,36.3,36.3,36.4,36.7,
该名同学这一周体温出现次数最多的是36.3℃,共出现3次,因此众数是36.3,
将这七天的体温从小到大排列处在中间位置的一个数是36.3℃,因此中位数是36.3,
故选:C.
【点睛】
本题考查中位数、众数,理解中位数、众数的意义是解题的关键.
3、D
【分析】
根据抽样调查与全面调查的概念、扇形统计图、条形统计图、折线统计图的优势,抽样调查中样本的代表性逐一判断即可.
【详解】
解:A.在嫦娥五号着陆器发射前,对其零件的检测采用全面调查,故此选项错误,不合题意;
B.本学期共进行了8次数学测试,小明想要清楚地知道自己成绩的走势,最好把8次成绩绘制成折线统计图,故此选项错误,不合题意;
C.为了调查宣城市七年级学生的体重情况,小刚 ( http: / / www.21cnjy.com )对收集来的本校七年级同学体重数据进行了从大到小的排序,把排名前50的同学体重作为一个样本不具有代表性,故此选项错误,不合题意;
D.绘制扇形统计图时,要检查各部分所对应的圆心角之和是否等于360度,此选项正确,符合题意.
故选:D
【点睛】
本题考查了抽样调查与全面调查的特点,统计图的特点,抽样调查样本的选择等情况,熟知相关知识并根据题意灵活应用是解题关键.www.21-cn-jy.com
4、D
【分析】
总体是指考查的对象的全体,个体是总体中的 ( http: / / www.21cnjy.com )每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目,我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考查的对象,从而找出总体、个体.再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量.
【详解】
解:A、此次调查的总体是某校七年级学生的身高情况,故本选项不合题意;
B、此次调查属于抽样调查,故本选项不合题意;
C、此次调查的个体是每一名七年级学生的身高情况,故本选项不合题意;
D、样本容量是50.故本选项符合题意.
故选:D.
【点睛】
本题考查了数据的收集,解题要分清具体问题中的 ( http: / / www.21cnjy.com )总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小,样本容量是样本中包含的个体的数目,不能带单位.
5、B
【分析】
由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.
【详解】
解:A.调查一批电脑的使用寿命,适合采用抽样调查的方式,故本选项不合题意;
B.调查某航班的乘客是否都持有“绿色健康码”,适合采用普查的方式,故本选项符合题意;
C.了解我市初中生的视力情况,适合采用抽样调查的方式,故本选项不合题意;
D.调查央视“五一晚会”的收视率,适合采用抽样调查的方式,故本选项不合题意.
故选:B.
【点睛】
本题考查了抽样调查和全面调查的区别,选择普查 ( http: / / www.21cnjy.com )还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.www-2-1-cnjy-com
6、C
【分析】
根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似解答.
【详解】
解:A、检测生产的鞋底能承受的弯折次数,具有破坏性,适合采用抽样调查;
B、了解某批扫地机器人平均使用时长,具有破坏性,适合采用抽样调查;
C、选出短跑最快的学生参加全市比赛,精确度要求高,适合采用全面调查;
D、了解某省初一学生周体育锻炼时长,调查数量较大且调查结果要求准确度不高,适合采用抽样调查;
故选:C.
【点睛】
本题考查的是抽样调查和全面调查, ( http: / / www.21cnjy.com )选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
7、D
【分析】
根据加权平均数的计算公式列出算式,再进行计算即可得出答案.
【详解】
解:根据题意得:
86×50%+90×40%+80×10%
=43+36+8
=87(分).
故选:D.
【点睛】
本题考查的是加权平均数的求法,本题易出现的错误是求86,90,80这三个数的算术平均数,对平均数的理解不正确.21·cn·jy·com
8、D
【分析】
根据普查和抽样调查的定义进行逐一判断即可.
【详解】
解:A、调查佛山市市民的吸烟情况,应采用抽样调查,故此选项不符合题意;
B、调查佛山市电视台某节目的收视率,应采用抽样调查,故此选项不符合题意;
C、调查佛山市市民家庭日常生活支出情况,应采用抽样调查,故此选项不符合题意;
D、调查佛山市某校某班学生对“文明佛山”的知晓率,应采用普查,故此选项符合题意;
故选D.
【点睛】
本题考查了抽样调查和全面调查 ( http: / / www.21cnjy.com )的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
9、C
【分析】
计算这组数据的平均数、众数、中位数及极差即可作出判断.
【详解】
这组数据的平均数为:,众数为9,中位数为8.5,极差为10-7=3,故正确的是中位数为8.5.
故选:C
【点睛】
本题考查了反映一组数据平均数、众数、中位数、极差等知识,正确计算这些统计量是关键.
10、D
【分析】
平均数相同,方差值越小越稳定,比较四名同学方差值的大小即可.
【详解】
解:∵
∴丁同学的成绩最稳定
故选D.
【点睛】
本题考查了方差.解题的关键在于理解方差值越小的数据越稳定.
二、填空题
1、
【分析】
用字母“o”出现的个数除以总的字母个数即可得出答案.
【详解】
解:∵字母“o”出现的次数为4,
∴该英语中字母“o”出现的频率为;
故答案为:.
【点睛】
此题主要考查了频率,关键是掌握频率的定义,频率=频数÷数据总数.
2、条形
【分析】
条形统计图能很容易看出数量 ( http: / / www.21cnjy.com )的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可.21cnjy.com
【详解】
解:为了清晰显示四种型号衣服的具体数量,应选用条形统计图,
故答案为:条形.
【点睛】
此题主要考查统计图的选择,应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答.
3、乙
【分析】
先根据乙的方差比甲的方差小,再根据方差越大,波动就越大,数据越不稳定,方差越小,波动越小,数据越稳定即可得出答案.2-1-c-n-j-y
【详解】
解:∵,,
∴,
∴乙运动员的成绩更稳定;
故答案为:乙.
【点睛】
本题考查方差的意义.方差是用来衡 ( http: / / www.21cnjy.com )量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
4、46.8°
【分析】
利用占总体的百分比是,则这部分的圆心角是360度的,即可求出结果.
【详解】
解:该部分所对扇形圆心角为:.
故答案为:.
【点睛】
本题考查扇形统计图中扇形所对圆心角的度数与百分比的关系,熟练掌握扇形所对圆心角的计算方法是解题关键.
5、8
【分析】
根据极差的定义,分析即可,极差:一组数据中最大值与最小值的差叫做这组数据的极差.
【详解】
解:数据6,3,9,7,1的极差是
故答案为:
【点睛】
本题考查了极差定义,理解极差的定义是解题的关键.
三、解答题
1、(1)100;(2)见解析;(3)720
【分析】
(1)根据爱好娱乐人数的百分比,以及娱乐人数即可求出共调查的人数;
(2)根据两幅统计图即可求出阅读的人数、运动人数、以及上网的人数,从而可补全图形.
(3)利用样本估计总体即可估计爱好运动的学生人数.
【详解】
解:(1)爱好娱乐的人数为15,所占百分比为15%,
∴共调查人数为:15÷15%=100.
故填:100.
(2)爱好上网人数为:100×10%=10,
爱好运动人数为:100×40%=40,
爱好阅读人数为:100-15-10-40=35,
补全条形统计图,如图所示:
( http: / / www.21cnjy.com / )
(3)爱好运动的学生人数所占的百分比为40%,
则:该校共有学生大约有:1800×40%=720人;
所以,若该校共有1800名,估计爱好运动的学生有720人.
【点睛】
本题考查条形统计图、扇形统计图、用样本估计总体,解答本题的关键是明确题意,会从图标中获取有用信息.
2、(1)25,图见详解;(2)6.5;6;(3)12
【分析】
(1)根据条形统计图和扇形统计图中的数据,即可得到总的组数,进而得出各分数对应的组数,然后根据题意画出统计图;21教育名师原创作品
(2)根据中位数以及众数的定义进行判断,即可得到中位数以及众数的值;
(3)依据舞蹈组获得一等奖的队伍的比例,即可估计该展演活动共产生一等奖的组数.
【详解】
解:(1)(组),(组),
,
统计图如下:
( http: / / www.21cnjy.com / )
(2)∵8分这一组的组数为5,
∴各组得分的中位数是,
分数为6分的组数最多,故众数为6;
故答案为:6.5,6;
(3)由题可得,(组,
该展演活动共产生了12个一等奖.
【点睛】
本题主要考查了条形统计图以及扇形 ( http: / / www.21cnjy.com )统计图的应用,通过扇形统计图可以很清楚地表示出各部分数量同总数之间的关系,从条形图可以很容易看出数据的大小,便于比较.
3、(1)平均数是2.75分、中位数是3分,众数是3分;(2)1000人;(3)(加强体育锻炼)答案不唯一.
【分析】
(1)根据平均数,众数及中位数的求法依次计算即可;
(2)利用总人数乘以合格人数占抽查总人数的比例即可;
(3)抓住健康第一,建议合理即可.
【详解】
解:(1)平均数为:;
抽查的120人中,成绩是3分出现的次数最多,共出现45次,因此众数是3分;
将这120人的得分从小到大排列处在60,61两个位置的分数都是3分,因此中位数是3分;
答:这组数据的平均数是2.75分,中位数是3分,众数是3分;
(2)估计本校学生体质健康测试成绩达到合格的人数为:
(人),
∴估计本校学生体质健康测试成绩达到合格的人数为1000人;
(3)加强体育锻炼(答案不唯一,合理即可).
【点睛】
题目主要考查从条形统计图获取信息,计算平均数,中位数,众数及利用部分估计整体,熟练掌握各个数据的计算方法是解题关键.【来源:21·世纪·教育·网】
4、(1)12,36;(2)见解析;(3)720人
【分析】
(1)首先计算出抽查的学生总数,然后再计算a、b的值即可;
(2)计算出“常常”所对的人数,然后补全统计图即可;
(3)利用样本估计总体的方法计算即可.
【详解】
解:(1)调查总人数:(人),
,
,
故答案为:12,36;
(2)“常常”所对的人数:200×30%=60(人),
补全统计图如图所示:
( http: / / www.21cnjy.com / );
(3)2000×30%=600(人),
2000×36%=720(人),
答:“常常”对错题进行整理、分析、改正的有600人,“总是”对错题进行整理、分析、改正的有720人.
【点睛】
本题考查条形统计图与扇形统 ( http: / / www.21cnjy.com )计图的综合运用,熟练掌握抽样的各项数目、各项百分比、总数、各项圆心角及整体的各项数目、各项百分比、总数等的计算方法是解题关键.
5、
(1)40,40%
(2)见解析
(3)100人
【分析】
(1)首先求得抽取的样本总数,然后用样本容量减去其他小组的人数即可求得a值,用80除以样本容量即可求得b值;
(2)根据上题求得的数据补全统计图即可;
(3)用总人数乘以获得一等奖的百分率即可求得获得一等奖的人数.
【小题1】
解:∵抽查的学生总数为:60÷30%=200(人),
∴a=200-80-60-20=40;b=×100%=40%.
【小题2】
成绩在95≤x<100的学生人数所占百分比为:×100%=10%,
故频数分布表为:
分数段 频数 百分比
80≤x<85 40 20%
85≤x<90 80 40%
90≤x<95 60 30%
95≤x<100 20 10%
频数分布直方图为:
( http: / / www.21cnjy.com / )【小题3】
1000×10%=100(人),
答:该校参加此次活动获得一等奖的人数是100人.
【点睛】
本题考查了频数分布直方图、频数分布表的 ( http: / / www.21cnjy.com )有关知识,读图时要全面细致,要充分运用数形结合思想来解决由统计图形式给出的数学实际问题.掌握好频率、中位数的概念.21教育网
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
