第七单元三角形、平行四边形和梯形开学前复习巩固自检卷(单元测试)小学数学四年级下册苏教版(含答案)
文档属性
| 名称 | 第七单元三角形、平行四边形和梯形开学前复习巩固自检卷(单元测试)小学数学四年级下册苏教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 981.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-24 11:45:35 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第七单元三角形、平行四边形和梯形开学前复习巩固自检卷(单元测试)-小学数学四年级下册苏教版
一、选择题
1.如果三角形的两边分别是4厘米、8厘米,则第三条边不可能是( )。
A.6厘米 B.5厘米 C.4厘米 D.11厘米
2.亮亮想知道下面三角形ABC三个内角度数的和,下面拼法中正确的是( )。
A. B. C.
3.以下是几组小棒的长度,可以摆成三角形的是( )。
A.3cm、5cm、2cm B.7cm、8cm、1cm
C.10cm、5cm、8cm D.4cm、13cm、7cm
4.下面说法正确的有( )个。
①三角形具有稳定性。
②三角形越大,该三角形的内角和就越大。
③我画了一个三角形,其中最小的角是61°。
④用3根分别长1cm、2cm、3cm的小棒,一定可以拼成一个三角形。
A.1 B.2 C.3 D.4
5.如图,已知a∥b,所以图中有( )个梯形。
A.4个 B.3个 C.2个 D.1个
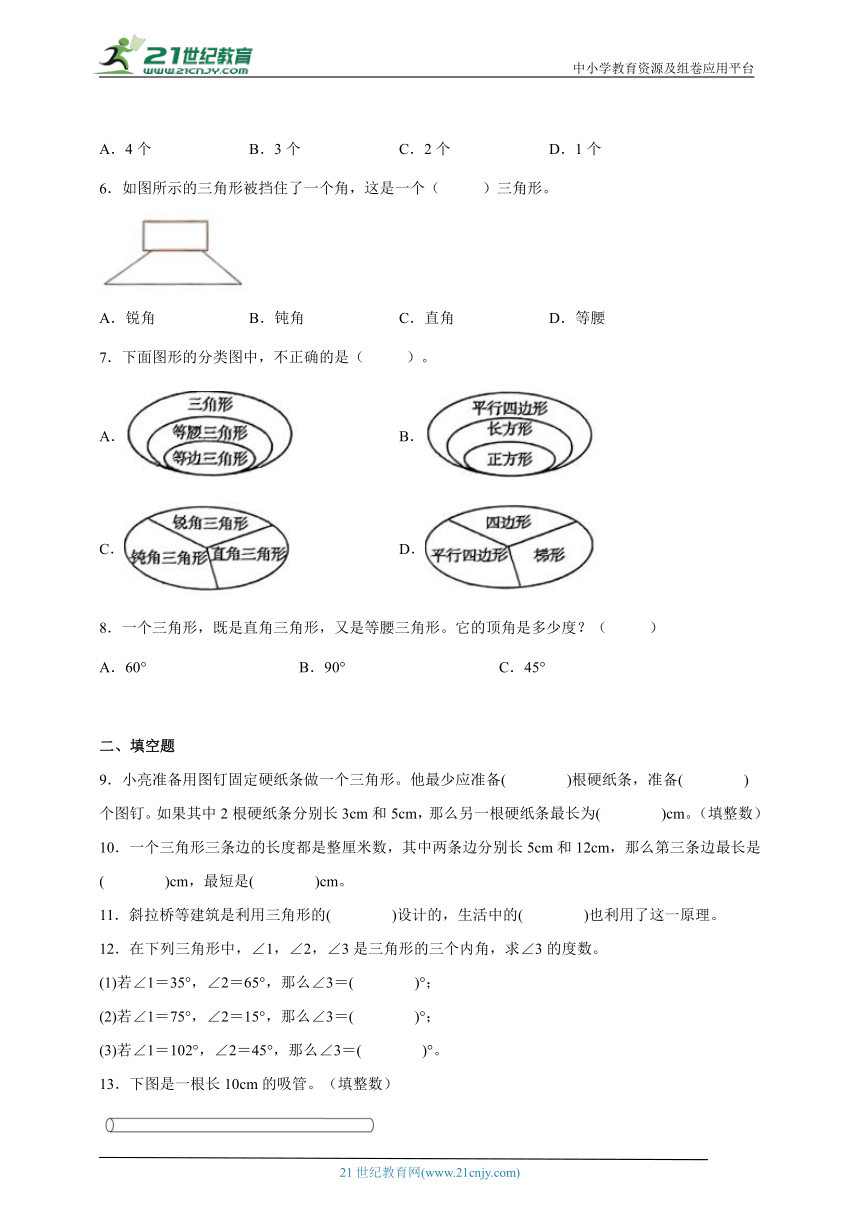
6.如图所示的三角形被挡住了一个角,这是一个( )三角形。
A.锐角 B.钝角 C.直角 D.等腰
7.下面图形的分类图中,不正确的是( )。
A. B.
C. D.
8.一个三角形,既是直角三角形,又是等腰三角形。它的顶角是多少度?( )
A.60° B.90° C.45°
二、填空题
9.小亮准备用图钉固定硬纸条做一个三角形。他最少应准备( )根硬纸条,准备( )个图钉。如果其中2根硬纸条分别长3cm和5cm,那么另一根硬纸条最长为( )cm。(填整数)
10.一个三角形三条边的长度都是整厘米数,其中两条边分别长5cm和12cm,那么第三条边最长是( )cm,最短是( )cm。
11.斜拉桥等建筑是利用三角形的( )设计的,生活中的( )也利用了这一原理。
12.在下列三角形中,∠1,∠2,∠3是三角形的三个内角,求∠3的度数。
(1)若∠1=35°,∠2=65°,那么∠3=( )°;
(2)若∠1=75°,∠2=15°,那么∠3=( )°;
(3)若∠1=102°,∠2=45°,那么∠3=( )°。
13.下图是一根长10cm的吸管。(填整数)
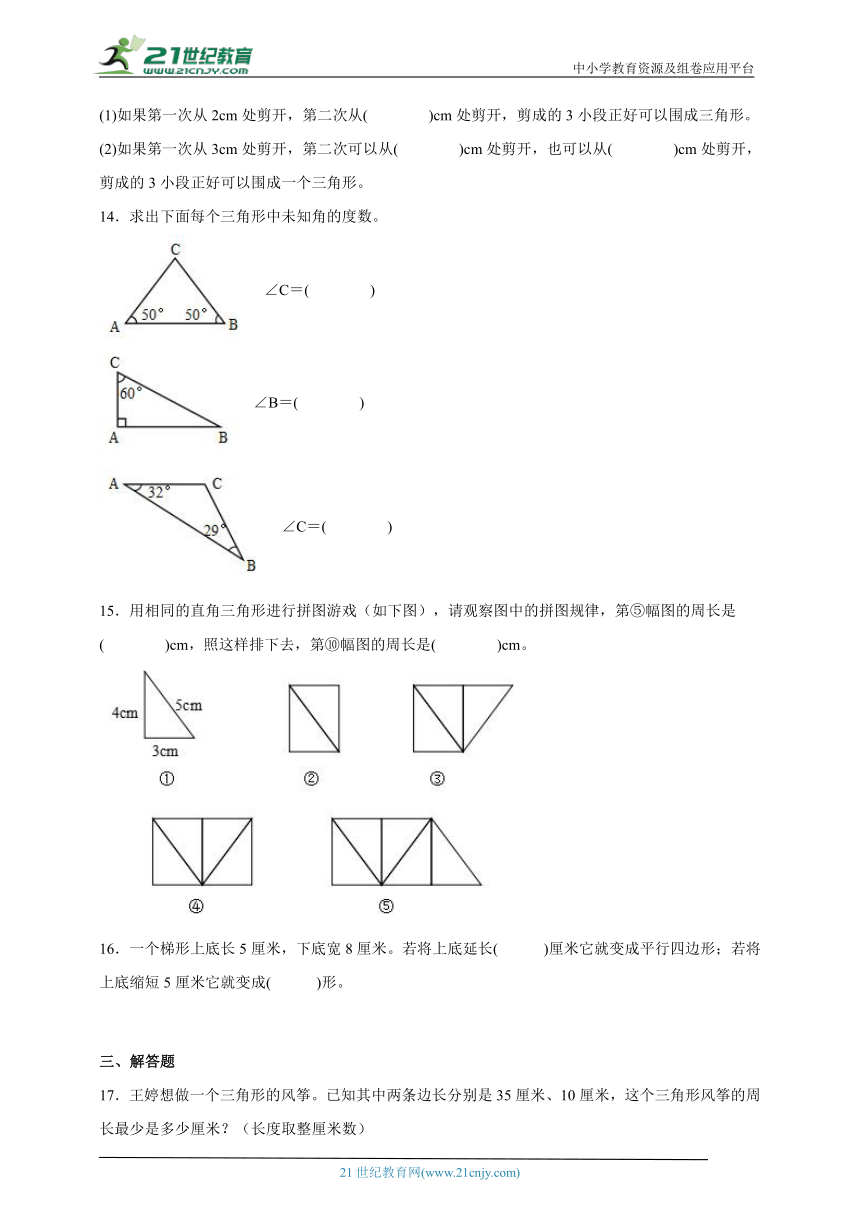
(1)如果第一次从2cm处剪开,第二次从( )cm处剪开,剪成的3小段正好可以围成三角形。
(2)如果第一次从3cm处剪开,第二次可以从( )cm处剪开,也可以从( )cm处剪开,剪成的3小段正好可以围成一个三角形。
14.求出下面每个三角形中未知角的度数。
∠C=( )
∠B=( )
∠C=( )
15.用相同的直角三角形进行拼图游戏(如下图),请观察图中的拼图规律,第⑤幅图的周长是( )cm,照这样排下去,第⑩幅图的周长是( )cm。
16.一个梯形上底长5厘米,下底宽8厘米。若将上底延长( )厘米它就变成平行四边形;若将上底缩短5厘米它就变成( )形。
三、解答题
17.王婷想做一个三角形的风筝。已知其中两条边长分别是35厘米、10厘米,这个三角形风筝的周长最少是多少厘米?(长度取整厘米数)
18.小刚想给他的小狗做一个房子,房顶的框架要做成三角形,其中一根木条长3分米,另一根长5分米,那么第三根木条的长度可能是多少分米?(长度取整分米数)
19.一个等腰三角形的周长是56厘米,腰比底长4厘米。它的底长和腰长各是多少厘米?(先画图,再解答)
20.赵大伯准备靠墙围一块梯形菜地,菜地的上底是18米,下底是32米,两条腰都是22米。已知墙的长度大于32米,则围这块菜地最少需要用篱笆多少米?(先画图,再解答)
21.一个等腰三角形的底角是顶角的2倍,这个等腰三角形的底角和顶角分别是多少?
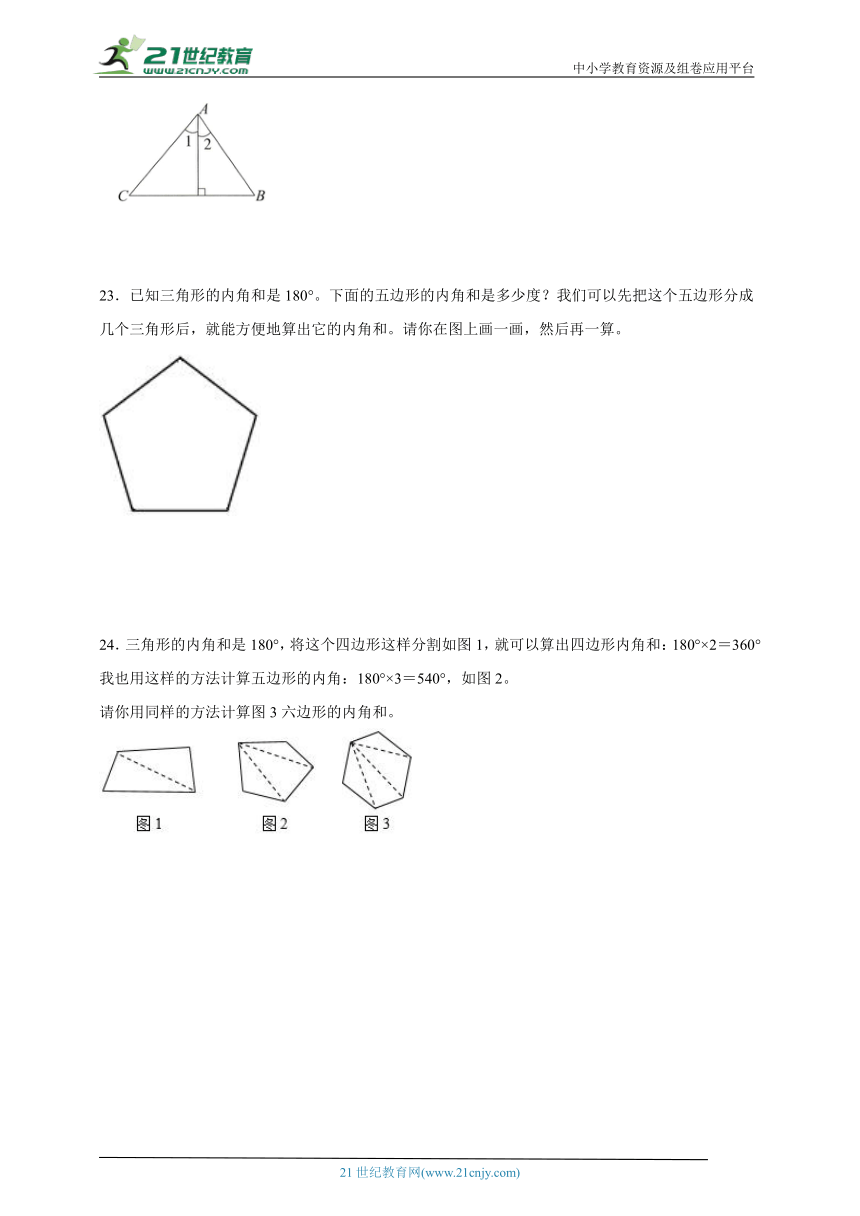
22.如图所示,已知∠1=40°,∠2=35°,求∠B和∠C的度数。
23.已知三角形的内角和是180°。下面的五边形的内角和是多少度?我们可以先把这个五边形分成几个三角形后,就能方便地算出它的内角和。请你在图上画一画,然后再一算。
24.三角形的内角和是180°,将这个四边形这样分割如图1,就可以算出四边形内角和:180°×2=360°
我也用这样的方法计算五边形的内角:180°×3=540°,如图2。
请你用同样的方法计算图3六边形的内角和。
参考答案:
1.C
【分析】根据三角形两边之和大于第三边,两边之差小于第三边,解答此题即可。
【详解】8-4=4(厘米)
8+4=12(厘米)
4厘米<第三边<12厘米
故答案为:C
【点睛】熟练掌握三角形的三边关系,是解答此题的关键。
2.C
【分析】要想知道三个内角度数的和,将三个内角组合成一个角才能利用量角器量出来,据此即可解答。
【详解】A.三个角中间有空隙,没有组成一个角,
B.三个角中间有空隙,没有组成一个角,
C.三个角中间没有空隙,组成一个角,可以测量,
故答案为:C
【点睛】本题考查了学生对内角和的认识和理解。
3.C
【分析】根据三角形的三边关系:两边之和大于第三边,三角形的两边的差一定小于第三边;进行依次分析即可。
【详解】A.3+2=5,不能围成三角形;
B.1+7=8,不能围成三角形;
C.5+8>10,能围成三角形;
D.4+7<13,不能围成三角形。
故答案为:C
【点睛】熟练掌握三角形的三边关系是解答此题的关键。
4.A
【分析】三角形具有稳定性;三角形的内角和是180°;三角形的三边关系:两边之和大于第三条边,两边之差小于第三条边。
【详解】①三角形具有稳定性,原题说法正确。
②任意三角形的内角和都是180°,原题说法错误。
③一个三角形,最小的角不一定就是61°,还可以更小的角,只要满足三角形的内角和是180°即可,原题说法错误。
④1+2=3,则长1cm、2cm、3cm的小棒,一定不可以拼成一个三角形;原题说法错误。
故答案为:A
【点睛】本题主要考查了学生对三角形具有稳定性、三角形的内角和定律、三角形的三边关系的掌握与理解。
5.B
【分析】梯形是只有一组对边平行的四边形,观察题图可知,四边形ADEB、四边形BEFC及四边形ADFC都是梯形,据此解答。
【详解】由分析得:图中一共有3个梯形。
故答案为:B
【点睛】本题考查梯形的特征,需熟练掌握。
6.B
【分析】先用量角器测量出已知的两个角的度数,再根据三角形的内角和,用180°依次减去已知两个角的度数,求出被挡住角的度数,进而判断这个三角形是什么三角形。
【详解】180°-35°-40°=105°
则被挡住的角是一个钝角,这个三角形是一个钝角三角形。
故答案为:B。
【点睛】本题关键是根据三角形的内角和求出被挡住角的度数。
7.D
【分析】三角形中,两条腰相等的三角形是等腰三角形,三条边相等的三角形是等腰三角形,则等边三角形是特殊的等腰三角形。平行四边形的两组对边平行,长方形的两组对边平行,4个角都是直角,正方形的两组对边平行,4个角都是直角,4条边相等,则正方形是特殊的长方形,长方形是特殊的平行四边形。锐角三角形不是特殊的钝角三角形,也不是特殊的直角三角形。平行四边形和梯形都是四边形,但是平行四边形不是特殊的梯形。
【详解】A.分类图正确;
B. 分类图正确;
C. 分类图正确;
D. 分类图不正确;
故答案为:D。
【点睛】本题考查三角形、四边形的分类,需掌握所学各种图形的特性及它们之间的关系。
8.B
【分析】根据题意可知,这个三角形有一个角是直角,且两个底角相等。根据三角形的内角和为180°可知,两个底角不可能都是直角,则顶角是直角,两个底角为(180°-90°)÷2=45°。
【详解】由分析得:
90°+90°=180°,则底角不可能是直角,顶角是直角,即90°。
故答案为:B。
【点睛】本题考查三角形的分类以及三角形的内角和定理,本题关键是明确等腰直角三角形中顶角是直角。
9. 3 3 7
【分析】至少要用3根硬纸条,因为三角形有3条边。至少要用3颗图钉,因为三角形有3个顶点。三角形的三边关系:三角形的任意两边之和大于第三边,任意两边之差小于第三边。
【详解】由分析得:
小亮准备用图钉固定硬纸条做一个三角形。他最少应准备3根硬纸条,准备3个图钉。
5-3<第三条边<3+5,2<第三条边<8,则另一根硬纸条最长为7cm。
【点睛】熟练掌握三角形的概念以及三角形的三边关系是解答此题的关键。
10. 16 8
【分析】三角形三边关系:三角形任意两边的和大于第三边,任意两边之差小于第三边。
据此,我们可分别计算出已知两边的和与差,然后在和与差的取值范围之间确定第三边最长和最短的长度。
【详解】12-5<第三边的长度<12+5,即7<第三边的长度<17,那么第三边最长是16cm,最短是8cm。
【点睛】结合三边关系,恰好可以把第三边的长度固定在两个数的和与差之间,又因为取整厘米数,所以能够得到最长和最短的长度。
11. 稳定性 自行车的三角形车架
【分析】三角形稳定性是指三角形具有稳定性,有着稳固、坚定、耐压的特点,如埃及金字塔、钢轨、三角形框架、起重机、三角形吊臂、屋顶、三角形钢架、钢架桥和埃菲尔铁塔都以三角形形状建造。
【详解】斜拉桥等建筑是利用三角形的稳定性设计的,生活中的自行车的三角形车架也利用了这一原理。
【点睛】本题考查了学生对三角形的稳定性的掌握与运用。
12.(1)80
(2)90
(3)33
【分析】(1)根据三角形的内角和等于180°,即∠1+∠2+∠3=180°,∠3=180°-∠1-∠2=180°-35°-65°=80°,据此解答;
(2)根据三角形的内角和等于180°,即∠1+∠2+∠3=180°,∠3=180°-∠1-∠2=180°-75°-15°=90°,据此解答;
(3)根据三角形的内角和等于180°,即∠1+∠2+∠3=180°,∠3=180°-∠1-∠2=180°-102°-45°=33°,据此解答即可。
(1)由分析可知,∠3=180°-∠1-∠2=180°-35°-65°=80°
(2)由分析可知,∠3=180°-∠1-∠2=180°-75°-15°=90°
(3)由分析可知,∠3=180°-∠1-∠2=180°-102°-45°=33°
【点睛】本题考查了三角形内角和的应用。
13.(1)6
(2) 6 7
【分析】根据三角形的特征:任意两边之和大于第三边,任意两边之差小于第三边;由此解答即可。
(1)当从3cm处剪开,则三段长度为2cm,1cm,7cm,不能组成三角形;当从4cm处剪开,则三段长度为2cm,2cm,6cm,不能组成三角形;当从5cm处剪开,则三段长度为2cm,3cm,5cm,不能组成三角形;当从6cm处剪开,则三段长度为2cm,4cm,4cm,能组成三角形。
(2)当从4cm处剪开,则三段长度为3cm,1cm,6cm,不能组成三角形;当从5cm处剪开,则三段长度为2cm,3cm,5cm,不能组成三角形;当从6cm处剪开,则三段长度为3cm,3cm,4cm,能组成三角形;当从7cm处剪开,则三段长度为3cm,4cm,3cm,能组成三角形。
【点睛】本题考查了学生对三角形三边关系的理解和灵活运用。
14. 80° 30° 119°
【分析】根据三角形的内角和为180°可知,第一幅图中,∠C=180°-∠A-∠B。第二幅图中,∠B=180°-∠A-∠C,∠A为90°。第三幅图中,∠C=180°-∠A-∠B。
【详解】第一幅图:∠C=180°-50°-50°=80°。
第二幅图:∠B=180°-90°-60°=30°。
第三幅图:∠C=180°-32°-29°=119°。
【点睛】明确三角形的内角和是180°是解答此题的关键。
15. 24 38
【分析】图①周长为(4+5+3×1)cm,图③周长为(4+5+3×3)cm,图⑤周长为(4+5+3×5)cm,得出第单数幅图周长=(4+5+3×单数)cm。图②周长为(4+4+3×2)cm, 图④周长为(4+4+3×4)cm,得出第双数幅图周长=(4+4+3×双数)cm。据此解答即可。
【详解】4+5+3×5
=4+5+15
=9+15
=24(cm)
第⑤幅图周长是24cm。
4+4+3×10
=4+4+30
=8+30
=38(cm)
第⑩幅图周长是38cm。
【点睛】本题关键是求出已知图形周长之间的规律,再根据这个规律解决问题。
16. 3 三角
【分析】根据梯形的定义可知:梯形的两个底互相平行且不相等,如果将上底延长3厘米,则上底变成5+3=8厘米,与下底相等了,由此根据一组对边平行且相等的四边形是平行四边形,故上底延长3厘米后,就是平行四边形;当上底缩短5厘米时,5-5=0,即上底缩为一个点,此时梯形变为三角形,据此解答。
【详解】根据分析得,若将上底延长3厘米,它就变成平行四边形;若将上底缩短5厘米,它就变成三角形。
【点睛】本题考查了梯形与平行四边形的定义与性质,及三角形的特点,注意:一组对边平行且相等的四边形是平行四边形。
17.71厘米
【分析】三角形的三边关系:两边之和大于第三边,两边的差一定小于第三边;用35减去10的差再加上1,求出第三条边最短的长度;再用求出的第三条边最短的长度加上35再加上10,求出这个三角形风筝的周长最少是多少厘米。
【详解】35-10=25(厘米)
25+1=26(厘米)
26+35+10
=61+10
=71(厘米)
答:这个三角形风筝的周长最少是71厘米。
【点睛】因为两边之差要小于第三边且边长取整厘米数,所以第三边最小是26厘米,这是解答此题的关键。
18.3分米、4分米、5分米、6分米或7分米。
【分析】根据三角形的特征:任意两边之和大于第三边,任意两边之差小于第三边;由此解答即可。
【详解】3+5=8(分米)
5-3=2(分米)
2分米<第三根木条的长度<8分米
答:第三根木条的长度可能是3分米、4分米、5分米、6分米或7分米。
【点睛】解决此题关键是根据三角形的特性进行分析、解答。
19.画图见详解;底长:16厘米;腰长:20厘米
【分析】等腰三角形的两条腰相等。2×腰+底=56厘米。腰比底长4厘米,则用周长加上4厘米,即为3条腰的长度。腰为(56+4)÷3厘米。再用腰减去4厘米,即可求出底的长度。
【详解】
(56+4)÷3
=60÷3
=20(厘米)
20-4=16(厘米)
答:它的底长是16厘米,腰长是20厘米。
【点睛】本题考查等腰三角形的性质,要根据等腰三角形两腰相等的特点进行分析,画出线段图,即可得出结论。
20.62米
【分析】如下图,把下底靠墙这样需要用的篱笆最少,需要的篱笆长度为上底加两腰的长度和,据此解答。
【详解】画图如下:
18+22×2
=18+44
=62(米)
答:围这块菜地最少需要用篱笆62米。
【点睛】要使需要的篱笆最少,就要使梯形菜地最长的边靠墙,这是解答本题的关键。
21.底角72°;底角36°
【分析】等腰三角形的两个底角相等。根据三角形的内角和为180°可知,顶角+2×底角=180°。根据“底角是顶角的2倍”,则5个顶角是180°,顶角为180°÷5。再用顶角乘2,即可求出底角。
【详解】180°÷(1+2+2)
=180°÷5
=36°
36°×2=72°
答:这个等腰三角形的底角和顶角分别是72°和36°。
【点睛】本题考查等腰三角形的性质和三角形的内角和,关键是明确5个顶角是180°。
22.∠B:55°;∠C:50°
【分析】三角形的内角和是180°,用180°减去35°再减去90°,求出∠B的度数;用180°减去40°再减去90°,求出∠C的度数。
【详解】180°-35°-90°
=145°-90°
=55°
180°-40°-90°
=140°-90°
=50°
答:∠B的度数是55°,∠C的度数50°。
【点睛】解答此题的关键是明确三角形的内角和是180°。
23.图见分析;540°
【分析】如下图,把五边形分成3个三角形,3个三角形的内角和等于五边形的内角和,据此即可解答。
【详解】如上图,把五边形分成3个三角形。
180°×3=540°
答:五边形的内角和是540°。
【点睛】本题主要考查学生的综合分析和动手作图能力。
24.720°
【分析】六边形分割成了4个三角形,然后根据n边形的内角的和公式(n-2)×180°解答即可。
【详解】(6-2)×180°
=4×180°
=720°
答:六边形的内角和是720°。
【点睛】本题考查了多边形的内角和公式的推导,求出过同一个顶点把多边形分成的三角形的个数是解题的关键,也是本题的难点。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第七单元三角形、平行四边形和梯形开学前复习巩固自检卷(单元测试)-小学数学四年级下册苏教版
一、选择题
1.如果三角形的两边分别是4厘米、8厘米,则第三条边不可能是( )。
A.6厘米 B.5厘米 C.4厘米 D.11厘米
2.亮亮想知道下面三角形ABC三个内角度数的和,下面拼法中正确的是( )。
A. B. C.
3.以下是几组小棒的长度,可以摆成三角形的是( )。
A.3cm、5cm、2cm B.7cm、8cm、1cm
C.10cm、5cm、8cm D.4cm、13cm、7cm
4.下面说法正确的有( )个。
①三角形具有稳定性。
②三角形越大,该三角形的内角和就越大。
③我画了一个三角形,其中最小的角是61°。
④用3根分别长1cm、2cm、3cm的小棒,一定可以拼成一个三角形。
A.1 B.2 C.3 D.4
5.如图,已知a∥b,所以图中有( )个梯形。
A.4个 B.3个 C.2个 D.1个
6.如图所示的三角形被挡住了一个角,这是一个( )三角形。
A.锐角 B.钝角 C.直角 D.等腰
7.下面图形的分类图中,不正确的是( )。
A. B.
C. D.
8.一个三角形,既是直角三角形,又是等腰三角形。它的顶角是多少度?( )
A.60° B.90° C.45°
二、填空题
9.小亮准备用图钉固定硬纸条做一个三角形。他最少应准备( )根硬纸条,准备( )个图钉。如果其中2根硬纸条分别长3cm和5cm,那么另一根硬纸条最长为( )cm。(填整数)
10.一个三角形三条边的长度都是整厘米数,其中两条边分别长5cm和12cm,那么第三条边最长是( )cm,最短是( )cm。
11.斜拉桥等建筑是利用三角形的( )设计的,生活中的( )也利用了这一原理。
12.在下列三角形中,∠1,∠2,∠3是三角形的三个内角,求∠3的度数。
(1)若∠1=35°,∠2=65°,那么∠3=( )°;
(2)若∠1=75°,∠2=15°,那么∠3=( )°;
(3)若∠1=102°,∠2=45°,那么∠3=( )°。
13.下图是一根长10cm的吸管。(填整数)
(1)如果第一次从2cm处剪开,第二次从( )cm处剪开,剪成的3小段正好可以围成三角形。
(2)如果第一次从3cm处剪开,第二次可以从( )cm处剪开,也可以从( )cm处剪开,剪成的3小段正好可以围成一个三角形。
14.求出下面每个三角形中未知角的度数。
∠C=( )
∠B=( )
∠C=( )
15.用相同的直角三角形进行拼图游戏(如下图),请观察图中的拼图规律,第⑤幅图的周长是( )cm,照这样排下去,第⑩幅图的周长是( )cm。
16.一个梯形上底长5厘米,下底宽8厘米。若将上底延长( )厘米它就变成平行四边形;若将上底缩短5厘米它就变成( )形。
三、解答题
17.王婷想做一个三角形的风筝。已知其中两条边长分别是35厘米、10厘米,这个三角形风筝的周长最少是多少厘米?(长度取整厘米数)
18.小刚想给他的小狗做一个房子,房顶的框架要做成三角形,其中一根木条长3分米,另一根长5分米,那么第三根木条的长度可能是多少分米?(长度取整分米数)
19.一个等腰三角形的周长是56厘米,腰比底长4厘米。它的底长和腰长各是多少厘米?(先画图,再解答)
20.赵大伯准备靠墙围一块梯形菜地,菜地的上底是18米,下底是32米,两条腰都是22米。已知墙的长度大于32米,则围这块菜地最少需要用篱笆多少米?(先画图,再解答)
21.一个等腰三角形的底角是顶角的2倍,这个等腰三角形的底角和顶角分别是多少?
22.如图所示,已知∠1=40°,∠2=35°,求∠B和∠C的度数。
23.已知三角形的内角和是180°。下面的五边形的内角和是多少度?我们可以先把这个五边形分成几个三角形后,就能方便地算出它的内角和。请你在图上画一画,然后再一算。
24.三角形的内角和是180°,将这个四边形这样分割如图1,就可以算出四边形内角和:180°×2=360°
我也用这样的方法计算五边形的内角:180°×3=540°,如图2。
请你用同样的方法计算图3六边形的内角和。
参考答案:
1.C
【分析】根据三角形两边之和大于第三边,两边之差小于第三边,解答此题即可。
【详解】8-4=4(厘米)
8+4=12(厘米)
4厘米<第三边<12厘米
故答案为:C
【点睛】熟练掌握三角形的三边关系,是解答此题的关键。
2.C
【分析】要想知道三个内角度数的和,将三个内角组合成一个角才能利用量角器量出来,据此即可解答。
【详解】A.三个角中间有空隙,没有组成一个角,
B.三个角中间有空隙,没有组成一个角,
C.三个角中间没有空隙,组成一个角,可以测量,
故答案为:C
【点睛】本题考查了学生对内角和的认识和理解。
3.C
【分析】根据三角形的三边关系:两边之和大于第三边,三角形的两边的差一定小于第三边;进行依次分析即可。
【详解】A.3+2=5,不能围成三角形;
B.1+7=8,不能围成三角形;
C.5+8>10,能围成三角形;
D.4+7<13,不能围成三角形。
故答案为:C
【点睛】熟练掌握三角形的三边关系是解答此题的关键。
4.A
【分析】三角形具有稳定性;三角形的内角和是180°;三角形的三边关系:两边之和大于第三条边,两边之差小于第三条边。
【详解】①三角形具有稳定性,原题说法正确。
②任意三角形的内角和都是180°,原题说法错误。
③一个三角形,最小的角不一定就是61°,还可以更小的角,只要满足三角形的内角和是180°即可,原题说法错误。
④1+2=3,则长1cm、2cm、3cm的小棒,一定不可以拼成一个三角形;原题说法错误。
故答案为:A
【点睛】本题主要考查了学生对三角形具有稳定性、三角形的内角和定律、三角形的三边关系的掌握与理解。
5.B
【分析】梯形是只有一组对边平行的四边形,观察题图可知,四边形ADEB、四边形BEFC及四边形ADFC都是梯形,据此解答。
【详解】由分析得:图中一共有3个梯形。
故答案为:B
【点睛】本题考查梯形的特征,需熟练掌握。
6.B
【分析】先用量角器测量出已知的两个角的度数,再根据三角形的内角和,用180°依次减去已知两个角的度数,求出被挡住角的度数,进而判断这个三角形是什么三角形。
【详解】180°-35°-40°=105°
则被挡住的角是一个钝角,这个三角形是一个钝角三角形。
故答案为:B。
【点睛】本题关键是根据三角形的内角和求出被挡住角的度数。
7.D
【分析】三角形中,两条腰相等的三角形是等腰三角形,三条边相等的三角形是等腰三角形,则等边三角形是特殊的等腰三角形。平行四边形的两组对边平行,长方形的两组对边平行,4个角都是直角,正方形的两组对边平行,4个角都是直角,4条边相等,则正方形是特殊的长方形,长方形是特殊的平行四边形。锐角三角形不是特殊的钝角三角形,也不是特殊的直角三角形。平行四边形和梯形都是四边形,但是平行四边形不是特殊的梯形。
【详解】A.分类图正确;
B. 分类图正确;
C. 分类图正确;
D. 分类图不正确;
故答案为:D。
【点睛】本题考查三角形、四边形的分类,需掌握所学各种图形的特性及它们之间的关系。
8.B
【分析】根据题意可知,这个三角形有一个角是直角,且两个底角相等。根据三角形的内角和为180°可知,两个底角不可能都是直角,则顶角是直角,两个底角为(180°-90°)÷2=45°。
【详解】由分析得:
90°+90°=180°,则底角不可能是直角,顶角是直角,即90°。
故答案为:B。
【点睛】本题考查三角形的分类以及三角形的内角和定理,本题关键是明确等腰直角三角形中顶角是直角。
9. 3 3 7
【分析】至少要用3根硬纸条,因为三角形有3条边。至少要用3颗图钉,因为三角形有3个顶点。三角形的三边关系:三角形的任意两边之和大于第三边,任意两边之差小于第三边。
【详解】由分析得:
小亮准备用图钉固定硬纸条做一个三角形。他最少应准备3根硬纸条,准备3个图钉。
5-3<第三条边<3+5,2<第三条边<8,则另一根硬纸条最长为7cm。
【点睛】熟练掌握三角形的概念以及三角形的三边关系是解答此题的关键。
10. 16 8
【分析】三角形三边关系:三角形任意两边的和大于第三边,任意两边之差小于第三边。
据此,我们可分别计算出已知两边的和与差,然后在和与差的取值范围之间确定第三边最长和最短的长度。
【详解】12-5<第三边的长度<12+5,即7<第三边的长度<17,那么第三边最长是16cm,最短是8cm。
【点睛】结合三边关系,恰好可以把第三边的长度固定在两个数的和与差之间,又因为取整厘米数,所以能够得到最长和最短的长度。
11. 稳定性 自行车的三角形车架
【分析】三角形稳定性是指三角形具有稳定性,有着稳固、坚定、耐压的特点,如埃及金字塔、钢轨、三角形框架、起重机、三角形吊臂、屋顶、三角形钢架、钢架桥和埃菲尔铁塔都以三角形形状建造。
【详解】斜拉桥等建筑是利用三角形的稳定性设计的,生活中的自行车的三角形车架也利用了这一原理。
【点睛】本题考查了学生对三角形的稳定性的掌握与运用。
12.(1)80
(2)90
(3)33
【分析】(1)根据三角形的内角和等于180°,即∠1+∠2+∠3=180°,∠3=180°-∠1-∠2=180°-35°-65°=80°,据此解答;
(2)根据三角形的内角和等于180°,即∠1+∠2+∠3=180°,∠3=180°-∠1-∠2=180°-75°-15°=90°,据此解答;
(3)根据三角形的内角和等于180°,即∠1+∠2+∠3=180°,∠3=180°-∠1-∠2=180°-102°-45°=33°,据此解答即可。
(1)由分析可知,∠3=180°-∠1-∠2=180°-35°-65°=80°
(2)由分析可知,∠3=180°-∠1-∠2=180°-75°-15°=90°
(3)由分析可知,∠3=180°-∠1-∠2=180°-102°-45°=33°
【点睛】本题考查了三角形内角和的应用。
13.(1)6
(2) 6 7
【分析】根据三角形的特征:任意两边之和大于第三边,任意两边之差小于第三边;由此解答即可。
(1)当从3cm处剪开,则三段长度为2cm,1cm,7cm,不能组成三角形;当从4cm处剪开,则三段长度为2cm,2cm,6cm,不能组成三角形;当从5cm处剪开,则三段长度为2cm,3cm,5cm,不能组成三角形;当从6cm处剪开,则三段长度为2cm,4cm,4cm,能组成三角形。
(2)当从4cm处剪开,则三段长度为3cm,1cm,6cm,不能组成三角形;当从5cm处剪开,则三段长度为2cm,3cm,5cm,不能组成三角形;当从6cm处剪开,则三段长度为3cm,3cm,4cm,能组成三角形;当从7cm处剪开,则三段长度为3cm,4cm,3cm,能组成三角形。
【点睛】本题考查了学生对三角形三边关系的理解和灵活运用。
14. 80° 30° 119°
【分析】根据三角形的内角和为180°可知,第一幅图中,∠C=180°-∠A-∠B。第二幅图中,∠B=180°-∠A-∠C,∠A为90°。第三幅图中,∠C=180°-∠A-∠B。
【详解】第一幅图:∠C=180°-50°-50°=80°。
第二幅图:∠B=180°-90°-60°=30°。
第三幅图:∠C=180°-32°-29°=119°。
【点睛】明确三角形的内角和是180°是解答此题的关键。
15. 24 38
【分析】图①周长为(4+5+3×1)cm,图③周长为(4+5+3×3)cm,图⑤周长为(4+5+3×5)cm,得出第单数幅图周长=(4+5+3×单数)cm。图②周长为(4+4+3×2)cm, 图④周长为(4+4+3×4)cm,得出第双数幅图周长=(4+4+3×双数)cm。据此解答即可。
【详解】4+5+3×5
=4+5+15
=9+15
=24(cm)
第⑤幅图周长是24cm。
4+4+3×10
=4+4+30
=8+30
=38(cm)
第⑩幅图周长是38cm。
【点睛】本题关键是求出已知图形周长之间的规律,再根据这个规律解决问题。
16. 3 三角
【分析】根据梯形的定义可知:梯形的两个底互相平行且不相等,如果将上底延长3厘米,则上底变成5+3=8厘米,与下底相等了,由此根据一组对边平行且相等的四边形是平行四边形,故上底延长3厘米后,就是平行四边形;当上底缩短5厘米时,5-5=0,即上底缩为一个点,此时梯形变为三角形,据此解答。
【详解】根据分析得,若将上底延长3厘米,它就变成平行四边形;若将上底缩短5厘米,它就变成三角形。
【点睛】本题考查了梯形与平行四边形的定义与性质,及三角形的特点,注意:一组对边平行且相等的四边形是平行四边形。
17.71厘米
【分析】三角形的三边关系:两边之和大于第三边,两边的差一定小于第三边;用35减去10的差再加上1,求出第三条边最短的长度;再用求出的第三条边最短的长度加上35再加上10,求出这个三角形风筝的周长最少是多少厘米。
【详解】35-10=25(厘米)
25+1=26(厘米)
26+35+10
=61+10
=71(厘米)
答:这个三角形风筝的周长最少是71厘米。
【点睛】因为两边之差要小于第三边且边长取整厘米数,所以第三边最小是26厘米,这是解答此题的关键。
18.3分米、4分米、5分米、6分米或7分米。
【分析】根据三角形的特征:任意两边之和大于第三边,任意两边之差小于第三边;由此解答即可。
【详解】3+5=8(分米)
5-3=2(分米)
2分米<第三根木条的长度<8分米
答:第三根木条的长度可能是3分米、4分米、5分米、6分米或7分米。
【点睛】解决此题关键是根据三角形的特性进行分析、解答。
19.画图见详解;底长:16厘米;腰长:20厘米
【分析】等腰三角形的两条腰相等。2×腰+底=56厘米。腰比底长4厘米,则用周长加上4厘米,即为3条腰的长度。腰为(56+4)÷3厘米。再用腰减去4厘米,即可求出底的长度。
【详解】
(56+4)÷3
=60÷3
=20(厘米)
20-4=16(厘米)
答:它的底长是16厘米,腰长是20厘米。
【点睛】本题考查等腰三角形的性质,要根据等腰三角形两腰相等的特点进行分析,画出线段图,即可得出结论。
20.62米
【分析】如下图,把下底靠墙这样需要用的篱笆最少,需要的篱笆长度为上底加两腰的长度和,据此解答。
【详解】画图如下:
18+22×2
=18+44
=62(米)
答:围这块菜地最少需要用篱笆62米。
【点睛】要使需要的篱笆最少,就要使梯形菜地最长的边靠墙,这是解答本题的关键。
21.底角72°;底角36°
【分析】等腰三角形的两个底角相等。根据三角形的内角和为180°可知,顶角+2×底角=180°。根据“底角是顶角的2倍”,则5个顶角是180°,顶角为180°÷5。再用顶角乘2,即可求出底角。
【详解】180°÷(1+2+2)
=180°÷5
=36°
36°×2=72°
答:这个等腰三角形的底角和顶角分别是72°和36°。
【点睛】本题考查等腰三角形的性质和三角形的内角和,关键是明确5个顶角是180°。
22.∠B:55°;∠C:50°
【分析】三角形的内角和是180°,用180°减去35°再减去90°,求出∠B的度数;用180°减去40°再减去90°,求出∠C的度数。
【详解】180°-35°-90°
=145°-90°
=55°
180°-40°-90°
=140°-90°
=50°
答:∠B的度数是55°,∠C的度数50°。
【点睛】解答此题的关键是明确三角形的内角和是180°。
23.图见分析;540°
【分析】如下图,把五边形分成3个三角形,3个三角形的内角和等于五边形的内角和,据此即可解答。
【详解】如上图,把五边形分成3个三角形。
180°×3=540°
答:五边形的内角和是540°。
【点睛】本题主要考查学生的综合分析和动手作图能力。
24.720°
【分析】六边形分割成了4个三角形,然后根据n边形的内角的和公式(n-2)×180°解答即可。
【详解】(6-2)×180°
=4×180°
=720°
答:六边形的内角和是720°。
【点睛】本题考查了多边形的内角和公式的推导,求出过同一个顶点把多边形分成的三角形的个数是解题的关键,也是本题的难点。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
