【强化训练】沪教版(上海)九下 第二十八章统计初步定向测评试题(含解析)
文档属性
| 名称 | 【强化训练】沪教版(上海)九下 第二十八章统计初步定向测评试题(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-24 08:28:54 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
九年级数学第二学期第二十八章统计初步定向测评
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内 ( http: / / www.21cnjy.com )相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。2·1·c·n·j·y
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、某校“安全知识”比赛有16名 ( http: / / www.21cnjy.com )同学参加,规定前8名的同学进入决赛.若某同学想知道自己能否晋级,不仅要了解自己的成绩,还需要了解16名参赛同学成绩的( )21·世纪*教育网
A.平均数 B.中位数 C.众数 D.方差
2、某校八年级人数相等的甲、乙、丙三个班,同时参加了一次数学测试,对成绩进行了统计分析,平均分都是72分,方差分别为,,,则成绩波动最小的班级( )
A.甲 B.乙 C.丙 D.无法确定
3、鞋厂生产不同号码的鞋,其中,生产数量最多的鞋号是调查不同年龄的人的鞋号所构成的数据的( )
A.平均数 B.众数 C.中位数 D.众数或中位数
4、下列调查中,其中适合采用抽样调查的是( )
A.调查某班50名同学的视力情况
B.为了解新型冠状病毒(SARS-CoV-2)确诊病人同一架飞机乘客的健康情况
C.为保证“神舟9号”成功发射,对其零部件进行检查
D.检测中卫市的空气质量
5、下列说法中,正确的是( )
A.若,,则
B.90′=1.5°
C.过六边形的每一个顶点有4条对角线
D.疫情防控期间,要掌握进入校园人员的体温是否正常,可采用抽样调查
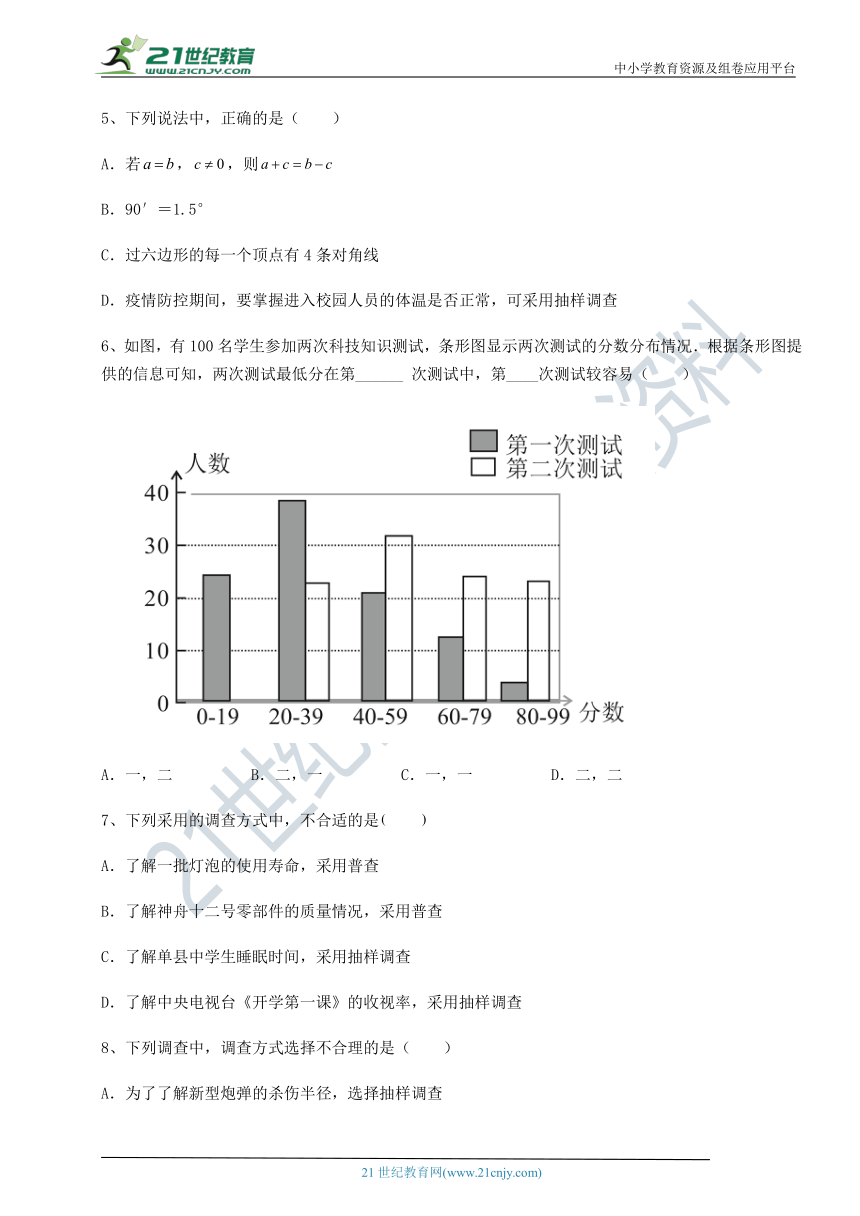
6、如图,有100名学生 ( http: / / www.21cnjy.com )参加两次科技知识测试,条形图显示两次测试的分数分布情况.根据条形图提供的信息可知,两次测试最低分在第______ 次测试中,第____次测试较容易( )
( http: / / www.21cnjy.com / )
A.一,二 B.二,一 C.一,一 D.二,二
7、下列采用的调查方式中,不合适的是
A.了解一批灯泡的使用寿命,采用普查
B.了解神舟十二号零部件的质量情况,采用普查
C.了解单县中学生睡眠时间,采用抽样调查
D.了解中央电视台《开学第一课》的收视率,采用抽样调查
8、下列调查中,调查方式选择不合理的是( )
A.为了了解新型炮弹的杀伤半径,选择抽样调查
B.为了了解某河流的水质情况,选择普查
C.为了了解神舟飞船的设备零件的质量情况,选择普查
D.为了了解一批袋装食品是否含有防腐剂,选择抽样调查
9、一组数据的最大值为105,最小值为23,若确定组距为9,则分成的组数为( )
A.11 B.10 C.9 D.8
10、小明抛一枚硬币100次,其中有60次正面朝上,则反面朝上的频率是( )
A.0.6 B.6 C.0.4 D.4
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、如图是某同学6次数学测验成绩的折线统计图,则该同学这6次成绩最高分与最低分的差是_________分.21教育名师原创作品
( http: / / www.21cnjy.com / )
2、小丽的笔试成绩为90分,面试成绩为95分,若笔试成绩、面试成绩按6:4计算平均成绩,则小丽的平均成绩是 _______分.
3、小刘和小李参加射击训练,各射击10次的平均成绩相同,如果他们射击成绩的方差分别是,,那么两人中射击成绩比较稳定的是_________.
4、已知一组数据,,,它们的平均数是,则______,这一组数据的方差为______.
5、一组数据:6,4,10的权数分别是2,5,1,则这组数据的加权平均数是______.
三、解答题(5小题,每小题10分,共计50分)
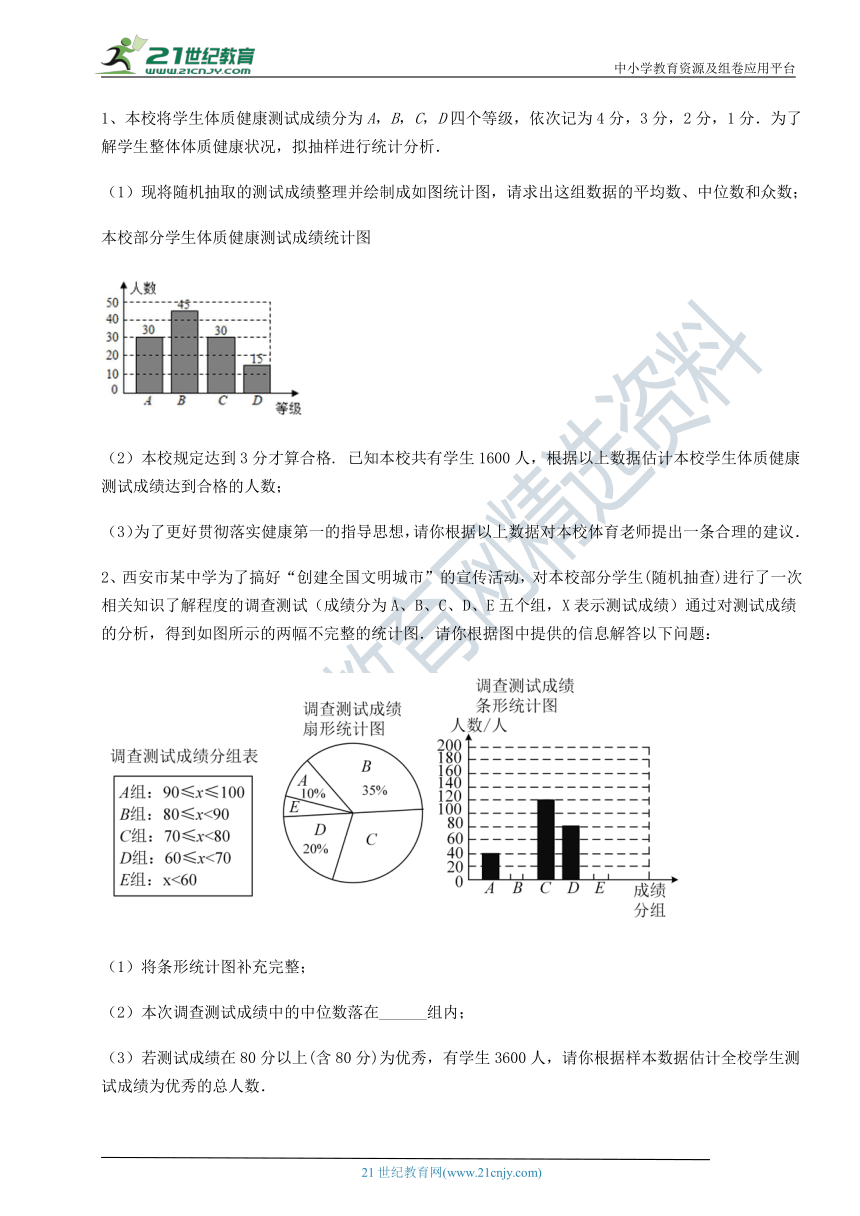
1、本校将学生体质健康测试成绩分为A,B,C,D四个等级,依次记为4分,3分,2分,1分.为了解学生整体体质健康状况,拟抽样进行统计分析.
(1)现将随机抽取的测试成绩整理并绘制成如图统计图,请求出这组数据的平均数、中位数和众数;
本校部分学生体质健康测试成绩统计图
( http: / / www.21cnjy.com / )
(2)本校规定达到3分才算合格. 已知本校共有学生1600人,根据以上数据估计本校学生体质健康测试成绩达到合格的人数;
(3)为了更好贯彻落实健康第一的指导思想,请你根据以上数据对本校体育老师提出一条合理的建议.
2、西安市某中学为了搞好“创建全 ( http: / / www.21cnjy.com )国文明城市”的宣传活动,对本校部分学生(随机抽查)进行了一次相关知识了解程度的调查测试(成绩分为A、B、C、D、E五个组,X表示测试成绩)通过对测试成绩的分析,得到如图所示的两幅不完整的统计图.请你根据图中提供的信息解答以下问题:
( http: / / www.21cnjy.com / )
(1)将条形统计图补充完整;
(2)本次调查测试成绩中的中位数落在______组内;
(3)若测试成绩在80分以上(含80分)为优秀,有学生3600人,请你根据样本数据估计全校学生测试成绩为优秀的总人数.21cnjy.com
3、至善中学七年一班期中考试数学成绩平均分 ( http: / / www.21cnjy.com )为84.75,该班小明的数学成绩为92分,把92与84.75的差叫做小明数学成绩的离均差,即小明数学成绩的离均差为+7.25.2-1-c-n-j-y
(1)该班小丽的数学成绩为82分,求小丽数学成绩的离均差.
(2)已知该班第一组8名同学数学成绩的离均差分别为:
+10.25,﹣8.75,+31.25,+15.25,﹣3.75,﹣12.75,﹣10.75,﹣32.75.
①求这组同学数学成绩的最高分和最低分;
②求这组同学数学成绩的平均分;
③若该组数学成绩最低的同学达到及格的72分,则该组数学成绩的平均分是否达到或超过班平均分?超过或低于多少分?
4、为积极响应“弘扬传统文化 ( http: / / www.21cnjy.com )”的号召,某校倡导全校1200名学生进行经典诗词诵背活动,并在活动之后举办经典诗词大赛,为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取部分学生调查“一周诗词诵背数量”.根据调查结果绘制成的统计图(部分)如下图所示:
( http: / / www.21cnjy.com / )
大赛结束后一个月,再次抽查这部分学生“一周诗词诵背数量”,绘制成统计表:
一周诗词诵背数量 3首 4首 5首 6首 7首 8首
人数 10 10 15 40 25 20
请根据调查的信息分析:
(1)补全频数分布直方图.
(2)活动启动之初学生“一周诗词诵背数量”的中位数为______首.
(3)估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数.
(4)选择适当的统计量,从某一个角度分析两次调查的相关数据,评价该校经典诗词诵背系列活动的效果.
5、为深入开展青少年毒品预防教育工 ( http: / / www.21cnjy.com )作,增强学生禁毒意识,某校联合禁毒办组织开展了“2021青少年禁毒知识竞赛”活动,并随即抽查了部分同学的成绩,整理并制作成图表如下:
( http: / / www.21cnjy.com / ) ( http: / / www.21cnjy.com / )
根据以上图表提供的信息,回答下列问题:
(1)抽查的人数为______人,______;
(2)请补全频数分布直方图;
(3)若成绩在80分以上(包括80分)为“优秀”,请你估计该校2400名学生中竞赛成绩是“优秀”的有多少名?www-2-1-cnjy-com
-参考答案-
一、单选题
1、B
【分析】
由中位数的概念,即最中间一个或两个数据的平均 ( http: / / www.21cnjy.com )数;可知16人成绩的中位数是第8名和第9名的成绩.根据题意可得:参赛选手要想知道自己是否能进入前8名,只需要了解自己的成绩以及全部成绩的中位数,比较即可.
【详解】
解:由于16个人中,第8和 ( http: / / www.21cnjy.com )第9名的成绩的平均数是中位数,故同学知道了自己的分数后,想知道自己能否进入决赛,还需知道这16位同学的成绩的中位数.
故选:B.
【点睛】
此题主要考查统计的有关知识,主要包括 ( http: / / www.21cnjy.com )平均数、中位数、众数的意义.反映数据集中程度的统计量有平均数、中位数、众数等,各有局限性,因此要对统计量进行合理的选择和恰当的运用.
2、C
【分析】
根据方差的意义可作出判断.方差是用 ( http: / / www.21cnjy.com )来衡量一组数据波动大小的量,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
【详解】
解:∵,,,
∴,
∴成绩波动最小的班级是:丙班.
故选:C.
【点睛】
此题主要考查了方差的意义,正确理解方差的意义是解题关键.
3、B
【分析】
由鞋厂关心的数据,即大众买的最多的鞋号,也就是出现次数最多的数据,从而可得所构成的数据是众数.
【详解】
解:生产数量最多的鞋号是调查不同年龄的人的鞋号所构成的数据的众数,
故选B
【点睛】
本题考查的是众数的含义及众数表示的意义,理解众数的含义及在生活中的应用是解本题的关键.
4、D
【分析】
抽样调查是通过对样本调查来估计总体特征,其调查结果是近似的;而全面调查得到的结果比较准确;根据对调查结果的要求对选项进行判断.
【详解】
A调查某班50名同学的视力情况,人数较少,应采用全面调查,故不符合要求;
B为了解新型冠状病毒确诊病人同一架飞机乘客的健康状况,意义重大,应采用全面调查,故不符合要求;
C为保证“神州9号”成功发射,对零部件进行检查,意义重大,应采用全面调查,故不符合要求;
D检查中卫市的空气质量,应采用抽样调查,故符合要求;
故选D.
【点睛】
本题考察了抽样调查与全面调查.解题的关键与难点在于理清对调查结果的要求.
5、B
【分析】
由等式的基本性质可判断A,由 可判断B,由过边形的一个顶点可作条对角线可判断C,由全面调查与抽样调查的含义可判断D,从而可得答案.【版权所有:21教育】
【详解】
解:若,则故A不符合题意;
90′=故B符合题意;
过六边形的每一个顶点有3条对角线,故C不符合题意;
疫情防控期间,要掌握进入校园人员的体温是否正常,事关重大,一定采用全面调查,故D不符合题意;
故选:B.
【点睛】
本题考查的是等式的基本性质,角度的换算,多边形的对角线问题,全面调查与抽样调查的含义,掌握以上基础知识是解本题的关键.
6、A
【分析】
根据条形统计图,发现最低分显然在第一次测验中;因为第二次测验的高分人数较多,所以第二次测验较容易.
【详解】
解:根据条形统计图,发现最低分在第一次测验中;因为第二次测验的高分人数较多,所以第二次测验较容易.
故选A.
【点睛】
条形统计图能清楚地表示出每个项目的数据,能够根据条形统计图读懂两者分别表示的意义是关键.
7、A
【分析】
根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似解答即可.21教育网
【详解】
解:A、了解一批灯泡的使用寿命,采用抽样调查,本选项说法不合适,符合题意;
、了解神舟十二号零部件的质量情况,采用普查,本选项说法合适,不符合题意;
、了解单县中学生睡眠时间,采用抽样调查,本选项说法合适,不符合题意;
、了解中央电视台《开学第一课》的收视率,采用抽样调查,本选项说法合适,不符合题意;
故选:A.
【点睛】
本题考查的是抽样调查和全面调查,选择普查还 ( http: / / www.21cnjy.com )是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.【来源:21·世纪·教育·网】
8、B
【分析】
根据调查的不同目的来选择全面调查或抽样调查,再判断四个选项即可.
【详解】
解:A选项,C选项,D选项选择调查方式合理,故A选项,C选项,D选项不符合题意.
B选项,为了了解某河流的水质情况,选择普查耗费人力,物力和时间较多,而选择抽样调查更加节约,且和普查的结果相差不大,故B选项符合题意.
故选:B.
【点睛】
本题考查全面调查和抽样调查,对于具有破坏性 ( http: / / www.21cnjy.com )的调查、无法进行全面调查、全面调查的意义或价值不大时,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用全面调查.
9、B
【分析】
极差除以组距,大于或等于该值的最小整数即为组数.
【详解】
解:,
分10组.
故选:B.
【点睛】
本题考查了组距的划分,一般分为组最科学.
10、C
【分析】
先求出反面朝上的频数,然后根据频率=频数÷总数求解即可
【详解】
解:∵小明抛一枚硬币100次,其中有60次正面朝上,
∴小明抛一枚硬币100次,其中有40次反面朝上,
∴反面朝上的频率=40÷100=0.4,
故选C.
【点睛】
本题主要考查了根据频数求频率,解题的关键在于能够熟练掌握频率=频数÷总数.
二、填空题
1、25
【分析】
先从统计图中读出这6次成绩的最高分与最低分,然后相减即可.
【详解】
解:根据折线统计图可知,这6次成绩分别是(单位:分):
65,75,60,80,70,85
其中,最高分是85分,最低分是60分,
所以,最高分与最低分的差是85-60=25(分).
故答案为:25.
【点睛】
本题考查了折线统计图:折线图是用一个单位 ( http: / / www.21cnjy.com )表示一定的数量,根据数量的多少描出各点,然后把各点用线段依次连接起来.以折线的上升或下降来表示统计数量增减变化.折线图不但可以表示出数量的多少,而且能够清楚地表示出数量的增减变化情况.21*cnjy*com
2、92
【分析】
根据加权平均数的定义和计算公式计算可得.
【详解】
解:小丽的平均成绩是=92(分).
故答案为:92.
【点睛】
本题主要考查加权平均数,解题的关键是熟练掌握加权平均数的定义和计算公式.
3、小刘
【分析】
根据方差的意义即可求出答案.
【详解】
解:由于S小刘2<S小李2,且两人10次射击成绩的平均值相等,
∴两人中射击成绩比较稳定的是小刘,
故答案为:小刘
【点睛】
本题考查方差的意义,方差 ( http: / / www.21cnjy.com )是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定,熟练运用方差的意义是解题的关键.21世纪教育网版权所有
4、,
【分析】
先根据平均数的定义确定出的值,再根据方差的计算公式计算即可.
【详解】
解:数据 的平均数是,
,
,
这组数据的方差是:,
故答案为:2,.
【点睛】
此题考查了平均数和方差的定义,平均数是所有数据的和除以数据的个数.方差是一组数据中各数据与它们的平均数的差的平方的平均数.21·cn·jy·com
5、5.25
【分析】
根据加权平均数的计算公式,列出算式,计算即可求解.
【详解】
解:∵数据:6,4,10的权数分别是2,5,1,
∴这组数据的加权平均数是(6×2+4×5+10×1)÷(2+5+1)=5.25.
故答案为5.25.
【点睛】
本题考查的是加权平均数的求法,关键是根据加权平均数的计算公式列出算式.
三、解答题
1、(1)平均数是2.75分、中位数是3分,众数是3分;(2)1000人;(3)(加强体育锻炼)答案不唯一.www.21-cn-jy.com
【分析】
(1)根据平均数,众数及中位数的求法依次计算即可;
(2)利用总人数乘以合格人数占抽查总人数的比例即可;
(3)抓住健康第一,建议合理即可.
【详解】
解:(1)平均数为:;
抽查的120人中,成绩是3分出现的次数最多,共出现45次,因此众数是3分;
将这120人的得分从小到大排列处在60,61两个位置的分数都是3分,因此中位数是3分;
答:这组数据的平均数是2.75分,中位数是3分,众数是3分;
(2)估计本校学生体质健康测试成绩达到合格的人数为:
(人),
∴估计本校学生体质健康测试成绩达到合格的人数为1000人;
(3)加强体育锻炼(答案不唯一,合理即可).
【点睛】
题目主要考查从条形统计图获取信息,计算平均数,中位数,众数及利用部分估计整体,熟练掌握各个数据的计算方法是解题关键.21*cnjy*com
2、(1)见解析;(2)B;(3)1620人.
【分析】
(1)先由A组人数及其所占百分比求出总人数,总人数乘以B组对应百分比即可求出其人数,从而补全图形;
(2)根据中位数的定义求解;
(3)总人数乘以样本A、B组对应百分比之和即可.
【详解】
解:(1)因为被调查的总人数为40÷10%=400(人)
所以B组人数为400×35%=140(人),
补全图形如下,
( http: / / www.21cnjy.com / )
(2)因为一共有400个数据,其中位数是第200,201个数据的平均数,而这两个数据均落在B组,即本次调查测试成绩中的中位数落在B组,【出处:21教育名师】
故答案为:B;
(3)估计全校学生测试成绩为优秀的总人数为3600×(10%+35%)=1620(人)
答:估计全校学生测试成绩为优秀的总人数为1620人.
【点睛】
本题考查条形统计图与扇形统计图的综合应用、样本估计总体,难度一般,掌握相关知识是解题关键.
3、(1);(2)最高分116,最低分52;(3)83.25分;(4)没有达到,低15分
【分析】
(1)用小丽的数学成绩减去平均分即可得出小丽的离均差;
(2)①用班平均分加上离均差得出数学成绩,即可得出数学成绩的最高分与最低分;
②把这组同学的离均差相加除以8,再加上班平均分即可得出这组同学的平均分;
③用班平均分与组平均分作比较,作差即可得出答案.
【详解】
(1)小丽数学成绩的离均差为:;
(2)①这组同学数学成绩的最高分为:,
最低分为:;
②
(分),
∴这组同学数学成绩的平均分为83.25;
③∵,
∴该组数学成绩的平均分没有达到班平均分,
,
∴低了1.5分.
【点睛】
本题考查有理数的加减运算,掌握运算法则是解题的关键.
4、
(1)见解析
(2)4.5
(3)850
(4)见解析
【分析】
(1)根据5首的人数和圆心角的度数求出抽取的学生数量,再求出4首的人数即可;
(2)把数据从小到大排列,求中间两个数的平均数即可;
(3)求出大赛后一个月一周诗词诵背6首(含6首)以上的比例,乘以全校学生数即可;
(4)求出两次调查的平均数,比较大小即可.
(1)
解:由题意得抽查的这部分学生的数量为20÷=120(名),
大赛启动之初,一周诗词诵背数量为4首的人数为120×=45(名),补全统计图如图所示:
( http: / / www.21cnjy.com / )(2)
解:活动启动之初学生“一周诗词诵背数量”共抽 ( http: / / www.21cnjy.com )样调查了120人,处在第60位和第61位的数据分别为4首和5首,中位数为(4+5)÷2=4.5(首),【来源:21cnj*y.co*m】
故答案为:4.5.
(3)
解:大赛后一个月,一周诗词诵背6首(含6首)以上的的人数为(人),
答:估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数为850人.
(4)
解:活动启动之初的平均数为(首);
大赛后一个月的平均数为(首);
大赛后一个月学生 “一周诗词诵背数量” ( http: / / www.21cnjy.com )的平均数高于活动启动之初学生 “一周诗词诵背数量”的平均数,该校经典诗词诵背系列活动的效果非常好,提高了学生背诵诗词的能力.
【点睛】
本题考查条形统计图、扇形统计图以及平均数和中位数的计算公式,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.
5、(1),;(2)见解析;(3)1440名
【分析】
(1)样本容量=60÷0.2=300,90÷300=n;
(2)计算300×0.4=12,补图即可;
(3)用优秀率×2400,计算即可.
【详解】
解:(1)根据题意,得:60÷0.2=300(人),
∴90÷300=n=0.3;
故答案为:300, 0.3;
(2)∵300×0.4=120(人),
∴补图如下:
( http: / / www.21cnjy.com / )
(3)根据题意,优秀率为0.4+0.2,
∴(人),
答:该校2400名学生中竞赛成绩为“优秀”的有1440名.
【点睛】
本题考查了频数分布直方图,样本估计整体,正确理解样本容量,频数,频率之间的关系是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
九年级数学第二学期第二十八章统计初步定向测评
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内 ( http: / / www.21cnjy.com )相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。2·1·c·n·j·y
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、某校“安全知识”比赛有16名 ( http: / / www.21cnjy.com )同学参加,规定前8名的同学进入决赛.若某同学想知道自己能否晋级,不仅要了解自己的成绩,还需要了解16名参赛同学成绩的( )21·世纪*教育网
A.平均数 B.中位数 C.众数 D.方差
2、某校八年级人数相等的甲、乙、丙三个班,同时参加了一次数学测试,对成绩进行了统计分析,平均分都是72分,方差分别为,,,则成绩波动最小的班级( )
A.甲 B.乙 C.丙 D.无法确定
3、鞋厂生产不同号码的鞋,其中,生产数量最多的鞋号是调查不同年龄的人的鞋号所构成的数据的( )
A.平均数 B.众数 C.中位数 D.众数或中位数
4、下列调查中,其中适合采用抽样调查的是( )
A.调查某班50名同学的视力情况
B.为了解新型冠状病毒(SARS-CoV-2)确诊病人同一架飞机乘客的健康情况
C.为保证“神舟9号”成功发射,对其零部件进行检查
D.检测中卫市的空气质量
5、下列说法中,正确的是( )
A.若,,则
B.90′=1.5°
C.过六边形的每一个顶点有4条对角线
D.疫情防控期间,要掌握进入校园人员的体温是否正常,可采用抽样调查
6、如图,有100名学生 ( http: / / www.21cnjy.com )参加两次科技知识测试,条形图显示两次测试的分数分布情况.根据条形图提供的信息可知,两次测试最低分在第______ 次测试中,第____次测试较容易( )
( http: / / www.21cnjy.com / )
A.一,二 B.二,一 C.一,一 D.二,二
7、下列采用的调查方式中,不合适的是
A.了解一批灯泡的使用寿命,采用普查
B.了解神舟十二号零部件的质量情况,采用普查
C.了解单县中学生睡眠时间,采用抽样调查
D.了解中央电视台《开学第一课》的收视率,采用抽样调查
8、下列调查中,调查方式选择不合理的是( )
A.为了了解新型炮弹的杀伤半径,选择抽样调查
B.为了了解某河流的水质情况,选择普查
C.为了了解神舟飞船的设备零件的质量情况,选择普查
D.为了了解一批袋装食品是否含有防腐剂,选择抽样调查
9、一组数据的最大值为105,最小值为23,若确定组距为9,则分成的组数为( )
A.11 B.10 C.9 D.8
10、小明抛一枚硬币100次,其中有60次正面朝上,则反面朝上的频率是( )
A.0.6 B.6 C.0.4 D.4
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、如图是某同学6次数学测验成绩的折线统计图,则该同学这6次成绩最高分与最低分的差是_________分.21教育名师原创作品
( http: / / www.21cnjy.com / )
2、小丽的笔试成绩为90分,面试成绩为95分,若笔试成绩、面试成绩按6:4计算平均成绩,则小丽的平均成绩是 _______分.
3、小刘和小李参加射击训练,各射击10次的平均成绩相同,如果他们射击成绩的方差分别是,,那么两人中射击成绩比较稳定的是_________.
4、已知一组数据,,,它们的平均数是,则______,这一组数据的方差为______.
5、一组数据:6,4,10的权数分别是2,5,1,则这组数据的加权平均数是______.
三、解答题(5小题,每小题10分,共计50分)
1、本校将学生体质健康测试成绩分为A,B,C,D四个等级,依次记为4分,3分,2分,1分.为了解学生整体体质健康状况,拟抽样进行统计分析.
(1)现将随机抽取的测试成绩整理并绘制成如图统计图,请求出这组数据的平均数、中位数和众数;
本校部分学生体质健康测试成绩统计图
( http: / / www.21cnjy.com / )
(2)本校规定达到3分才算合格. 已知本校共有学生1600人,根据以上数据估计本校学生体质健康测试成绩达到合格的人数;
(3)为了更好贯彻落实健康第一的指导思想,请你根据以上数据对本校体育老师提出一条合理的建议.
2、西安市某中学为了搞好“创建全 ( http: / / www.21cnjy.com )国文明城市”的宣传活动,对本校部分学生(随机抽查)进行了一次相关知识了解程度的调查测试(成绩分为A、B、C、D、E五个组,X表示测试成绩)通过对测试成绩的分析,得到如图所示的两幅不完整的统计图.请你根据图中提供的信息解答以下问题:
( http: / / www.21cnjy.com / )
(1)将条形统计图补充完整;
(2)本次调查测试成绩中的中位数落在______组内;
(3)若测试成绩在80分以上(含80分)为优秀,有学生3600人,请你根据样本数据估计全校学生测试成绩为优秀的总人数.21cnjy.com
3、至善中学七年一班期中考试数学成绩平均分 ( http: / / www.21cnjy.com )为84.75,该班小明的数学成绩为92分,把92与84.75的差叫做小明数学成绩的离均差,即小明数学成绩的离均差为+7.25.2-1-c-n-j-y
(1)该班小丽的数学成绩为82分,求小丽数学成绩的离均差.
(2)已知该班第一组8名同学数学成绩的离均差分别为:
+10.25,﹣8.75,+31.25,+15.25,﹣3.75,﹣12.75,﹣10.75,﹣32.75.
①求这组同学数学成绩的最高分和最低分;
②求这组同学数学成绩的平均分;
③若该组数学成绩最低的同学达到及格的72分,则该组数学成绩的平均分是否达到或超过班平均分?超过或低于多少分?
4、为积极响应“弘扬传统文化 ( http: / / www.21cnjy.com )”的号召,某校倡导全校1200名学生进行经典诗词诵背活动,并在活动之后举办经典诗词大赛,为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取部分学生调查“一周诗词诵背数量”.根据调查结果绘制成的统计图(部分)如下图所示:
( http: / / www.21cnjy.com / )
大赛结束后一个月,再次抽查这部分学生“一周诗词诵背数量”,绘制成统计表:
一周诗词诵背数量 3首 4首 5首 6首 7首 8首
人数 10 10 15 40 25 20
请根据调查的信息分析:
(1)补全频数分布直方图.
(2)活动启动之初学生“一周诗词诵背数量”的中位数为______首.
(3)估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数.
(4)选择适当的统计量,从某一个角度分析两次调查的相关数据,评价该校经典诗词诵背系列活动的效果.
5、为深入开展青少年毒品预防教育工 ( http: / / www.21cnjy.com )作,增强学生禁毒意识,某校联合禁毒办组织开展了“2021青少年禁毒知识竞赛”活动,并随即抽查了部分同学的成绩,整理并制作成图表如下:
( http: / / www.21cnjy.com / ) ( http: / / www.21cnjy.com / )
根据以上图表提供的信息,回答下列问题:
(1)抽查的人数为______人,______;
(2)请补全频数分布直方图;
(3)若成绩在80分以上(包括80分)为“优秀”,请你估计该校2400名学生中竞赛成绩是“优秀”的有多少名?www-2-1-cnjy-com
-参考答案-
一、单选题
1、B
【分析】
由中位数的概念,即最中间一个或两个数据的平均 ( http: / / www.21cnjy.com )数;可知16人成绩的中位数是第8名和第9名的成绩.根据题意可得:参赛选手要想知道自己是否能进入前8名,只需要了解自己的成绩以及全部成绩的中位数,比较即可.
【详解】
解:由于16个人中,第8和 ( http: / / www.21cnjy.com )第9名的成绩的平均数是中位数,故同学知道了自己的分数后,想知道自己能否进入决赛,还需知道这16位同学的成绩的中位数.
故选:B.
【点睛】
此题主要考查统计的有关知识,主要包括 ( http: / / www.21cnjy.com )平均数、中位数、众数的意义.反映数据集中程度的统计量有平均数、中位数、众数等,各有局限性,因此要对统计量进行合理的选择和恰当的运用.
2、C
【分析】
根据方差的意义可作出判断.方差是用 ( http: / / www.21cnjy.com )来衡量一组数据波动大小的量,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
【详解】
解:∵,,,
∴,
∴成绩波动最小的班级是:丙班.
故选:C.
【点睛】
此题主要考查了方差的意义,正确理解方差的意义是解题关键.
3、B
【分析】
由鞋厂关心的数据,即大众买的最多的鞋号,也就是出现次数最多的数据,从而可得所构成的数据是众数.
【详解】
解:生产数量最多的鞋号是调查不同年龄的人的鞋号所构成的数据的众数,
故选B
【点睛】
本题考查的是众数的含义及众数表示的意义,理解众数的含义及在生活中的应用是解本题的关键.
4、D
【分析】
抽样调查是通过对样本调查来估计总体特征,其调查结果是近似的;而全面调查得到的结果比较准确;根据对调查结果的要求对选项进行判断.
【详解】
A调查某班50名同学的视力情况,人数较少,应采用全面调查,故不符合要求;
B为了解新型冠状病毒确诊病人同一架飞机乘客的健康状况,意义重大,应采用全面调查,故不符合要求;
C为保证“神州9号”成功发射,对零部件进行检查,意义重大,应采用全面调查,故不符合要求;
D检查中卫市的空气质量,应采用抽样调查,故符合要求;
故选D.
【点睛】
本题考察了抽样调查与全面调查.解题的关键与难点在于理清对调查结果的要求.
5、B
【分析】
由等式的基本性质可判断A,由 可判断B,由过边形的一个顶点可作条对角线可判断C,由全面调查与抽样调查的含义可判断D,从而可得答案.【版权所有:21教育】
【详解】
解:若,则故A不符合题意;
90′=故B符合题意;
过六边形的每一个顶点有3条对角线,故C不符合题意;
疫情防控期间,要掌握进入校园人员的体温是否正常,事关重大,一定采用全面调查,故D不符合题意;
故选:B.
【点睛】
本题考查的是等式的基本性质,角度的换算,多边形的对角线问题,全面调查与抽样调查的含义,掌握以上基础知识是解本题的关键.
6、A
【分析】
根据条形统计图,发现最低分显然在第一次测验中;因为第二次测验的高分人数较多,所以第二次测验较容易.
【详解】
解:根据条形统计图,发现最低分在第一次测验中;因为第二次测验的高分人数较多,所以第二次测验较容易.
故选A.
【点睛】
条形统计图能清楚地表示出每个项目的数据,能够根据条形统计图读懂两者分别表示的意义是关键.
7、A
【分析】
根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似解答即可.21教育网
【详解】
解:A、了解一批灯泡的使用寿命,采用抽样调查,本选项说法不合适,符合题意;
、了解神舟十二号零部件的质量情况,采用普查,本选项说法合适,不符合题意;
、了解单县中学生睡眠时间,采用抽样调查,本选项说法合适,不符合题意;
、了解中央电视台《开学第一课》的收视率,采用抽样调查,本选项说法合适,不符合题意;
故选:A.
【点睛】
本题考查的是抽样调查和全面调查,选择普查还 ( http: / / www.21cnjy.com )是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.【来源:21·世纪·教育·网】
8、B
【分析】
根据调查的不同目的来选择全面调查或抽样调查,再判断四个选项即可.
【详解】
解:A选项,C选项,D选项选择调查方式合理,故A选项,C选项,D选项不符合题意.
B选项,为了了解某河流的水质情况,选择普查耗费人力,物力和时间较多,而选择抽样调查更加节约,且和普查的结果相差不大,故B选项符合题意.
故选:B.
【点睛】
本题考查全面调查和抽样调查,对于具有破坏性 ( http: / / www.21cnjy.com )的调查、无法进行全面调查、全面调查的意义或价值不大时,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用全面调查.
9、B
【分析】
极差除以组距,大于或等于该值的最小整数即为组数.
【详解】
解:,
分10组.
故选:B.
【点睛】
本题考查了组距的划分,一般分为组最科学.
10、C
【分析】
先求出反面朝上的频数,然后根据频率=频数÷总数求解即可
【详解】
解:∵小明抛一枚硬币100次,其中有60次正面朝上,
∴小明抛一枚硬币100次,其中有40次反面朝上,
∴反面朝上的频率=40÷100=0.4,
故选C.
【点睛】
本题主要考查了根据频数求频率,解题的关键在于能够熟练掌握频率=频数÷总数.
二、填空题
1、25
【分析】
先从统计图中读出这6次成绩的最高分与最低分,然后相减即可.
【详解】
解:根据折线统计图可知,这6次成绩分别是(单位:分):
65,75,60,80,70,85
其中,最高分是85分,最低分是60分,
所以,最高分与最低分的差是85-60=25(分).
故答案为:25.
【点睛】
本题考查了折线统计图:折线图是用一个单位 ( http: / / www.21cnjy.com )表示一定的数量,根据数量的多少描出各点,然后把各点用线段依次连接起来.以折线的上升或下降来表示统计数量增减变化.折线图不但可以表示出数量的多少,而且能够清楚地表示出数量的增减变化情况.21*cnjy*com
2、92
【分析】
根据加权平均数的定义和计算公式计算可得.
【详解】
解:小丽的平均成绩是=92(分).
故答案为:92.
【点睛】
本题主要考查加权平均数,解题的关键是熟练掌握加权平均数的定义和计算公式.
3、小刘
【分析】
根据方差的意义即可求出答案.
【详解】
解:由于S小刘2<S小李2,且两人10次射击成绩的平均值相等,
∴两人中射击成绩比较稳定的是小刘,
故答案为:小刘
【点睛】
本题考查方差的意义,方差 ( http: / / www.21cnjy.com )是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定,熟练运用方差的意义是解题的关键.21世纪教育网版权所有
4、,
【分析】
先根据平均数的定义确定出的值,再根据方差的计算公式计算即可.
【详解】
解:数据 的平均数是,
,
,
这组数据的方差是:,
故答案为:2,.
【点睛】
此题考查了平均数和方差的定义,平均数是所有数据的和除以数据的个数.方差是一组数据中各数据与它们的平均数的差的平方的平均数.21·cn·jy·com
5、5.25
【分析】
根据加权平均数的计算公式,列出算式,计算即可求解.
【详解】
解:∵数据:6,4,10的权数分别是2,5,1,
∴这组数据的加权平均数是(6×2+4×5+10×1)÷(2+5+1)=5.25.
故答案为5.25.
【点睛】
本题考查的是加权平均数的求法,关键是根据加权平均数的计算公式列出算式.
三、解答题
1、(1)平均数是2.75分、中位数是3分,众数是3分;(2)1000人;(3)(加强体育锻炼)答案不唯一.www.21-cn-jy.com
【分析】
(1)根据平均数,众数及中位数的求法依次计算即可;
(2)利用总人数乘以合格人数占抽查总人数的比例即可;
(3)抓住健康第一,建议合理即可.
【详解】
解:(1)平均数为:;
抽查的120人中,成绩是3分出现的次数最多,共出现45次,因此众数是3分;
将这120人的得分从小到大排列处在60,61两个位置的分数都是3分,因此中位数是3分;
答:这组数据的平均数是2.75分,中位数是3分,众数是3分;
(2)估计本校学生体质健康测试成绩达到合格的人数为:
(人),
∴估计本校学生体质健康测试成绩达到合格的人数为1000人;
(3)加强体育锻炼(答案不唯一,合理即可).
【点睛】
题目主要考查从条形统计图获取信息,计算平均数,中位数,众数及利用部分估计整体,熟练掌握各个数据的计算方法是解题关键.21*cnjy*com
2、(1)见解析;(2)B;(3)1620人.
【分析】
(1)先由A组人数及其所占百分比求出总人数,总人数乘以B组对应百分比即可求出其人数,从而补全图形;
(2)根据中位数的定义求解;
(3)总人数乘以样本A、B组对应百分比之和即可.
【详解】
解:(1)因为被调查的总人数为40÷10%=400(人)
所以B组人数为400×35%=140(人),
补全图形如下,
( http: / / www.21cnjy.com / )
(2)因为一共有400个数据,其中位数是第200,201个数据的平均数,而这两个数据均落在B组,即本次调查测试成绩中的中位数落在B组,【出处:21教育名师】
故答案为:B;
(3)估计全校学生测试成绩为优秀的总人数为3600×(10%+35%)=1620(人)
答:估计全校学生测试成绩为优秀的总人数为1620人.
【点睛】
本题考查条形统计图与扇形统计图的综合应用、样本估计总体,难度一般,掌握相关知识是解题关键.
3、(1);(2)最高分116,最低分52;(3)83.25分;(4)没有达到,低15分
【分析】
(1)用小丽的数学成绩减去平均分即可得出小丽的离均差;
(2)①用班平均分加上离均差得出数学成绩,即可得出数学成绩的最高分与最低分;
②把这组同学的离均差相加除以8,再加上班平均分即可得出这组同学的平均分;
③用班平均分与组平均分作比较,作差即可得出答案.
【详解】
(1)小丽数学成绩的离均差为:;
(2)①这组同学数学成绩的最高分为:,
最低分为:;
②
(分),
∴这组同学数学成绩的平均分为83.25;
③∵,
∴该组数学成绩的平均分没有达到班平均分,
,
∴低了1.5分.
【点睛】
本题考查有理数的加减运算,掌握运算法则是解题的关键.
4、
(1)见解析
(2)4.5
(3)850
(4)见解析
【分析】
(1)根据5首的人数和圆心角的度数求出抽取的学生数量,再求出4首的人数即可;
(2)把数据从小到大排列,求中间两个数的平均数即可;
(3)求出大赛后一个月一周诗词诵背6首(含6首)以上的比例,乘以全校学生数即可;
(4)求出两次调查的平均数,比较大小即可.
(1)
解:由题意得抽查的这部分学生的数量为20÷=120(名),
大赛启动之初,一周诗词诵背数量为4首的人数为120×=45(名),补全统计图如图所示:
( http: / / www.21cnjy.com / )(2)
解:活动启动之初学生“一周诗词诵背数量”共抽 ( http: / / www.21cnjy.com )样调查了120人,处在第60位和第61位的数据分别为4首和5首,中位数为(4+5)÷2=4.5(首),【来源:21cnj*y.co*m】
故答案为:4.5.
(3)
解:大赛后一个月,一周诗词诵背6首(含6首)以上的的人数为(人),
答:估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数为850人.
(4)
解:活动启动之初的平均数为(首);
大赛后一个月的平均数为(首);
大赛后一个月学生 “一周诗词诵背数量” ( http: / / www.21cnjy.com )的平均数高于活动启动之初学生 “一周诗词诵背数量”的平均数,该校经典诗词诵背系列活动的效果非常好,提高了学生背诵诗词的能力.
【点睛】
本题考查条形统计图、扇形统计图以及平均数和中位数的计算公式,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.
5、(1),;(2)见解析;(3)1440名
【分析】
(1)样本容量=60÷0.2=300,90÷300=n;
(2)计算300×0.4=12,补图即可;
(3)用优秀率×2400,计算即可.
【详解】
解:(1)根据题意,得:60÷0.2=300(人),
∴90÷300=n=0.3;
故答案为:300, 0.3;
(2)∵300×0.4=120(人),
∴补图如下:
( http: / / www.21cnjy.com / )
(3)根据题意,优秀率为0.4+0.2,
∴(人),
答:该校2400名学生中竞赛成绩为“优秀”的有1440名.
【点睛】
本题考查了频数分布直方图,样本估计整体,正确理解样本容量,频数,频率之间的关系是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
