【最新强化训练】沪教版(上海)九下 第二十八章统计初步专题攻克试题(含答案解析)
文档属性
| 名称 | 【最新强化训练】沪教版(上海)九下 第二十八章统计初步专题攻克试题(含答案解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-24 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
九年级数学第二学期第二十八章统计初步专题攻克
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内 ( http: / / www.21cnjy.com )相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。2·1·c·n·j·y
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、甲、乙、丙、丁四名同学进行立定跳远测试,每人10次立定跳远成绩的平均数都是2.25米,方差分别是,,,,则这四名同学立定跳远成绩最稳定的是( ).
A.甲 B.乙 C.丙 D.丁
2、下列命题正确的是( )
A.数轴上的每一个点都表示一个有理数
B.甲、乙两人五次考试平均成绩相同,且,,则乙的成绩更稳定
C.三角形的一个外角大于任意一个内角
D.在平面直角坐标系中,点与点关于x轴对称
3、下列说法中,正确的是( )
A.若,,则
B.90′=1.5°
C.过六边形的每一个顶点有4条对角线
D.疫情防控期间,要掌握进入校园人员的体温是否正常,可采用抽样调查
4、某县为了传承中华优秀传统文化,组织了一 ( http: / / www.21cnjy.com )次全县600名学生参加的“中华经典诵读”大赛.为了解本次大赛的选手成绩,随机抽取了其中50名选手的成绩进行统计分析.在这个问题中,下列说法中正确的是( )
A.这600名学生的“中华经典诵读”大赛成绩的全体是总体
B.50名学生是总体的一个样本
C.每个学生是个体
D.样本容量是50名
5、下列调查中,适合采用全面调查的是( )
A.了解一批电灯泡的使用寿命 B.调查榆林市中学生的视力情况
C.了解榆林市居民节约用水的情况 D.调查“天问一号”火星探测器零部件的的质量
6、根据下面的两幅统计图,你认为哪种说法不合理( )
( http: / / www.21cnjy.com / )
A.六(2)班女生人数一定比六(1)班多 B.两个班女生人数可能同样多
C.六(2)班女生人数可能比六(1)班多 D.六(2)班女生人数一定比男生多
7、某中学规定学生的学期 ( http: / / www.21cnjy.com )体育成绩满分为100分,其中课外体育占20%,期中考试成绩占30%,期末考试成绩占50%.小彤的三项成绩(百分制)依次为95,90,88,则小彤这学期的体育成绩为( )
A.89 B.90 C.91 D.92
8、为了了解2017年我县九年级6023名学生学业水平考试的数学成绩,从中随机抽取了200名学生的数学成绩,下列说法正确的是( )【出处:21教育名师】
A.2017年我县九年级学生是总体 B.每一名九年级学生是个体
C.200名九年级学生是总体的一个样本 D.样本容量是200
9、某校男子足球队的年龄分布如图条形图所示,则这些队员年龄的众数是( )
( http: / / www.21cnjy.com / )
A.8 B.13 C.14 D.15
10、甲、乙、丙、丁四位同学都参加了5次数学模拟测试,每个人这5次成绩的平均数都是92分,方差分别是,,,,则这5次测试成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、为庆祝中国共产党建党一百周年,某 ( http: / / www.21cnjy.com )单位党支部开展“学史明理,学史增信,学史崇德,学史力行”读书活动,学习小组抽取了七名党员5天的学史的时间(单位:h)分别为:4,3,3,5,6,5,5,这组数据的众数是________.
2、新兴农场果农随机从甲、乙、丙三个品种的枇杷树中各选10棵,每棵产量的平均数(单位:千克)及方差(单位:千克)如下表所示,他准备从这三个品种中选出一种产量既高又稳定的枇杷树进行种植,则应选的品种是______.
甲 乙 丙
44 44 42
1.7 1.5 1.7
3、对于两组数据来说,可 ( http: / / www.21cnjy.com )从平均数和方差两个方面进行比较,平均数反映一组数据的______,方差则反映一组数据在平均数左右的______,因此从平均数看或从方差看,各有长处.
4、小丽的笔试成绩为90分,面试成绩为95分,若笔试成绩、面试成绩按6:4计算平均成绩,则小丽的平均成绩是 _______分.
5、圆周率π≈3.141592653589793,数字5出现的频数是____.
三、解答题(5小题,每小题10分,共计50分)
1、为促进学生健康成长,帮助 ( http: / / www.21cnjy.com )家长解决按时接送学生困难的问题,认真落实全国教育大会精神,某校结合自身情况,在开展中学生课后服务工作方面做了全面规划,并且落到实处.在不加重学生课业负担的前提下,学校在托管时间内组织学生进行自主阅读、体育、艺术、及其他一些有益身心健康的活动,学生根据自己的喜好,自主选择.学校随机抽取了部分学生进行调查(抽取的学生都选择了一种自己喜爱的活动),下面是根据调查情况,得到的两幅不完整的统计图,请结合图中信息解答下列问题:21*cnjy*com
( http: / / www.21cnjy.com / )
(1)求出本次调查中,随机抽取的学生人数;
(2)补全条形统计图,并求出“其他”所对应的圆心角的度数;
(3)若该校学生总人数为840人,估计选择阅读的学生有多少人?
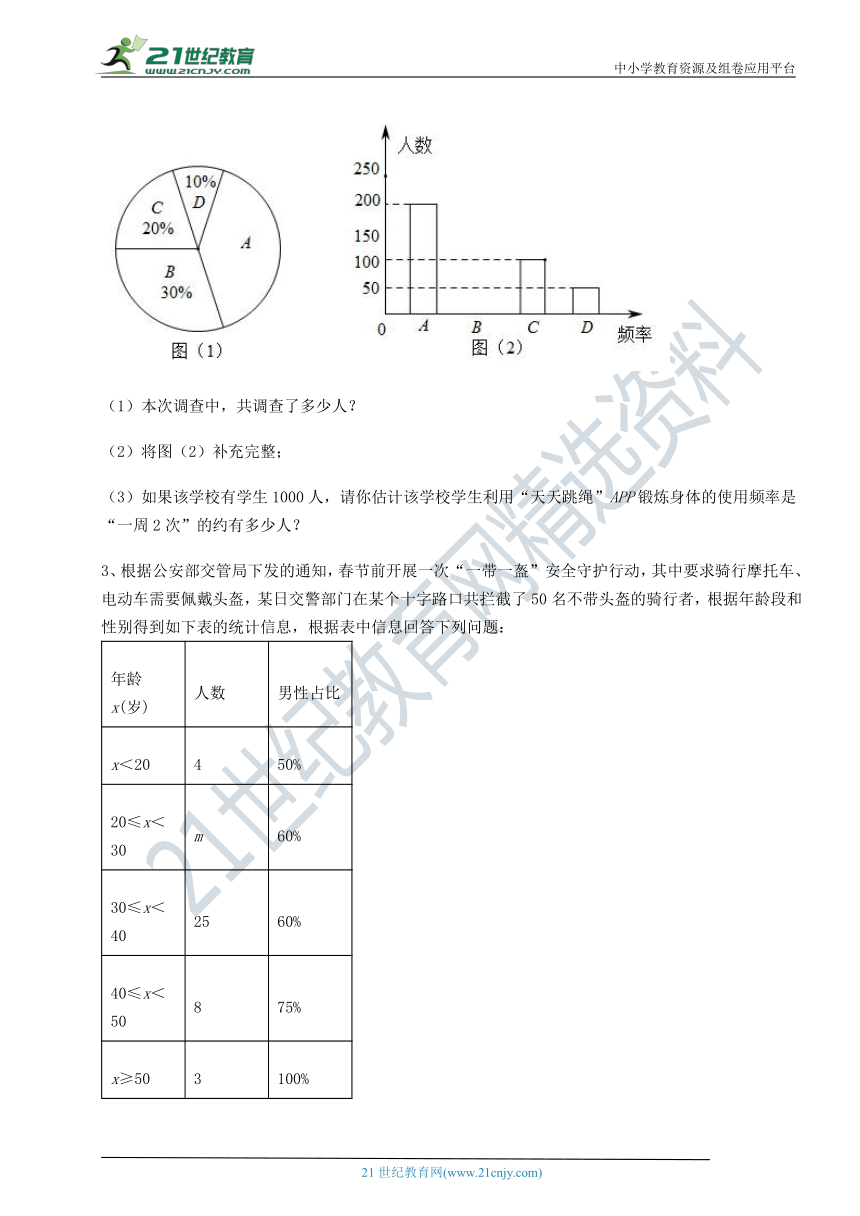
2、某学校为了调查学生利用“天天跳绳” ( http: / / www.21cnjy.com )APP锻炼身体的使用频率,随机抽取了部分学生,利用调查问卷进行抽样调查:用“A”表示“一周5次”,“B”表示“一周4次”,“C”表示“一周3次”,“D”表示“一周2次”(必须选且只选一项),如图是工作人员根据问卷调查统计资料绘制的两幅不完整的统计图,请你根据统计图提供的信息回答以下问题:
( http: / / www.21cnjy.com / )
(1)本次调查中,共调查了多少人?
(2)将图(2)补充完整;
(3)如果该学校有学生1000人,请你估计该学校学生利用“天天跳绳”APP锻炼身体的使用频率是“一周2次”的约有多少人?
3、根据公安部交管局下发的通知,春 ( http: / / www.21cnjy.com )节前开展一次“一带一盔”安全守护行动,其中要求骑行摩托车、电动车需要佩戴头盔,某日交警部门在某个十字路口共拦截了50名不带头盔的骑行者,根据年龄段和性别得到如下表的统计信息,根据表中信息回答下列问题:
年龄x(岁) 人数 男性占比
x<20 4 50%
20≤x<30 m 60%
30≤x<40 25 60%
40≤x<50 8 75%
x≥50 3 100%
(1)统计表中m的值为 ;
(2)若要按照表格中各年龄段的人数来绘制扇形统计图,则年龄在“30≤x<40”部分所对应扇形的圆心角的度数为 ;
(3)若从年龄在“x<20”的4人中随机抽取2人参加交通安全知识学习,请用列表或画树状图的方法,求恰好抽到1名男性和1名女性的概率.
4、为了了解我校学生对英语单词掌握的情况 ( http: / / www.21cnjy.com ),现对全校学生进行英语百词测试,为了了解测试结果,随机抽取部分学生的成绩进行分析,现将成绩分为三个等级:不合格、一般、优秀,并绘制成如下两幅统计图(不完整).请根据图中所给的信息解答下列问题:
( http: / / www.21cnjy.com / )
(1)本次随机抽取的人数是 人 ,并将以上两幅统计图补充完整;
(2)若“一般”和“优秀”均被视为达标成绩,则我校被抽取的学生中有 人达标;
(3)若我校学生有1800人,请你估计此次测试中,全校达标的学生有多少人?
5、为深入开展青少年毒品预防教育工 ( http: / / www.21cnjy.com )作,增强学生禁毒意识,某校联合禁毒办组织开展了“2021青少年禁毒知识竞赛”活动,并随即抽查了部分同学的成绩,整理并制作成图表如下:
( http: / / www.21cnjy.com / ) ( http: / / www.21cnjy.com / )
根据以上图表提供的信息,回答下列问题:
(1)抽查的人数为______人,______;
(2)请补全频数分布直方图;
(3)若成绩在80分以上(包括80分)为“优秀”,请你估计该校2400名学生中竞赛成绩是“优秀”的有多少名?21*cnjy*com
-参考答案-
一、单选题
1、D
【分析】
平均数相同,方差值越小越稳定,比较四名同学方差值的大小即可.
【详解】
解:∵
∴丁同学的成绩最稳定
故选D.
【点睛】
本题考查了方差.解题的关键在于理解方差值越小的数据越稳定.
2、D
【分析】
根据数轴上的点与实数一一对应即可判断A;根据平均数相同的情形下,方差越小,成绩越稳定即可判断B;根据三角形的外角与内角的关系即可判断C;根据关于轴对称的点的坐标特征即可判断D
【详解】
A. 数轴上的每一个点都表示一个实数,故该选项不正确,不符合题意;
B. 甲、乙两人五次考试平均成绩相同,且,,则甲的成绩更稳定,故该选项不正确,不符合题意;
C. 三角形的一个外角不一定大于任意一个内角,故该选项不正确,不符合题意;
D. 在平面直角坐标系中,点与点关于x轴对称,故该选项正确,符合题意;
故选D
【点睛】
本题考查了实数与数轴,方差的意义,三角形的外角的性质,关于轴对称的点的坐标特征,掌握以上知识是解题的关键.21·cn·jy·com
3、B
【分析】
由等式的基本性质可判断A,由 可判断B,由过边形的一个顶点可作条对角线可判断C,由全面调查与抽样调查的含义可判断D,从而可得答案.
【详解】
解:若,则故A不符合题意;
90′=故B符合题意;
过六边形的每一个顶点有3条对角线,故C不符合题意;
疫情防控期间,要掌握进入校园人员的体温是否正常,事关重大,一定采用全面调查,故D不符合题意;
故选:B.
【点睛】
本题考查的是等式的基本性质,角度的换算,多边形的对角线问题,全面调查与抽样调查的含义,掌握以上基础知识是解本题的关键.21教育网
4、A
【分析】
根据总体的定义:表示考察的全体对象;样本 ( http: / / www.21cnjy.com )的定义:按照一定的抽样规则从总体中取出的一部分个体,样本中个体的数目称为样本容量;个体的定义:总体中每个成员成为个体,进行逐一判断即可.
【详解】
解:A、这600名学生的“中华经典诵读”大赛成绩的全体是总体,故本选项正确,符合题意;
B、50名学生的成绩是总体的一个样本,故本选项错误,不符合题意;
C、每个学生的成绩是个体,故本选项错误,不符合题意;
D、样本容量是50,故本选项错误,不符合题意;
故选A.
【点睛】
本题主要考查了样本,总体,个体和样本容量的定义,解题的关键在于熟知相关定义.
5、D
【分析】
由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似,再逐一分析即可.21cnjy.com
【详解】
解:A.了解一批电灯泡的使用寿命,具有破坏性,适合抽样调查,不符合题意;
B.调查榆林市中学生的视力情况,适合抽样调查,不符合题意;
C.了解榆林市居民节约用水的情况,适合抽样调查,不符合题意;
D.调查“天问一号”火星探测器零部件的的质量,必需采用全面调查,符合题意;
故选:D.
【点睛】
本题考查了抽样调查和全面 ( http: / / www.21cnjy.com )调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.【版权所有:21教育】
6、A
【分析】
根据两个扇形统计图,只能得到两个班级男女生比例的大小,无法确定男生和女生的具体人数,由此即可得.
【详解】
解:∵两个班的人数不知道,
∴无法确定每个班的男生和女生的具体人数,
∴六(2)班女生人数一定比六(1)班多不合理,
故选:A.
【点睛】
题目主要考查从扇形统计图获取信息,理解题意,掌握扇形统计图表示的意义是解题关键.
7、B
【分析】
根据加权平均数的计算公式列出算式,再进行计算即可.
【详解】
解:根据题意得:
95×20%+90×30%+88×50%=90(分).
即小彤这学期的体育成绩为90分.
故选:B.
【点睛】
此题考查了加权平均数,掌握加权平均数的计算公式是本题的关键,是一道常考题.
8、D
【分析】
总体是指考查的对象的全体,个体是总体中的每 ( http: / / www.21cnjy.com )一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.根据总体、个体、样本、样本容量的定义,做出判断.
【详解】
解: 2017年我县九年级学生的数学成绩是总体,故A不符合题意;
每一名九年级学生的数学成绩是个体,故B不符合题意;
200名九年级学生的数学成绩是总体的一个样本,故C不符合题意;
样本容量是200,故D符合题意;
故选D
【点睛】
考查了总体、个体、样本、样 ( http: / / www.21cnjy.com )本容量,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.2-1-c-n-j-y
9、C
【分析】
根据众数的定义:一组数据中出现次数最多的那个数,称为这组数据的众数,据此结合条形图可得答案.
【详解】
解:由条形统计图知14岁出现的次数最多,
所以这些队员年龄的众数为14岁,
故选C.
【点睛】
本题考查了众数的定义及条形统计图的知识,解题的关键是能够读懂条形统计图及了解众数的定义.
10、D
【分析】
根据方差越大,则数据的离散程度越大,稳定性也越小;反之,则数据的离散程度越小,稳定性越好,进而分析即可.21·世纪*教育网
【详解】
解:∵,,,,
∴S丁2<S丙2<S乙2<S甲2,
∴成绩最稳定的是丁.
故选:D.
【点睛】
本题考查了方差的意义,方差是用来衡 ( http: / / www.21cnjy.com )量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,数据越稳定.
二、填空题
1、5h
【分析】
根据众数的意义(出现次数最多的数据是众数)可得答案.
【详解】
解:这组数据中出现次数最多的是5h,共出现3次,
所以众数是5h,
故答案为:5h.
【点睛】
本题考查众数,理解众数的意义是解决问题的关键.
2、乙
【分析】
先比较平均数得到甲和乙产量较高,然后比较方差得到乙比较稳定.
【详解】
解:因为甲、乙的平均数比丙大,所以甲、乙的产量较高,
又乙的方差比甲小,所以乙的产量比较稳定,
即从这三个品种中选出一种产量既高又稳定的枇杷树进行种植,则应选的品种是乙;
故答案为:乙.
【点睛】
本题考查了方差:一组数据中各数据与它 ( http: / / www.21cnjy.com )们的平均数的差的平方的平均数,叫做这组数据的方差.方差是反映一组数据的波动大小的一个量.方差越大,则与平均值的离散程度越大,稳定性也越差;反之,则它与其平均值的离散程度越小,稳定性越好.也考查了平均数.www.21-cn-jy.com
3、一般水平 波动大小
【分析】
根据平均数和方差的意义进行回答即可.
【详解】
解:平均数反映一组数据的一般水平,方差则反映一组数据在平均数左右的波动大小,
故答案为:一般水平;波动大小
【点睛】
本题考查了平均数和方差的区别,熟练掌握平均数和方差的意义是解答本题的关键.
4、92
【分析】
根据加权平均数的定义和计算公式计算可得.
【详解】
解:小丽的平均成绩是=92(分).
故答案为:92.
【点睛】
本题主要考查加权平均数,解题的关键是熟练掌握加权平均数的定义和计算公式.
5、3
【分析】
从数5出现的次数即可得出答案.
【详解】
在中,5出现了3次,
∴数字5出现的频数是3.
故答案为:3.
【点睛】
本题考查频数的定义:一组数据中,某数据出现的次数,掌握频数的定义是解题的关键.
三、解答题
1、(1)120人;(2)见解析,36°;(3)126人
【分析】
(1)从条形图选择体育的人数÷从扇形图中体育所占百分比计算即可;
(2)从调查总人数减去阅读,体育和其它得出艺术人数,补画条形图,再求出其它12人除以120得出所占百分比,再乘以360°即可;【来源:21·世纪·教育·网】
(3)先计算样本中选择阅读所占样本的百分比,再用样本中所含百分比乘以总数估计总体中的含量即可.
【详解】
解:(1)本次调查中从条形图得出选择体育有54人,从扇形统计图中体育所占百分比为45%,
本次调查人数为:(人);
(2)∵艺术:(人),
∴补全的条形统计图如下图所示:
( http: / / www.21cnjy.com / )
“其他”所对应的圆心角度数为;
(3)样本中选择阅读的人数为18人,占样本的百分比为,
该校学生总人数为840人,估计选择阅读的学生有:(人),
∴选择“阅读”的学生大约有126人.
【点睛】
本题考查从条形图和扇形统计图获取信 ( http: / / www.21cnjy.com )息和处理信息能力,样本容量,补画条形图,扇形圆心角,用样本的百分比含量估计总体中的数量,掌握以上知识是解题关键.www-2-1-cnjy-com
2、(1)人;(2)补全图形见解析;(3)人
【分析】
(1)由C组有100人,占比列式计算后可得答案;
(2)先求解B组人数,再补全图形即可;
(3)由总人数1000乘以D组“一周2次”的占比即可得到答案.
【详解】
解:(1)由C组有100人,占比 可得:
本次调查中,共调查人.
(2)B组人数有人,
补全图形如下:
( http: / / www.21cnjy.com / )
(3)该学校有学生1000人,该学校学生利用“天天跳绳”APP锻炼身体的使用频率是“一周2次”的约有:人.【来源:21cnj*y.co*m】
【点睛】
本题考查的是从扇形图与条形图中获取信息,补全条形统计图,利用样本估计总体,理解扇形图与条形图中关联信息是解本题的关键.21教育名师原创作品
3、
(1)10
(2)180°
(3)见解析,
【分析】
(1)根据总数减去表格中其他数据即可求解;
(2)根据年龄在“30≤x<40”的人数占总人数的比例乘以360°即可求解;
(3)用列表法求概率即可.
(1)
故答案为:10
(2)
故答案为:
(3)
设两名男性用表示,两名女性用表示,根据题意,列表如下,
由上表可知,共有12种等可能的结果,符合条件的结果有8种,
故P(恰好抽到1名男性和1名女性)=
【点睛】
本题考查了求扇形统计图的圆心角的度数,求频数,根据列表法求概率,理解题意,掌握以上知识是解题的关键.
4、(1)120,统计图补充见详解;(2)96;(3)1440人.
【分析】
(1)用不合格人数24除以占比20%即可求出 ( http: / / www.21cnjy.com )抽取人数未120人,用1减去优秀占比和不合格占比即可求出一般占比,用120乘以优秀占比50%即可求出优秀人数,再补充两幅统计图即可;
(2)用120乘以优秀与一般占比之和,即可求出抽取学生中达标人数;
(3)用1800乘以优秀与一般占比之和,即可估算出全校达标学生数.
【详解】
解:(1)24÷20%=120(人),1-50%-20%=30%,120×50%=60(人),
故答案为:120,
统计图补充如图:
( http: / / www.21cnjy.com / );
(2)120×(50%+30%)=96(人),
故答案为:96;
(3)1800×(50%+30%)=1440(人),
答:此次测试中,全校达标的人数约为1440人.
【点睛】
本题考查了扇形统计图与条形统计图,用样本估计总体等知识,根据两幅统计图提供的公共信息得到样本容量是解题关键.21世纪教育网版权所有
5、(1),;(2)见解析;(3)1440名
【分析】
(1)样本容量=60÷0.2=300,90÷300=n;
(2)计算300×0.4=12,补图即可;
(3)用优秀率×2400,计算即可.
【详解】
解:(1)根据题意,得:60÷0.2=300(人),
∴90÷300=n=0.3;
故答案为:300, 0.3;
(2)∵300×0.4=120(人),
∴补图如下:
( http: / / www.21cnjy.com / )
(3)根据题意,优秀率为0.4+0.2,
∴(人),
答:该校2400名学生中竞赛成绩为“优秀”的有1440名.
【点睛】
本题考查了频数分布直方图,样本估计整体,正确理解样本容量,频数,频率之间的关系是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
九年级数学第二学期第二十八章统计初步专题攻克
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内 ( http: / / www.21cnjy.com )相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。2·1·c·n·j·y
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、甲、乙、丙、丁四名同学进行立定跳远测试,每人10次立定跳远成绩的平均数都是2.25米,方差分别是,,,,则这四名同学立定跳远成绩最稳定的是( ).
A.甲 B.乙 C.丙 D.丁
2、下列命题正确的是( )
A.数轴上的每一个点都表示一个有理数
B.甲、乙两人五次考试平均成绩相同,且,,则乙的成绩更稳定
C.三角形的一个外角大于任意一个内角
D.在平面直角坐标系中,点与点关于x轴对称
3、下列说法中,正确的是( )
A.若,,则
B.90′=1.5°
C.过六边形的每一个顶点有4条对角线
D.疫情防控期间,要掌握进入校园人员的体温是否正常,可采用抽样调查
4、某县为了传承中华优秀传统文化,组织了一 ( http: / / www.21cnjy.com )次全县600名学生参加的“中华经典诵读”大赛.为了解本次大赛的选手成绩,随机抽取了其中50名选手的成绩进行统计分析.在这个问题中,下列说法中正确的是( )
A.这600名学生的“中华经典诵读”大赛成绩的全体是总体
B.50名学生是总体的一个样本
C.每个学生是个体
D.样本容量是50名
5、下列调查中,适合采用全面调查的是( )
A.了解一批电灯泡的使用寿命 B.调查榆林市中学生的视力情况
C.了解榆林市居民节约用水的情况 D.调查“天问一号”火星探测器零部件的的质量
6、根据下面的两幅统计图,你认为哪种说法不合理( )
( http: / / www.21cnjy.com / )
A.六(2)班女生人数一定比六(1)班多 B.两个班女生人数可能同样多
C.六(2)班女生人数可能比六(1)班多 D.六(2)班女生人数一定比男生多
7、某中学规定学生的学期 ( http: / / www.21cnjy.com )体育成绩满分为100分,其中课外体育占20%,期中考试成绩占30%,期末考试成绩占50%.小彤的三项成绩(百分制)依次为95,90,88,则小彤这学期的体育成绩为( )
A.89 B.90 C.91 D.92
8、为了了解2017年我县九年级6023名学生学业水平考试的数学成绩,从中随机抽取了200名学生的数学成绩,下列说法正确的是( )【出处:21教育名师】
A.2017年我县九年级学生是总体 B.每一名九年级学生是个体
C.200名九年级学生是总体的一个样本 D.样本容量是200
9、某校男子足球队的年龄分布如图条形图所示,则这些队员年龄的众数是( )
( http: / / www.21cnjy.com / )
A.8 B.13 C.14 D.15
10、甲、乙、丙、丁四位同学都参加了5次数学模拟测试,每个人这5次成绩的平均数都是92分,方差分别是,,,,则这5次测试成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、为庆祝中国共产党建党一百周年,某 ( http: / / www.21cnjy.com )单位党支部开展“学史明理,学史增信,学史崇德,学史力行”读书活动,学习小组抽取了七名党员5天的学史的时间(单位:h)分别为:4,3,3,5,6,5,5,这组数据的众数是________.
2、新兴农场果农随机从甲、乙、丙三个品种的枇杷树中各选10棵,每棵产量的平均数(单位:千克)及方差(单位:千克)如下表所示,他准备从这三个品种中选出一种产量既高又稳定的枇杷树进行种植,则应选的品种是______.
甲 乙 丙
44 44 42
1.7 1.5 1.7
3、对于两组数据来说,可 ( http: / / www.21cnjy.com )从平均数和方差两个方面进行比较,平均数反映一组数据的______,方差则反映一组数据在平均数左右的______,因此从平均数看或从方差看,各有长处.
4、小丽的笔试成绩为90分,面试成绩为95分,若笔试成绩、面试成绩按6:4计算平均成绩,则小丽的平均成绩是 _______分.
5、圆周率π≈3.141592653589793,数字5出现的频数是____.
三、解答题(5小题,每小题10分,共计50分)
1、为促进学生健康成长,帮助 ( http: / / www.21cnjy.com )家长解决按时接送学生困难的问题,认真落实全国教育大会精神,某校结合自身情况,在开展中学生课后服务工作方面做了全面规划,并且落到实处.在不加重学生课业负担的前提下,学校在托管时间内组织学生进行自主阅读、体育、艺术、及其他一些有益身心健康的活动,学生根据自己的喜好,自主选择.学校随机抽取了部分学生进行调查(抽取的学生都选择了一种自己喜爱的活动),下面是根据调查情况,得到的两幅不完整的统计图,请结合图中信息解答下列问题:21*cnjy*com
( http: / / www.21cnjy.com / )
(1)求出本次调查中,随机抽取的学生人数;
(2)补全条形统计图,并求出“其他”所对应的圆心角的度数;
(3)若该校学生总人数为840人,估计选择阅读的学生有多少人?
2、某学校为了调查学生利用“天天跳绳” ( http: / / www.21cnjy.com )APP锻炼身体的使用频率,随机抽取了部分学生,利用调查问卷进行抽样调查:用“A”表示“一周5次”,“B”表示“一周4次”,“C”表示“一周3次”,“D”表示“一周2次”(必须选且只选一项),如图是工作人员根据问卷调查统计资料绘制的两幅不完整的统计图,请你根据统计图提供的信息回答以下问题:
( http: / / www.21cnjy.com / )
(1)本次调查中,共调查了多少人?
(2)将图(2)补充完整;
(3)如果该学校有学生1000人,请你估计该学校学生利用“天天跳绳”APP锻炼身体的使用频率是“一周2次”的约有多少人?
3、根据公安部交管局下发的通知,春 ( http: / / www.21cnjy.com )节前开展一次“一带一盔”安全守护行动,其中要求骑行摩托车、电动车需要佩戴头盔,某日交警部门在某个十字路口共拦截了50名不带头盔的骑行者,根据年龄段和性别得到如下表的统计信息,根据表中信息回答下列问题:
年龄x(岁) 人数 男性占比
x<20 4 50%
20≤x<30 m 60%
30≤x<40 25 60%
40≤x<50 8 75%
x≥50 3 100%
(1)统计表中m的值为 ;
(2)若要按照表格中各年龄段的人数来绘制扇形统计图,则年龄在“30≤x<40”部分所对应扇形的圆心角的度数为 ;
(3)若从年龄在“x<20”的4人中随机抽取2人参加交通安全知识学习,请用列表或画树状图的方法,求恰好抽到1名男性和1名女性的概率.
4、为了了解我校学生对英语单词掌握的情况 ( http: / / www.21cnjy.com ),现对全校学生进行英语百词测试,为了了解测试结果,随机抽取部分学生的成绩进行分析,现将成绩分为三个等级:不合格、一般、优秀,并绘制成如下两幅统计图(不完整).请根据图中所给的信息解答下列问题:
( http: / / www.21cnjy.com / )
(1)本次随机抽取的人数是 人 ,并将以上两幅统计图补充完整;
(2)若“一般”和“优秀”均被视为达标成绩,则我校被抽取的学生中有 人达标;
(3)若我校学生有1800人,请你估计此次测试中,全校达标的学生有多少人?
5、为深入开展青少年毒品预防教育工 ( http: / / www.21cnjy.com )作,增强学生禁毒意识,某校联合禁毒办组织开展了“2021青少年禁毒知识竞赛”活动,并随即抽查了部分同学的成绩,整理并制作成图表如下:
( http: / / www.21cnjy.com / ) ( http: / / www.21cnjy.com / )
根据以上图表提供的信息,回答下列问题:
(1)抽查的人数为______人,______;
(2)请补全频数分布直方图;
(3)若成绩在80分以上(包括80分)为“优秀”,请你估计该校2400名学生中竞赛成绩是“优秀”的有多少名?21*cnjy*com
-参考答案-
一、单选题
1、D
【分析】
平均数相同,方差值越小越稳定,比较四名同学方差值的大小即可.
【详解】
解:∵
∴丁同学的成绩最稳定
故选D.
【点睛】
本题考查了方差.解题的关键在于理解方差值越小的数据越稳定.
2、D
【分析】
根据数轴上的点与实数一一对应即可判断A;根据平均数相同的情形下,方差越小,成绩越稳定即可判断B;根据三角形的外角与内角的关系即可判断C;根据关于轴对称的点的坐标特征即可判断D
【详解】
A. 数轴上的每一个点都表示一个实数,故该选项不正确,不符合题意;
B. 甲、乙两人五次考试平均成绩相同,且,,则甲的成绩更稳定,故该选项不正确,不符合题意;
C. 三角形的一个外角不一定大于任意一个内角,故该选项不正确,不符合题意;
D. 在平面直角坐标系中,点与点关于x轴对称,故该选项正确,符合题意;
故选D
【点睛】
本题考查了实数与数轴,方差的意义,三角形的外角的性质,关于轴对称的点的坐标特征,掌握以上知识是解题的关键.21·cn·jy·com
3、B
【分析】
由等式的基本性质可判断A,由 可判断B,由过边形的一个顶点可作条对角线可判断C,由全面调查与抽样调查的含义可判断D,从而可得答案.
【详解】
解:若,则故A不符合题意;
90′=故B符合题意;
过六边形的每一个顶点有3条对角线,故C不符合题意;
疫情防控期间,要掌握进入校园人员的体温是否正常,事关重大,一定采用全面调查,故D不符合题意;
故选:B.
【点睛】
本题考查的是等式的基本性质,角度的换算,多边形的对角线问题,全面调查与抽样调查的含义,掌握以上基础知识是解本题的关键.21教育网
4、A
【分析】
根据总体的定义:表示考察的全体对象;样本 ( http: / / www.21cnjy.com )的定义:按照一定的抽样规则从总体中取出的一部分个体,样本中个体的数目称为样本容量;个体的定义:总体中每个成员成为个体,进行逐一判断即可.
【详解】
解:A、这600名学生的“中华经典诵读”大赛成绩的全体是总体,故本选项正确,符合题意;
B、50名学生的成绩是总体的一个样本,故本选项错误,不符合题意;
C、每个学生的成绩是个体,故本选项错误,不符合题意;
D、样本容量是50,故本选项错误,不符合题意;
故选A.
【点睛】
本题主要考查了样本,总体,个体和样本容量的定义,解题的关键在于熟知相关定义.
5、D
【分析】
由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似,再逐一分析即可.21cnjy.com
【详解】
解:A.了解一批电灯泡的使用寿命,具有破坏性,适合抽样调查,不符合题意;
B.调查榆林市中学生的视力情况,适合抽样调查,不符合题意;
C.了解榆林市居民节约用水的情况,适合抽样调查,不符合题意;
D.调查“天问一号”火星探测器零部件的的质量,必需采用全面调查,符合题意;
故选:D.
【点睛】
本题考查了抽样调查和全面 ( http: / / www.21cnjy.com )调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.【版权所有:21教育】
6、A
【分析】
根据两个扇形统计图,只能得到两个班级男女生比例的大小,无法确定男生和女生的具体人数,由此即可得.
【详解】
解:∵两个班的人数不知道,
∴无法确定每个班的男生和女生的具体人数,
∴六(2)班女生人数一定比六(1)班多不合理,
故选:A.
【点睛】
题目主要考查从扇形统计图获取信息,理解题意,掌握扇形统计图表示的意义是解题关键.
7、B
【分析】
根据加权平均数的计算公式列出算式,再进行计算即可.
【详解】
解:根据题意得:
95×20%+90×30%+88×50%=90(分).
即小彤这学期的体育成绩为90分.
故选:B.
【点睛】
此题考查了加权平均数,掌握加权平均数的计算公式是本题的关键,是一道常考题.
8、D
【分析】
总体是指考查的对象的全体,个体是总体中的每 ( http: / / www.21cnjy.com )一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.根据总体、个体、样本、样本容量的定义,做出判断.
【详解】
解: 2017年我县九年级学生的数学成绩是总体,故A不符合题意;
每一名九年级学生的数学成绩是个体,故B不符合题意;
200名九年级学生的数学成绩是总体的一个样本,故C不符合题意;
样本容量是200,故D符合题意;
故选D
【点睛】
考查了总体、个体、样本、样 ( http: / / www.21cnjy.com )本容量,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.2-1-c-n-j-y
9、C
【分析】
根据众数的定义:一组数据中出现次数最多的那个数,称为这组数据的众数,据此结合条形图可得答案.
【详解】
解:由条形统计图知14岁出现的次数最多,
所以这些队员年龄的众数为14岁,
故选C.
【点睛】
本题考查了众数的定义及条形统计图的知识,解题的关键是能够读懂条形统计图及了解众数的定义.
10、D
【分析】
根据方差越大,则数据的离散程度越大,稳定性也越小;反之,则数据的离散程度越小,稳定性越好,进而分析即可.21·世纪*教育网
【详解】
解:∵,,,,
∴S丁2<S丙2<S乙2<S甲2,
∴成绩最稳定的是丁.
故选:D.
【点睛】
本题考查了方差的意义,方差是用来衡 ( http: / / www.21cnjy.com )量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,数据越稳定.
二、填空题
1、5h
【分析】
根据众数的意义(出现次数最多的数据是众数)可得答案.
【详解】
解:这组数据中出现次数最多的是5h,共出现3次,
所以众数是5h,
故答案为:5h.
【点睛】
本题考查众数,理解众数的意义是解决问题的关键.
2、乙
【分析】
先比较平均数得到甲和乙产量较高,然后比较方差得到乙比较稳定.
【详解】
解:因为甲、乙的平均数比丙大,所以甲、乙的产量较高,
又乙的方差比甲小,所以乙的产量比较稳定,
即从这三个品种中选出一种产量既高又稳定的枇杷树进行种植,则应选的品种是乙;
故答案为:乙.
【点睛】
本题考查了方差:一组数据中各数据与它 ( http: / / www.21cnjy.com )们的平均数的差的平方的平均数,叫做这组数据的方差.方差是反映一组数据的波动大小的一个量.方差越大,则与平均值的离散程度越大,稳定性也越差;反之,则它与其平均值的离散程度越小,稳定性越好.也考查了平均数.www.21-cn-jy.com
3、一般水平 波动大小
【分析】
根据平均数和方差的意义进行回答即可.
【详解】
解:平均数反映一组数据的一般水平,方差则反映一组数据在平均数左右的波动大小,
故答案为:一般水平;波动大小
【点睛】
本题考查了平均数和方差的区别,熟练掌握平均数和方差的意义是解答本题的关键.
4、92
【分析】
根据加权平均数的定义和计算公式计算可得.
【详解】
解:小丽的平均成绩是=92(分).
故答案为:92.
【点睛】
本题主要考查加权平均数,解题的关键是熟练掌握加权平均数的定义和计算公式.
5、3
【分析】
从数5出现的次数即可得出答案.
【详解】
在中,5出现了3次,
∴数字5出现的频数是3.
故答案为:3.
【点睛】
本题考查频数的定义:一组数据中,某数据出现的次数,掌握频数的定义是解题的关键.
三、解答题
1、(1)120人;(2)见解析,36°;(3)126人
【分析】
(1)从条形图选择体育的人数÷从扇形图中体育所占百分比计算即可;
(2)从调查总人数减去阅读,体育和其它得出艺术人数,补画条形图,再求出其它12人除以120得出所占百分比,再乘以360°即可;【来源:21·世纪·教育·网】
(3)先计算样本中选择阅读所占样本的百分比,再用样本中所含百分比乘以总数估计总体中的含量即可.
【详解】
解:(1)本次调查中从条形图得出选择体育有54人,从扇形统计图中体育所占百分比为45%,
本次调查人数为:(人);
(2)∵艺术:(人),
∴补全的条形统计图如下图所示:
( http: / / www.21cnjy.com / )
“其他”所对应的圆心角度数为;
(3)样本中选择阅读的人数为18人,占样本的百分比为,
该校学生总人数为840人,估计选择阅读的学生有:(人),
∴选择“阅读”的学生大约有126人.
【点睛】
本题考查从条形图和扇形统计图获取信 ( http: / / www.21cnjy.com )息和处理信息能力,样本容量,补画条形图,扇形圆心角,用样本的百分比含量估计总体中的数量,掌握以上知识是解题关键.www-2-1-cnjy-com
2、(1)人;(2)补全图形见解析;(3)人
【分析】
(1)由C组有100人,占比列式计算后可得答案;
(2)先求解B组人数,再补全图形即可;
(3)由总人数1000乘以D组“一周2次”的占比即可得到答案.
【详解】
解:(1)由C组有100人,占比 可得:
本次调查中,共调查人.
(2)B组人数有人,
补全图形如下:
( http: / / www.21cnjy.com / )
(3)该学校有学生1000人,该学校学生利用“天天跳绳”APP锻炼身体的使用频率是“一周2次”的约有:人.【来源:21cnj*y.co*m】
【点睛】
本题考查的是从扇形图与条形图中获取信息,补全条形统计图,利用样本估计总体,理解扇形图与条形图中关联信息是解本题的关键.21教育名师原创作品
3、
(1)10
(2)180°
(3)见解析,
【分析】
(1)根据总数减去表格中其他数据即可求解;
(2)根据年龄在“30≤x<40”的人数占总人数的比例乘以360°即可求解;
(3)用列表法求概率即可.
(1)
故答案为:10
(2)
故答案为:
(3)
设两名男性用表示,两名女性用表示,根据题意,列表如下,
由上表可知,共有12种等可能的结果,符合条件的结果有8种,
故P(恰好抽到1名男性和1名女性)=
【点睛】
本题考查了求扇形统计图的圆心角的度数,求频数,根据列表法求概率,理解题意,掌握以上知识是解题的关键.
4、(1)120,统计图补充见详解;(2)96;(3)1440人.
【分析】
(1)用不合格人数24除以占比20%即可求出 ( http: / / www.21cnjy.com )抽取人数未120人,用1减去优秀占比和不合格占比即可求出一般占比,用120乘以优秀占比50%即可求出优秀人数,再补充两幅统计图即可;
(2)用120乘以优秀与一般占比之和,即可求出抽取学生中达标人数;
(3)用1800乘以优秀与一般占比之和,即可估算出全校达标学生数.
【详解】
解:(1)24÷20%=120(人),1-50%-20%=30%,120×50%=60(人),
故答案为:120,
统计图补充如图:
( http: / / www.21cnjy.com / );
(2)120×(50%+30%)=96(人),
故答案为:96;
(3)1800×(50%+30%)=1440(人),
答:此次测试中,全校达标的人数约为1440人.
【点睛】
本题考查了扇形统计图与条形统计图,用样本估计总体等知识,根据两幅统计图提供的公共信息得到样本容量是解题关键.21世纪教育网版权所有
5、(1),;(2)见解析;(3)1440名
【分析】
(1)样本容量=60÷0.2=300,90÷300=n;
(2)计算300×0.4=12,补图即可;
(3)用优秀率×2400,计算即可.
【详解】
解:(1)根据题意,得:60÷0.2=300(人),
∴90÷300=n=0.3;
故答案为:300, 0.3;
(2)∵300×0.4=120(人),
∴补图如下:
( http: / / www.21cnjy.com / )
(3)根据题意,优秀率为0.4+0.2,
∴(人),
答:该校2400名学生中竞赛成绩为“优秀”的有1440名.
【点睛】
本题考查了频数分布直方图,样本估计整体,正确理解样本容量,频数,频率之间的关系是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
