沪教版(上海)九年级数学第二学期第二十八章统计初步章节测试试题(含答案解析)
文档属性
| 名称 | 沪教版(上海)九年级数学第二学期第二十八章统计初步章节测试试题(含答案解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-24 14:12:16 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
九年级数学第二学期第二十八章统计初步章节测试
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指 ( http: / / www.21cnjy.com )定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。21教育网
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、某县为了传承中华优秀传统文化,组 ( http: / / www.21cnjy.com )织了一次全县600名学生参加的“中华经典诵读”大赛.为了解本次大赛的选手成绩,随机抽取了其中50名选手的成绩进行统计分析.在这个问题中,下列说法中正确的是( )21*cnjy*com
A.这600名学生的“中华经典诵读”大赛成绩的全体是总体
B.50名学生是总体的一个样本
C.每个学生是个体
D.样本容量是50名
2、下列命题正确的是( )
A.数轴上的每一个点都表示一个有理数
B.甲、乙两人五次考试平均成绩相同,且,,则乙的成绩更稳定
C.三角形的一个外角大于任意一个内角
D.在平面直角坐标系中,点与点关于x轴对称
3、小明抛一枚硬币100次,其中有60次正面朝上,则反面朝上的频率是( )
A.0.6 B.6 C.0.4 D.4
4、某养羊场对200头生羊量进行统计, ( http: / / www.21cnjy.com )得到频数直方图(每一组含前一个边界值,不含后一个边界值)如图所示,其中质量在77.5kg及以上的生羊的只数是( )【出处:21教育名师】
( http: / / www.21cnjy.com / )
A.180 B.140 C.120 D.110
5、为了解甲、乙、丙、丁四位选手 ( http: / / www.21cnjy.com )射击水平,随机让四人各射击10次,计算四人10次射击命中环数平均数都是9.3环,方差(环2)如下表.则这四位选手成绩最稳定的是( )
选手 甲 乙 丙 丁
方差 0.035 0.016 0.022 0.025
A.甲 B.乙 C.丙 D.丁
6、在一次科技作品制作比赛中,某小组 ( http: / / www.21cnjy.com )八件作品的成绩(单位:分)分别是:7,10,9,8,7,9,9,8.对这组数据,下列说法正确的是( )2-1-c-n-j-y
A.平均数是8 B.众数是8.5 C.中位数8.5 D.极差是5
7、在一次班级体测调查中,收集到4 ( http: / / www.21cnjy.com )0名同学的跳高数据,数据分别落在5个组内,且落入第一、二、三、五组的数据个数分别为2、7、11、12,则第四组频数为( ).
A.9 B.8 C.7 D.6
8、下列问题不适合用全面调查的是( )
A.旅客上飞机前的安检 B.企业招聘,对应试人员进行面试
C.了解全班同学每周体育锻炼的时间 D.调查市场上某种食品的色素含量是否符合国家标准
9、八(3)班七个兴趣小组人数分别为4、4、5、、6、6、7,已知这组数据的平均数是5,则这组数据的中位数是( )
A.6 B.5 C.4 D.3
10、一个班有40名学生 ( http: / / www.21cnjy.com ),在一次身体素质测试中,将全班学生的测试结果分为优秀、合格、不合格.测试结果达到优秀的有18人,合格的有17人,则在这次测试中,测试结果不合格的频率是( )
A.0.125 B.0.30 C.0.45 D.1.25
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、某中学期中考试,八(1)班第一小组10人数学考试的成绩为:100分3人,90分5人,80分2人,则全组数学平均成绩为_____分.
2、小玲家的鱼塘里养了2 500条鲢鱼,按经 ( http: / / www.21cnjy.com )验,鲢鱼的成活率约为80%.现准备打捞出售,为了估计鱼塘中鲢鱼的总质量,从鱼塘中捕捞了3次进行统计,得到的数据如下表:
鱼的条数 平均每条鱼的质量
第一次捕捞 20
第二次捕捞 10
第三次捕捞 10
那么,鱼塘中鲢鱼的总质量约是________kg.
3、已知一组数据:18,17,13,15,17,16,14,17,则这组数据的中位数与众数分别是__________.
4、七年级(5)班20名女生的身高如下(单位:cm):
153 156 152 158 156 160 163 145 152 153
162 153 165 150 157 153 158 157 158 158
(1)请你在下表中填出身高在以下各个范围的频数,百分比(每个范围包含下限,但不包含上限):
身高(cm) 140~150 150~160 160~170
频数
百分比
(2)上表把身高分成___组,组距是___;
(3)身高在___范围的人数最多.
5、某同学对全班50名同学感兴趣的课外活动项目进行了调查,绘制下表:
活动项目 体育运动 学科兴趣小组 音乐 舞蹈 美术
人数(人) 15 12 10 5 8
(1)全班同学最感兴趣的课外活动项目是______;
(2)对音乐感兴趣的人数是____,占全班人数的百分比是_______.
三、解答题(5小题,每小题10分,共计50分)
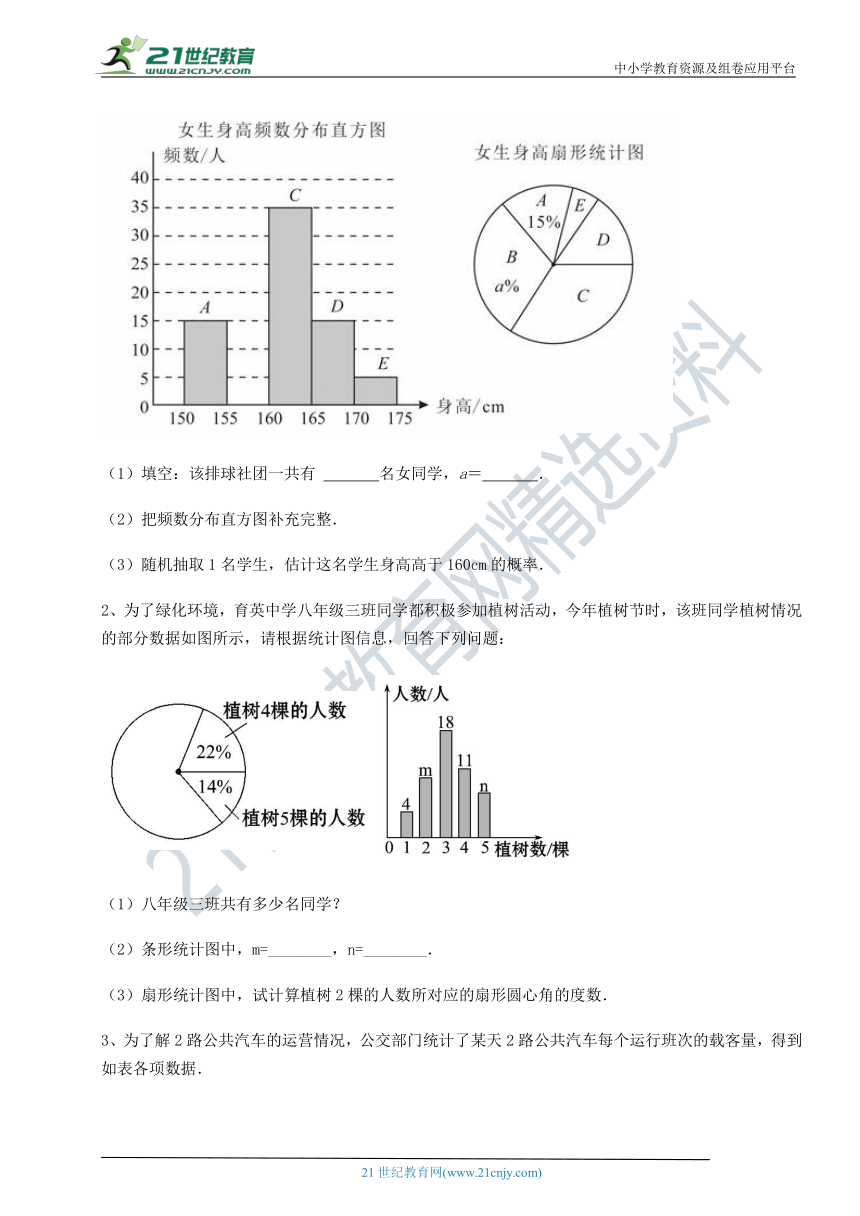
1、山西某高校为了弘扬女排精神 ( http: / / www.21cnjy.com ),组建了女排社团,通过测量女同学的身高(单位:cm),并绘制了两幅不完整的统计图,请结合图中提供的信息,解答下列问题.21世纪教育网版权所有
( http: / / www.21cnjy.com / )
(1)填空:该排球社团一共有 名女同学,a= .
(2)把频数分布直方图补充完整.
(3)随机抽取1名学生,估计这名学生身高高于160cm的概率.
2、为了绿化环境,育英中学八年级三班同 ( http: / / www.21cnjy.com )学都积极参加植树活动,今年植树节时,该班同学植树情况的部分数据如图所示,请根据统计图信息,回答下列问题:【版权所有:21教育】
( http: / / www.21cnjy.com / ) ( http: / / www.21cnjy.com / )
(1)八年级三班共有多少名同学?
(2)条形统计图中,m=________,n=________.
(3)扇形统计图中,试计算植树2棵的人数所对应的扇形圆心角的度数.
3、为了解2路公共汽车的运营情况,公交部门统计了某天2路公共汽车每个运行班次的载客量,得到如表各项数据.
载客量/人 组中值 频数(班次)
1≤x<21 11 2
21≤x<41 a 8
41≤x<61 b 20
(1)求出表格中a=_______,b=______.
(2)计算该2路公共汽车平均每班的载客量是多少
4、某校七年级为了解学生课堂发言情况, ( http: / / www.21cnjy.com )随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下,并绘制了如图所示的两幅不完整的统计图,请结合图中相关数据回答下列问题:【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com / )
组别 发言次数n
A
B
C
D
E
F
(1)直接写出随机抽取学生的人数为______人;
(2)直接补全频数直方图;
(3)求扇形统计图中B部分所对应的百分比和F部分扇形圆心角的度数;
(4)该校七年级共有学生1000人,请估计七年级学生这天在课堂上发言次数大于等于12次的人数.
5、八(2)班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲 7 8 9 7 10 10 9 10 10 10
乙 10 8 7 9 8 10 10 9 10 9
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是 队.
-参考答案-
一、单选题
1、A
【分析】
根据总体的定义:表示考察的全体 ( http: / / www.21cnjy.com )对象;样本的定义:按照一定的抽样规则从总体中取出的一部分个体,样本中个体的数目称为样本容量;个体的定义:总体中每个成员成为个体,进行逐一判断即可.
【详解】
解:A、这600名学生的“中华经典诵读”大赛成绩的全体是总体,故本选项正确,符合题意;
B、50名学生的成绩是总体的一个样本,故本选项错误,不符合题意;
C、每个学生的成绩是个体,故本选项错误,不符合题意;
D、样本容量是50,故本选项错误,不符合题意;
故选A.
【点睛】
本题主要考查了样本,总体,个体和样本容量的定义,解题的关键在于熟知相关定义.
2、D
【分析】
根据数轴上的点与实数一一对应即可判断A;根据平均数相同的情形下,方差越小,成绩越稳定即可判断B;根据三角形的外角与内角的关系即可判断C;根据关于轴对称的点的坐标特征即可判断D
【详解】
A. 数轴上的每一个点都表示一个实数,故该选项不正确,不符合题意;
B. 甲、乙两人五次考试平均成绩相同,且,,则甲的成绩更稳定,故该选项不正确,不符合题意;
C. 三角形的一个外角不一定大于任意一个内角,故该选项不正确,不符合题意;
D. 在平面直角坐标系中,点与点关于x轴对称,故该选项正确,符合题意;
故选D
【点睛】
本题考查了实数与数轴,方差的意义,三角形的外角的性质,关于轴对称的点的坐标特征,掌握以上知识是解题的关键.2·1·c·n·j·y
3、C
【分析】
先求出反面朝上的频数,然后根据频率=频数÷总数求解即可
【详解】
解:∵小明抛一枚硬币100次,其中有60次正面朝上,
∴小明抛一枚硬币100次,其中有40次反面朝上,
∴反面朝上的频率=40÷100=0.4,
故选C.
【点睛】
本题主要考查了根据频数求频率,解题的关键在于能够熟练掌握频率=频数÷总数.
4、B
【分析】
根据题意和直方图中的数据可以求得质量在77.5kg及以上的生猪数,本题得以解决.
【详解】
解:由直方图可得,
质量在77.5kg及以上的生猪:90+30+20=140(头),
故选B.
【点睛】
本题考查频数分布直方图,解答本题的关键是明确题意,利用数形结合的思想解答.
5、B
【分析】
根据方差越小越稳定,比较后,选择即可.
【详解】
∵乙的方差最小,
∴乙最稳定,
故选B.
【点睛】
本题考查了方差的意义,正确理解方差越小越稳定是解题的关键.
6、C
【分析】
计算这组数据的平均数、众数、中位数及极差即可作出判断.
【详解】
这组数据的平均数为:,众数为9,中位数为8.5,极差为10-7=3,故正确的是中位数为8.5.
故选:C
【点睛】
本题考查了反映一组数据平均数、众数、中位数、极差等知识,正确计算这些统计量是关键.
7、B
【分析】
根据题意可得:共40个数据,知道一、二、三、五组的数据个数,用总数减去这几组频数,即可得到答案.
【详解】
解:由题意得:第四组的频数=40-(2+7+11+12)=8;
故选B.
【点睛】
本题是对频数的考查,掌握各小组频数之和等于数据总和是解题的关键.
8、D
【分析】
由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似,根据以上逐项分析可知.21·cn·jy·com
【详解】
解:A. 旅客上飞机前的安检,人员不多,且这个调查很重要不可漏掉任何人,适合全面调查,不符合题意, 21·世纪*教育网
B. 企业招聘,对应试人员进行面试,人员不多,且这个调查很重要不可漏掉任何人,适合全面调查,不符合题意,www-2-1-cnjy-com
C. 了解全班同学每周体育锻炼的时间,人员不多,适合全面调查,不符合题意,
D. 调查市场上某种食品的色素含量是否符合国家标准,调查具有破坏性,不适合全面调查,符合题意
故选D
【点睛】
本题考查的是全面调查与抽样调查, ( http: / / www.21cnjy.com )在调查实际生活中的相关问题时,要灵活处理,既要考虑问题本身的需要,又要考虑实现的可能性和所付出代价的大小.理解全面调查与抽样调查的适用范围是解题的关键.21教育名师原创作品
9、B
【分析】
本题可先算出x的值,再把数据按从小到大的顺序排列,找出最中间的数,即为中位数.
【详解】
解:∵某班七个兴趣小组人数分别为4,4,5,x,6,6,7.已知这组数据的平均数是5,
∴x=5×7 4 4 5 6 6 7=3,
∴这一组数从小到大排列为:3,4,4,5,6,6,7,
∴这组数据的中位数是:5.
故选:B.
【点睛】
本题考查的是中位数和平均数的定义,熟知中位数的定义是解答此题的关键.
10、A
【分析】
先求得不合格人数,再根据频率的计算公式求得不合格人数的频率即可.
【详解】
解:不合格人数为(人,
不合格人数的频率是,
故选:A.
【点睛】
本题主要考查了频率与概率,解题的关键是掌握频率是指每个对象出现的次数与总次数的比值(或者百分比).
二、填空题
1、91
【分析】
根据平均数公式计算.
【详解】
解:(分),
故答案为:91.
【点睛】
此题考查平均数的计算公式,熟记计算公式是解题的关键.
2、3600
【分析】
首先计算样本平均数,然后计算成活的鱼的数量,最后两个值相乘即可.
【详解】
解:每条鱼的平均重量为:千克,
成活的鱼的总数为:条,
则总质量约是千克.
故答案为:3600.
【点睛】
本题考查了利用样本估计总体,解题的关键是注意样本平均数的计算方法:总质量总条数,能够根据样本估算总体.21cnjy.com
3、16.5,17
【分析】
根据众数和中位数的定义求解即可,中 ( http: / / www.21cnjy.com )位数:将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数.如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.众数:在一组数据中出现次数最多的数.
【详解】
将,,,,,,,从小到大排列为:,,,,,,,
其中出现的次数最多,则众数为,
中位数为:.
故答案为:;
【点睛】
本题考查了求众数和中位数,理解众数和中位数的定义是解题的关键.
4、3
10 150~160
【分析】
(1)找出各个组中的人数,然后除以总人数即可得出所占百分比;
(2)通过所给的数据把各个范围中的人数填入相应表格,根据所填写的信息及题意确定分成的组数、组距;
(3)根据所填信息确定身高在哪个范围的人数最多即可.
【详解】
(1)填表:
身高(cm) 140~150 150~160 160~170
频数 1 15 4
百分比 5% 75% 20%
(2)上表把身高分成3组,组距是10;
(3)身高在范围最多.
【点睛】
本题考查的是从统计图表中获取信息,关键是找出各个组中的人数,通过所给的数据把各个范围中的人数填入相应表格,然后据此得出相关结论.www.21-cn-jy.com
5、体育运动 10
【分析】
(1)从统计表中直接通过比较即可得到.
(2)利用统计表,找到对音乐感兴趣的人数,再用对音乐感兴趣的人数除以全班人数,求出对应的百分比.
【详解】
解:从统计表分析人数可得到结论.由表可得:
(1)体育运动小组人数最多,所以全班同学最感兴趣的课外活动项目是体育运动;
(2)对音乐感兴趣的人数是10,占全班人数的百分比是10÷50=.
故答案为:(1)体育运动;(2)10,
【点睛】
本题主要是统计表的相关知识,如何读懂统计表,从统计表获取信息是关键.
三、解答题
1、(1)100,30;(2)见解析;(3)0.55
【分析】
(1)根据频数分布直方图中组的人数除以扇形统计图中组的所占百分比即可求得总人数,根据总人数减去组的人数即可求得组的人数,除以总人数即可求得的值;
(2)根据(1)中的结论补全统计图即可;
(3)根据身高高于160cm除以总人数即可求得随机抽取1名学生,估计这名学生身高高于160cm的概率【来源:21·世纪·教育·网】
【详解】
解:(1)总人数为:;
组的人数为
故答案为:
(2)如图,
( http: / / www.21cnjy.com / )
(3)总人数为,身高高于160cm为
随机抽取1名学生,估计这名学生身高高于160cm的概率为
【点睛】
本题考查了频数直方图和扇形统计图信息关联,简单概率计算,从统计图中获取信息是解题的关键.
2、
(1)50人;
(2) 10 7
(3)72°
【分析】
(1)根据植4株的有11人,所占百分比为,求出总人数;
(2)根据植树5棵人数所占的比例来求的值;用总人数减去其它植树的人数,就是的值,从而补全统计图;
(3)根据植树2棵的人数所占比例,即可得出圆心角的比例相同,即可求出圆心角的度数.
(1)
解:由两图可知,植树4棵的人数是11人,占全班人数的,所以八年级三班共有人数为:(人.
(2)
解:由扇形统计图可知,植树5棵人数占全班人数的,
所以(人.
(人.
故答案是:10;7;
(3)
解:所求扇形圆心角的度数为:
【点睛】
本题主要考查了扇形统计图的综合运用,解题的关键是读懂统计图,从不同的统计图中得到必要的信息,扇形统计图直接反映部分占总体的百分比大小.
3、(1)31;51;(2)43人.
【分析】
(1)利用组中值的计算方程直接计算即可得;
(2)利用组中值表示各组的平均数,然后根据加权平均数的计算方法求解即可.
【详解】
解:(1),
,
故答案为:31;51;
(2)(人),
答:该2路公共汽车平均每班的载客量是43人.
【点睛】
题目主要考查组中值及加权平均数的计算方法,理解题意,掌握组中值及加权平均数的计算方法是解题关键.
4、(1)50;(2)补全频数直方图见解析;(3)B部分所对应的百分比;F部分扇形圆心角的度数为;(4)180人.
【分析】
(1)用A组频数除以频率,即可求得抽取人数为50人;
(2)用50乘以C组所占百分比求出频数,用50减A、B、C、D、E组频数,即可求解,补全直方图即可;
(3)用B组频数除以50,即可求解;用F组频数除以50再乘以360°即可求解;
(4)用样本估计总体,用1000乘以样本中发言次数大于等于12的人数所占百分比,问题得解.
【详解】
(1)3÷6%=50,
故答案为:50;
(2)50×30%=15, 50-3-10-15-13-4=5,补全频数直方图如下;
( http: / / www.21cnjy.com / )
(3)B部分所对应的百分比,
F部分扇形圆心角的度数为;
(4)(人),
答:估计该校七年级学生1000人中,这天在课堂上发言次数大于等于12次的人数为180人.
【点睛】
本题考查了直方图,扇形图,用样本估计总体等知识,理解直方图、扇形图的意义,根据两种统计图中提供的公共信息求出样本容量是解题关键.
5、(1)9.5,10;(2)平均成绩9分,方差1;(3)乙
【分析】
(1)根据中位数的定义求出最中间两个数的平均数;根据众数的定义找出出现次数最多的数即可;
(2)先求出乙队的平均成绩,再根据方差公式进行计算;
(3)先比较出甲队和乙队的方差,再根据方差的意义即可得出答案.
【详解】
解:(1)把甲队的成绩从小 ( http: / / www.21cnjy.com )到大排列为:7,7,8,9,9,10,10,10,10,10,最中间两个数的平均数是(9+10)÷2=9.5(分),21*cnjy*com
则中位数是9.5分;
乙队成绩中10出现了4次,出现的次数最多,
则乙队成绩的众数是10分;
故答案为:9.5,10;
(2)乙队的平均成绩是:×(10×4+8×2+7+9×3)=9,
则方差是:×[4×(10﹣9)2+2×(8﹣9)2+(7﹣9)2+3×(9﹣9)2]=1;
(3)∵甲队成绩的方差是1.4,乙队成绩的方差是1,
∴成绩较为整齐的是乙队;
故答案为:乙.
【点睛】
本题考查方差、中位数和众数:中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数),一般地设n个数据,x1,x2,…xn的平均数为,则方差S2= [(x1 )2+(x2 )2+…+(xn )2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
九年级数学第二学期第二十八章统计初步章节测试
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指 ( http: / / www.21cnjy.com )定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。21教育网
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、某县为了传承中华优秀传统文化,组 ( http: / / www.21cnjy.com )织了一次全县600名学生参加的“中华经典诵读”大赛.为了解本次大赛的选手成绩,随机抽取了其中50名选手的成绩进行统计分析.在这个问题中,下列说法中正确的是( )21*cnjy*com
A.这600名学生的“中华经典诵读”大赛成绩的全体是总体
B.50名学生是总体的一个样本
C.每个学生是个体
D.样本容量是50名
2、下列命题正确的是( )
A.数轴上的每一个点都表示一个有理数
B.甲、乙两人五次考试平均成绩相同,且,,则乙的成绩更稳定
C.三角形的一个外角大于任意一个内角
D.在平面直角坐标系中,点与点关于x轴对称
3、小明抛一枚硬币100次,其中有60次正面朝上,则反面朝上的频率是( )
A.0.6 B.6 C.0.4 D.4
4、某养羊场对200头生羊量进行统计, ( http: / / www.21cnjy.com )得到频数直方图(每一组含前一个边界值,不含后一个边界值)如图所示,其中质量在77.5kg及以上的生羊的只数是( )【出处:21教育名师】
( http: / / www.21cnjy.com / )
A.180 B.140 C.120 D.110
5、为了解甲、乙、丙、丁四位选手 ( http: / / www.21cnjy.com )射击水平,随机让四人各射击10次,计算四人10次射击命中环数平均数都是9.3环,方差(环2)如下表.则这四位选手成绩最稳定的是( )
选手 甲 乙 丙 丁
方差 0.035 0.016 0.022 0.025
A.甲 B.乙 C.丙 D.丁
6、在一次科技作品制作比赛中,某小组 ( http: / / www.21cnjy.com )八件作品的成绩(单位:分)分别是:7,10,9,8,7,9,9,8.对这组数据,下列说法正确的是( )2-1-c-n-j-y
A.平均数是8 B.众数是8.5 C.中位数8.5 D.极差是5
7、在一次班级体测调查中,收集到4 ( http: / / www.21cnjy.com )0名同学的跳高数据,数据分别落在5个组内,且落入第一、二、三、五组的数据个数分别为2、7、11、12,则第四组频数为( ).
A.9 B.8 C.7 D.6
8、下列问题不适合用全面调查的是( )
A.旅客上飞机前的安检 B.企业招聘,对应试人员进行面试
C.了解全班同学每周体育锻炼的时间 D.调查市场上某种食品的色素含量是否符合国家标准
9、八(3)班七个兴趣小组人数分别为4、4、5、、6、6、7,已知这组数据的平均数是5,则这组数据的中位数是( )
A.6 B.5 C.4 D.3
10、一个班有40名学生 ( http: / / www.21cnjy.com ),在一次身体素质测试中,将全班学生的测试结果分为优秀、合格、不合格.测试结果达到优秀的有18人,合格的有17人,则在这次测试中,测试结果不合格的频率是( )
A.0.125 B.0.30 C.0.45 D.1.25
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、某中学期中考试,八(1)班第一小组10人数学考试的成绩为:100分3人,90分5人,80分2人,则全组数学平均成绩为_____分.
2、小玲家的鱼塘里养了2 500条鲢鱼,按经 ( http: / / www.21cnjy.com )验,鲢鱼的成活率约为80%.现准备打捞出售,为了估计鱼塘中鲢鱼的总质量,从鱼塘中捕捞了3次进行统计,得到的数据如下表:
鱼的条数 平均每条鱼的质量
第一次捕捞 20
第二次捕捞 10
第三次捕捞 10
那么,鱼塘中鲢鱼的总质量约是________kg.
3、已知一组数据:18,17,13,15,17,16,14,17,则这组数据的中位数与众数分别是__________.
4、七年级(5)班20名女生的身高如下(单位:cm):
153 156 152 158 156 160 163 145 152 153
162 153 165 150 157 153 158 157 158 158
(1)请你在下表中填出身高在以下各个范围的频数,百分比(每个范围包含下限,但不包含上限):
身高(cm) 140~150 150~160 160~170
频数
百分比
(2)上表把身高分成___组,组距是___;
(3)身高在___范围的人数最多.
5、某同学对全班50名同学感兴趣的课外活动项目进行了调查,绘制下表:
活动项目 体育运动 学科兴趣小组 音乐 舞蹈 美术
人数(人) 15 12 10 5 8
(1)全班同学最感兴趣的课外活动项目是______;
(2)对音乐感兴趣的人数是____,占全班人数的百分比是_______.
三、解答题(5小题,每小题10分,共计50分)
1、山西某高校为了弘扬女排精神 ( http: / / www.21cnjy.com ),组建了女排社团,通过测量女同学的身高(单位:cm),并绘制了两幅不完整的统计图,请结合图中提供的信息,解答下列问题.21世纪教育网版权所有
( http: / / www.21cnjy.com / )
(1)填空:该排球社团一共有 名女同学,a= .
(2)把频数分布直方图补充完整.
(3)随机抽取1名学生,估计这名学生身高高于160cm的概率.
2、为了绿化环境,育英中学八年级三班同 ( http: / / www.21cnjy.com )学都积极参加植树活动,今年植树节时,该班同学植树情况的部分数据如图所示,请根据统计图信息,回答下列问题:【版权所有:21教育】
( http: / / www.21cnjy.com / ) ( http: / / www.21cnjy.com / )
(1)八年级三班共有多少名同学?
(2)条形统计图中,m=________,n=________.
(3)扇形统计图中,试计算植树2棵的人数所对应的扇形圆心角的度数.
3、为了解2路公共汽车的运营情况,公交部门统计了某天2路公共汽车每个运行班次的载客量,得到如表各项数据.
载客量/人 组中值 频数(班次)
1≤x<21 11 2
21≤x<41 a 8
41≤x<61 b 20
(1)求出表格中a=_______,b=______.
(2)计算该2路公共汽车平均每班的载客量是多少
4、某校七年级为了解学生课堂发言情况, ( http: / / www.21cnjy.com )随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下,并绘制了如图所示的两幅不完整的统计图,请结合图中相关数据回答下列问题:【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com / )
组别 发言次数n
A
B
C
D
E
F
(1)直接写出随机抽取学生的人数为______人;
(2)直接补全频数直方图;
(3)求扇形统计图中B部分所对应的百分比和F部分扇形圆心角的度数;
(4)该校七年级共有学生1000人,请估计七年级学生这天在课堂上发言次数大于等于12次的人数.
5、八(2)班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲 7 8 9 7 10 10 9 10 10 10
乙 10 8 7 9 8 10 10 9 10 9
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是 队.
-参考答案-
一、单选题
1、A
【分析】
根据总体的定义:表示考察的全体 ( http: / / www.21cnjy.com )对象;样本的定义:按照一定的抽样规则从总体中取出的一部分个体,样本中个体的数目称为样本容量;个体的定义:总体中每个成员成为个体,进行逐一判断即可.
【详解】
解:A、这600名学生的“中华经典诵读”大赛成绩的全体是总体,故本选项正确,符合题意;
B、50名学生的成绩是总体的一个样本,故本选项错误,不符合题意;
C、每个学生的成绩是个体,故本选项错误,不符合题意;
D、样本容量是50,故本选项错误,不符合题意;
故选A.
【点睛】
本题主要考查了样本,总体,个体和样本容量的定义,解题的关键在于熟知相关定义.
2、D
【分析】
根据数轴上的点与实数一一对应即可判断A;根据平均数相同的情形下,方差越小,成绩越稳定即可判断B;根据三角形的外角与内角的关系即可判断C;根据关于轴对称的点的坐标特征即可判断D
【详解】
A. 数轴上的每一个点都表示一个实数,故该选项不正确,不符合题意;
B. 甲、乙两人五次考试平均成绩相同,且,,则甲的成绩更稳定,故该选项不正确,不符合题意;
C. 三角形的一个外角不一定大于任意一个内角,故该选项不正确,不符合题意;
D. 在平面直角坐标系中,点与点关于x轴对称,故该选项正确,符合题意;
故选D
【点睛】
本题考查了实数与数轴,方差的意义,三角形的外角的性质,关于轴对称的点的坐标特征,掌握以上知识是解题的关键.2·1·c·n·j·y
3、C
【分析】
先求出反面朝上的频数,然后根据频率=频数÷总数求解即可
【详解】
解:∵小明抛一枚硬币100次,其中有60次正面朝上,
∴小明抛一枚硬币100次,其中有40次反面朝上,
∴反面朝上的频率=40÷100=0.4,
故选C.
【点睛】
本题主要考查了根据频数求频率,解题的关键在于能够熟练掌握频率=频数÷总数.
4、B
【分析】
根据题意和直方图中的数据可以求得质量在77.5kg及以上的生猪数,本题得以解决.
【详解】
解:由直方图可得,
质量在77.5kg及以上的生猪:90+30+20=140(头),
故选B.
【点睛】
本题考查频数分布直方图,解答本题的关键是明确题意,利用数形结合的思想解答.
5、B
【分析】
根据方差越小越稳定,比较后,选择即可.
【详解】
∵乙的方差最小,
∴乙最稳定,
故选B.
【点睛】
本题考查了方差的意义,正确理解方差越小越稳定是解题的关键.
6、C
【分析】
计算这组数据的平均数、众数、中位数及极差即可作出判断.
【详解】
这组数据的平均数为:,众数为9,中位数为8.5,极差为10-7=3,故正确的是中位数为8.5.
故选:C
【点睛】
本题考查了反映一组数据平均数、众数、中位数、极差等知识,正确计算这些统计量是关键.
7、B
【分析】
根据题意可得:共40个数据,知道一、二、三、五组的数据个数,用总数减去这几组频数,即可得到答案.
【详解】
解:由题意得:第四组的频数=40-(2+7+11+12)=8;
故选B.
【点睛】
本题是对频数的考查,掌握各小组频数之和等于数据总和是解题的关键.
8、D
【分析】
由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似,根据以上逐项分析可知.21·cn·jy·com
【详解】
解:A. 旅客上飞机前的安检,人员不多,且这个调查很重要不可漏掉任何人,适合全面调查,不符合题意, 21·世纪*教育网
B. 企业招聘,对应试人员进行面试,人员不多,且这个调查很重要不可漏掉任何人,适合全面调查,不符合题意,www-2-1-cnjy-com
C. 了解全班同学每周体育锻炼的时间,人员不多,适合全面调查,不符合题意,
D. 调查市场上某种食品的色素含量是否符合国家标准,调查具有破坏性,不适合全面调查,符合题意
故选D
【点睛】
本题考查的是全面调查与抽样调查, ( http: / / www.21cnjy.com )在调查实际生活中的相关问题时,要灵活处理,既要考虑问题本身的需要,又要考虑实现的可能性和所付出代价的大小.理解全面调查与抽样调查的适用范围是解题的关键.21教育名师原创作品
9、B
【分析】
本题可先算出x的值,再把数据按从小到大的顺序排列,找出最中间的数,即为中位数.
【详解】
解:∵某班七个兴趣小组人数分别为4,4,5,x,6,6,7.已知这组数据的平均数是5,
∴x=5×7 4 4 5 6 6 7=3,
∴这一组数从小到大排列为:3,4,4,5,6,6,7,
∴这组数据的中位数是:5.
故选:B.
【点睛】
本题考查的是中位数和平均数的定义,熟知中位数的定义是解答此题的关键.
10、A
【分析】
先求得不合格人数,再根据频率的计算公式求得不合格人数的频率即可.
【详解】
解:不合格人数为(人,
不合格人数的频率是,
故选:A.
【点睛】
本题主要考查了频率与概率,解题的关键是掌握频率是指每个对象出现的次数与总次数的比值(或者百分比).
二、填空题
1、91
【分析】
根据平均数公式计算.
【详解】
解:(分),
故答案为:91.
【点睛】
此题考查平均数的计算公式,熟记计算公式是解题的关键.
2、3600
【分析】
首先计算样本平均数,然后计算成活的鱼的数量,最后两个值相乘即可.
【详解】
解:每条鱼的平均重量为:千克,
成活的鱼的总数为:条,
则总质量约是千克.
故答案为:3600.
【点睛】
本题考查了利用样本估计总体,解题的关键是注意样本平均数的计算方法:总质量总条数,能够根据样本估算总体.21cnjy.com
3、16.5,17
【分析】
根据众数和中位数的定义求解即可,中 ( http: / / www.21cnjy.com )位数:将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数.如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.众数:在一组数据中出现次数最多的数.
【详解】
将,,,,,,,从小到大排列为:,,,,,,,
其中出现的次数最多,则众数为,
中位数为:.
故答案为:;
【点睛】
本题考查了求众数和中位数,理解众数和中位数的定义是解题的关键.
4、3
10 150~160
【分析】
(1)找出各个组中的人数,然后除以总人数即可得出所占百分比;
(2)通过所给的数据把各个范围中的人数填入相应表格,根据所填写的信息及题意确定分成的组数、组距;
(3)根据所填信息确定身高在哪个范围的人数最多即可.
【详解】
(1)填表:
身高(cm) 140~150 150~160 160~170
频数 1 15 4
百分比 5% 75% 20%
(2)上表把身高分成3组,组距是10;
(3)身高在范围最多.
【点睛】
本题考查的是从统计图表中获取信息,关键是找出各个组中的人数,通过所给的数据把各个范围中的人数填入相应表格,然后据此得出相关结论.www.21-cn-jy.com
5、体育运动 10
【分析】
(1)从统计表中直接通过比较即可得到.
(2)利用统计表,找到对音乐感兴趣的人数,再用对音乐感兴趣的人数除以全班人数,求出对应的百分比.
【详解】
解:从统计表分析人数可得到结论.由表可得:
(1)体育运动小组人数最多,所以全班同学最感兴趣的课外活动项目是体育运动;
(2)对音乐感兴趣的人数是10,占全班人数的百分比是10÷50=.
故答案为:(1)体育运动;(2)10,
【点睛】
本题主要是统计表的相关知识,如何读懂统计表,从统计表获取信息是关键.
三、解答题
1、(1)100,30;(2)见解析;(3)0.55
【分析】
(1)根据频数分布直方图中组的人数除以扇形统计图中组的所占百分比即可求得总人数,根据总人数减去组的人数即可求得组的人数,除以总人数即可求得的值;
(2)根据(1)中的结论补全统计图即可;
(3)根据身高高于160cm除以总人数即可求得随机抽取1名学生,估计这名学生身高高于160cm的概率【来源:21·世纪·教育·网】
【详解】
解:(1)总人数为:;
组的人数为
故答案为:
(2)如图,
( http: / / www.21cnjy.com / )
(3)总人数为,身高高于160cm为
随机抽取1名学生,估计这名学生身高高于160cm的概率为
【点睛】
本题考查了频数直方图和扇形统计图信息关联,简单概率计算,从统计图中获取信息是解题的关键.
2、
(1)50人;
(2) 10 7
(3)72°
【分析】
(1)根据植4株的有11人,所占百分比为,求出总人数;
(2)根据植树5棵人数所占的比例来求的值;用总人数减去其它植树的人数,就是的值,从而补全统计图;
(3)根据植树2棵的人数所占比例,即可得出圆心角的比例相同,即可求出圆心角的度数.
(1)
解:由两图可知,植树4棵的人数是11人,占全班人数的,所以八年级三班共有人数为:(人.
(2)
解:由扇形统计图可知,植树5棵人数占全班人数的,
所以(人.
(人.
故答案是:10;7;
(3)
解:所求扇形圆心角的度数为:
【点睛】
本题主要考查了扇形统计图的综合运用,解题的关键是读懂统计图,从不同的统计图中得到必要的信息,扇形统计图直接反映部分占总体的百分比大小.
3、(1)31;51;(2)43人.
【分析】
(1)利用组中值的计算方程直接计算即可得;
(2)利用组中值表示各组的平均数,然后根据加权平均数的计算方法求解即可.
【详解】
解:(1),
,
故答案为:31;51;
(2)(人),
答:该2路公共汽车平均每班的载客量是43人.
【点睛】
题目主要考查组中值及加权平均数的计算方法,理解题意,掌握组中值及加权平均数的计算方法是解题关键.
4、(1)50;(2)补全频数直方图见解析;(3)B部分所对应的百分比;F部分扇形圆心角的度数为;(4)180人.
【分析】
(1)用A组频数除以频率,即可求得抽取人数为50人;
(2)用50乘以C组所占百分比求出频数,用50减A、B、C、D、E组频数,即可求解,补全直方图即可;
(3)用B组频数除以50,即可求解;用F组频数除以50再乘以360°即可求解;
(4)用样本估计总体,用1000乘以样本中发言次数大于等于12的人数所占百分比,问题得解.
【详解】
(1)3÷6%=50,
故答案为:50;
(2)50×30%=15, 50-3-10-15-13-4=5,补全频数直方图如下;
( http: / / www.21cnjy.com / )
(3)B部分所对应的百分比,
F部分扇形圆心角的度数为;
(4)(人),
答:估计该校七年级学生1000人中,这天在课堂上发言次数大于等于12次的人数为180人.
【点睛】
本题考查了直方图,扇形图,用样本估计总体等知识,理解直方图、扇形图的意义,根据两种统计图中提供的公共信息求出样本容量是解题关键.
5、(1)9.5,10;(2)平均成绩9分,方差1;(3)乙
【分析】
(1)根据中位数的定义求出最中间两个数的平均数;根据众数的定义找出出现次数最多的数即可;
(2)先求出乙队的平均成绩,再根据方差公式进行计算;
(3)先比较出甲队和乙队的方差,再根据方差的意义即可得出答案.
【详解】
解:(1)把甲队的成绩从小 ( http: / / www.21cnjy.com )到大排列为:7,7,8,9,9,10,10,10,10,10,最中间两个数的平均数是(9+10)÷2=9.5(分),21*cnjy*com
则中位数是9.5分;
乙队成绩中10出现了4次,出现的次数最多,
则乙队成绩的众数是10分;
故答案为:9.5,10;
(2)乙队的平均成绩是:×(10×4+8×2+7+9×3)=9,
则方差是:×[4×(10﹣9)2+2×(8﹣9)2+(7﹣9)2+3×(9﹣9)2]=1;
(3)∵甲队成绩的方差是1.4,乙队成绩的方差是1,
∴成绩较为整齐的是乙队;
故答案为:乙.
【点睛】
本题考查方差、中位数和众数:中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数),一般地设n个数据,x1,x2,…xn的平均数为,则方差S2= [(x1 )2+(x2 )2+…+(xn )2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
