湘教版数学七年级上册 第3章 一元一次方程 本章真题训练(Word版含答案)
文档属性
| 名称 | 湘教版数学七年级上册 第3章 一元一次方程 本章真题训练(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 137.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-26 00:00:00 | ||
图片预览



文档简介
本章真题训练
一、选择题
1.[2021·毕节] 某商店换季准备打折出售某商品,如果按原售价的七五折出售,将亏损25元,而按原售价的九折出售,将盈利20元,则该商品的成本为 ( )
A.230元 B.250元 C.270元 D.300元
2.[2021·玉林] 观察下列按一定规律排列的n个数:2,4,6,8,10,12,…;若最后三个数之和是3000,则n等于 ( )
A.499 B.500 C.501 D.1002
3.[2021·金华] 如图,在编写数学谜题时,“□”内要求填写同一个数字,若设“□”内数字为x,则列出方程正确的是 ( )
A.3×2x+5=2x
B.3×20x+5=10x×2
C.3×20+x+5=20x
D.3×(20+x)+5=10x+2
4.[2021·恩施州] 定义运算“☆”:a☆b=a+b-1,例如:2☆3=2+3-1=4.若2☆x=1,则x的值是 ( )
A.-1 B.1 C.0 D.2
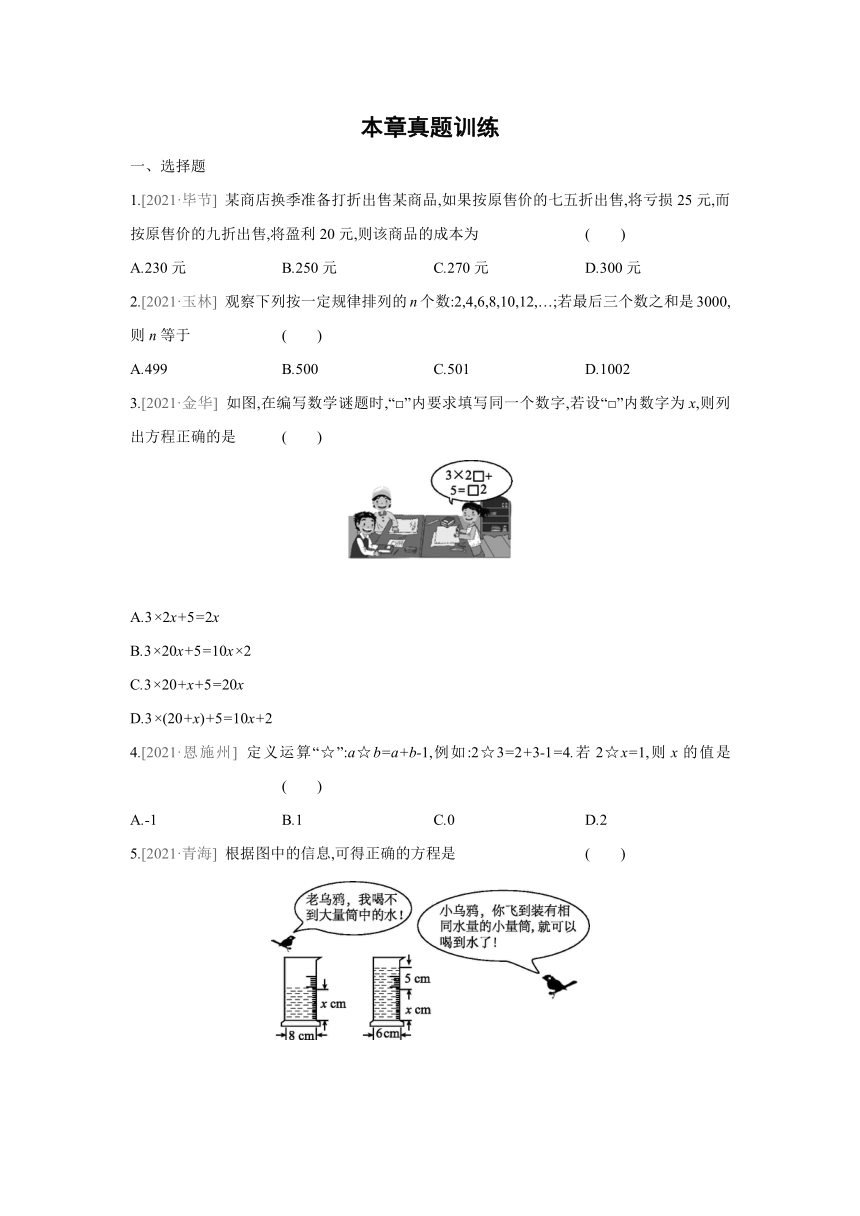
5.[2021·青海] 根据图中的信息,可得正确的方程是 ( )
A.π×2x=π×2×(x-5)
B.π×2x=π×2×(x+5)
C.π×82x=π×62×(x+5)
D.π×82x=π×62×5
6.[2021·东营] 中国古代数学著作《算法统宗》中有这样一段记载:“三百七十八里关,初日健步不为难,次日脚痛减一半,六朝才得到其关.”其大意是:有人要去某关口,路程378里,第一天健步行走,从第二天起,由于脚痛,每天走的路程都为前一天的一半,一共走了六天才到达目的地.则此人第三天走的路程为 ( )
A.96里 B.48里 C.24里 D.12里
二、填空题
7.[2021·衡阳] 某班有52名学生,其中男生人数比女生人数的2倍少17人,则女生有
名.
8.[2021·株洲] 方程3x-8=x的解为x= .
9.[2019·湘西州] 若关于x的方程3x-kx+2=0的解为x=2,则k的值为 .
10.[2021·常德] 新冠病毒疫情初期,口罩供应短缺.某地规定:每人每次限购5只.李红出门买口罩时,无论是否买到,都会消耗家里库存的口罩一只,如果有口罩买,她将买回5只.已知李红家原有库存15只,出门10次购买后,家里现有口罩35只.请问李红出门没有买到口罩的次数是
次.
11.[2021·长沙] 某数学老师在课外活动中做了一个有趣的游戏:首先发给A,B,C三个同学相同数量的扑克牌(假定发到每个同学手中的扑克牌数量足够多),然后依次完成下列三个步骤:
第一步,A同学拿出三张扑克牌给B同学;
第二步,C同学拿出三张扑克牌给B同学;
第三步,A同学手中此时有多少张扑克牌,B同学就拿出多少张扑克牌给A同学,请你确定,最终B同学手中剩余的扑克牌的张数为 .
三、解答题
12.[2021·凉山州] 解方程:x-=1-.
13.[2021·杭州] 以下是圆圆解方程-=1的解答过程.
解:去分母,得3(x+1)-2(x-3)=1.
去括号,得3x+1-2x+3=1.
移项、合并同类项,得x=-3.
圆圆的解答过程是否有错误 如果有错误,写出正确的解答过程.
14.[2021·娄底节选] 为了预防新冠肺炎疫情的发生,学校免费为师生提供防疫物品.某校花7200元购进洗手液与84消毒液共400瓶,已知洗手液的价格是25元/瓶,84消毒液的价格是15元/瓶.求该校购进洗手液和84消毒液各多少瓶.
15.[2019·烟台节选] 亚洲文明对话大会召开期间,大批的大学生志愿者参与服务工作.某大学计划组织本校全体志愿者统一乘车去会场,若单独调配36座新能源客车若干辆,则有2人没有座位;若只调配22座新能源客车,则用车数量将增加4辆,并空出2个座位.则计划调配36座新能源客车多少辆 该大学共有多少名志愿者
16.[2021·广州] 粤港澳大湾区自动驾驶产业联盟积极推进自动驾驶出租车应用落地工作,无人化是自动驾驶的终极目标.某公交集团拟在今明两年共投资9000万元改装260辆无人驾驶出租车投放市场.今年每辆无人驾驶出租车的改装费用是50万元,预计明年每辆无人驾驶出租车的改装费用可下降50%.
(1)求明年每辆无人驾驶出租车的预计改装费用是多少万元;
(2)求明年改装的无人驾驶出租车是多少辆.
17.[2019·盐城] 体育器材室有A,B两种型号的实心球,1个A型球与1个B型球的质量共7千克,3个A型球与1个B型球的质量共13千克.
(1)每个A型球、B型球的质量分别是多少千克
(2)现有A型球、B型球的质量共17千克,则A型球、B型球各有多少个
答案
1. B 设该商品的售价为x元.
由题意,得0.75x+25=0.9x-20,
解得x=300.
则成本价为300×0.75+25=250(元).
故选B.
2. C 设最后三个数为x-4,x-2,x.
由题意,得x-4+x-2+x=3000,
解得x=1002.
n=1002÷2=501.故选C.
3.[答案] D
4. C 由题意知:2☆x=2+x-1=1+x,
又2☆x=1,所以1+x=1,所以x=0.
故选C.
5. B 大量筒中的水的体积(单位:cm3)为π×2x,
小量筒中的水的体积(单位:cm3)为π×2×(x+5),
则可列方程为π×2x=π×2×(x+5).故选B.
6. B 设此人第一天走的路程为x里.
根据题意,得x+++++=378,
解得x=192.
所以此人第三天走的路程为==48.
故选B.
7.[答案] 23
8.[答案] 4
方程3x-8=x,
移项,得3x-x=8.
合并同类项,得2x=8,
系数化为1,得x=4.故答案为4.
9.[答案] 4
因为关于x的方程3x-kx+2=0的解为x=2,所以3×2-2k+2=0,解得k=4.
故答案为4.
10.[答案] 4
11.[答案] 9
设开始时每个同学手中扑克牌的数量都是x.
经过第一步后,A同学手中扑克牌的数量是x-3,B同学手中扑克牌的数量是x+3;
经过第二步后,B同学手中扑克牌的数量是x+3+3,C同学手中扑克牌的数量是x-3;
经过第三步后,A同学手中扑克牌的数量是2(x-3),B同学手中扑克牌的数量是x+3+3-(x-3);
所以B同学手中剩余的扑克牌的数量是x+3+3-(x-3)=9.故答案为9.
12.解:x-=1-.
去分母,得6x-3(x-2)=6-2(2x-1).
去括号,得6x-3x+6=6-4x+2.
移项,得6x-3x+4x=6-6+2.
合并同类项,得7x=2.
系数化为1,得x=.
13.解:圆圆的解答过程有错误.
正确的解答过程如下:
去分母,得3(x+1)-2(x-3)=6.
去括号,得3x+3-2x+6=6.
移项、合并同类项,得x=-3.
14.解:设该校购进洗手液x瓶,则购进84消毒液(400-x)瓶.
依题意,得25x+15(400-x)=7200,
解得x=120,400-x=280.
答:该校购进洗手液120瓶,购进84消毒液280瓶.
15.解:设计划调配36座新能源客车x辆.
根据题意,得36x+2=22(x+4)-2,解得x=6.
此时36x+2=218.
答:计划调配36座新能源客车6辆,该大学共有218名志愿者.
16.解:(1)依题意得50×(1-50%)=25(万元).
答:明年每辆无人驾驶出租车的预计改装费用是25万元.
(2)设明年改装的无人驾驶出租车是x辆,则今年改装的无人驾驶出租车是(260-x)辆.
依题意,得50×(260-x)+25x=9000,
解得x=160.
答:明年改装的无人驾驶出租车是160辆.
17.解:(1)设每个A型球的质量为x千克,则每个B型球的质量为(7-x)千克.根据题意,得3x+(7-x)=13,解得x=3,则7-x=4.
答:每个A型球的质量是3千克,每个B型球的质量是4千克.
(2)因为现有A型球、B型球的质量共17千克,所以设A型球1个,B型球a个,则3+4a=17,解得a=(不合题意,舍去);设A型球2个,B型球b个,则6+4b=17,解得b=(不合题意,舍去);设A型球3个,B型球c个,则9+4c=17,解得c=2;设A型球4个,B型球d个,则12+4d=17,解得d=(不合题意,舍去);设A型球5个,B型球e个,则15+4e=17,解得e=(不合题意,舍去).
综上,A型球有3个,B型球有2个.
一、选择题
1.[2021·毕节] 某商店换季准备打折出售某商品,如果按原售价的七五折出售,将亏损25元,而按原售价的九折出售,将盈利20元,则该商品的成本为 ( )
A.230元 B.250元 C.270元 D.300元
2.[2021·玉林] 观察下列按一定规律排列的n个数:2,4,6,8,10,12,…;若最后三个数之和是3000,则n等于 ( )
A.499 B.500 C.501 D.1002
3.[2021·金华] 如图,在编写数学谜题时,“□”内要求填写同一个数字,若设“□”内数字为x,则列出方程正确的是 ( )
A.3×2x+5=2x
B.3×20x+5=10x×2
C.3×20+x+5=20x
D.3×(20+x)+5=10x+2
4.[2021·恩施州] 定义运算“☆”:a☆b=a+b-1,例如:2☆3=2+3-1=4.若2☆x=1,则x的值是 ( )
A.-1 B.1 C.0 D.2
5.[2021·青海] 根据图中的信息,可得正确的方程是 ( )
A.π×2x=π×2×(x-5)
B.π×2x=π×2×(x+5)
C.π×82x=π×62×(x+5)
D.π×82x=π×62×5
6.[2021·东营] 中国古代数学著作《算法统宗》中有这样一段记载:“三百七十八里关,初日健步不为难,次日脚痛减一半,六朝才得到其关.”其大意是:有人要去某关口,路程378里,第一天健步行走,从第二天起,由于脚痛,每天走的路程都为前一天的一半,一共走了六天才到达目的地.则此人第三天走的路程为 ( )
A.96里 B.48里 C.24里 D.12里
二、填空题
7.[2021·衡阳] 某班有52名学生,其中男生人数比女生人数的2倍少17人,则女生有
名.
8.[2021·株洲] 方程3x-8=x的解为x= .
9.[2019·湘西州] 若关于x的方程3x-kx+2=0的解为x=2,则k的值为 .
10.[2021·常德] 新冠病毒疫情初期,口罩供应短缺.某地规定:每人每次限购5只.李红出门买口罩时,无论是否买到,都会消耗家里库存的口罩一只,如果有口罩买,她将买回5只.已知李红家原有库存15只,出门10次购买后,家里现有口罩35只.请问李红出门没有买到口罩的次数是
次.
11.[2021·长沙] 某数学老师在课外活动中做了一个有趣的游戏:首先发给A,B,C三个同学相同数量的扑克牌(假定发到每个同学手中的扑克牌数量足够多),然后依次完成下列三个步骤:
第一步,A同学拿出三张扑克牌给B同学;
第二步,C同学拿出三张扑克牌给B同学;
第三步,A同学手中此时有多少张扑克牌,B同学就拿出多少张扑克牌给A同学,请你确定,最终B同学手中剩余的扑克牌的张数为 .
三、解答题
12.[2021·凉山州] 解方程:x-=1-.
13.[2021·杭州] 以下是圆圆解方程-=1的解答过程.
解:去分母,得3(x+1)-2(x-3)=1.
去括号,得3x+1-2x+3=1.
移项、合并同类项,得x=-3.
圆圆的解答过程是否有错误 如果有错误,写出正确的解答过程.
14.[2021·娄底节选] 为了预防新冠肺炎疫情的发生,学校免费为师生提供防疫物品.某校花7200元购进洗手液与84消毒液共400瓶,已知洗手液的价格是25元/瓶,84消毒液的价格是15元/瓶.求该校购进洗手液和84消毒液各多少瓶.
15.[2019·烟台节选] 亚洲文明对话大会召开期间,大批的大学生志愿者参与服务工作.某大学计划组织本校全体志愿者统一乘车去会场,若单独调配36座新能源客车若干辆,则有2人没有座位;若只调配22座新能源客车,则用车数量将增加4辆,并空出2个座位.则计划调配36座新能源客车多少辆 该大学共有多少名志愿者
16.[2021·广州] 粤港澳大湾区自动驾驶产业联盟积极推进自动驾驶出租车应用落地工作,无人化是自动驾驶的终极目标.某公交集团拟在今明两年共投资9000万元改装260辆无人驾驶出租车投放市场.今年每辆无人驾驶出租车的改装费用是50万元,预计明年每辆无人驾驶出租车的改装费用可下降50%.
(1)求明年每辆无人驾驶出租车的预计改装费用是多少万元;
(2)求明年改装的无人驾驶出租车是多少辆.
17.[2019·盐城] 体育器材室有A,B两种型号的实心球,1个A型球与1个B型球的质量共7千克,3个A型球与1个B型球的质量共13千克.
(1)每个A型球、B型球的质量分别是多少千克
(2)现有A型球、B型球的质量共17千克,则A型球、B型球各有多少个
答案
1. B 设该商品的售价为x元.
由题意,得0.75x+25=0.9x-20,
解得x=300.
则成本价为300×0.75+25=250(元).
故选B.
2. C 设最后三个数为x-4,x-2,x.
由题意,得x-4+x-2+x=3000,
解得x=1002.
n=1002÷2=501.故选C.
3.[答案] D
4. C 由题意知:2☆x=2+x-1=1+x,
又2☆x=1,所以1+x=1,所以x=0.
故选C.
5. B 大量筒中的水的体积(单位:cm3)为π×2x,
小量筒中的水的体积(单位:cm3)为π×2×(x+5),
则可列方程为π×2x=π×2×(x+5).故选B.
6. B 设此人第一天走的路程为x里.
根据题意,得x+++++=378,
解得x=192.
所以此人第三天走的路程为==48.
故选B.
7.[答案] 23
8.[答案] 4
方程3x-8=x,
移项,得3x-x=8.
合并同类项,得2x=8,
系数化为1,得x=4.故答案为4.
9.[答案] 4
因为关于x的方程3x-kx+2=0的解为x=2,所以3×2-2k+2=0,解得k=4.
故答案为4.
10.[答案] 4
11.[答案] 9
设开始时每个同学手中扑克牌的数量都是x.
经过第一步后,A同学手中扑克牌的数量是x-3,B同学手中扑克牌的数量是x+3;
经过第二步后,B同学手中扑克牌的数量是x+3+3,C同学手中扑克牌的数量是x-3;
经过第三步后,A同学手中扑克牌的数量是2(x-3),B同学手中扑克牌的数量是x+3+3-(x-3);
所以B同学手中剩余的扑克牌的数量是x+3+3-(x-3)=9.故答案为9.
12.解:x-=1-.
去分母,得6x-3(x-2)=6-2(2x-1).
去括号,得6x-3x+6=6-4x+2.
移项,得6x-3x+4x=6-6+2.
合并同类项,得7x=2.
系数化为1,得x=.
13.解:圆圆的解答过程有错误.
正确的解答过程如下:
去分母,得3(x+1)-2(x-3)=6.
去括号,得3x+3-2x+6=6.
移项、合并同类项,得x=-3.
14.解:设该校购进洗手液x瓶,则购进84消毒液(400-x)瓶.
依题意,得25x+15(400-x)=7200,
解得x=120,400-x=280.
答:该校购进洗手液120瓶,购进84消毒液280瓶.
15.解:设计划调配36座新能源客车x辆.
根据题意,得36x+2=22(x+4)-2,解得x=6.
此时36x+2=218.
答:计划调配36座新能源客车6辆,该大学共有218名志愿者.
16.解:(1)依题意得50×(1-50%)=25(万元).
答:明年每辆无人驾驶出租车的预计改装费用是25万元.
(2)设明年改装的无人驾驶出租车是x辆,则今年改装的无人驾驶出租车是(260-x)辆.
依题意,得50×(260-x)+25x=9000,
解得x=160.
答:明年改装的无人驾驶出租车是160辆.
17.解:(1)设每个A型球的质量为x千克,则每个B型球的质量为(7-x)千克.根据题意,得3x+(7-x)=13,解得x=3,则7-x=4.
答:每个A型球的质量是3千克,每个B型球的质量是4千克.
(2)因为现有A型球、B型球的质量共17千克,所以设A型球1个,B型球a个,则3+4a=17,解得a=(不合题意,舍去);设A型球2个,B型球b个,则6+4b=17,解得b=(不合题意,舍去);设A型球3个,B型球c个,则9+4c=17,解得c=2;设A型球4个,B型球d个,则12+4d=17,解得d=(不合题意,舍去);设A型球5个,B型球e个,则15+4e=17,解得e=(不合题意,舍去).
综上,A型球有3个,B型球有2个.
同课章节目录
