人教版八年级上册14.2.2 完全平方公式 课件 (共19张PPT)
文档属性
| 名称 | 人教版八年级上册14.2.2 完全平方公式 课件 (共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 280.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-25 10:41:57 | ||
图片预览




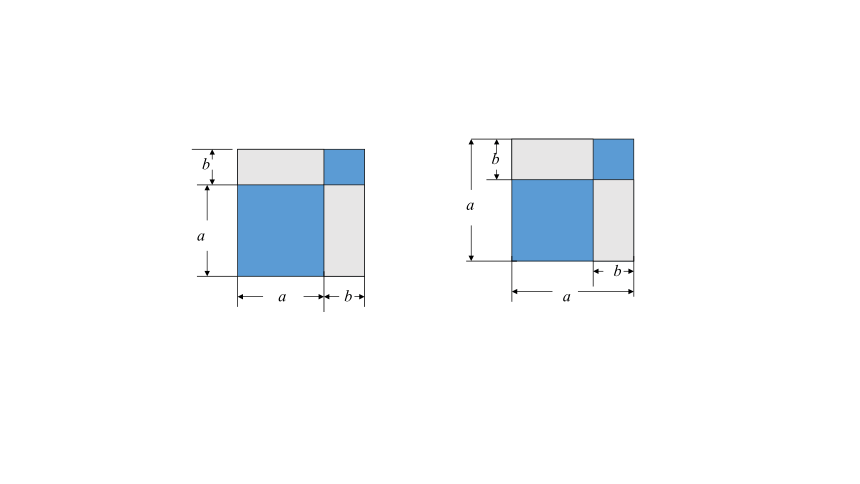
文档简介
(共19张PPT)
14.2.2 完全平方公式
人教版数学八年级上册
请大家根据自己拼成的正方形尝试解决以下四个问题:
(1)试用不同形式表示新正方形的面积,并进行比较,你发现了什么?
(2)你能用多项式乘法法则来验证你的发现吗?
(3)试着用自己的语言叙述你发现的式子
(4)根据上述等式的结构特点,你能想出巧妙的方法记着这个式子吗?试试看
想
一
想
b
a
b
a
b
a
b
a
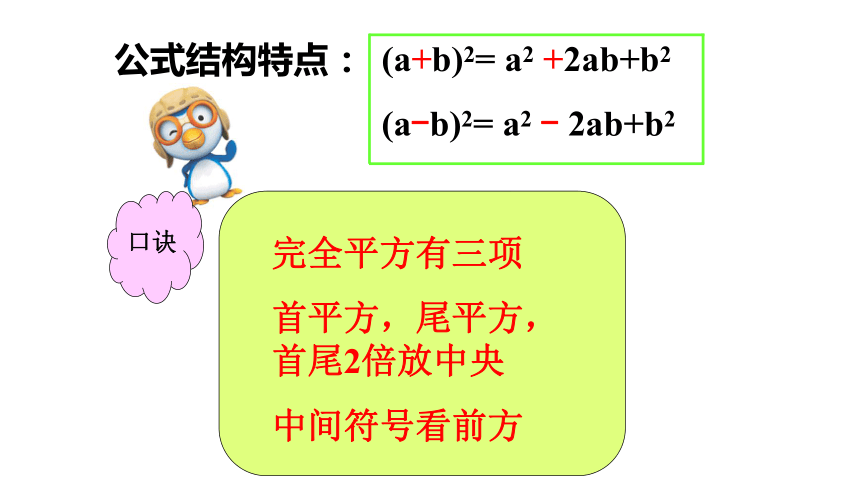
公式结构特点:
4.公式中的字母a,b可以表示数,单项式和多项式。
1.积为二次三项式;
2.积中两项为两数的平方和;
3.另一项是两数积的2倍,
且与前面的符号相同。
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
完全平方有三项
首平方,尾平方,
首尾2倍放中央
中间符号看前方
口诀
下面各式的计算是否正确?如果不正确,应当怎样改正?
(1)(x -y)2 =x2 -y2
(3)(-x+y)2 =x2+2xy +y2
辩
一
辩
(2)(x +3)2 =x2 +3x+9
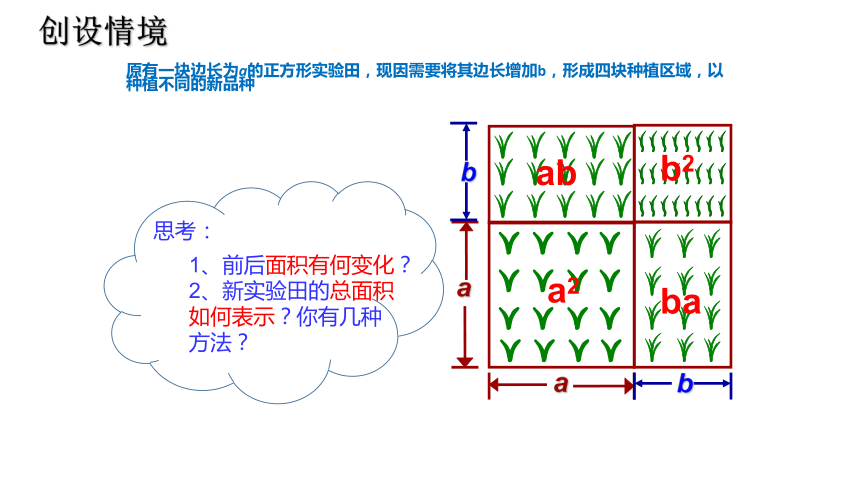
原有一块边长为a的正方形实验田,现因需要将其边长增加b,形成四块种植区域,以种植不同的新品种
a
a
b
b
创设情境
思考:
1、前后面积有何变化?
2、新实验田的总面积如何表示?你有几种方法?
a2
ab
ba
b2
两种形式表达实验田的面积
1、整体看
新试验田的边长为(a+b)的正方形,面积为(a+b)2
2、部分看
(1)四块面积分别为a2、b2、ab、ba
(2)四块面积的和为a2+2ab+b2
(a+b)2
a2+2ab+b2
=
b
a
a
b
b
a
b
a
(1) 你能用多项式的乘法法则来说明它成立吗
(a+b)2=a2+2ab+b2 ;
(a+b)
(a+b)
=a2+ab+
ab+b2
=a2+2ab+
b2;
(a b)2=
合作交流
你能根据图中的变化说明阴影的面积吗
思考:
b
a
b
a
(a b)2
=
(a b)2
(a+b)2
=a2+2ab+b2
(a-b)2
=a2-2ab+b2
完全平方公式
观察这两个公式的特征:
1、这两个公式有什么相同点和不同点?
2、你能用语言叙述这两个公式吗?
语言描述:
两数和 的平方,等于这两数的平方和,加上 这两数的积的2倍。
(或减去)
(或差)
注意:a、b不仅代表数字,也可代表式子。
例1、运用完全平方公式计算:
解: (-4m+n)2=
=16m2
(1)(n-4m)2
(a +b)2= a2 + 2 a b + b2
(-4m)2
+2 (-4m) n
+n2
-8mn
+n2
记忆口诀:首平方、尾平方,2倍乘积在中央,中央符号看前方(同号得正、异号得负)
(1)(-4m+n)2
=n2
(4m)2
2 4m n
+
-
=16m2
-8mn
+n2
(1) 1022
解: 1022
= (100+2)2
=10000+400+4
=10404
(2) 992
解: 992
= (100 –1)2
=10000 -200+1
=9801
例2、运用完全平方公式计算:
1.运用完全平方公式计算:
(1)(x+6)2; (2) (y-5)2;
(3) (-2x+5)2; (4) ( x - y)2.
2.运用完全平方公式计算:
(1) 9.9; (2)201.
基础练习:
思考
(a+b)2与(-a-b)2相等吗
(a-b)2与(b-a)2相等吗
(a-b)2与a2-b2相等吗
为什么
运用完全平方公式计算
(1) (4m+n)2 (2)(y - )2
(3) ( -x + 2y)2
挑战自我:
(a ± b)2 = a2± 2ab + b2
(4) 1022
(1) (-3x+2)(-3x-2)
(2) (-a-b)2
(3) (5x+2)(-5x+2)
(4) ( 3a + b)(-3a - b)
下面式子能用完全平方公式吗?
想一想
有一边长为a米的正方形桌子,现准备铺上正方形桌布,桌布四周均超出桌面0.1米,问需要多大面积的桌布?
(a+0.2)2 =a2 +0.4a+0.04
帮妈妈买桌布:
蓦然回首:
1.本节课你学习了什么?
2.用什么方法获得其结论的?
3.你印象最深的数学方法是什么?
4.你曾经在哪些问题上有错误认识?得到纠正了吗?
谢谢大家!
14.2.2 完全平方公式
人教版数学八年级上册
请大家根据自己拼成的正方形尝试解决以下四个问题:
(1)试用不同形式表示新正方形的面积,并进行比较,你发现了什么?
(2)你能用多项式乘法法则来验证你的发现吗?
(3)试着用自己的语言叙述你发现的式子
(4)根据上述等式的结构特点,你能想出巧妙的方法记着这个式子吗?试试看
想
一
想
b
a
b
a
b
a
b
a
公式结构特点:
4.公式中的字母a,b可以表示数,单项式和多项式。
1.积为二次三项式;
2.积中两项为两数的平方和;
3.另一项是两数积的2倍,
且与前面的符号相同。
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
完全平方有三项
首平方,尾平方,
首尾2倍放中央
中间符号看前方
口诀
下面各式的计算是否正确?如果不正确,应当怎样改正?
(1)(x -y)2 =x2 -y2
(3)(-x+y)2 =x2+2xy +y2
辩
一
辩
(2)(x +3)2 =x2 +3x+9
原有一块边长为a的正方形实验田,现因需要将其边长增加b,形成四块种植区域,以种植不同的新品种
a
a
b
b
创设情境
思考:
1、前后面积有何变化?
2、新实验田的总面积如何表示?你有几种方法?
a2
ab
ba
b2
两种形式表达实验田的面积
1、整体看
新试验田的边长为(a+b)的正方形,面积为(a+b)2
2、部分看
(1)四块面积分别为a2、b2、ab、ba
(2)四块面积的和为a2+2ab+b2
(a+b)2
a2+2ab+b2
=
b
a
a
b
b
a
b
a
(1) 你能用多项式的乘法法则来说明它成立吗
(a+b)2=a2+2ab+b2 ;
(a+b)
(a+b)
=a2+ab+
ab+b2
=a2+2ab+
b2;
(a b)2=
合作交流
你能根据图中的变化说明阴影的面积吗
思考:
b
a
b
a
(a b)2
=
(a b)2
(a+b)2
=a2+2ab+b2
(a-b)2
=a2-2ab+b2
完全平方公式
观察这两个公式的特征:
1、这两个公式有什么相同点和不同点?
2、你能用语言叙述这两个公式吗?
语言描述:
两数和 的平方,等于这两数的平方和,加上 这两数的积的2倍。
(或减去)
(或差)
注意:a、b不仅代表数字,也可代表式子。
例1、运用完全平方公式计算:
解: (-4m+n)2=
=16m2
(1)(n-4m)2
(a +b)2= a2 + 2 a b + b2
(-4m)2
+2 (-4m) n
+n2
-8mn
+n2
记忆口诀:首平方、尾平方,2倍乘积在中央,中央符号看前方(同号得正、异号得负)
(1)(-4m+n)2
=n2
(4m)2
2 4m n
+
-
=16m2
-8mn
+n2
(1) 1022
解: 1022
= (100+2)2
=10000+400+4
=10404
(2) 992
解: 992
= (100 –1)2
=10000 -200+1
=9801
例2、运用完全平方公式计算:
1.运用完全平方公式计算:
(1)(x+6)2; (2) (y-5)2;
(3) (-2x+5)2; (4) ( x - y)2.
2.运用完全平方公式计算:
(1) 9.9; (2)201.
基础练习:
思考
(a+b)2与(-a-b)2相等吗
(a-b)2与(b-a)2相等吗
(a-b)2与a2-b2相等吗
为什么
运用完全平方公式计算
(1) (4m+n)2 (2)(y - )2
(3) ( -x + 2y)2
挑战自我:
(a ± b)2 = a2± 2ab + b2
(4) 1022
(1) (-3x+2)(-3x-2)
(2) (-a-b)2
(3) (5x+2)(-5x+2)
(4) ( 3a + b)(-3a - b)
下面式子能用完全平方公式吗?
想一想
有一边长为a米的正方形桌子,现准备铺上正方形桌布,桌布四周均超出桌面0.1米,问需要多大面积的桌布?
(a+0.2)2 =a2 +0.4a+0.04
帮妈妈买桌布:
蓦然回首:
1.本节课你学习了什么?
2.用什么方法获得其结论的?
3.你印象最深的数学方法是什么?
4.你曾经在哪些问题上有错误认识?得到纠正了吗?
谢谢大家!
