湘教版数学九年级上册第3章 图形的相似 单元综合测试(word版含答案)
文档属性
| 名称 | 湘教版数学九年级上册第3章 图形的相似 单元综合测试(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 412.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-26 00:00:00 | ||
图片预览



文档简介
第3章 图形的相似 单元综合测试
一、选择题(本大题共7小题,每小题4分,共28分)
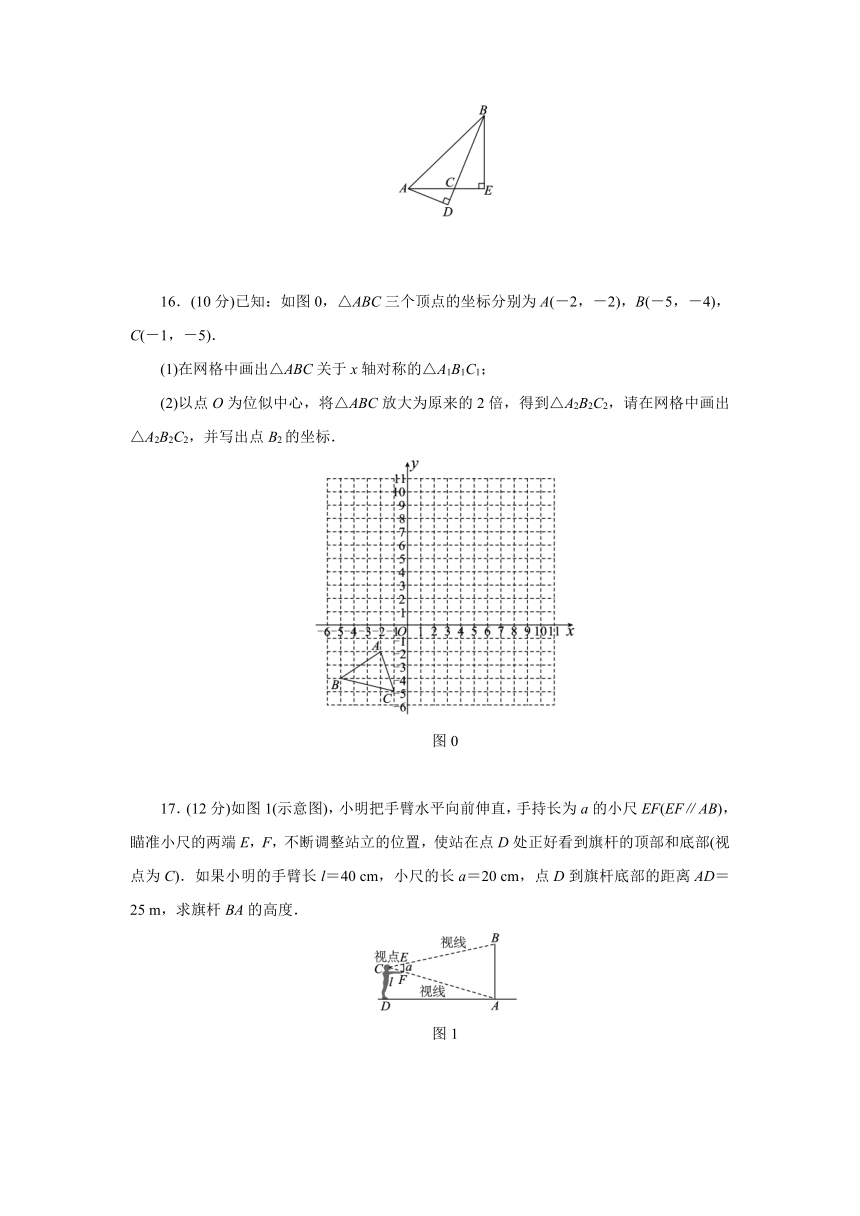
1.以下列数据为长度的线段中,能成比例的是( )
A.3 cm,6 cm,8 cm,9 cm
B.3 cm,5 cm,6 cm,9 cm
C.3 cm,6 cm,7 cm,9 cm
D.3 cm,6 cm,9 cm,18 cm
2.已知△FHB∽△EAD,它们的周长分别为30和15,且FH=6,则EA的长为( )
A.3 B.2 C.4 D.5
3.在△ABC中,D,E分别为边AB,AC的中点,则△ADE与△ABC的面积之比为( )
A. B. C. D.
4.在△ABC和△DEF中,AB=AC,DE=DF,根据下列条件,能判定△ABC和△DEF相似的是( )
A.= B.=
C.∠A=∠E D.∠B=∠D
5.宽与长的比是(约0.618)的矩形叫作黄金矩形,黄金矩形蕴藏着丰富的美学价值,给我们以协调和匀称的美感.我们可以用这样的方法画出黄金矩形:如图,作正方形ABCD,分别取AD,BC的中点E,F,连接EF.以F为圆心,FD的长为半径画弧,交BC的延长线于点G.作GH⊥AD,交AD的延长线于点H,则下列矩形是黄金矩形的是( )
A.矩形ABFE B.矩形EFCD
C.矩形EFGH D.矩形DCGH
6.如图,已知△ABC,任取一点O,连接AO,BO,CO,并取它们的中点D,E,F,得到△DEF,则下列说法正确的个数是( )
①△ABC与△DEF是位似图形;②△ABC与△DEF是相似图形;③△ABC与△DEF的周长比为1∶2;④△ABC与△DEF的面积比为4∶1.
A.1 B.2
C.3 D.4
7.如图所示,某校数学兴趣小组利用标杆BE测量建筑物的高度(其中点A,E,D共线,点A,B,C共线),已知标杆BE高1.5 m,测得AB=1.2 m,BC=12.8 m,则建筑物CD的高度是( )
A.17.5 m B.17 m
C.16.5 m D.18 m
二、填空题(本大题共7小题,每小题4分,共28分)
8.已知=3,则=________.
9.在△ABC中,AB=6,AC=8,在△DEF中,DE=4,DF=3,要使△ABC与△DEF相似,需添加一个条件是____________.(写出一种情况即可)
10.如图,四边形ABCD与四边形A′B′C′D′位似,位似中心为点O,OC=6,CC′=4,AB=3,则A′B′=________.
11.如图,在△ABC中,D为AB边上一点,且∠BCD=∠A.若BC=2 ,AB=3,则BD=________.
12.如图,在平面直角坐标系中,将△AOB以点O为位似中心,为位似比作位似变换,得到△A1OB1.已知A(2,3),则点A1的坐标是________.
13.如图,为了测量一水塔的高度,小强用2 m长的竹竿做测量工具,移动竹竿,使竹竿、水塔顶端的影子恰好落在地面上的同一点.此时,竹竿与这一点相距8 m,与水塔相距32 m,则水塔的高度为________m.
14.在每个小正方形的边长均为1的网格图形中,每个小正方形的顶点称为格点,顶点都是格点的三角形称为格点三角形.如图,已知Rt△ABC是6×6网格图形中的格点三角形,则该图中所有与Rt△ABC相似的格点三角形中.面积最大的三角形的斜边长是________.
三、解答题(本大题共4小题,共44分)
15.(10分)如图所示,AD,BE分别是钝角三角形ABC的边BC,AC上的高.求证:=.
16.(10分)已知:如图0,△ABC三个顶点的坐标分别为A(-2,-2),B(-5,-4),C(-1,-5).
(1)在网格中画出△ABC关于x轴对称的△A1B1C1;
(2)以点O为位似中心,将△ABC放大为原来的2倍,得到△A2B2C2,请在网格中画出△A2B2C2,并写出点B2的坐标.
图0
17.(12分)如图1(示意图),小明把手臂水平向前伸直,手持长为a的小尺EF(EF∥AB),瞄准小尺的两端E,F,不断调整站立的位置,使站在点D处正好看到旗杆的顶部和底部(视点为C).如果小明的手臂长l=40 cm,小尺的长a=20 cm,点D到旗杆底部的距离AD=25 m,求旗杆BA的高度.
图1
18.(12分)如图2,在 ABCD中,DE⊥AC于点O,交BC于点E,EG=EC,GF∥AD交DE于点F,连接FC,H为线段AO上一点,连接HD,HF.
(1)判断四边形GECF的形状,并说明理由;
(2)当∠DHF=∠HAD时,求证:AH·CH=EC·AD.
图2
答案
1.[答案] D
2. A ∵△FHB和△EAD的周长分别为30和15,
∴△FHB和△EAD的周长比为2∶1.
∵△FHB∽△EAD,
∴=2,即=2,解得EA=3.
3.[答案] C
4.[答案] B
5. D 设正方形ABCD的边长为2,则CD=2,CF=1.在Rt△DCF中,DF===,∴FG=,
∴CG=-1,
∴=,
∴矩形DCGH为黄金矩形.故选D.
6. C 根据位似的性质得出①△ABC与△DEF是位似图形,②△ABC与△DEF是相似图形.∵△DEF是将△ABC的三边缩小为原来的得到的,∴△ABC与△DEF的周长比为2∶1,故③错误.根据面积比等于相似比的平方,可知④△ABC与△DEF的面积比为4∶1.故选C.
7. A ∵AB=1.2 m,BC=12.8 m,
∴AC=1.2+12.8=14(m).
∵标杆BE和建筑物CD均垂直于地面,
∴BE∥CD,∴△ABE∽△ACD,
∴=,
即=,解得CD=17.5(m).
故选A.
8.[答案] 2
9.[答案] ∠A=∠D(答案不唯一)
10.[答案] 5
∵四边形ABCD与四边形A′B′C′D′位似,其位似中心为点O,OC=6,CC′=4,
∴==,
∴=.
又∵AB=3,∴A′B′=5.
11.[答案]
易得△BCD∽△BAC,从而BC∶BA=BD∶BC,代入求得BD=.
12.[答案] (,2)
∵将△AOB以点O为位似中心,为位似比作位似变换,得到△A1OB1,A(2,3),∴点A1的坐标是(×2,×3),即A1(,2).故答案为(,2).
13.[答案] 10
14.[答案] 5
∵在Rt△ABC中,AC=1,BC=2,
∴AB=,AC∶BC=1∶2,
∴与Rt△ABC相似的格点三角形的两直角边的比值为1∶2.
若该三角形最短边长为4,则另一直角边长为8,但在6×6网格图形中,最长线段为6 ,但此时画出的直角三角形为等腰直角三角形,从而画不出端点都在格点且长为8的线段,故最短直角边长应小于4,在图中尝试,可画出DE=,EF=2 ,DF=5 的三角形,
∵===,
∴△ABC∽△DFE,
∴∠DEF=∠C=90°,
∴此时△DEF的面积为×2 ÷2=10,△DEF为所求面积最大的三角形,其斜边长为5 .
15.证明:∵AD,BE是钝角三角形ABC的高,
∴∠ADC=∠BEC=90°.
又∵∠DCA=∠BCE,
∴△DAC∽△EBC,
∴=.
16.解:(1)(2)画图如下图所示,B2(10,8).
17.解:过点C作CH⊥AB于点H,交EF于点P,则CH=AD=25 m,CP=40 cm=0.4 m,EF=20 cm=0.2 m.
由题意,得EF∥AB,
∴△CEF∽△CBA,
∴=,即=,
解得BA=12.5(m).
答:旗杆BA的高度为12.5 m.
18.解:(1)四边形GECF是菱形.理由:
∵EG=EC,DE⊥AC,
∴GO=CO.
∵GF∥AD,AD∥BC,
∴GF∥BC,
∴∠FGO=∠ECO,∠GFO=∠CEO,
∴△GFO≌△CEO(AAS),
∴GF=EC.
又∵GF∥EC,
∴四边形GECF是平行四边形.
又∵EG=EC,
∴四边形GECF是菱形.
(2)证明:∵∠DHC=∠DAH+∠ADH=∠DHF+∠FHC,∠DHF=∠HAD,
∴∠ADH=∠FHC.
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAH=∠ACB.
∵四边形GECF是菱形,
∴CE=CF,∠HCF=∠ACB,
∴∠HCF=∠DAH,
∴△ADH∽△CHF,
则=.
又∵CF=EC,∴AH·CH=EC·AD.
一、选择题(本大题共7小题,每小题4分,共28分)
1.以下列数据为长度的线段中,能成比例的是( )
A.3 cm,6 cm,8 cm,9 cm
B.3 cm,5 cm,6 cm,9 cm
C.3 cm,6 cm,7 cm,9 cm
D.3 cm,6 cm,9 cm,18 cm
2.已知△FHB∽△EAD,它们的周长分别为30和15,且FH=6,则EA的长为( )
A.3 B.2 C.4 D.5
3.在△ABC中,D,E分别为边AB,AC的中点,则△ADE与△ABC的面积之比为( )
A. B. C. D.
4.在△ABC和△DEF中,AB=AC,DE=DF,根据下列条件,能判定△ABC和△DEF相似的是( )
A.= B.=
C.∠A=∠E D.∠B=∠D
5.宽与长的比是(约0.618)的矩形叫作黄金矩形,黄金矩形蕴藏着丰富的美学价值,给我们以协调和匀称的美感.我们可以用这样的方法画出黄金矩形:如图,作正方形ABCD,分别取AD,BC的中点E,F,连接EF.以F为圆心,FD的长为半径画弧,交BC的延长线于点G.作GH⊥AD,交AD的延长线于点H,则下列矩形是黄金矩形的是( )
A.矩形ABFE B.矩形EFCD
C.矩形EFGH D.矩形DCGH
6.如图,已知△ABC,任取一点O,连接AO,BO,CO,并取它们的中点D,E,F,得到△DEF,则下列说法正确的个数是( )
①△ABC与△DEF是位似图形;②△ABC与△DEF是相似图形;③△ABC与△DEF的周长比为1∶2;④△ABC与△DEF的面积比为4∶1.
A.1 B.2
C.3 D.4
7.如图所示,某校数学兴趣小组利用标杆BE测量建筑物的高度(其中点A,E,D共线,点A,B,C共线),已知标杆BE高1.5 m,测得AB=1.2 m,BC=12.8 m,则建筑物CD的高度是( )
A.17.5 m B.17 m
C.16.5 m D.18 m
二、填空题(本大题共7小题,每小题4分,共28分)
8.已知=3,则=________.
9.在△ABC中,AB=6,AC=8,在△DEF中,DE=4,DF=3,要使△ABC与△DEF相似,需添加一个条件是____________.(写出一种情况即可)
10.如图,四边形ABCD与四边形A′B′C′D′位似,位似中心为点O,OC=6,CC′=4,AB=3,则A′B′=________.
11.如图,在△ABC中,D为AB边上一点,且∠BCD=∠A.若BC=2 ,AB=3,则BD=________.
12.如图,在平面直角坐标系中,将△AOB以点O为位似中心,为位似比作位似变换,得到△A1OB1.已知A(2,3),则点A1的坐标是________.
13.如图,为了测量一水塔的高度,小强用2 m长的竹竿做测量工具,移动竹竿,使竹竿、水塔顶端的影子恰好落在地面上的同一点.此时,竹竿与这一点相距8 m,与水塔相距32 m,则水塔的高度为________m.
14.在每个小正方形的边长均为1的网格图形中,每个小正方形的顶点称为格点,顶点都是格点的三角形称为格点三角形.如图,已知Rt△ABC是6×6网格图形中的格点三角形,则该图中所有与Rt△ABC相似的格点三角形中.面积最大的三角形的斜边长是________.
三、解答题(本大题共4小题,共44分)
15.(10分)如图所示,AD,BE分别是钝角三角形ABC的边BC,AC上的高.求证:=.
16.(10分)已知:如图0,△ABC三个顶点的坐标分别为A(-2,-2),B(-5,-4),C(-1,-5).
(1)在网格中画出△ABC关于x轴对称的△A1B1C1;
(2)以点O为位似中心,将△ABC放大为原来的2倍,得到△A2B2C2,请在网格中画出△A2B2C2,并写出点B2的坐标.
图0
17.(12分)如图1(示意图),小明把手臂水平向前伸直,手持长为a的小尺EF(EF∥AB),瞄准小尺的两端E,F,不断调整站立的位置,使站在点D处正好看到旗杆的顶部和底部(视点为C).如果小明的手臂长l=40 cm,小尺的长a=20 cm,点D到旗杆底部的距离AD=25 m,求旗杆BA的高度.
图1
18.(12分)如图2,在 ABCD中,DE⊥AC于点O,交BC于点E,EG=EC,GF∥AD交DE于点F,连接FC,H为线段AO上一点,连接HD,HF.
(1)判断四边形GECF的形状,并说明理由;
(2)当∠DHF=∠HAD时,求证:AH·CH=EC·AD.
图2
答案
1.[答案] D
2. A ∵△FHB和△EAD的周长分别为30和15,
∴△FHB和△EAD的周长比为2∶1.
∵△FHB∽△EAD,
∴=2,即=2,解得EA=3.
3.[答案] C
4.[答案] B
5. D 设正方形ABCD的边长为2,则CD=2,CF=1.在Rt△DCF中,DF===,∴FG=,
∴CG=-1,
∴=,
∴矩形DCGH为黄金矩形.故选D.
6. C 根据位似的性质得出①△ABC与△DEF是位似图形,②△ABC与△DEF是相似图形.∵△DEF是将△ABC的三边缩小为原来的得到的,∴△ABC与△DEF的周长比为2∶1,故③错误.根据面积比等于相似比的平方,可知④△ABC与△DEF的面积比为4∶1.故选C.
7. A ∵AB=1.2 m,BC=12.8 m,
∴AC=1.2+12.8=14(m).
∵标杆BE和建筑物CD均垂直于地面,
∴BE∥CD,∴△ABE∽△ACD,
∴=,
即=,解得CD=17.5(m).
故选A.
8.[答案] 2
9.[答案] ∠A=∠D(答案不唯一)
10.[答案] 5
∵四边形ABCD与四边形A′B′C′D′位似,其位似中心为点O,OC=6,CC′=4,
∴==,
∴=.
又∵AB=3,∴A′B′=5.
11.[答案]
易得△BCD∽△BAC,从而BC∶BA=BD∶BC,代入求得BD=.
12.[答案] (,2)
∵将△AOB以点O为位似中心,为位似比作位似变换,得到△A1OB1,A(2,3),∴点A1的坐标是(×2,×3),即A1(,2).故答案为(,2).
13.[答案] 10
14.[答案] 5
∵在Rt△ABC中,AC=1,BC=2,
∴AB=,AC∶BC=1∶2,
∴与Rt△ABC相似的格点三角形的两直角边的比值为1∶2.
若该三角形最短边长为4,则另一直角边长为8,但在6×6网格图形中,最长线段为6 ,但此时画出的直角三角形为等腰直角三角形,从而画不出端点都在格点且长为8的线段,故最短直角边长应小于4,在图中尝试,可画出DE=,EF=2 ,DF=5 的三角形,
∵===,
∴△ABC∽△DFE,
∴∠DEF=∠C=90°,
∴此时△DEF的面积为×2 ÷2=10,△DEF为所求面积最大的三角形,其斜边长为5 .
15.证明:∵AD,BE是钝角三角形ABC的高,
∴∠ADC=∠BEC=90°.
又∵∠DCA=∠BCE,
∴△DAC∽△EBC,
∴=.
16.解:(1)(2)画图如下图所示,B2(10,8).
17.解:过点C作CH⊥AB于点H,交EF于点P,则CH=AD=25 m,CP=40 cm=0.4 m,EF=20 cm=0.2 m.
由题意,得EF∥AB,
∴△CEF∽△CBA,
∴=,即=,
解得BA=12.5(m).
答:旗杆BA的高度为12.5 m.
18.解:(1)四边形GECF是菱形.理由:
∵EG=EC,DE⊥AC,
∴GO=CO.
∵GF∥AD,AD∥BC,
∴GF∥BC,
∴∠FGO=∠ECO,∠GFO=∠CEO,
∴△GFO≌△CEO(AAS),
∴GF=EC.
又∵GF∥EC,
∴四边形GECF是平行四边形.
又∵EG=EC,
∴四边形GECF是菱形.
(2)证明:∵∠DHC=∠DAH+∠ADH=∠DHF+∠FHC,∠DHF=∠HAD,
∴∠ADH=∠FHC.
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAH=∠ACB.
∵四边形GECF是菱形,
∴CE=CF,∠HCF=∠ACB,
∴∠HCF=∠DAH,
∴△ADH∽△CHF,
则=.
又∵CF=EC,∴AH·CH=EC·AD.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
