3.2.2 用移项的方法解一元一次方程 课件(共23张PPT)
文档属性
| 名称 | 3.2.2 用移项的方法解一元一次方程 课件(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-24 00:00:00 | ||
图片预览







文档简介
(共23张PPT)
3.2.2 用移项的方法解一元一次方程
人教版七年级上册
教学目标
教学目标: 1. 掌握含有括号的方程中“去括号”的方法步骤;
2. 进一步学习列方程解应用题,培养学生分析问题的能力.
教学重点:建立列方程解决实际问题的思想方法,学会移项,会解
“ax+b=cx+d”类型的一元一次方程.
教学难点: 分析实际问题中的已经量和未知量,找出相等关系,列出方程,
使使学生逐步建立列方程解决实际问题的思想方法.
新知导入
情境引入
前面,我们学习了利用合并同类项解一元一次方程,所见到的方程基本上都是含未知数的项在等号的一边(左边),常数项在等号的另一边(右边),如果等号两边都有含未知数的项和常数项,那么这样的方程该怎样求解呢?这节课我们继续学习解一元一次方程的方法——移项.
新知讲解
合作学习
1、设未知数:设这个班有x名学生.
2、找相等关系:这批书的总数是一个定值,表示它的两个等式相等.
3、列方程:
每人分3本,共分出3x本,加上剩余的20本,这批书共 本.
每人分4本,需要 本,减去缺的25本,这批书共 本.
3x+20
4x
4x-25
把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.这个班有多少学生?
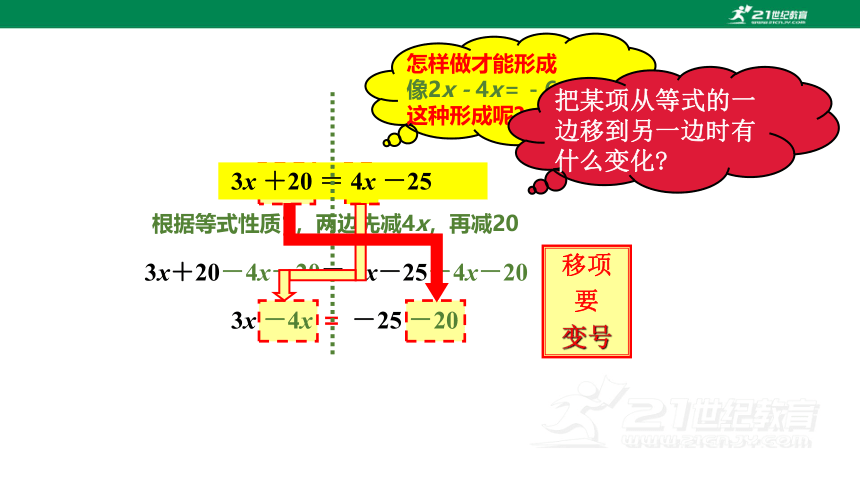
3x+20 = 4x-25
3x +20 = 4x -25
怎样做才能形成
像2x-4x=-6+7
这种形成呢
根据等式性质1,两边先减4x,再减20
3x+20-4x-20= 4x-25-4x-20
3x -4x = -25 -20
把某项从等式的一边移到另一边时有什么变化
移项
要
变号
3x+20=4x-25
3x+20-4x=4x-25-4x
3x+20-4x=-25
3x+20-4x-20=-25-20
3x-4x=-25-20
(合并同类项)
(利用等式性质1)
(利用等式性质1)
(合并同类项)
思考:怎样解这个方程?它与上节课遇到的方程有何不同?
3x+20=4x-25
3x-4x=-25-20
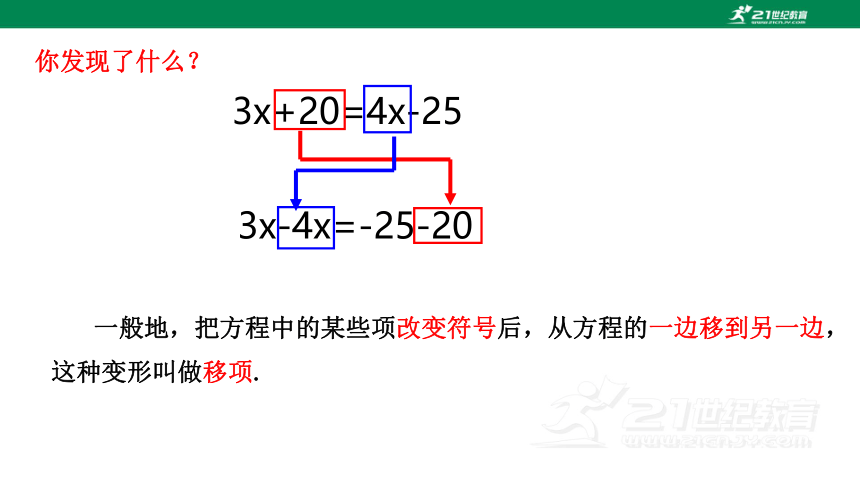
你发现了什么?
一般地,把方程中的某些项改变符号后,从方程的一边移到另一边,这种变形叫做移项.
3x+20=4x-25
3x-4x=-25-20
-x=-45
x=45
移项
合并同类项
系数化为1
下面的框图表示了解这个方程的具体过程:
左边仅含
未知数项
右边仅含
常数项
提炼概念
通过移项,使等号左边仅含未知数的项,等号右边仅含常数的项,
目的是便于合并同类项,使方程更接近x=a的形式.
思考2:“移项”起了什么作用?
思考1:以上解方程“移项”的依据是什么?
移项的依据是等式的性质1.
典例精讲
系数化为1,得 x=5.
解:(1)移项,得 3x+2x=32-7.
合并同类项,得 5x=25
例1 解下列方程(1)3x+7=32-2x;
系数化为1,得 x=-8
(2) 移项,得
合并同类项,得
备注:移项时应注意改变项的符号; 步骤为“一移二并三化”
例2 某制药厂制造一批药品,如用旧工艺,则废水排量要比环保限制的最大量还多200 t;如用新工艺,则废水排量比环保限制的最大量少100 t. 新旧工艺的废水排量之比为2:5,两种工艺的废水排量各是多少?
思考: (1)你准备设哪个未知数?
(2)你能在问题中把表示等量关系的语句
找出来,并用等式进行表示吗?
解:设新、旧工艺的废水排量分别为2x t和5x t.根据废水排量与环保限制最大量之间的关系,得
5x-200=2x+100
移项,得 5x-2x=100+200
合并同类项,得3x=300
系数化为1,得 x=100
所以 2x=200,5x=500.
答:新旧工艺产生的废水数量分别为200 t和500 t.
归纳概念
解决比例问题,一般设每份为未知数,用含未知数的式子表示相关的量,再根据等量关系列出方程.
课堂练习
1. 解方程时,移项法则的依据是( )
A.加法交换律 B.加法结合律
C.等式的性质1 D.等式的性质2
C
2.下列变形中,属于移项的是( )
A.由3x=-1,得 B .由 ,得x=4
C.由3x+5=0,得3x=-5 D.由-3x+3=0,得3-3x=0
C
3.方程4x-2=3-x有下列解答过程:①合并同类项,得5x=5;②移项,
得4x+x=3+2;③系数化为1,得x=1.正确的解题顺序是( )
A.①②③ B .③②①
C.②①③ D.③①②
C
4.在某地区2014年“地球停电一小时”活动的烛光晚餐中,设有x排座
位,每排坐30人,则有8人无座位;每排坐31人,则空26个座位,则
下列方程正确的是( )
A.30x-8=31x+26
B.30x+8=31x+26
C.30x-8=31x-26
D.30x+8=31x-26
D
5.解下列方程
解:
合并同类项,得
系数化为1,得
合并同类项,得
系数化为1,得
(1)移项,得
6x-4x=-5+7
2x=2
x=1
(2)移项,得
x=-24
6. 某同学在解关于x的方程3a=2x+15时,在移项过程中2x没有改变符号,得到的方程的解为x=3.求a的值及原方程的解.
解:根据题意知,x=3是关于x的方程2x=15-3a的解,
所以2×3=15-3a,解得a=3.
把a=3代入原方程,得3×3=2x+15.
所以2x=-6,即x=-3.
所以,a的值是3,原方程的解是x=-3.
7. 小新出生时父亲28岁,现在父亲的年龄比小新年龄的3倍小2岁. 求小新现在的年龄.
解:设小新现在的年龄为x岁.
根据题意,得 3x – 2 = x + 28.
移项,得 2x = 30.
系数化为1,得 x = 15.
答:小新现在的年龄是15岁.
课堂总结
用移项法解一元一次方程的一般步骤:
移项→合并同类项→系数化为1.
移项的原则:
未知项左边来报到,常数项右边凑热闹.
移项的方法:
把方程中的某些项改变符号后,从方程的一边移到另一边,即移项要变号.
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
3.2.2 用移项的方法解一元一次方程
人教版七年级上册
教学目标
教学目标: 1. 掌握含有括号的方程中“去括号”的方法步骤;
2. 进一步学习列方程解应用题,培养学生分析问题的能力.
教学重点:建立列方程解决实际问题的思想方法,学会移项,会解
“ax+b=cx+d”类型的一元一次方程.
教学难点: 分析实际问题中的已经量和未知量,找出相等关系,列出方程,
使使学生逐步建立列方程解决实际问题的思想方法.
新知导入
情境引入
前面,我们学习了利用合并同类项解一元一次方程,所见到的方程基本上都是含未知数的项在等号的一边(左边),常数项在等号的另一边(右边),如果等号两边都有含未知数的项和常数项,那么这样的方程该怎样求解呢?这节课我们继续学习解一元一次方程的方法——移项.
新知讲解
合作学习
1、设未知数:设这个班有x名学生.
2、找相等关系:这批书的总数是一个定值,表示它的两个等式相等.
3、列方程:
每人分3本,共分出3x本,加上剩余的20本,这批书共 本.
每人分4本,需要 本,减去缺的25本,这批书共 本.
3x+20
4x
4x-25
把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.这个班有多少学生?
3x+20 = 4x-25
3x +20 = 4x -25
怎样做才能形成
像2x-4x=-6+7
这种形成呢
根据等式性质1,两边先减4x,再减20
3x+20-4x-20= 4x-25-4x-20
3x -4x = -25 -20
把某项从等式的一边移到另一边时有什么变化
移项
要
变号
3x+20=4x-25
3x+20-4x=4x-25-4x
3x+20-4x=-25
3x+20-4x-20=-25-20
3x-4x=-25-20
(合并同类项)
(利用等式性质1)
(利用等式性质1)
(合并同类项)
思考:怎样解这个方程?它与上节课遇到的方程有何不同?
3x+20=4x-25
3x-4x=-25-20
你发现了什么?
一般地,把方程中的某些项改变符号后,从方程的一边移到另一边,这种变形叫做移项.
3x+20=4x-25
3x-4x=-25-20
-x=-45
x=45
移项
合并同类项
系数化为1
下面的框图表示了解这个方程的具体过程:
左边仅含
未知数项
右边仅含
常数项
提炼概念
通过移项,使等号左边仅含未知数的项,等号右边仅含常数的项,
目的是便于合并同类项,使方程更接近x=a的形式.
思考2:“移项”起了什么作用?
思考1:以上解方程“移项”的依据是什么?
移项的依据是等式的性质1.
典例精讲
系数化为1,得 x=5.
解:(1)移项,得 3x+2x=32-7.
合并同类项,得 5x=25
例1 解下列方程(1)3x+7=32-2x;
系数化为1,得 x=-8
(2) 移项,得
合并同类项,得
备注:移项时应注意改变项的符号; 步骤为“一移二并三化”
例2 某制药厂制造一批药品,如用旧工艺,则废水排量要比环保限制的最大量还多200 t;如用新工艺,则废水排量比环保限制的最大量少100 t. 新旧工艺的废水排量之比为2:5,两种工艺的废水排量各是多少?
思考: (1)你准备设哪个未知数?
(2)你能在问题中把表示等量关系的语句
找出来,并用等式进行表示吗?
解:设新、旧工艺的废水排量分别为2x t和5x t.根据废水排量与环保限制最大量之间的关系,得
5x-200=2x+100
移项,得 5x-2x=100+200
合并同类项,得3x=300
系数化为1,得 x=100
所以 2x=200,5x=500.
答:新旧工艺产生的废水数量分别为200 t和500 t.
归纳概念
解决比例问题,一般设每份为未知数,用含未知数的式子表示相关的量,再根据等量关系列出方程.
课堂练习
1. 解方程时,移项法则的依据是( )
A.加法交换律 B.加法结合律
C.等式的性质1 D.等式的性质2
C
2.下列变形中,属于移项的是( )
A.由3x=-1,得 B .由 ,得x=4
C.由3x+5=0,得3x=-5 D.由-3x+3=0,得3-3x=0
C
3.方程4x-2=3-x有下列解答过程:①合并同类项,得5x=5;②移项,
得4x+x=3+2;③系数化为1,得x=1.正确的解题顺序是( )
A.①②③ B .③②①
C.②①③ D.③①②
C
4.在某地区2014年“地球停电一小时”活动的烛光晚餐中,设有x排座
位,每排坐30人,则有8人无座位;每排坐31人,则空26个座位,则
下列方程正确的是( )
A.30x-8=31x+26
B.30x+8=31x+26
C.30x-8=31x-26
D.30x+8=31x-26
D
5.解下列方程
解:
合并同类项,得
系数化为1,得
合并同类项,得
系数化为1,得
(1)移项,得
6x-4x=-5+7
2x=2
x=1
(2)移项,得
x=-24
6. 某同学在解关于x的方程3a=2x+15时,在移项过程中2x没有改变符号,得到的方程的解为x=3.求a的值及原方程的解.
解:根据题意知,x=3是关于x的方程2x=15-3a的解,
所以2×3=15-3a,解得a=3.
把a=3代入原方程,得3×3=2x+15.
所以2x=-6,即x=-3.
所以,a的值是3,原方程的解是x=-3.
7. 小新出生时父亲28岁,现在父亲的年龄比小新年龄的3倍小2岁. 求小新现在的年龄.
解:设小新现在的年龄为x岁.
根据题意,得 3x – 2 = x + 28.
移项,得 2x = 30.
系数化为1,得 x = 15.
答:小新现在的年龄是15岁.
课堂总结
用移项法解一元一次方程的一般步骤:
移项→合并同类项→系数化为1.
移项的原则:
未知项左边来报到,常数项右边凑热闹.
移项的方法:
把方程中的某些项改变符号后,从方程的一边移到另一边,即移项要变号.
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
