2022-2023学年苏科版数学七年级上册3.2代数式 同步练习 (word解析版)
文档属性
| 名称 | 2022-2023学年苏科版数学七年级上册3.2代数式 同步练习 (word解析版) |

|
|
| 格式 | docx | ||
| 文件大小 | 188.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-26 20:22:20 | ||
图片预览



文档简介
3.2代数式(同步练习)
一.选择题(共10小题)
1.单项式﹣3πxy2z3的系数和次数分别是( )
A.﹣π,5 B.﹣1,6 C.﹣3π,6 D.﹣3,7
2.下列语句中错误的是( )
A.数字0也是单项式
B.单项式﹣a的系数与次数都是1
C.xy是二次单项式
D.的系数是
3.若关于x,y的多项式化简后不含二次项,则m=( )
A. B. C. D.0
4.若多项式3x|m|+(m﹣2)x+1是关于x的二次三项式,则m的值( )
A.2或﹣2 B.2 C.﹣2 D.﹣4
5.下列说法中,正确的是( )
A.单项式xy2的系数是x
B.单项式﹣5x2的次数为﹣5
C.多项式x2+2x+18是二次三项式
D.多项式x2+y2﹣1的常数项是1
6.在式子,2πx2y,,y2﹣5,π+6,中,多项式的个数是( )
A.1 B.2 C.3 D.4
7.下列代数式:(1)mn,(2)m,(3),(4),(5)2m+1,(6),(7),(8)x2+2x,(9)y3﹣5y中,整式有( )
A.3个 B.4个 C.6个 D.7个
8.在代数式a+b,x2,,﹣m,0,,中,单项式的个数是( )
A.6 B.5 C.4 D.3
9.某九年级学生复习了整式有关概念后,他用一个圆代表所有代数式,画了下列图形来表示整式,多项式,单项式的关系,正确的是( )
10.下面每个表格中的四个数都是按相同规律填写的:
根据此规律确定x的值为( )
A.135 B.170 C.209 D.252
二.填空题(共10小题)
11.单项式的系数是 .
12.如果一个单项式的系数和次数分别为m、n,那么2mn= .
13.把多项式2m3﹣m2n2+3﹣5m按字母m的升幂排列是 .
14.多项式3x2y﹣7x4y2﹣xy3+28是 次 项式,最高次项的系数是 .
15.多项式x+7是关于x的二次三项式,则m= .
16.多项式x|m|﹣(m﹣3)x+6是关于x的三次三项式,则m的值是 .
17.已知关于x的多项式(m﹣2)x2﹣mx+3中的x的一次项系数为﹣2,则这个多项式是 次 项式.
18.若单项式﹣x3yn+5的系数是m,次数是9,则m+n的值为 .
19.若代数式6amb4是六次单项式.则m= .
20.若多项式(k﹣1)x2+3x|k+2|+2为三次三项式,则k的值为 .
三.解答题(共10小题)
21.下列代数式中的哪些是单项式,哪些是多项式,哪些是整式?
,4xy,,,x2+x,0,,m,﹣2.01×105
整式集合:{ …}
单项式集合:{ …}
多项式集合:{ …}.
22.已知x2y|a|+(b+2)是关于x、y的五次单项式,求a2﹣3ab的值.
23.观察下列一串单项式的特点:xy,﹣2x2y,4x3y,﹣8x4y,16x5y,…
(1)按此规律写出第9个单项式;
(2)试猜想第n个单项式为多少?它的系数和次数分别是多少?
24.观察下面有规律的三行单项式:
x,2x2,4x3,8x4,16x5,32x6,…①
﹣2x,4x2,﹣8x3,16x4,﹣32x5,64x6,…②
2x2,﹣3x3,5x4,﹣9x5,17x6,﹣33x7,…③
(1)根据你发现的规律,第一行第8个单项式为 ;
(2)第二行第n个单项式为 ;
(3)第三行第8个单项式为 ;第n个单项式为 .
25.已知有理数a和b满足多项式A.A=(a﹣1)x5+x|b+2|﹣2x2+bx+b是关于x的二次三项式.当x<﹣7时,化简:|x﹣a|+|x﹣b|
26.对于多项式(n﹣1)xm+2﹣3x2+2x(m,n为常数,且m是大于﹣2的整数).
(1)若n=2,且该多项式是关于x的三次三项式,求m的值;
(2)若该多项式化简后是关于x的二次单项式,求m,n的值;
(3)若该多项式是关于x的二次二项式,则m,n要满足什么条件?
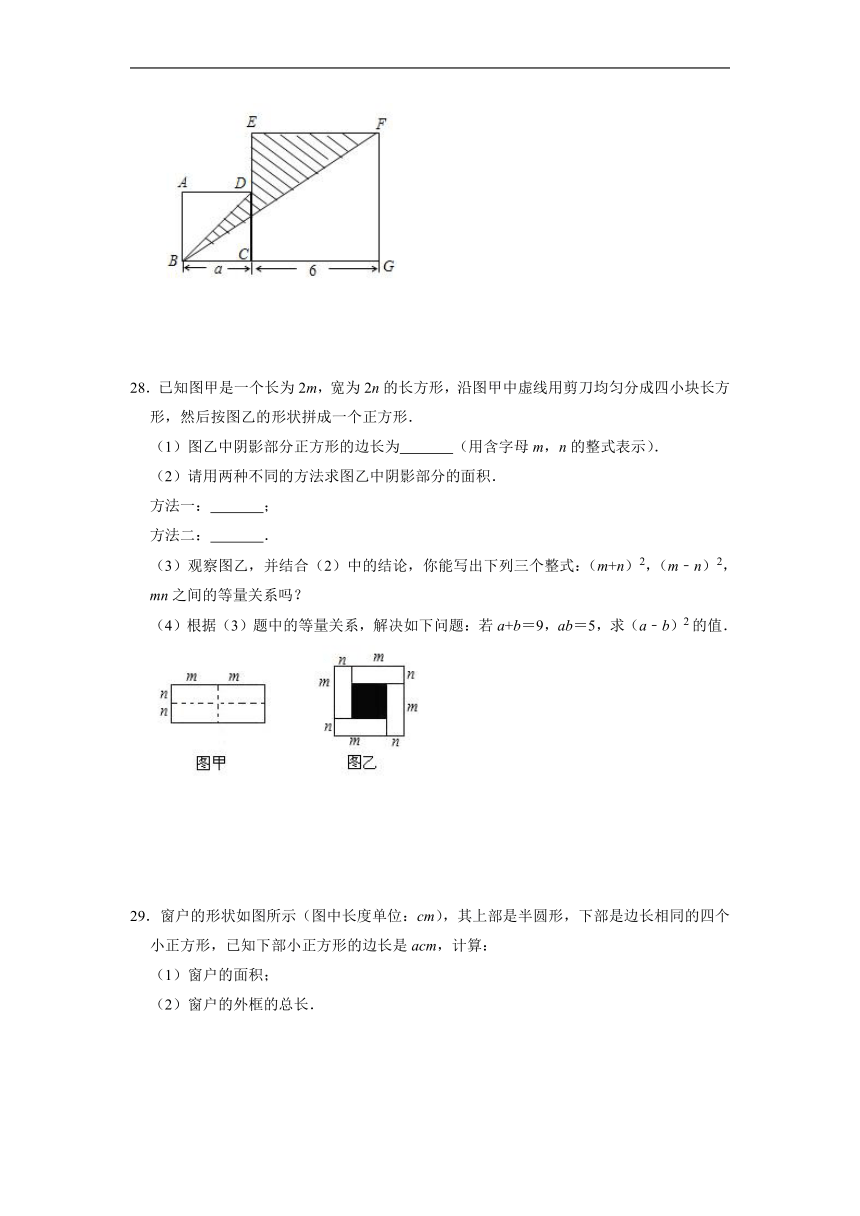
27.如图,四边形ABCD和ECGF都是正方形.
(1)写出表示阴影部分面积的代数式;(结果要求化简)
(2)当a=4时,求阴影部分的面积.
28.已知图甲是一个长为2m,宽为2n的长方形,沿图甲中虚线用剪刀均匀分成四小块长方形,然后按图乙的形状拼成一个正方形.
(1)图乙中阴影部分正方形的边长为 (用含字母m,n的整式表示).
(2)请用两种不同的方法求图乙中阴影部分的面积.
方法一: ;
方法二: .
(3)观察图乙,并结合(2)中的结论,你能写出下列三个整式:(m+n)2,(m﹣n)2,mn之间的等量关系吗?
(4)根据(3)题中的等量关系,解决如下问题:若a+b=9,ab=5,求(a﹣b)2的值.
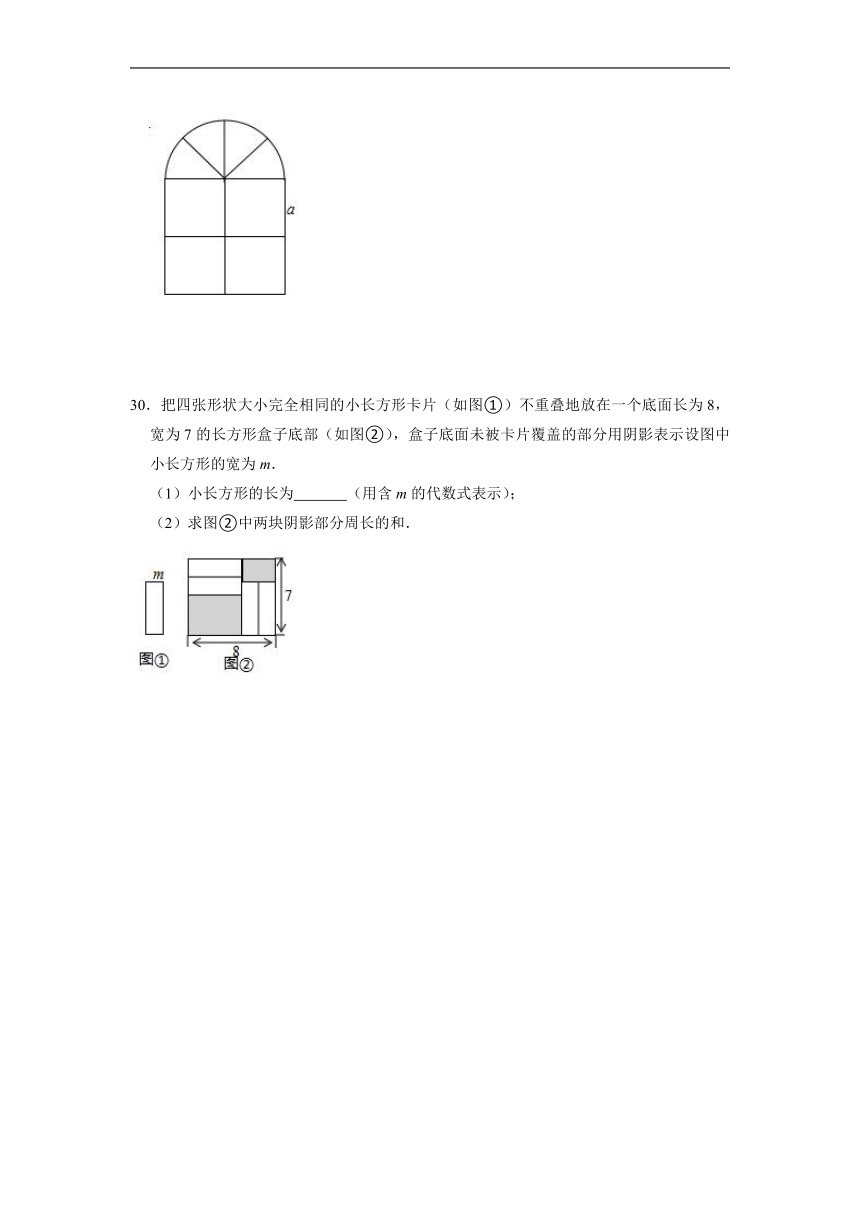
29.窗户的形状如图所示(图中长度单位:cm),其上部是半圆形,下部是边长相同的四个小正方形,已知下部小正方形的边长是acm,计算:
(1)窗户的面积;
(2)窗户的外框的总长.
30.把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面长为8,宽为7的长方形盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示设图中小长方形的宽为m.
(1)小长方形的长为 (用含m的代数式表示);
(2)求图②中两块阴影部分周长的和.
3.2代数式(同步练习解析)
一.选择题(共10小题)
1.单项式﹣3πxy2z3的系数和次数分别是( )
A.﹣π,5 B.﹣1,6 C.﹣3π,6 D.﹣3,7
【解答】解:根据单项式系数、次数的定义,单项式﹣3πxy2z3的系数和次数分别是﹣3π,6.
故选:C.
2.下列语句中错误的是( )
A.数字0也是单项式
B.单项式﹣a的系数与次数都是1
C.xy是二次单项式
D.的系数是
【解答】解:单独的一个数字也是单项式,故A正确;
单项式﹣a的系数应是﹣1,次数是1,故B错误;
xy的次数是2,符合单项式的定义,故C正确;
的系数是,故D正确.
故选:B.
3.若关于x,y的多项式化简后不含二次项,则m=( )
A. B. C. D.0
【解答】解:∵原式x2y+(6﹣7m)xyy3,
若不含二次项,即6﹣7m=0,
解得m.
故选:B.
4.若多项式3x|m|+(m﹣2)x+1是关于x的二次三项式,则m的值( )
A.2或﹣2 B.2 C.﹣2 D.﹣4
【解答】解:因为多项式3x|m|+(m﹣2)x+1是关于x的二次三项式,
所以|m|=2,且m﹣2≠0,
解得m=±2,且m≠2,
则m的值为﹣2.
故选:C.
5.下列说法中,正确的是( )
A.单项式xy2的系数是x
B.单项式﹣5x2的次数为﹣5
C.多项式x2+2x+18是二次三项式
D.多项式x2+y2﹣1的常数项是1
【解答】解:A、单项式xy2的系数是,原说法错误,故此选项不符合题意;
B、单项式﹣5x2的次数为2,原说法错误,故此选项不符合题意;
C、多项式x2+2x+18是二次三项式,原说法正确,故此选项符合题意;
D、多项式x2+y2﹣1的常数项是﹣1,原说法错误,故此选项不符合题意,
故选:C.
6.在式子,2πx2y,,y2﹣5,π+6,中,多项式的个数是( )
A.1 B.2 C.3 D.4
【解答】解:在式子,2πx2y,,y2﹣5,π+6,中,
多项式有:,y2﹣5,共2个.
故选:B.
7.下列代数式:(1)mn,(2)m,(3),(4),(5)2m+1,(6),(7),(8)x2+2x,(9)y3﹣5y中,整式有( )
A.3个 B.4个 C.6个 D.7个
【解答】解:根据整式的概念可知,整式有:
(1)mn;(2)m;(3);(5)2m+1;(6);(8)x2+2x.共6个.
故选:C.
8.在代数式a+b,x2,,﹣m,0,,中,单项式的个数是( )
A.6 B.5 C.4 D.3
【解答】解:x2,﹣m,0是单项式,
故选:D.
9.某九年级学生复习了整式有关概念后,他用一个圆代表所有代数式,画了下列图形来表示整式,多项式,单项式的关系,正确的是( )
【解答】解:代数式包括整式和分式,整式包括多项式和单项式,故正确的是选项D,
故选:D.
10.下面每个表格中的四个数都是按相同规律填写的:
根据此规律确定x的值为( )
A.135 B.170 C.209 D.252
【解答】解:∵a+(a+2)=20,
∴a=9,
∵b=a+1,
∴b=a+1=9+1=10,
∴x=20b+a
=20×10+9
=200+9
=209
故选:C.
二.填空题(共10小题)
11.单项式的系数是 .
【解答】解:单项式的系数是,
故答案为:.
12.如果一个单项式的系数和次数分别为m、n,那么2mn= ﹣2 .
【解答】解:由题意可知:m,n=3,
∴2mn=2×()×3=﹣2.
故答案为:﹣2.
13.把多项式2m3﹣m2n2+3﹣5m按字母m的升幂排列是 +3﹣5m﹣m2n2+2m3 .
【解答】解:把多项式2m3﹣m2n2+3﹣5m按字母m的升幂排列是+3﹣5m﹣m2n2+2m3.
故答案为:+3﹣5m﹣m2n2+2m3.
14.多项式3x2y﹣7x4y2﹣xy3+28是 六 次 四 项式,最高次项的系数是 ﹣7 .
【解答】解:多项式3x2y﹣7x4y2﹣xy3+28是六次四项式,最高次项的系数是﹣7.
故答案为六、四、﹣7
15.多项式x+7是关于x的二次三项式,则m= 2 .
【解答】解:∵多项式是关于x的二次三项式,
∴|m|=2,
∴m=±2,
但﹣(m+2)≠0,
即m≠﹣2,
综上所述,m=2,故填空答案:2.
16.多项式x|m|﹣(m﹣3)x+6是关于x的三次三项式,则m的值是 ﹣3 .
【解答】解:∵多项式是关于x的三次三项式,
∴|m|=3,
∴m=±3,
但m﹣3≠0,
即m≠3,
综上所述m=﹣3.
故答案为:﹣3.
17.已知关于x的多项式(m﹣2)x2﹣mx+3中的x的一次项系数为﹣2,则这个多项式是 一 次 二 项式.
【解答】解:∵多项式(m﹣2)x2﹣mx+3中的x的一次项系数为﹣2,∴﹣m=﹣2,m=2,
把m=2代入多项式(m﹣2)x2﹣mx+3中,m﹣2=0,∴二次项系数为0,多项式为一次二项式.
18.若单项式﹣x3yn+5的系数是m,次数是9,则m+n的值为 0 .
【解答】解:根据题意得:m=﹣1,3+n+5=9,
解得:m=﹣1,n=1,
则m+n=﹣1+1=0.
故答案为:0.
19.若代数式6amb4是六次单项式.则m= 2 .
【解答】解:若代数式6amb4是六次单项式,则m=2.
故答案为:2.
20.若多项式(k﹣1)x2+3x|k+2|+2为三次三项式,则k的值为 ﹣5 .
【解答】解:∵多项式(k﹣1)x2+3x|k+2|+2是关于x的三次三项式,
∴|k+2|=3,k﹣1≠0,
解得:k=﹣5.
故答案为:﹣5.
三.解答题(共10小题)
21.下列代数式中的哪些是单项式,哪些是多项式,哪些是整式?
,4xy,,,x2+x,0,,m,﹣2.01×105
整式集合:{ ,4xy,,0,m,﹣2.01×105 …}
单项式集合:{ 4xy,,0,m,﹣2.01×105 …}
多项式集合:{ …}.
【解答】解:整式集合:{,4xy,,0,m,﹣2.01×105 …};
单项式集合:{ 4xy,,0,m,﹣2.01×105 …};
多项式集合:{ …}.
故答案为:{,4xy,,0,m,﹣2.01×105 …};{ 4xy,,0,m,﹣2.01×105 …};{ …}.
22.已知x2y|a|+(b+2)是关于x、y的五次单项式,求a2﹣3ab的值.
【解答】解:∵x2y|a|+(b+2)是关于x,y的五次单项式,
∴,
解得:,
则当a=﹣3,b=﹣2时,a2﹣3ab=9﹣18=﹣9;
当a=3,b=﹣2时,a2﹣3ab=9+18=27.
23.观察下列一串单项式的特点:xy,﹣2x2y,4x3y,﹣8x4y,16x5y,…
(1)按此规律写出第9个单项式;
(2)试猜想第n个单项式为多少?它的系数和次数分别是多少?
【解答】解:(1)∵当n=1时,xy,
当n=2时,﹣2x2y,
当n=3时,4x3y,
当n=4时,﹣8x4y,
当n=5时,16x5y,
∴第9个单项式是29﹣1x9y,即256x9y.
(2)∴n为偶数时,单项式为负数.x的指数为n时,2的指数为n﹣1,
∴当n为奇数时的单项式为2n﹣1xny,
该单项式为(﹣1)n+12n﹣1xny
它的系数是(﹣1)n+12n﹣1,次数是n+1.
24.观察下面有规律的三行单项式:
x,2x2,4x3,8x4,16x5,32x6,…①
﹣2x,4x2,﹣8x3,16x4,﹣32x5,64x6,…②
2x2,﹣3x3,5x4,﹣9x5,17x6,﹣33x7,…③
(1)根据你发现的规律,第一行第8个单项式为 128x8 ;
(2)第二行第n个单项式为 (﹣2)nxn ;
(3)第三行第8个单项式为 ﹣129x9 ;第n个单项式为 (﹣1)n+1(1+2n﹣1)xn+1 .
【解答】解:(1)因为第一行的每个单项式,数字因数后面都是前面的2倍,字母次数与这个单项式是第几个有关,根据这个规律可得第一行第8个单项式为 128x8;
(2)因为第二行的每个单项式,数字因数后面都是前面的(﹣2)倍,字母次数与这个单项式是第几个有关,根据这个规律可得第n个单项式为 (﹣2)nxn;
(3)通过观察第三行的这组单项式,这组单项式符合 (﹣1)n+1(1+2n﹣1)xn+1,第8个单项式是﹣129x9;第n个单项式为 (﹣1)n+1(1+2n﹣1)xn+1.
故答案为:(1)128x8,(2)(﹣2x)n,(3)﹣129x9 ,(﹣1)n+1(1+2n﹣1)xn+1
25.已知有理数a和b满足多项式A.A=(a﹣1)x5+x|b+2|﹣2x2+bx+b是关于x的二次三项式.当x<﹣7时,化简:|x﹣a|+|x﹣b|
【解答】解:∵有理数a和b满足多项式A.A=(a﹣1)x5+x|b+2|﹣2x2+bx+b是关于x的二次三项式,
∴a﹣1=0,解得a=1.
当|b+2|=2时,解得b=0,此时A不是二次三项式;或b=﹣4,此时A是关于x的二次三项式,
当|b+2|=1时,解得b=﹣1或b=﹣3,
当|b+2|=0时,解得b=﹣2,
当5次项和|b+2|是同类项,并且系数互为相反数时,a=0,b=3或﹣7,
∴当a=1,b=﹣1,x<﹣7时,不是二次三项式;
当a=1,b=﹣2,x<﹣7时,|x﹣a|+|x﹣b|=|x﹣1|+|x+2|=1﹣x﹣x﹣2=﹣2x﹣1
当a=1,b=﹣3,x<﹣7时,|x﹣a|+|x﹣b|=|x﹣1|+|x+3|=1﹣x﹣x﹣3=﹣2x﹣2;
当a=1,b=﹣4,x<﹣7时,|x﹣a|+|x﹣b|=|x﹣1|+|x+4|=1﹣x﹣x﹣4=﹣2x﹣3;
当a=0,b=3,x<﹣7时,|x﹣a|+|x﹣b|=|x|+|x﹣3|=﹣x﹣x+3=﹣2x+3;
当a=0,b=﹣7,x<﹣7时,|x﹣a|+|x﹣b|=|x|+|x+7|=﹣x﹣x﹣7=﹣2x﹣7.
26.对于多项式(n﹣1)xm+2﹣3x2+2x(m,n为常数,且m是大于﹣2的整数).
(1)若n=2,且该多项式是关于x的三次三项式,求m的值;
(2)若该多项式化简后是关于x的二次单项式,求m,n的值;
(3)若该多项式是关于x的二次二项式,则m,n要满足什么条件?
【解答】解:(1)当n=2时,且该多项式是关于x的三次三项式,
故原式=xm+2﹣3x2+2x,m+2=3,解得:m=1;
(2)若该多项式是关于x的二次单项式,
则m+2=1,n﹣1=﹣2,
解得:m=﹣1,n=﹣1;
(3)若该多项式是关于x的二次二项式,
①n﹣1=0,m是大于﹣2的整数.
则m,n要满足的条件是:n=1,m是大于﹣2的整数;
②当m=﹣1时,n≠﹣1,
③m=0时,n≠4.
27.如图,四边形ABCD和ECGF都是正方形.
(1)写出表示阴影部分面积的代数式;(结果要求化简)
(2)当a=4时,求阴影部分的面积.
【解答】解:(1)S=a2+62a2(a+6)6=a2+62a2a×662a2﹣3a+18.
(2)当a=4cm,S42﹣3×4+18=14.
28.已知图甲是一个长为2m,宽为2n的长方形,沿图甲中虚线用剪刀均匀分成四小块长方形,然后按图乙的形状拼成一个正方形.
(1)图乙中阴影部分正方形的边长为 m﹣n (用含字母m,n的整式表示).
(2)请用两种不同的方法求图乙中阴影部分的面积.
方法一: (m+n)2﹣4mn ;
方法二: (m﹣n)2 .
(3)观察图乙,并结合(2)中的结论,你能写出下列三个整式:(m+n)2,(m﹣n)2,mn之间的等量关系吗?
(4)根据(3)题中的等量关系,解决如下问题:若a+b=9,ab=5,求(a﹣b)2的值.
【解答】解:(1)图乙中阴影部分正方形的边长为m﹣n;
(2)方法一:(m+n)2﹣4mn;
方法二:(m﹣n)2;
(3)(m+n)2﹣4mn=(m﹣n)2;
(4)(a﹣b)2=(a+b)2﹣4ab,
∵a+b=9,ab=5,
∴(a﹣b)2=81﹣20=61.
故答案为:m﹣n;(m+n)2﹣4mn;(m﹣n)2.
29.窗户的形状如图所示(图中长度单位:cm),其上部是半圆形,下部是边长相同的四个小正方形,已知下部小正方形的边长是acm,计算:
(1)窗户的面积;
(2)窗户的外框的总长.
【解答】解:(1)窗户的面积是:
4a2+πa2÷2
=4a2+0.5πa2
=(4+0.5π)a2(cm2)
(2)窗户的外框的总长是:
2a×3+πa
=6a+πa
=(6+π)a(cm)
30.把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面长为8,宽为7的长方形盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示设图中小长方形的宽为m.
(1)小长方形的长为 8﹣2m (用含m的代数式表示);
(2)求图②中两块阴影部分周长的和.
【解答】解:(1)小长方形的长为8﹣2m.
故答案为:8﹣2m;
(2)设小长方形卡片的长为n,
则右上小长方形周长为2×(8﹣n+7﹣n)=30﹣4n,
左下小长方形周长为2×(n+7﹣2m)=2n+14﹣4m,
∴两块阴影部分周长和=30﹣4n+2n+14﹣4m=44﹣2(n+2m)
∵8=n+2m,
∴两块阴影部分周长和=44﹣16=28.
一.选择题(共10小题)
1.单项式﹣3πxy2z3的系数和次数分别是( )
A.﹣π,5 B.﹣1,6 C.﹣3π,6 D.﹣3,7
2.下列语句中错误的是( )
A.数字0也是单项式
B.单项式﹣a的系数与次数都是1
C.xy是二次单项式
D.的系数是
3.若关于x,y的多项式化简后不含二次项,则m=( )
A. B. C. D.0
4.若多项式3x|m|+(m﹣2)x+1是关于x的二次三项式,则m的值( )
A.2或﹣2 B.2 C.﹣2 D.﹣4
5.下列说法中,正确的是( )
A.单项式xy2的系数是x
B.单项式﹣5x2的次数为﹣5
C.多项式x2+2x+18是二次三项式
D.多项式x2+y2﹣1的常数项是1
6.在式子,2πx2y,,y2﹣5,π+6,中,多项式的个数是( )
A.1 B.2 C.3 D.4
7.下列代数式:(1)mn,(2)m,(3),(4),(5)2m+1,(6),(7),(8)x2+2x,(9)y3﹣5y中,整式有( )
A.3个 B.4个 C.6个 D.7个
8.在代数式a+b,x2,,﹣m,0,,中,单项式的个数是( )
A.6 B.5 C.4 D.3
9.某九年级学生复习了整式有关概念后,他用一个圆代表所有代数式,画了下列图形来表示整式,多项式,单项式的关系,正确的是( )
10.下面每个表格中的四个数都是按相同规律填写的:
根据此规律确定x的值为( )
A.135 B.170 C.209 D.252
二.填空题(共10小题)
11.单项式的系数是 .
12.如果一个单项式的系数和次数分别为m、n,那么2mn= .
13.把多项式2m3﹣m2n2+3﹣5m按字母m的升幂排列是 .
14.多项式3x2y﹣7x4y2﹣xy3+28是 次 项式,最高次项的系数是 .
15.多项式x+7是关于x的二次三项式,则m= .
16.多项式x|m|﹣(m﹣3)x+6是关于x的三次三项式,则m的值是 .
17.已知关于x的多项式(m﹣2)x2﹣mx+3中的x的一次项系数为﹣2,则这个多项式是 次 项式.
18.若单项式﹣x3yn+5的系数是m,次数是9,则m+n的值为 .
19.若代数式6amb4是六次单项式.则m= .
20.若多项式(k﹣1)x2+3x|k+2|+2为三次三项式,则k的值为 .
三.解答题(共10小题)
21.下列代数式中的哪些是单项式,哪些是多项式,哪些是整式?
,4xy,,,x2+x,0,,m,﹣2.01×105
整式集合:{ …}
单项式集合:{ …}
多项式集合:{ …}.
22.已知x2y|a|+(b+2)是关于x、y的五次单项式,求a2﹣3ab的值.
23.观察下列一串单项式的特点:xy,﹣2x2y,4x3y,﹣8x4y,16x5y,…
(1)按此规律写出第9个单项式;
(2)试猜想第n个单项式为多少?它的系数和次数分别是多少?
24.观察下面有规律的三行单项式:
x,2x2,4x3,8x4,16x5,32x6,…①
﹣2x,4x2,﹣8x3,16x4,﹣32x5,64x6,…②
2x2,﹣3x3,5x4,﹣9x5,17x6,﹣33x7,…③
(1)根据你发现的规律,第一行第8个单项式为 ;
(2)第二行第n个单项式为 ;
(3)第三行第8个单项式为 ;第n个单项式为 .
25.已知有理数a和b满足多项式A.A=(a﹣1)x5+x|b+2|﹣2x2+bx+b是关于x的二次三项式.当x<﹣7时,化简:|x﹣a|+|x﹣b|
26.对于多项式(n﹣1)xm+2﹣3x2+2x(m,n为常数,且m是大于﹣2的整数).
(1)若n=2,且该多项式是关于x的三次三项式,求m的值;
(2)若该多项式化简后是关于x的二次单项式,求m,n的值;
(3)若该多项式是关于x的二次二项式,则m,n要满足什么条件?
27.如图,四边形ABCD和ECGF都是正方形.
(1)写出表示阴影部分面积的代数式;(结果要求化简)
(2)当a=4时,求阴影部分的面积.
28.已知图甲是一个长为2m,宽为2n的长方形,沿图甲中虚线用剪刀均匀分成四小块长方形,然后按图乙的形状拼成一个正方形.
(1)图乙中阴影部分正方形的边长为 (用含字母m,n的整式表示).
(2)请用两种不同的方法求图乙中阴影部分的面积.
方法一: ;
方法二: .
(3)观察图乙,并结合(2)中的结论,你能写出下列三个整式:(m+n)2,(m﹣n)2,mn之间的等量关系吗?
(4)根据(3)题中的等量关系,解决如下问题:若a+b=9,ab=5,求(a﹣b)2的值.
29.窗户的形状如图所示(图中长度单位:cm),其上部是半圆形,下部是边长相同的四个小正方形,已知下部小正方形的边长是acm,计算:
(1)窗户的面积;
(2)窗户的外框的总长.
30.把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面长为8,宽为7的长方形盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示设图中小长方形的宽为m.
(1)小长方形的长为 (用含m的代数式表示);
(2)求图②中两块阴影部分周长的和.
3.2代数式(同步练习解析)
一.选择题(共10小题)
1.单项式﹣3πxy2z3的系数和次数分别是( )
A.﹣π,5 B.﹣1,6 C.﹣3π,6 D.﹣3,7
【解答】解:根据单项式系数、次数的定义,单项式﹣3πxy2z3的系数和次数分别是﹣3π,6.
故选:C.
2.下列语句中错误的是( )
A.数字0也是单项式
B.单项式﹣a的系数与次数都是1
C.xy是二次单项式
D.的系数是
【解答】解:单独的一个数字也是单项式,故A正确;
单项式﹣a的系数应是﹣1,次数是1,故B错误;
xy的次数是2,符合单项式的定义,故C正确;
的系数是,故D正确.
故选:B.
3.若关于x,y的多项式化简后不含二次项,则m=( )
A. B. C. D.0
【解答】解:∵原式x2y+(6﹣7m)xyy3,
若不含二次项,即6﹣7m=0,
解得m.
故选:B.
4.若多项式3x|m|+(m﹣2)x+1是关于x的二次三项式,则m的值( )
A.2或﹣2 B.2 C.﹣2 D.﹣4
【解答】解:因为多项式3x|m|+(m﹣2)x+1是关于x的二次三项式,
所以|m|=2,且m﹣2≠0,
解得m=±2,且m≠2,
则m的值为﹣2.
故选:C.
5.下列说法中,正确的是( )
A.单项式xy2的系数是x
B.单项式﹣5x2的次数为﹣5
C.多项式x2+2x+18是二次三项式
D.多项式x2+y2﹣1的常数项是1
【解答】解:A、单项式xy2的系数是,原说法错误,故此选项不符合题意;
B、单项式﹣5x2的次数为2,原说法错误,故此选项不符合题意;
C、多项式x2+2x+18是二次三项式,原说法正确,故此选项符合题意;
D、多项式x2+y2﹣1的常数项是﹣1,原说法错误,故此选项不符合题意,
故选:C.
6.在式子,2πx2y,,y2﹣5,π+6,中,多项式的个数是( )
A.1 B.2 C.3 D.4
【解答】解:在式子,2πx2y,,y2﹣5,π+6,中,
多项式有:,y2﹣5,共2个.
故选:B.
7.下列代数式:(1)mn,(2)m,(3),(4),(5)2m+1,(6),(7),(8)x2+2x,(9)y3﹣5y中,整式有( )
A.3个 B.4个 C.6个 D.7个
【解答】解:根据整式的概念可知,整式有:
(1)mn;(2)m;(3);(5)2m+1;(6);(8)x2+2x.共6个.
故选:C.
8.在代数式a+b,x2,,﹣m,0,,中,单项式的个数是( )
A.6 B.5 C.4 D.3
【解答】解:x2,﹣m,0是单项式,
故选:D.
9.某九年级学生复习了整式有关概念后,他用一个圆代表所有代数式,画了下列图形来表示整式,多项式,单项式的关系,正确的是( )
【解答】解:代数式包括整式和分式,整式包括多项式和单项式,故正确的是选项D,
故选:D.
10.下面每个表格中的四个数都是按相同规律填写的:
根据此规律确定x的值为( )
A.135 B.170 C.209 D.252
【解答】解:∵a+(a+2)=20,
∴a=9,
∵b=a+1,
∴b=a+1=9+1=10,
∴x=20b+a
=20×10+9
=200+9
=209
故选:C.
二.填空题(共10小题)
11.单项式的系数是 .
【解答】解:单项式的系数是,
故答案为:.
12.如果一个单项式的系数和次数分别为m、n,那么2mn= ﹣2 .
【解答】解:由题意可知:m,n=3,
∴2mn=2×()×3=﹣2.
故答案为:﹣2.
13.把多项式2m3﹣m2n2+3﹣5m按字母m的升幂排列是 +3﹣5m﹣m2n2+2m3 .
【解答】解:把多项式2m3﹣m2n2+3﹣5m按字母m的升幂排列是+3﹣5m﹣m2n2+2m3.
故答案为:+3﹣5m﹣m2n2+2m3.
14.多项式3x2y﹣7x4y2﹣xy3+28是 六 次 四 项式,最高次项的系数是 ﹣7 .
【解答】解:多项式3x2y﹣7x4y2﹣xy3+28是六次四项式,最高次项的系数是﹣7.
故答案为六、四、﹣7
15.多项式x+7是关于x的二次三项式,则m= 2 .
【解答】解:∵多项式是关于x的二次三项式,
∴|m|=2,
∴m=±2,
但﹣(m+2)≠0,
即m≠﹣2,
综上所述,m=2,故填空答案:2.
16.多项式x|m|﹣(m﹣3)x+6是关于x的三次三项式,则m的值是 ﹣3 .
【解答】解:∵多项式是关于x的三次三项式,
∴|m|=3,
∴m=±3,
但m﹣3≠0,
即m≠3,
综上所述m=﹣3.
故答案为:﹣3.
17.已知关于x的多项式(m﹣2)x2﹣mx+3中的x的一次项系数为﹣2,则这个多项式是 一 次 二 项式.
【解答】解:∵多项式(m﹣2)x2﹣mx+3中的x的一次项系数为﹣2,∴﹣m=﹣2,m=2,
把m=2代入多项式(m﹣2)x2﹣mx+3中,m﹣2=0,∴二次项系数为0,多项式为一次二项式.
18.若单项式﹣x3yn+5的系数是m,次数是9,则m+n的值为 0 .
【解答】解:根据题意得:m=﹣1,3+n+5=9,
解得:m=﹣1,n=1,
则m+n=﹣1+1=0.
故答案为:0.
19.若代数式6amb4是六次单项式.则m= 2 .
【解答】解:若代数式6amb4是六次单项式,则m=2.
故答案为:2.
20.若多项式(k﹣1)x2+3x|k+2|+2为三次三项式,则k的值为 ﹣5 .
【解答】解:∵多项式(k﹣1)x2+3x|k+2|+2是关于x的三次三项式,
∴|k+2|=3,k﹣1≠0,
解得:k=﹣5.
故答案为:﹣5.
三.解答题(共10小题)
21.下列代数式中的哪些是单项式,哪些是多项式,哪些是整式?
,4xy,,,x2+x,0,,m,﹣2.01×105
整式集合:{ ,4xy,,0,m,﹣2.01×105 …}
单项式集合:{ 4xy,,0,m,﹣2.01×105 …}
多项式集合:{ …}.
【解答】解:整式集合:{,4xy,,0,m,﹣2.01×105 …};
单项式集合:{ 4xy,,0,m,﹣2.01×105 …};
多项式集合:{ …}.
故答案为:{,4xy,,0,m,﹣2.01×105 …};{ 4xy,,0,m,﹣2.01×105 …};{ …}.
22.已知x2y|a|+(b+2)是关于x、y的五次单项式,求a2﹣3ab的值.
【解答】解:∵x2y|a|+(b+2)是关于x,y的五次单项式,
∴,
解得:,
则当a=﹣3,b=﹣2时,a2﹣3ab=9﹣18=﹣9;
当a=3,b=﹣2时,a2﹣3ab=9+18=27.
23.观察下列一串单项式的特点:xy,﹣2x2y,4x3y,﹣8x4y,16x5y,…
(1)按此规律写出第9个单项式;
(2)试猜想第n个单项式为多少?它的系数和次数分别是多少?
【解答】解:(1)∵当n=1时,xy,
当n=2时,﹣2x2y,
当n=3时,4x3y,
当n=4时,﹣8x4y,
当n=5时,16x5y,
∴第9个单项式是29﹣1x9y,即256x9y.
(2)∴n为偶数时,单项式为负数.x的指数为n时,2的指数为n﹣1,
∴当n为奇数时的单项式为2n﹣1xny,
该单项式为(﹣1)n+12n﹣1xny
它的系数是(﹣1)n+12n﹣1,次数是n+1.
24.观察下面有规律的三行单项式:
x,2x2,4x3,8x4,16x5,32x6,…①
﹣2x,4x2,﹣8x3,16x4,﹣32x5,64x6,…②
2x2,﹣3x3,5x4,﹣9x5,17x6,﹣33x7,…③
(1)根据你发现的规律,第一行第8个单项式为 128x8 ;
(2)第二行第n个单项式为 (﹣2)nxn ;
(3)第三行第8个单项式为 ﹣129x9 ;第n个单项式为 (﹣1)n+1(1+2n﹣1)xn+1 .
【解答】解:(1)因为第一行的每个单项式,数字因数后面都是前面的2倍,字母次数与这个单项式是第几个有关,根据这个规律可得第一行第8个单项式为 128x8;
(2)因为第二行的每个单项式,数字因数后面都是前面的(﹣2)倍,字母次数与这个单项式是第几个有关,根据这个规律可得第n个单项式为 (﹣2)nxn;
(3)通过观察第三行的这组单项式,这组单项式符合 (﹣1)n+1(1+2n﹣1)xn+1,第8个单项式是﹣129x9;第n个单项式为 (﹣1)n+1(1+2n﹣1)xn+1.
故答案为:(1)128x8,(2)(﹣2x)n,(3)﹣129x9 ,(﹣1)n+1(1+2n﹣1)xn+1
25.已知有理数a和b满足多项式A.A=(a﹣1)x5+x|b+2|﹣2x2+bx+b是关于x的二次三项式.当x<﹣7时,化简:|x﹣a|+|x﹣b|
【解答】解:∵有理数a和b满足多项式A.A=(a﹣1)x5+x|b+2|﹣2x2+bx+b是关于x的二次三项式,
∴a﹣1=0,解得a=1.
当|b+2|=2时,解得b=0,此时A不是二次三项式;或b=﹣4,此时A是关于x的二次三项式,
当|b+2|=1时,解得b=﹣1或b=﹣3,
当|b+2|=0时,解得b=﹣2,
当5次项和|b+2|是同类项,并且系数互为相反数时,a=0,b=3或﹣7,
∴当a=1,b=﹣1,x<﹣7时,不是二次三项式;
当a=1,b=﹣2,x<﹣7时,|x﹣a|+|x﹣b|=|x﹣1|+|x+2|=1﹣x﹣x﹣2=﹣2x﹣1
当a=1,b=﹣3,x<﹣7时,|x﹣a|+|x﹣b|=|x﹣1|+|x+3|=1﹣x﹣x﹣3=﹣2x﹣2;
当a=1,b=﹣4,x<﹣7时,|x﹣a|+|x﹣b|=|x﹣1|+|x+4|=1﹣x﹣x﹣4=﹣2x﹣3;
当a=0,b=3,x<﹣7时,|x﹣a|+|x﹣b|=|x|+|x﹣3|=﹣x﹣x+3=﹣2x+3;
当a=0,b=﹣7,x<﹣7时,|x﹣a|+|x﹣b|=|x|+|x+7|=﹣x﹣x﹣7=﹣2x﹣7.
26.对于多项式(n﹣1)xm+2﹣3x2+2x(m,n为常数,且m是大于﹣2的整数).
(1)若n=2,且该多项式是关于x的三次三项式,求m的值;
(2)若该多项式化简后是关于x的二次单项式,求m,n的值;
(3)若该多项式是关于x的二次二项式,则m,n要满足什么条件?
【解答】解:(1)当n=2时,且该多项式是关于x的三次三项式,
故原式=xm+2﹣3x2+2x,m+2=3,解得:m=1;
(2)若该多项式是关于x的二次单项式,
则m+2=1,n﹣1=﹣2,
解得:m=﹣1,n=﹣1;
(3)若该多项式是关于x的二次二项式,
①n﹣1=0,m是大于﹣2的整数.
则m,n要满足的条件是:n=1,m是大于﹣2的整数;
②当m=﹣1时,n≠﹣1,
③m=0时,n≠4.
27.如图,四边形ABCD和ECGF都是正方形.
(1)写出表示阴影部分面积的代数式;(结果要求化简)
(2)当a=4时,求阴影部分的面积.
【解答】解:(1)S=a2+62a2(a+6)6=a2+62a2a×662a2﹣3a+18.
(2)当a=4cm,S42﹣3×4+18=14.
28.已知图甲是一个长为2m,宽为2n的长方形,沿图甲中虚线用剪刀均匀分成四小块长方形,然后按图乙的形状拼成一个正方形.
(1)图乙中阴影部分正方形的边长为 m﹣n (用含字母m,n的整式表示).
(2)请用两种不同的方法求图乙中阴影部分的面积.
方法一: (m+n)2﹣4mn ;
方法二: (m﹣n)2 .
(3)观察图乙,并结合(2)中的结论,你能写出下列三个整式:(m+n)2,(m﹣n)2,mn之间的等量关系吗?
(4)根据(3)题中的等量关系,解决如下问题:若a+b=9,ab=5,求(a﹣b)2的值.
【解答】解:(1)图乙中阴影部分正方形的边长为m﹣n;
(2)方法一:(m+n)2﹣4mn;
方法二:(m﹣n)2;
(3)(m+n)2﹣4mn=(m﹣n)2;
(4)(a﹣b)2=(a+b)2﹣4ab,
∵a+b=9,ab=5,
∴(a﹣b)2=81﹣20=61.
故答案为:m﹣n;(m+n)2﹣4mn;(m﹣n)2.
29.窗户的形状如图所示(图中长度单位:cm),其上部是半圆形,下部是边长相同的四个小正方形,已知下部小正方形的边长是acm,计算:
(1)窗户的面积;
(2)窗户的外框的总长.
【解答】解:(1)窗户的面积是:
4a2+πa2÷2
=4a2+0.5πa2
=(4+0.5π)a2(cm2)
(2)窗户的外框的总长是:
2a×3+πa
=6a+πa
=(6+π)a(cm)
30.把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面长为8,宽为7的长方形盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示设图中小长方形的宽为m.
(1)小长方形的长为 8﹣2m (用含m的代数式表示);
(2)求图②中两块阴影部分周长的和.
【解答】解:(1)小长方形的长为8﹣2m.
故答案为:8﹣2m;
(2)设小长方形卡片的长为n,
则右上小长方形周长为2×(8﹣n+7﹣n)=30﹣4n,
左下小长方形周长为2×(n+7﹣2m)=2n+14﹣4m,
∴两块阴影部分周长和=30﹣4n+2n+14﹣4m=44﹣2(n+2m)
∵8=n+2m,
∴两块阴影部分周长和=44﹣16=28.
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
