2022-2023学年北师大版九年级数学上册 第4章图形的相似 选择题专题训练(Word版含答案)
文档属性
| 名称 | 2022-2023学年北师大版九年级数学上册 第4章图形的相似 选择题专题训练(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 249.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-27 08:05:52 | ||
图片预览

文档简介
2022-2023学年北师大版九年级数学上册《第4章图形的相似》选择题专题训练(附答案)
1.若,则的值为( )
A. B.﹣ C. D.
2.下列各组的四条线段a,b,c,d是成比例线段的是( )
A.a=4,b=6,c=5,d=10 B.a=1,b=2,c=3,d=4
C.,b=3,c=2, D.a=2,,,
3.若(3b+d﹣2f≠0),则的值是( )
A.1 B. C.3 D.无法确定
4.如图,在△ABC中,D,E分别是AB,AC上的点,DE∥BC.若AD=6,BD=3,AE=8,则EC的长是( )
A.4 B.2 C.5 D.
5.如图,已知点A(0,4)、B(4,1),BC⊥x轴于点C,点P为线段OC上一点,且PA⊥PB.则点P的坐标为( )
A.(1,0) B.(1.5,0) C.(1.8,0) D.(2,0)
6.如图,在平面直角坐标系中,已知A(1,0),B(2,1),D(3,0),△ABC与△DEF位似,原点O是位似中心,则E点的坐标是( )
A.(7,4) B.(7,3) C.(6,4) D.(6,3)
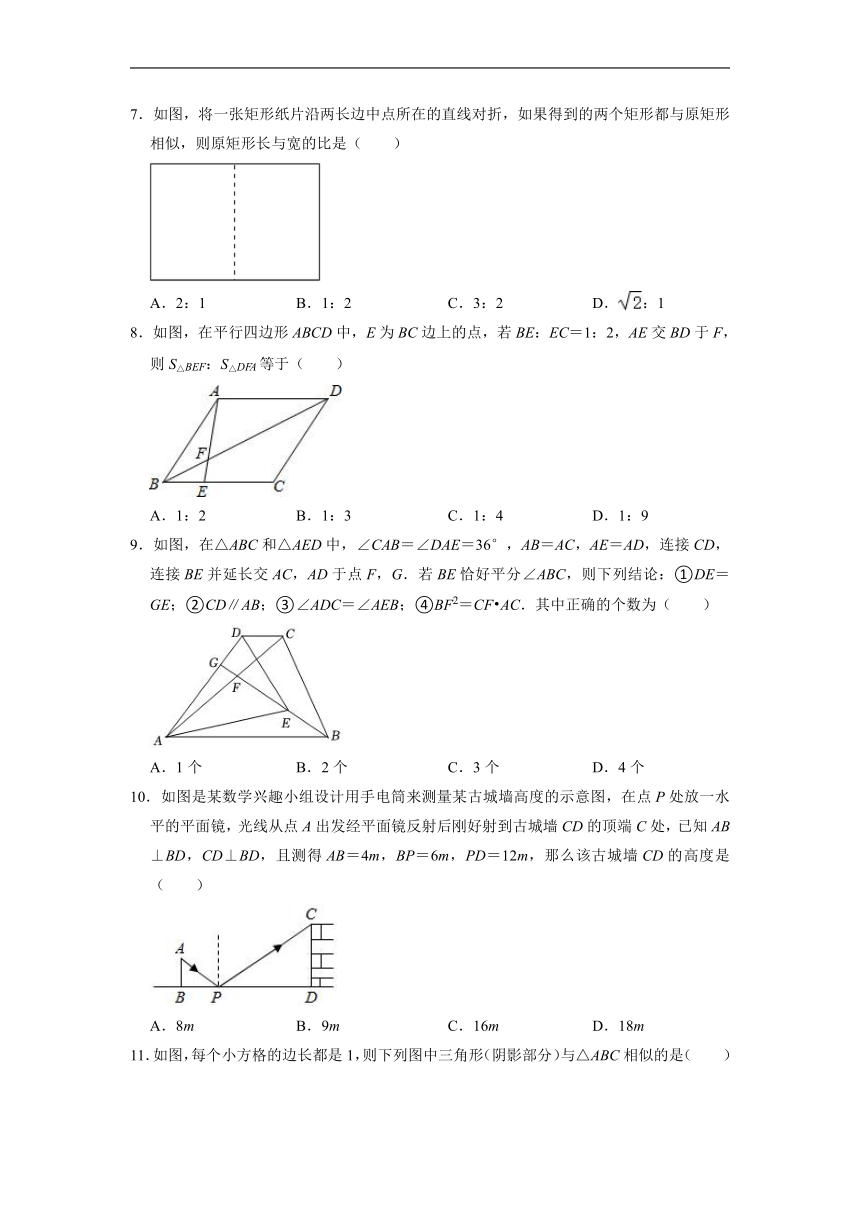
7.如图,将一张矩形纸片沿两长边中点所在的直线对折,如果得到的两个矩形都与原矩形相似,则原矩形长与宽的比是( )
A.2:1 B.1:2 C.3:2 D.:1
8.如图,在平行四边形ABCD中,E为BC边上的点,若BE:EC=1:2,AE交BD于F,则S△BEF:S△DFA等于( )
A.1:2 B.1:3 C.1:4 D.1:9
9.如图,在△ABC和△AED中,∠CAB=∠DAE=36°,AB=AC,AE=AD,连接CD,连接BE并延长交AC,AD于点F,G.若BE恰好平分∠ABC,则下列结论:①DE=GE;②CD∥AB;③∠ADC=∠AEB;④BF2=CF AC.其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
10.如图是某数学兴趣小组设计用手电筒来测量某古城墙高度的示意图,在点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=4m,BP=6m,PD=12m,那么该古城墙CD的高度是( )
A.8m B.9m C.16m D.18m
11.如图,每个小方格的边长都是1,则下列图中三角形(阴影部分)与△ABC相似的是( )
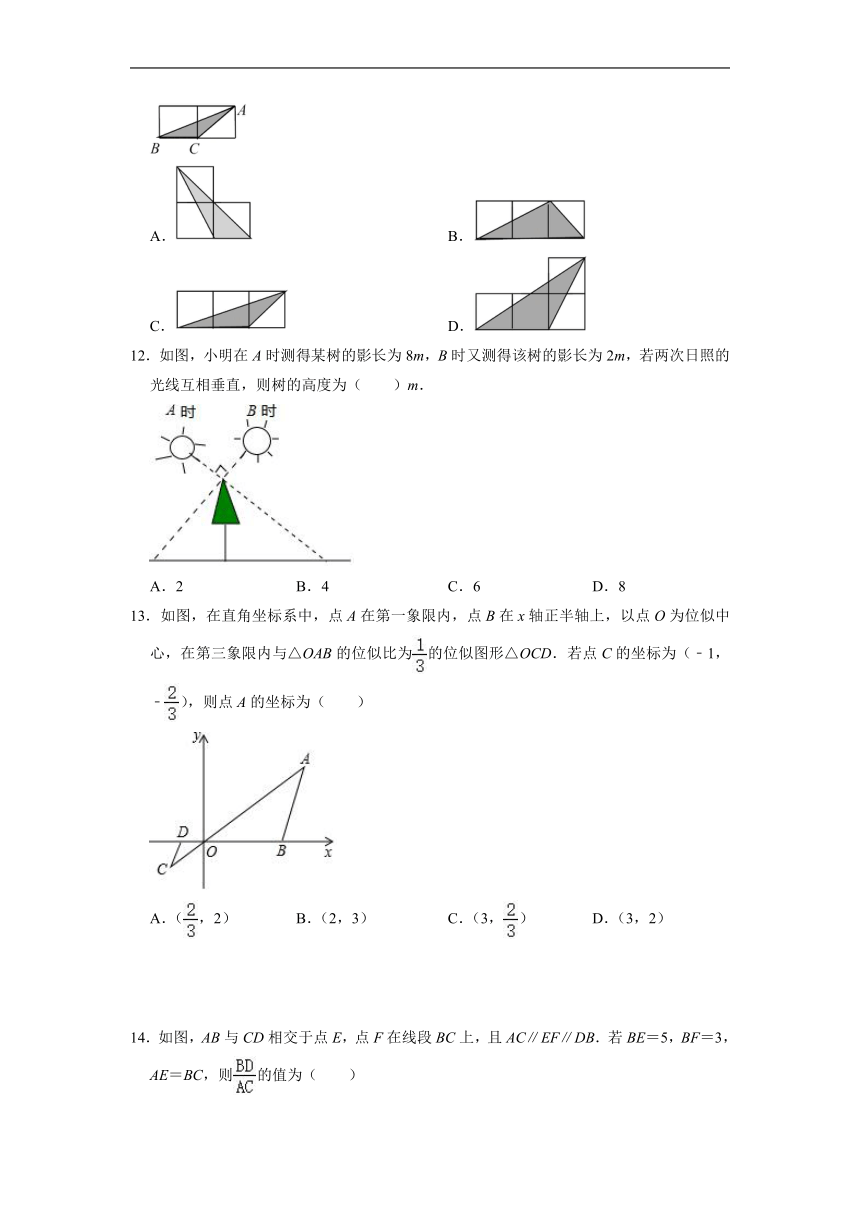
A. B.
C. D.
12.如图,小明在A时测得某树的影长为8m,B时又测得该树的影长为2m,若两次日照的光线互相垂直,则树的高度为( )m.
A.2 B.4 C.6 D.8
13.如图,在直角坐标系中,点A在第一象限内,点B在x轴正半轴上,以点O为位似中心,在第三象限内与△OAB的位似比为的位似图形△OCD.若点C的坐标为(﹣1,﹣),则点A的坐标为( )
A.(,2) B.(2,3) C.(3,) D.(3,2)
14.如图,AB与CD相交于点E,点F在线段BC上,且AC∥EF∥DB.若BE=5,BF=3,AE=BC,则的值为( )
A. B. C. D.
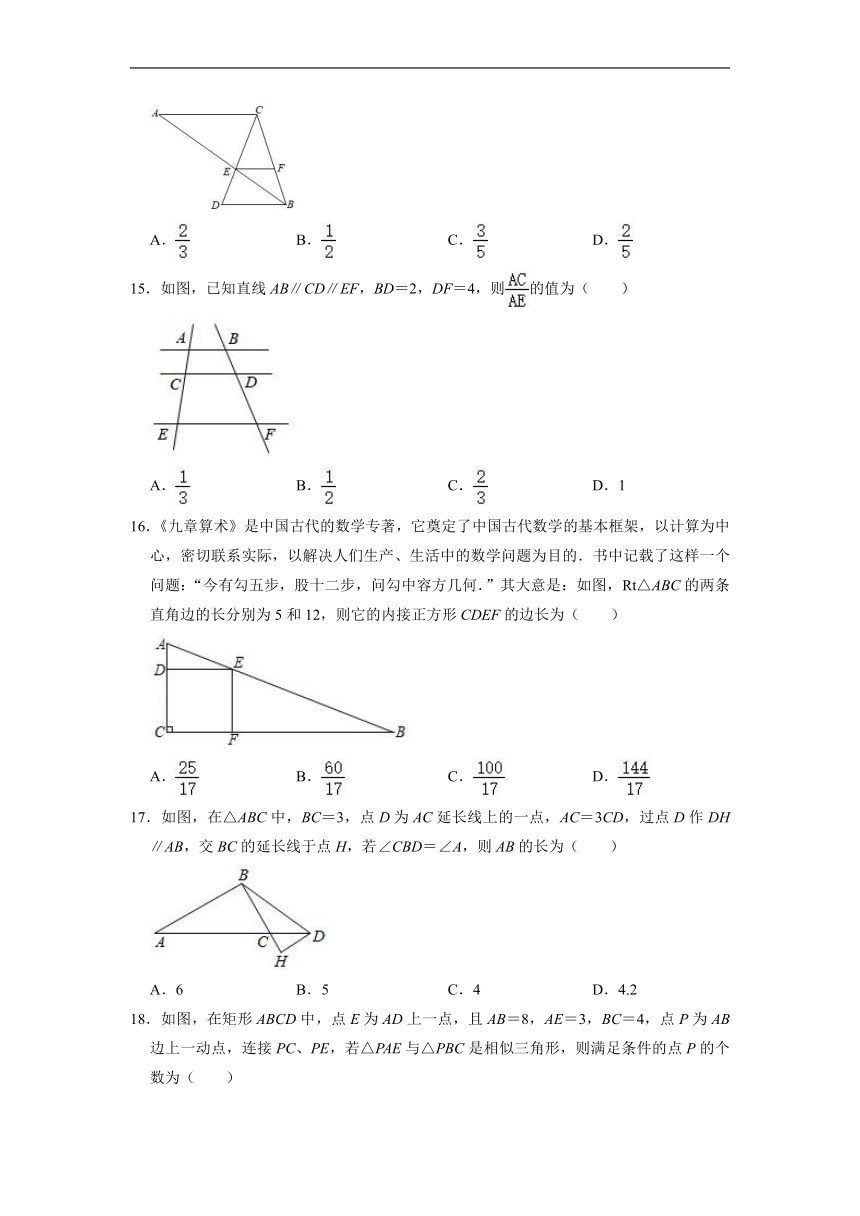
15.如图,已知直线AB∥CD∥EF,BD=2,DF=4,则的值为( )
A. B. C. D.1
16.《九章算术》是中国古代的数学专著,它奠定了中国古代数学的基本框架,以计算为中心,密切联系实际,以解决人们生产、生活中的数学问题为目的.书中记载了这样一个问题:“今有勾五步,股十二步,问勾中容方几何.”其大意是:如图,Rt△ABC的两条直角边的长分别为5和12,则它的内接正方形CDEF的边长为( )
A. B. C. D.
17.如图,在△ABC中,BC=3,点D为AC延长线上的一点,AC=3CD,过点D作DH∥AB,交BC的延长线于点H,若∠CBD=∠A,则AB的长为( )
A.6 B.5 C.4 D.4.2
18.如图,在矩形ABCD中,点E为AD上一点,且AB=8,AE=3,BC=4,点P为AB边上一动点,连接PC、PE,若△PAE与△PBC是相似三角形,则满足条件的点P的个数为( )
A.1 B.2 C.3 D.4
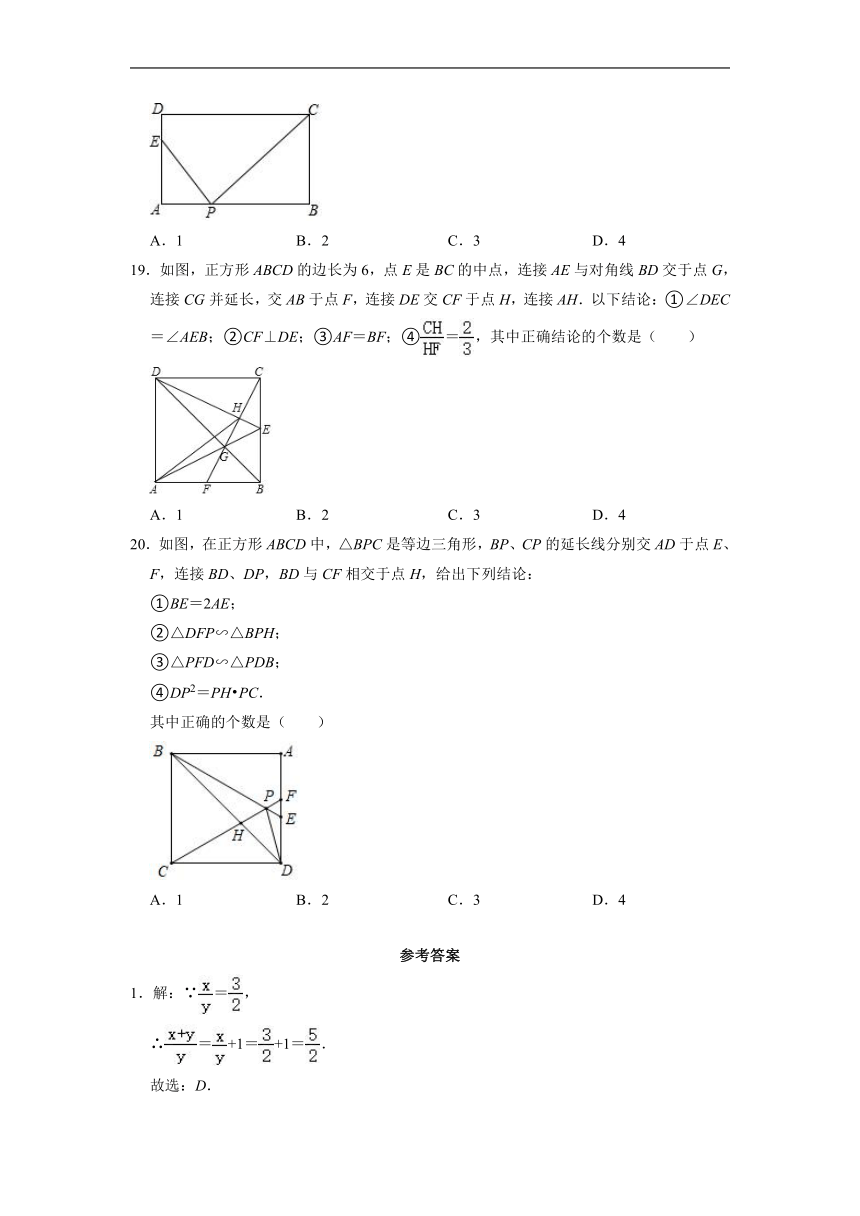
19.如图,正方形ABCD的边长为6,点E是BC的中点,连接AE与对角线BD交于点G,连接CG并延长,交AB于点F,连接DE交CF于点H,连接AH.以下结论:①∠DEC=∠AEB;②CF⊥DE;③AF=BF;④=,其中正确结论的个数是( )
A.1 B.2 C.3 D.4
20.如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论:
①BE=2AE;
②△DFP∽△BPH;
③△PFD∽△PDB;
④DP2=PH PC.
其中正确的个数是( )
A.1 B.2 C.3 D.4
参考答案
1.解:∵=,
∴=+1=+1=.
故选:D.
2.解:A.4×10≠6×5,故不符合题意,
B.1×4≠2×3,故不符合题意,
C.≠2×3,故不符合题意,
D.,故符合题意,
故选:D.
3.解:∵(3b+d﹣2f≠0),
∴a=3b,c=3d,e=3f,
∴===3.
故选:C.
4.解:∵DE∥BC,
∴,即,
解得,EC=4,
故选:A.
5.解:如图所示:
∵PA⊥PB,
∴∠2+∠3=90°.
∵AO⊥x轴,
∴∠1=∠2.
又∵BC⊥x轴,AO⊥x轴,
∴∠BCP=∠POA=90°.
∴△BCP∽△POA.
∴=.
∵点A(0,4)、B(4,1),
∴AO=4,BC=1,OC=4,
∴=,
解得OP=2.
∴P(2,0).
故选:D.
6.解:∵A(1,0),D(3,0),
∴OA=1,OD=3,
∵△ABC与△DEF位似,
∴AB∥DE,
∴==,
∴△ABC与△DEF的位似比为1:3,
∵点B的坐标为(2,1),
∴E点的坐标为(2×3,1×3),即E点的坐标为(6,3),
故选:D.
7.解:设原来矩形的长为x,宽为y,
则对折后的矩形的长为y,宽为,
∵得到的两个矩形都和原矩形相似,
∴x:y=y:,
解得x:y=:1.
故选:D.
8.解:∵BE:EC=1:2,
∴设BE=x,则EC=2x,BC=3x,
∵四边形ABCD是平行四边形,
∴AD=BC=3x,AD∥BC,
∴△BEF∽△DAF,
∴=()2=,
故选D.
9.解:∵∠CAB=∠DAE=36°,
∴∠CAB﹣∠CAE=∠DAE﹣∠CAE,即∠DAC=∠EAB,
在△DAC和△EAB中,
,
∴△DAC≌△EAB(SAS),
∴∠ADC=∠AEB,
故③结论正确;
∵∠CAB=∠DAE=36°,
∴∠ACB=∠ABC=(180°﹣36°)÷2=72°,
∵BE平分∠ABC,
∴∠ABE=∠CBE=36°,
∴∠DCA=∠EBA=36°,∠CAB=36°,
∴CD∥AB(内错角相等,两直线平行),
故②结论正确;
假设DE=GE,则∠DGE=∠ADE=72°,∠DEG=180°﹣2×72°=36°,
∴∠AEG=∠AED﹣∠DEG=72°﹣36°=36°,
∵∠ABE=36°,
∴∠AEG=∠ABE,
∴AE∥AB(这与AE与AB交于A点矛盾),
∴假设不成立,
故①结论不正确;
∵∠FAB=∠FBA=∠CBF=36°,∠BCF=∠ACB,
∴△CBF∽△CAB,
∴,
∴BC2=CF AC
∵∠CBF=36°,∠FCB=72°,
∴∠BFC=72°,
∴BF=BF,
∴BF2=AC CF,
故④结论正确.
故选:C.
10.解:根据题意得∠APB=∠CPD,
∵AB⊥BD,CD⊥BD,
∴∠ABP=∠CDP=90°,
∴Rt△ABP∽Rt△CDP,
∴=,即=,
解得:CD=8.
答:该古城墙CD的高度为8m.
故选:A.
11.解:由勾股定理得:AB==,BC=1,AC==,
∴BC:AC:AB=1::,
A、三边之比为1:5:2,图中的三角形(阴影部分)与△ABC不相似,不符合题意;
B、三边之比:::3,图中的三角形(阴影部分)与△ABC不相似,不符合题意;
C、三边之比为:2:=1::,图中的三角形(阴影部分)与△ABC相似,符合题意;
D、三边之比为2::,图中的三角形(阴影部分)与△ABC不相似,不符合题意.
故选:C.
12.解:根据题意,作△EFC,树高为CD,且∠ECF=90°,ED=2m,FD=8m;
∵∠E+∠F=90°,∠E+∠ECD=90°,
∴∠ECD=∠F,
∴△EDC∽△CDF,
∴=,即DC2=ED FD=2×8=16,
解得CD=4m.
故选:B.
13.解:∵以点O为位似中心,在第三象限内作与△OAB的位似比为的位似图形△OCD,C(﹣1,﹣),
∴点A的坐标为(﹣1×(﹣3),﹣×(﹣3)),即(3,2),
故选:D.
14.解:设CF=x,
∵EF∥AC,
∴=,
∴=,
解得x=,
∴CF=,
∵EF∥DB,
∴===.
故选:A.
15.解:∵AB∥CD∥EF,BD=2,DF=4,
∴===,
故选:A.
16.解:∵四边形CDEF是正方形,
∴CD=ED,DE∥CF,
设ED=x,则CD=x,AD=5﹣x,
∵DE∥CF,
∴∠ADE=∠C,∠AED=∠B,
∴△ADE∽△ACB,
∴=,
∴=,
∴x=,
∴正方形CDEF的边长为.
故选:B.
17.解:∵DH∥AB,
∴△ABC∽△DHC,
∴,
∵BC=3,AC=3CD,
∴CH=1.
∴BH=4,
∵∠CBD=∠A,∠ABC=∠BHD,
∴△ABC∽△BHD,
∴,
∵△ABC∽△DHC,
∴,
∴AB=3DH,
∴,
解得DH=2,
∴AB=3DH=3×2=6,
故选:A.
18.解:设AP=x,则BP=8﹣x,
当△PAE∽△PBC时,=,即=,
解得,x=,
当△PAE∽△CBP时,=,即=,
解得,x=2或6,
可得:满足条件的点P的个数有3个.
故选:C.
19.解:∵四边形ABCD是边长为6的正方形,点E是BC的中点,
∴AB=AD=BC=CD=6,BE=CE=3,∠DCE=∠ABE=90°,∠ABD=∠CBD=45°,
∴△ABE≌△DCE(SAS)
∴∠DEC=∠AEB,∠BAE=∠CDE,DE=AE,故①正确,
∵AB=BC,∠ABG=∠CBG,BG=BG,
∴△ABG≌△CBG(SAS)
∴∠BAE=∠BCF,
∴∠BCF=∠CDE,且∠CDE+∠CED=90°,
∴∠BCF+∠CED=90°,
∴∠CHE=90°,
∴CF⊥DE,故②正确,
∵∠CDE=∠BCF,DC=BC,∠DCE=∠CBF=90°,
∴△DCE≌△CBF(ASA),
∴CE=BF,
∵CE=BC=AB,
∴BF=AB,
∴AF=FB,故③正确,
③解法二:∵四边形ABCD是正方形,
∴BC∥AD,
∵E是BC的中点,
∴==,
∵AB∥CD,
∴==,
∵AB=CD,
∴BF=AB.
∵DC=6,CE=3,
∴DE===3,
∵S△DCE=×CD×CE=×DE×CH,
∴CH=,
∵∠CHE=∠CBF,∠BCF=∠ECH,
∴△ECH∽△FCB,
∴=,
∴CF==3,
∴HF=CF﹣CH=,
∴=,故④正确,
故选:D.
20.解:∵四边形ABCD是正方形,
∴∠A=∠CBA=90°,
∵△BCP是等边三角形,
∴∠PBC=∠PCB=∠BPC=60°,
∴∠ABE=30°,
∴BE=2AE,故①正确,
∵AD∥BC,
∴∠DFP=∠BCP=∠BPH=60°,
∵∠PHB=∠PCB+∠CBH=60°+45°=105°,
又∵CD=CP,∠PCD=30°,
∴∠CPD=∠CDP=75°,
∴∠DPF=105°,
∴∠PHB=∠DPF,
∴△DFP∽△BPH,故②正确,
∵∠DPB=60°+75°=135°≠∠DPF,
∴△PFD与△PDB不相似,故③错误,
∵∠PDH=∠PDC﹣∠CDH=75°﹣45°=30°,
∴∠PDH=∠PCD,
∵∠DPH=∠CPD,
∴△PDH∽△PCD,
∴=,
∴PD2=PH PC,故④正确,
故选:C.
1.若,则的值为( )
A. B.﹣ C. D.
2.下列各组的四条线段a,b,c,d是成比例线段的是( )
A.a=4,b=6,c=5,d=10 B.a=1,b=2,c=3,d=4
C.,b=3,c=2, D.a=2,,,
3.若(3b+d﹣2f≠0),则的值是( )
A.1 B. C.3 D.无法确定
4.如图,在△ABC中,D,E分别是AB,AC上的点,DE∥BC.若AD=6,BD=3,AE=8,则EC的长是( )
A.4 B.2 C.5 D.
5.如图,已知点A(0,4)、B(4,1),BC⊥x轴于点C,点P为线段OC上一点,且PA⊥PB.则点P的坐标为( )
A.(1,0) B.(1.5,0) C.(1.8,0) D.(2,0)
6.如图,在平面直角坐标系中,已知A(1,0),B(2,1),D(3,0),△ABC与△DEF位似,原点O是位似中心,则E点的坐标是( )
A.(7,4) B.(7,3) C.(6,4) D.(6,3)
7.如图,将一张矩形纸片沿两长边中点所在的直线对折,如果得到的两个矩形都与原矩形相似,则原矩形长与宽的比是( )
A.2:1 B.1:2 C.3:2 D.:1
8.如图,在平行四边形ABCD中,E为BC边上的点,若BE:EC=1:2,AE交BD于F,则S△BEF:S△DFA等于( )
A.1:2 B.1:3 C.1:4 D.1:9
9.如图,在△ABC和△AED中,∠CAB=∠DAE=36°,AB=AC,AE=AD,连接CD,连接BE并延长交AC,AD于点F,G.若BE恰好平分∠ABC,则下列结论:①DE=GE;②CD∥AB;③∠ADC=∠AEB;④BF2=CF AC.其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
10.如图是某数学兴趣小组设计用手电筒来测量某古城墙高度的示意图,在点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=4m,BP=6m,PD=12m,那么该古城墙CD的高度是( )
A.8m B.9m C.16m D.18m
11.如图,每个小方格的边长都是1,则下列图中三角形(阴影部分)与△ABC相似的是( )
A. B.
C. D.
12.如图,小明在A时测得某树的影长为8m,B时又测得该树的影长为2m,若两次日照的光线互相垂直,则树的高度为( )m.
A.2 B.4 C.6 D.8
13.如图,在直角坐标系中,点A在第一象限内,点B在x轴正半轴上,以点O为位似中心,在第三象限内与△OAB的位似比为的位似图形△OCD.若点C的坐标为(﹣1,﹣),则点A的坐标为( )
A.(,2) B.(2,3) C.(3,) D.(3,2)
14.如图,AB与CD相交于点E,点F在线段BC上,且AC∥EF∥DB.若BE=5,BF=3,AE=BC,则的值为( )
A. B. C. D.
15.如图,已知直线AB∥CD∥EF,BD=2,DF=4,则的值为( )
A. B. C. D.1
16.《九章算术》是中国古代的数学专著,它奠定了中国古代数学的基本框架,以计算为中心,密切联系实际,以解决人们生产、生活中的数学问题为目的.书中记载了这样一个问题:“今有勾五步,股十二步,问勾中容方几何.”其大意是:如图,Rt△ABC的两条直角边的长分别为5和12,则它的内接正方形CDEF的边长为( )
A. B. C. D.
17.如图,在△ABC中,BC=3,点D为AC延长线上的一点,AC=3CD,过点D作DH∥AB,交BC的延长线于点H,若∠CBD=∠A,则AB的长为( )
A.6 B.5 C.4 D.4.2
18.如图,在矩形ABCD中,点E为AD上一点,且AB=8,AE=3,BC=4,点P为AB边上一动点,连接PC、PE,若△PAE与△PBC是相似三角形,则满足条件的点P的个数为( )
A.1 B.2 C.3 D.4
19.如图,正方形ABCD的边长为6,点E是BC的中点,连接AE与对角线BD交于点G,连接CG并延长,交AB于点F,连接DE交CF于点H,连接AH.以下结论:①∠DEC=∠AEB;②CF⊥DE;③AF=BF;④=,其中正确结论的个数是( )
A.1 B.2 C.3 D.4
20.如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论:
①BE=2AE;
②△DFP∽△BPH;
③△PFD∽△PDB;
④DP2=PH PC.
其中正确的个数是( )
A.1 B.2 C.3 D.4
参考答案
1.解:∵=,
∴=+1=+1=.
故选:D.
2.解:A.4×10≠6×5,故不符合题意,
B.1×4≠2×3,故不符合题意,
C.≠2×3,故不符合题意,
D.,故符合题意,
故选:D.
3.解:∵(3b+d﹣2f≠0),
∴a=3b,c=3d,e=3f,
∴===3.
故选:C.
4.解:∵DE∥BC,
∴,即,
解得,EC=4,
故选:A.
5.解:如图所示:
∵PA⊥PB,
∴∠2+∠3=90°.
∵AO⊥x轴,
∴∠1=∠2.
又∵BC⊥x轴,AO⊥x轴,
∴∠BCP=∠POA=90°.
∴△BCP∽△POA.
∴=.
∵点A(0,4)、B(4,1),
∴AO=4,BC=1,OC=4,
∴=,
解得OP=2.
∴P(2,0).
故选:D.
6.解:∵A(1,0),D(3,0),
∴OA=1,OD=3,
∵△ABC与△DEF位似,
∴AB∥DE,
∴==,
∴△ABC与△DEF的位似比为1:3,
∵点B的坐标为(2,1),
∴E点的坐标为(2×3,1×3),即E点的坐标为(6,3),
故选:D.
7.解:设原来矩形的长为x,宽为y,
则对折后的矩形的长为y,宽为,
∵得到的两个矩形都和原矩形相似,
∴x:y=y:,
解得x:y=:1.
故选:D.
8.解:∵BE:EC=1:2,
∴设BE=x,则EC=2x,BC=3x,
∵四边形ABCD是平行四边形,
∴AD=BC=3x,AD∥BC,
∴△BEF∽△DAF,
∴=()2=,
故选D.
9.解:∵∠CAB=∠DAE=36°,
∴∠CAB﹣∠CAE=∠DAE﹣∠CAE,即∠DAC=∠EAB,
在△DAC和△EAB中,
,
∴△DAC≌△EAB(SAS),
∴∠ADC=∠AEB,
故③结论正确;
∵∠CAB=∠DAE=36°,
∴∠ACB=∠ABC=(180°﹣36°)÷2=72°,
∵BE平分∠ABC,
∴∠ABE=∠CBE=36°,
∴∠DCA=∠EBA=36°,∠CAB=36°,
∴CD∥AB(内错角相等,两直线平行),
故②结论正确;
假设DE=GE,则∠DGE=∠ADE=72°,∠DEG=180°﹣2×72°=36°,
∴∠AEG=∠AED﹣∠DEG=72°﹣36°=36°,
∵∠ABE=36°,
∴∠AEG=∠ABE,
∴AE∥AB(这与AE与AB交于A点矛盾),
∴假设不成立,
故①结论不正确;
∵∠FAB=∠FBA=∠CBF=36°,∠BCF=∠ACB,
∴△CBF∽△CAB,
∴,
∴BC2=CF AC
∵∠CBF=36°,∠FCB=72°,
∴∠BFC=72°,
∴BF=BF,
∴BF2=AC CF,
故④结论正确.
故选:C.
10.解:根据题意得∠APB=∠CPD,
∵AB⊥BD,CD⊥BD,
∴∠ABP=∠CDP=90°,
∴Rt△ABP∽Rt△CDP,
∴=,即=,
解得:CD=8.
答:该古城墙CD的高度为8m.
故选:A.
11.解:由勾股定理得:AB==,BC=1,AC==,
∴BC:AC:AB=1::,
A、三边之比为1:5:2,图中的三角形(阴影部分)与△ABC不相似,不符合题意;
B、三边之比:::3,图中的三角形(阴影部分)与△ABC不相似,不符合题意;
C、三边之比为:2:=1::,图中的三角形(阴影部分)与△ABC相似,符合题意;
D、三边之比为2::,图中的三角形(阴影部分)与△ABC不相似,不符合题意.
故选:C.
12.解:根据题意,作△EFC,树高为CD,且∠ECF=90°,ED=2m,FD=8m;
∵∠E+∠F=90°,∠E+∠ECD=90°,
∴∠ECD=∠F,
∴△EDC∽△CDF,
∴=,即DC2=ED FD=2×8=16,
解得CD=4m.
故选:B.
13.解:∵以点O为位似中心,在第三象限内作与△OAB的位似比为的位似图形△OCD,C(﹣1,﹣),
∴点A的坐标为(﹣1×(﹣3),﹣×(﹣3)),即(3,2),
故选:D.
14.解:设CF=x,
∵EF∥AC,
∴=,
∴=,
解得x=,
∴CF=,
∵EF∥DB,
∴===.
故选:A.
15.解:∵AB∥CD∥EF,BD=2,DF=4,
∴===,
故选:A.
16.解:∵四边形CDEF是正方形,
∴CD=ED,DE∥CF,
设ED=x,则CD=x,AD=5﹣x,
∵DE∥CF,
∴∠ADE=∠C,∠AED=∠B,
∴△ADE∽△ACB,
∴=,
∴=,
∴x=,
∴正方形CDEF的边长为.
故选:B.
17.解:∵DH∥AB,
∴△ABC∽△DHC,
∴,
∵BC=3,AC=3CD,
∴CH=1.
∴BH=4,
∵∠CBD=∠A,∠ABC=∠BHD,
∴△ABC∽△BHD,
∴,
∵△ABC∽△DHC,
∴,
∴AB=3DH,
∴,
解得DH=2,
∴AB=3DH=3×2=6,
故选:A.
18.解:设AP=x,则BP=8﹣x,
当△PAE∽△PBC时,=,即=,
解得,x=,
当△PAE∽△CBP时,=,即=,
解得,x=2或6,
可得:满足条件的点P的个数有3个.
故选:C.
19.解:∵四边形ABCD是边长为6的正方形,点E是BC的中点,
∴AB=AD=BC=CD=6,BE=CE=3,∠DCE=∠ABE=90°,∠ABD=∠CBD=45°,
∴△ABE≌△DCE(SAS)
∴∠DEC=∠AEB,∠BAE=∠CDE,DE=AE,故①正确,
∵AB=BC,∠ABG=∠CBG,BG=BG,
∴△ABG≌△CBG(SAS)
∴∠BAE=∠BCF,
∴∠BCF=∠CDE,且∠CDE+∠CED=90°,
∴∠BCF+∠CED=90°,
∴∠CHE=90°,
∴CF⊥DE,故②正确,
∵∠CDE=∠BCF,DC=BC,∠DCE=∠CBF=90°,
∴△DCE≌△CBF(ASA),
∴CE=BF,
∵CE=BC=AB,
∴BF=AB,
∴AF=FB,故③正确,
③解法二:∵四边形ABCD是正方形,
∴BC∥AD,
∵E是BC的中点,
∴==,
∵AB∥CD,
∴==,
∵AB=CD,
∴BF=AB.
∵DC=6,CE=3,
∴DE===3,
∵S△DCE=×CD×CE=×DE×CH,
∴CH=,
∵∠CHE=∠CBF,∠BCF=∠ECH,
∴△ECH∽△FCB,
∴=,
∴CF==3,
∴HF=CF﹣CH=,
∴=,故④正确,
故选:D.
20.解:∵四边形ABCD是正方形,
∴∠A=∠CBA=90°,
∵△BCP是等边三角形,
∴∠PBC=∠PCB=∠BPC=60°,
∴∠ABE=30°,
∴BE=2AE,故①正确,
∵AD∥BC,
∴∠DFP=∠BCP=∠BPH=60°,
∵∠PHB=∠PCB+∠CBH=60°+45°=105°,
又∵CD=CP,∠PCD=30°,
∴∠CPD=∠CDP=75°,
∴∠DPF=105°,
∴∠PHB=∠DPF,
∴△DFP∽△BPH,故②正确,
∵∠DPB=60°+75°=135°≠∠DPF,
∴△PFD与△PDB不相似,故③错误,
∵∠PDH=∠PDC﹣∠CDH=75°﹣45°=30°,
∴∠PDH=∠PCD,
∵∠DPH=∠CPD,
∴△PDH∽△PCD,
∴=,
∴PD2=PH PC,故④正确,
故选:C.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
