2022-2023学年冀教版九年级数学上册25.4相似三角形的判定 同步达标测试题 (Word版含答案)
文档属性
| 名称 | 2022-2023学年冀教版九年级数学上册25.4相似三角形的判定 同步达标测试题 (Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 382.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-27 00:00:00 | ||
图片预览




文档简介
2022-2023学年冀教版九年级数学上册《25.4相似三角形的判定》同步达标测试题(附答案)
一.选择题(共5小题,满分20分)
1.如图,在△ABC中,高BD、CE相交于点F.图中与△AEC一定相似的三角形有( )
A.1个 B.2个 C.3个 D.4个
2.如图,在△ABC中,AB=AC,∠C的平分线交AB于点D,增添下列条件仍然不能判断△ABC∽△CBD的是( )
A.∠A=36° B.BC=DC C.BC2=BD AB D.∠B=∠ACB
3.如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是( )
A. B. C. D.
4.如图,在△ABC中,∠C=45°,将△ABC绕着点B逆时针方向旋转,使点C的对应点C'落在CA的延长线上,得到△A'BC',连接AA',交BC'于点O.下列结论:①∠AC'A'=90°;②AA'=BC';③∠A'BC'=∠A'AC';④△A'OC'∽△BOA.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
5.如图,在正方形网格中有5个格点三角形,分别是:①△ABC,②△ACD,③△ADE,④△AEF,⑤△AGH,其中与⑤相似的三角形是( )
A.①③ B.①④ C.②④ D.①③④
二.填空题(共9小题,满分36分)
6.如图,在△ABC中,∠ACB=90°,CD⊥AB,DE⊥BC,垂足分别为点D,E,则图中与△ABC相似的三角形个数有 个.
7.如图△ABC中,AB=8,AC=6,点D在AC上,AD=2,要在AB上找一E,使△ADE与△ABC相似,AE= .
8.如图,线段AB=9,AC⊥AB于点A,BD⊥AB于点B,AC=2,BD=4,点P为线段AB上一动点,且以A、C、P为顶点的三角形与以B、D、P为顶点的三角形相似,则AP的长为 .
9.如图,正方形ABCD的边长为4,AE=EB,MN=2,线段MN的两端在CB、CD上滑动,当CM= 时,△ADE与△CMN相似.
10.如图,一次函数y=﹣x+6的图象与x轴交于点B,与y轴交于点A,过线段AB的中点P(4,3)作一条直线与△AOB交于点Q,使得所截新三角形与△AOB相似,则点Q坐标是 .
11.如图,点E在线段AB上,CA⊥AB于点A,DB⊥AB于点B,AC=1,AB=5,EB=2,点P是射线BD上的一个动点,则当BP= 时,△CEA与△EPB相似.
12.如图,在矩形ABCD中,AB=10,AD=4,P是CD边上的一个动点,则当△ADP与△BCP相似时,DP= .
13.如图,AB、CD交于点O,且OC=45,OD=30,OB=36,当OA= 时,△AOC与△BOD相似.
14.如图,在矩形ABCD中,E,F分别是CD,BC上的点,∠AEF=90°,有以下结论:①△ADE∽△AEF;②△ECF∽△AEF;③△ADE∽△ECF;④△AEF∽△ABF;⑤△ADE∽△ABF,其中正确的是 (把你认为正确的序号都填上).
三.解答题(共8小题,满分64分)
15.如图,点D为△ABC边AB上一点,AD=2,BD=6,AC=4.求证:△ACD∽△ABC.
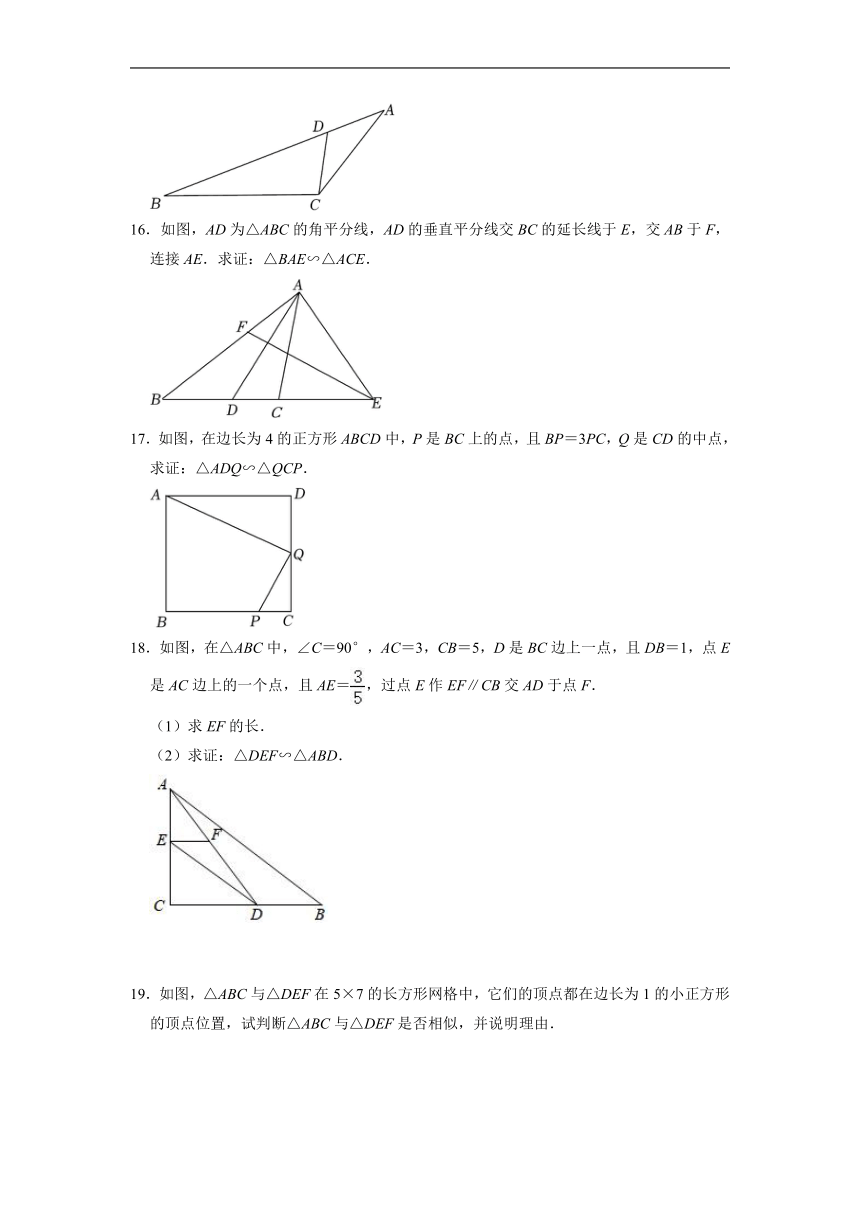
16.如图,AD为△ABC的角平分线,AD的垂直平分线交BC的延长线于E,交AB于F,连接AE.求证:△BAE∽△ACE.
17.如图,在边长为4的正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点,求证:△ADQ∽△QCP.
18.如图,在△ABC中,∠C=90°,AC=3,CB=5,D是BC边上一点,且DB=1,点E是AC边上的一个点,且AE=,过点E作EF∥CB交AD于点F.
(1)求EF的长.
(2)求证:△DEF∽△ABD.
19.如图,△ABC与△DEF在5×7的长方形网格中,它们的顶点都在边长为1的小正方形的顶点位置,试判断△ABC与△DEF是否相似,并说明理由.
20.如图,在四边形ABCD中,点E、F分别是AB、CD的中点,过点E作AB的垂线,过点F作CD的垂线,两垂线交于点G,联结AG、BG、CG、DG,且∠AGD=∠BGC.
(1)求证:AD=BC;
(2)求证:△AGD∽△EGF.
21.在△ABC中,AB=AC,∠BAC=120°,P为BC的中点,小明拿着含有30°角的透明直角三角板,使30°角的顶点落在点P上,三角板绕P点旋转.
(1)如图1,当三角板的一直角边和斜边分别与AB、BC交于点E、F时,连接EF,请说明△BPE∽△CFP;
(2)操作:将三角板绕点P旋转到图2情形时,三角板的两边分别交BA的延长线、边AC于点E、F,连接EF.
①探究1:△BPE与△CFP相似吗?请说明理由;
②探究2:△BPE与△PFE相似吗?请说明理由.
22.如图,点P是菱形ABCD的对角线BD上一点,连结CP并延长,交AD于E,交BA的延长线于点F.
(1)求证:PE PF=PC2.
(2)如图2,连接AC交BD于O,连接OE,若CE⊥BC,求证:△POC∽△AEC.
参考答案
一.选择题(共5小题,满分20分)
1.解:∵∠A=∠A,∠AEC=∠ADB=90°,
∴△AEC∽△ADB,
∴∠ACE=∠ABD,
又∵∠AEC=∠BEC=90°,
∴△AEC∽△FEB,
∵∠ACE=∠ACE,∠AEC=∠ADB=90°,
∴△AEC∽△FDC,
故选:C.
2.解:∵AB=AC,
∴∠ABC=∠ACB,
∵CD平分∠ACB,
∴∠ACD=∠BCD,
当∠A=36°时,
∴∠ABC=∠ACB=72°,
∴∠DCB=36°,
∴∠A=∠DCB,
又∵∠DBC=∠ABC,
∴△ABC∽△CBD,故选项A不符合题意;
当BC=DC时,
∴∠CDB=∠CBD,
∴∠ABC=∠ACB=∠CBD=∠CDB,
∴△ABC∽△CBD,故选项B不符合题意;
当BC2=BD AB时,
∴,
又∵∠CBD=∠ABC,
∴△ABC∽△CBD,故选项C不符合题意;
故选:D.
3.解:在△ABC中,∠ACB=135°,AC=,BC=2,
在B、C、D选项中的三角形都没有135°,而在A选项中,三角形的钝角为135°,它的两边分别为1和,
因为=,所以A选项中的三角形与△ABC相似.
故选:A.
4.解:∵将△ABC绕着点B逆时针方向旋转,
∴∠C=∠BC'A'=45°,∠CBC'=∠ABA',BC=BC',AB=BA',
∴∠C=∠BC'C=45°,
∴∠A'C'A=90°=∠CBC'=∠ABC',故①正确;
∴点A,点B,点A',点C'四点共圆,
∴AA'是直径,∠A'BC'=∠A'AC',故②错误,③正确,
∵点A,点B,点A',点C'四点共圆,
∴∠BC'A'=∠BAA',
又∵∠AOB=∠A'OC',
∴△AOB∽△A'OC',故④正确,
故选C.
5.解:由图形知,⑤中∠AHG=135°,
而①②③④中,只有①∠BAC=135°和③∠ADE=135°,
再根据两边成比例可判断,与⑤相似的三角形是①③,
故选:A.
二.填空题(共9小题,满分36分)
6.解:∵CD⊥AB,DE⊥BC,
∴∠CDA=∠CDB=∠DEB=∠DEC=90°=∠ACB,
∴∠A+∠B=90°=∠A+∠ACD=∠B+∠DCB=∠B+∠BDE=∠DCB+∠CDE,
∴∠A=∠BDE=∠BCD,∠B=∠ACD=∠CDE,
∴△ACB∽△ADC∽△DEB∽△CDB∽△CED,
故答案为:4.
7.解:∵∠A是公共角,
∴当,即时,△AED∽△ABC,
解得:AE=;
当,即时,△ADE∽△ABC,
解得:AE=,
故答案为:或
8.解:设AP=x.
∵以A、C、P为顶点的三角形与以B、D、P为顶点的三角形相似,
①当时,,解得x=3.
②当时,,解得x=1或8,
∴当以A、C、P为顶点的三角形与以B、D、P为顶点的三角形相似时,AP的长为1或3或8,
故答案为1或3或8.
9.解:∵AE=EB,
∴AD=2AE,
又∵△AED与以M、N、C为顶点的三角形相似,
∴分两种情况:
①CM与AD是对应边时,CM=2CN,
∴CM2+CN2=MN2=4,
即CM2+CM2=4,
解得:CM=;
②CM与AE是对应边时,CM=CN,
∴CM2+CN2=MN2=4,
即CM2+4CM2=4,
解得:CM=.
综上所述:当CM为或时,△AED与△CMN相似.
故答案是:或.
10.解:∵一次函数y=﹣x+6的图象与x轴交于点B,与y轴交于点A,
∴A(0,6),B(8,0),
∴OA=6,OB=8,AB===10,
如图有两种情形:①当PQ∥OB时,满足条件.
∵AP=PB,
∴AQ=OQ,
∴Q(0,3).
②当PQ′⊥AB时,满足条件.连接AQ′.
∵PA=PB,PQ′⊥AB,
∴Q′A=Q′B,设Q′A=Q′B=m,
在Rt△AOQ′中,则有m2=62+(8﹣m)2,
解得m=,
∴OQ′=8﹣=,
∴Q′(,0).
③当PQ∥y轴时,同法可得P(4,0).
综上所述,满足条件的点Q的坐标为(0,3)或(,0)或(4,0).
11.解:∵CA⊥AB,DB⊥AB,
∴∠A=∠B=90°,
又∵AB=5,EB=2,
∴AE=AB﹣EB=3,
①当△CAE∽△PBE时,=,即=,
解得:PB=;
②当△CAE∽△EBP时,=,即=,
解得:BP=6;
综上,当BP=或6时,△CEA与△EPB相似.
故答案为:或6.
12.解:①当△APD∽△PBC时,
=,即=,
解得:PD=2或PD=8;
②当△PAD∽△PBC时,
=,
即=,
解得:DP=5.
综上所述,DP的长度是2或8或5.
故答案是:2或8或5.
13.解:∵OC=45,OD=30,OB=36,△AOC∽△BOD,
∴,
即,解得OA=54;
若△AOC∽△DOB,
∴,
即,
解得OA=,
综上所述OA的长为54或.
故答案为:54或.
14.解:在矩形ABCD中,
∵∠D=∠C=90°,∠AEF=90°,
∴∠DEA+∠CEF=90°,∠DEA+∠DAE=90°,
∴∠DAE=∠CEF,
∴△ADE∽△ECF,
其余都不符合相似的条件.
故答案为:③.
三.解答题(共8小题,满分64分)
15.解:∵AD=2,BD=6,
∴AB=8,
∴,,
∴,
又∵∠A=∠A,
∴△ACD∽△ABC.
16.证明:∵AD是∠BAC的平分线,
∴∠BAD=∠CAD,
∵EF是AD的垂直平分线,
∴AE=DE,
∴∠EAD=∠EDA,
∵∠EAC=∠EAD﹣∠CAD,∠B=∠ADE﹣∠BAD,
∴∠CAE=∠B,
∴△BAE∽△ACE.
17.证明:∵四边形ABCD是正方形,BP=3PC,Q是CD的中点,
∴QC=QD=AD,CP=AD,
∴,
又∵∠ADQ=∠QCP=90°,
∴△ADQ∽△QCP.
18.解:(1)∵AC=3,CB=5,DB=1,AE=,
∴CD=CB﹣DB=5﹣1=4,
∵EF∥CB,
∴△AEF∽△ACD,
∴,
∴EF===.
(2)∵CE=AC﹣AE=3﹣=,
∴==,
∵=,
∴=,
∵∠C=∠C,
∴△CED∽△CAB,
∴∠EDC=∠B,
∵∠EDC=∠DEF,
∴∠DEF=∠B,
∵∠DFE=∠ADB,
∴△DEF∽△ABD.
19.解:相似.
理由如下:
∵AB==,BC=5,AC==,DE=1,EF==,DF=,
∴=,==,==,
∴==,
∴△ABC∽△DEF.
20.证明:(1)∵GE是AB的垂直平分线,
∴GA=GB,
同理:GD=GC,
在△AGD和△BGC中,
,
∴△AGD≌△BGC(SAS),
∴AD=BC;
(2)∵GA=GB,GD=GC,
∴,
∵∠AGD=∠BGC,
∴∠AGD+∠DGB=∠BGC+∠DGB,
即∠AGB=∠DGC,
∴△AGB∽△DGC,
∴∠GAB=∠GDC,
又∵GE、GF是对应高,
∴,∠AGE=∠DGF,
∴,∠AGD=∠EGF,
∴△AGD∽△EGF.
21.(1)证明:∵在△ABC中,∠BAC=120°,AB=AC,
∴∠B=∠C=30°.
∵∠B+∠BPE+∠BEP=180°,
∴∠BPE+∠BEP=150°,
又∵∠BPE+∠EPF+∠CPF=180°,∠EPF=30°,
∴∠BPE+∠CPF=150°,
∴∠BEP=∠CPF,
∴△BPE∽△CFP(两角对应相等的两个三角形相似).
(2)解:①△BPE∽△CFP;②△BPE与△PFE相似.
下面证明结论:
同(1),可证△BPE∽△CFP,
∴CP:BE=PF:PE,
∵CP=BP,
∴BE:BP=PE:PF.
又∵∠EBP=∠EPF,
∴△BPE∽△PFE(两边对应成比例且夹角相等的两个三角形相似).
22.证明:(1)∵四边形ABCD菱形,
∴AD=CD,∠CDP=∠ADP,CD∥AB,
在△CDP和△ADP中,
,
∴△CDP≌△ADP(SAS),
∴PC=PA,∠DCP=∠DAP,
∵CD∥AB,
∴∠DCP=∠F,
∴∠DAP=∠F,
∵∠APE=∠FPA,
∴△PAE∽△PFA,
∴,
∴PA2=PE PF,
∴PE PF=PC2;
(2)∵CE⊥BC,
∴∠ECB=90°,
∵AD∥BC,
∴∠CEA=∠BCE=90°,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠COP=90°,
∴∠COP=∠CEA,
∵∠OCP=∠ECA,
∴△POC∽△AEC.
一.选择题(共5小题,满分20分)
1.如图,在△ABC中,高BD、CE相交于点F.图中与△AEC一定相似的三角形有( )
A.1个 B.2个 C.3个 D.4个
2.如图,在△ABC中,AB=AC,∠C的平分线交AB于点D,增添下列条件仍然不能判断△ABC∽△CBD的是( )
A.∠A=36° B.BC=DC C.BC2=BD AB D.∠B=∠ACB
3.如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是( )
A. B. C. D.
4.如图,在△ABC中,∠C=45°,将△ABC绕着点B逆时针方向旋转,使点C的对应点C'落在CA的延长线上,得到△A'BC',连接AA',交BC'于点O.下列结论:①∠AC'A'=90°;②AA'=BC';③∠A'BC'=∠A'AC';④△A'OC'∽△BOA.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
5.如图,在正方形网格中有5个格点三角形,分别是:①△ABC,②△ACD,③△ADE,④△AEF,⑤△AGH,其中与⑤相似的三角形是( )
A.①③ B.①④ C.②④ D.①③④
二.填空题(共9小题,满分36分)
6.如图,在△ABC中,∠ACB=90°,CD⊥AB,DE⊥BC,垂足分别为点D,E,则图中与△ABC相似的三角形个数有 个.
7.如图△ABC中,AB=8,AC=6,点D在AC上,AD=2,要在AB上找一E,使△ADE与△ABC相似,AE= .
8.如图,线段AB=9,AC⊥AB于点A,BD⊥AB于点B,AC=2,BD=4,点P为线段AB上一动点,且以A、C、P为顶点的三角形与以B、D、P为顶点的三角形相似,则AP的长为 .
9.如图,正方形ABCD的边长为4,AE=EB,MN=2,线段MN的两端在CB、CD上滑动,当CM= 时,△ADE与△CMN相似.
10.如图,一次函数y=﹣x+6的图象与x轴交于点B,与y轴交于点A,过线段AB的中点P(4,3)作一条直线与△AOB交于点Q,使得所截新三角形与△AOB相似,则点Q坐标是 .
11.如图,点E在线段AB上,CA⊥AB于点A,DB⊥AB于点B,AC=1,AB=5,EB=2,点P是射线BD上的一个动点,则当BP= 时,△CEA与△EPB相似.
12.如图,在矩形ABCD中,AB=10,AD=4,P是CD边上的一个动点,则当△ADP与△BCP相似时,DP= .
13.如图,AB、CD交于点O,且OC=45,OD=30,OB=36,当OA= 时,△AOC与△BOD相似.
14.如图,在矩形ABCD中,E,F分别是CD,BC上的点,∠AEF=90°,有以下结论:①△ADE∽△AEF;②△ECF∽△AEF;③△ADE∽△ECF;④△AEF∽△ABF;⑤△ADE∽△ABF,其中正确的是 (把你认为正确的序号都填上).
三.解答题(共8小题,满分64分)
15.如图,点D为△ABC边AB上一点,AD=2,BD=6,AC=4.求证:△ACD∽△ABC.
16.如图,AD为△ABC的角平分线,AD的垂直平分线交BC的延长线于E,交AB于F,连接AE.求证:△BAE∽△ACE.
17.如图,在边长为4的正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点,求证:△ADQ∽△QCP.
18.如图,在△ABC中,∠C=90°,AC=3,CB=5,D是BC边上一点,且DB=1,点E是AC边上的一个点,且AE=,过点E作EF∥CB交AD于点F.
(1)求EF的长.
(2)求证:△DEF∽△ABD.
19.如图,△ABC与△DEF在5×7的长方形网格中,它们的顶点都在边长为1的小正方形的顶点位置,试判断△ABC与△DEF是否相似,并说明理由.
20.如图,在四边形ABCD中,点E、F分别是AB、CD的中点,过点E作AB的垂线,过点F作CD的垂线,两垂线交于点G,联结AG、BG、CG、DG,且∠AGD=∠BGC.
(1)求证:AD=BC;
(2)求证:△AGD∽△EGF.
21.在△ABC中,AB=AC,∠BAC=120°,P为BC的中点,小明拿着含有30°角的透明直角三角板,使30°角的顶点落在点P上,三角板绕P点旋转.
(1)如图1,当三角板的一直角边和斜边分别与AB、BC交于点E、F时,连接EF,请说明△BPE∽△CFP;
(2)操作:将三角板绕点P旋转到图2情形时,三角板的两边分别交BA的延长线、边AC于点E、F,连接EF.
①探究1:△BPE与△CFP相似吗?请说明理由;
②探究2:△BPE与△PFE相似吗?请说明理由.
22.如图,点P是菱形ABCD的对角线BD上一点,连结CP并延长,交AD于E,交BA的延长线于点F.
(1)求证:PE PF=PC2.
(2)如图2,连接AC交BD于O,连接OE,若CE⊥BC,求证:△POC∽△AEC.
参考答案
一.选择题(共5小题,满分20分)
1.解:∵∠A=∠A,∠AEC=∠ADB=90°,
∴△AEC∽△ADB,
∴∠ACE=∠ABD,
又∵∠AEC=∠BEC=90°,
∴△AEC∽△FEB,
∵∠ACE=∠ACE,∠AEC=∠ADB=90°,
∴△AEC∽△FDC,
故选:C.
2.解:∵AB=AC,
∴∠ABC=∠ACB,
∵CD平分∠ACB,
∴∠ACD=∠BCD,
当∠A=36°时,
∴∠ABC=∠ACB=72°,
∴∠DCB=36°,
∴∠A=∠DCB,
又∵∠DBC=∠ABC,
∴△ABC∽△CBD,故选项A不符合题意;
当BC=DC时,
∴∠CDB=∠CBD,
∴∠ABC=∠ACB=∠CBD=∠CDB,
∴△ABC∽△CBD,故选项B不符合题意;
当BC2=BD AB时,
∴,
又∵∠CBD=∠ABC,
∴△ABC∽△CBD,故选项C不符合题意;
故选:D.
3.解:在△ABC中,∠ACB=135°,AC=,BC=2,
在B、C、D选项中的三角形都没有135°,而在A选项中,三角形的钝角为135°,它的两边分别为1和,
因为=,所以A选项中的三角形与△ABC相似.
故选:A.
4.解:∵将△ABC绕着点B逆时针方向旋转,
∴∠C=∠BC'A'=45°,∠CBC'=∠ABA',BC=BC',AB=BA',
∴∠C=∠BC'C=45°,
∴∠A'C'A=90°=∠CBC'=∠ABC',故①正确;
∴点A,点B,点A',点C'四点共圆,
∴AA'是直径,∠A'BC'=∠A'AC',故②错误,③正确,
∵点A,点B,点A',点C'四点共圆,
∴∠BC'A'=∠BAA',
又∵∠AOB=∠A'OC',
∴△AOB∽△A'OC',故④正确,
故选C.
5.解:由图形知,⑤中∠AHG=135°,
而①②③④中,只有①∠BAC=135°和③∠ADE=135°,
再根据两边成比例可判断,与⑤相似的三角形是①③,
故选:A.
二.填空题(共9小题,满分36分)
6.解:∵CD⊥AB,DE⊥BC,
∴∠CDA=∠CDB=∠DEB=∠DEC=90°=∠ACB,
∴∠A+∠B=90°=∠A+∠ACD=∠B+∠DCB=∠B+∠BDE=∠DCB+∠CDE,
∴∠A=∠BDE=∠BCD,∠B=∠ACD=∠CDE,
∴△ACB∽△ADC∽△DEB∽△CDB∽△CED,
故答案为:4.
7.解:∵∠A是公共角,
∴当,即时,△AED∽△ABC,
解得:AE=;
当,即时,△ADE∽△ABC,
解得:AE=,
故答案为:或
8.解:设AP=x.
∵以A、C、P为顶点的三角形与以B、D、P为顶点的三角形相似,
①当时,,解得x=3.
②当时,,解得x=1或8,
∴当以A、C、P为顶点的三角形与以B、D、P为顶点的三角形相似时,AP的长为1或3或8,
故答案为1或3或8.
9.解:∵AE=EB,
∴AD=2AE,
又∵△AED与以M、N、C为顶点的三角形相似,
∴分两种情况:
①CM与AD是对应边时,CM=2CN,
∴CM2+CN2=MN2=4,
即CM2+CM2=4,
解得:CM=;
②CM与AE是对应边时,CM=CN,
∴CM2+CN2=MN2=4,
即CM2+4CM2=4,
解得:CM=.
综上所述:当CM为或时,△AED与△CMN相似.
故答案是:或.
10.解:∵一次函数y=﹣x+6的图象与x轴交于点B,与y轴交于点A,
∴A(0,6),B(8,0),
∴OA=6,OB=8,AB===10,
如图有两种情形:①当PQ∥OB时,满足条件.
∵AP=PB,
∴AQ=OQ,
∴Q(0,3).
②当PQ′⊥AB时,满足条件.连接AQ′.
∵PA=PB,PQ′⊥AB,
∴Q′A=Q′B,设Q′A=Q′B=m,
在Rt△AOQ′中,则有m2=62+(8﹣m)2,
解得m=,
∴OQ′=8﹣=,
∴Q′(,0).
③当PQ∥y轴时,同法可得P(4,0).
综上所述,满足条件的点Q的坐标为(0,3)或(,0)或(4,0).
11.解:∵CA⊥AB,DB⊥AB,
∴∠A=∠B=90°,
又∵AB=5,EB=2,
∴AE=AB﹣EB=3,
①当△CAE∽△PBE时,=,即=,
解得:PB=;
②当△CAE∽△EBP时,=,即=,
解得:BP=6;
综上,当BP=或6时,△CEA与△EPB相似.
故答案为:或6.
12.解:①当△APD∽△PBC时,
=,即=,
解得:PD=2或PD=8;
②当△PAD∽△PBC时,
=,
即=,
解得:DP=5.
综上所述,DP的长度是2或8或5.
故答案是:2或8或5.
13.解:∵OC=45,OD=30,OB=36,△AOC∽△BOD,
∴,
即,解得OA=54;
若△AOC∽△DOB,
∴,
即,
解得OA=,
综上所述OA的长为54或.
故答案为:54或.
14.解:在矩形ABCD中,
∵∠D=∠C=90°,∠AEF=90°,
∴∠DEA+∠CEF=90°,∠DEA+∠DAE=90°,
∴∠DAE=∠CEF,
∴△ADE∽△ECF,
其余都不符合相似的条件.
故答案为:③.
三.解答题(共8小题,满分64分)
15.解:∵AD=2,BD=6,
∴AB=8,
∴,,
∴,
又∵∠A=∠A,
∴△ACD∽△ABC.
16.证明:∵AD是∠BAC的平分线,
∴∠BAD=∠CAD,
∵EF是AD的垂直平分线,
∴AE=DE,
∴∠EAD=∠EDA,
∵∠EAC=∠EAD﹣∠CAD,∠B=∠ADE﹣∠BAD,
∴∠CAE=∠B,
∴△BAE∽△ACE.
17.证明:∵四边形ABCD是正方形,BP=3PC,Q是CD的中点,
∴QC=QD=AD,CP=AD,
∴,
又∵∠ADQ=∠QCP=90°,
∴△ADQ∽△QCP.
18.解:(1)∵AC=3,CB=5,DB=1,AE=,
∴CD=CB﹣DB=5﹣1=4,
∵EF∥CB,
∴△AEF∽△ACD,
∴,
∴EF===.
(2)∵CE=AC﹣AE=3﹣=,
∴==,
∵=,
∴=,
∵∠C=∠C,
∴△CED∽△CAB,
∴∠EDC=∠B,
∵∠EDC=∠DEF,
∴∠DEF=∠B,
∵∠DFE=∠ADB,
∴△DEF∽△ABD.
19.解:相似.
理由如下:
∵AB==,BC=5,AC==,DE=1,EF==,DF=,
∴=,==,==,
∴==,
∴△ABC∽△DEF.
20.证明:(1)∵GE是AB的垂直平分线,
∴GA=GB,
同理:GD=GC,
在△AGD和△BGC中,
,
∴△AGD≌△BGC(SAS),
∴AD=BC;
(2)∵GA=GB,GD=GC,
∴,
∵∠AGD=∠BGC,
∴∠AGD+∠DGB=∠BGC+∠DGB,
即∠AGB=∠DGC,
∴△AGB∽△DGC,
∴∠GAB=∠GDC,
又∵GE、GF是对应高,
∴,∠AGE=∠DGF,
∴,∠AGD=∠EGF,
∴△AGD∽△EGF.
21.(1)证明:∵在△ABC中,∠BAC=120°,AB=AC,
∴∠B=∠C=30°.
∵∠B+∠BPE+∠BEP=180°,
∴∠BPE+∠BEP=150°,
又∵∠BPE+∠EPF+∠CPF=180°,∠EPF=30°,
∴∠BPE+∠CPF=150°,
∴∠BEP=∠CPF,
∴△BPE∽△CFP(两角对应相等的两个三角形相似).
(2)解:①△BPE∽△CFP;②△BPE与△PFE相似.
下面证明结论:
同(1),可证△BPE∽△CFP,
∴CP:BE=PF:PE,
∵CP=BP,
∴BE:BP=PE:PF.
又∵∠EBP=∠EPF,
∴△BPE∽△PFE(两边对应成比例且夹角相等的两个三角形相似).
22.证明:(1)∵四边形ABCD菱形,
∴AD=CD,∠CDP=∠ADP,CD∥AB,
在△CDP和△ADP中,
,
∴△CDP≌△ADP(SAS),
∴PC=PA,∠DCP=∠DAP,
∵CD∥AB,
∴∠DCP=∠F,
∴∠DAP=∠F,
∵∠APE=∠FPA,
∴△PAE∽△PFA,
∴,
∴PA2=PE PF,
∴PE PF=PC2;
(2)∵CE⊥BC,
∴∠ECB=90°,
∵AD∥BC,
∴∠CEA=∠BCE=90°,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠COP=90°,
∴∠COP=∠CEA,
∵∠OCP=∠ECA,
∴△POC∽△AEC.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
