2022-2023学年人教版八年级数学上册12.3 角的平分线的性质 同步练习 (Word版含答案)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册12.3 角的平分线的性质 同步练习 (Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 582.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-27 08:23:20 | ||
图片预览


文档简介
第十二章 全等三角形
12.3 角的平分线的性质(同步练习)
一、单选题
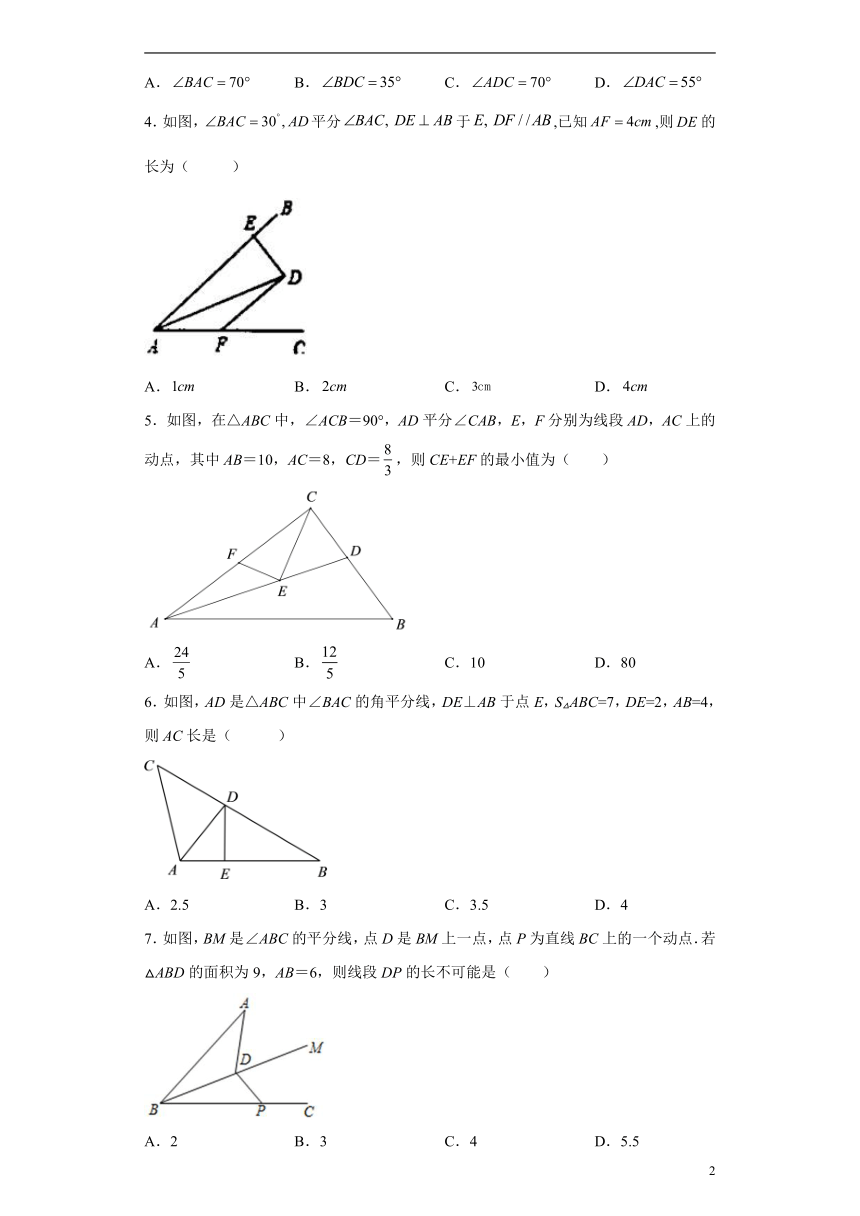
1.如图,已知在中,,,嘉淇通过尺规作图得到,交于点D,根据其作图痕迹,可得的度数为( )
A.120° B.110° C.100° D.98°
2.如图,点O是△ABC中∠BCA,∠ABC的平分线的交点,已知△ABC的面积是12,周长是8,则点O到边BC的距离是( )
A.1 B.2
C.3 D.4
3.如图,在中,,点在的延长线上,的平分线与的平分线相交于点,连接,下列结论中不正确的是( )
A. B. C. D.
4.如图,平分于,已知,则的长为( )
A. B. C. D.
5.如图,在△ABC中,∠ACB=90°,AD平分∠CAB,E,F分别为线段AD,AC上的动点,其中AB=10,AC=8,CD=,则CE+EF的最小值为( )
A. B. C.10 D.80
6.如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC长是( )
A.2.5 B.3 C.3.5 D.4
7.如图,BM是∠ABC的平分线,点D是BM上一点,点P为直线BC上的一个动点.若△ABD的面积为9,AB=6,则线段DP的长不可能是( )
A.2 B.3 C.4 D.5.5
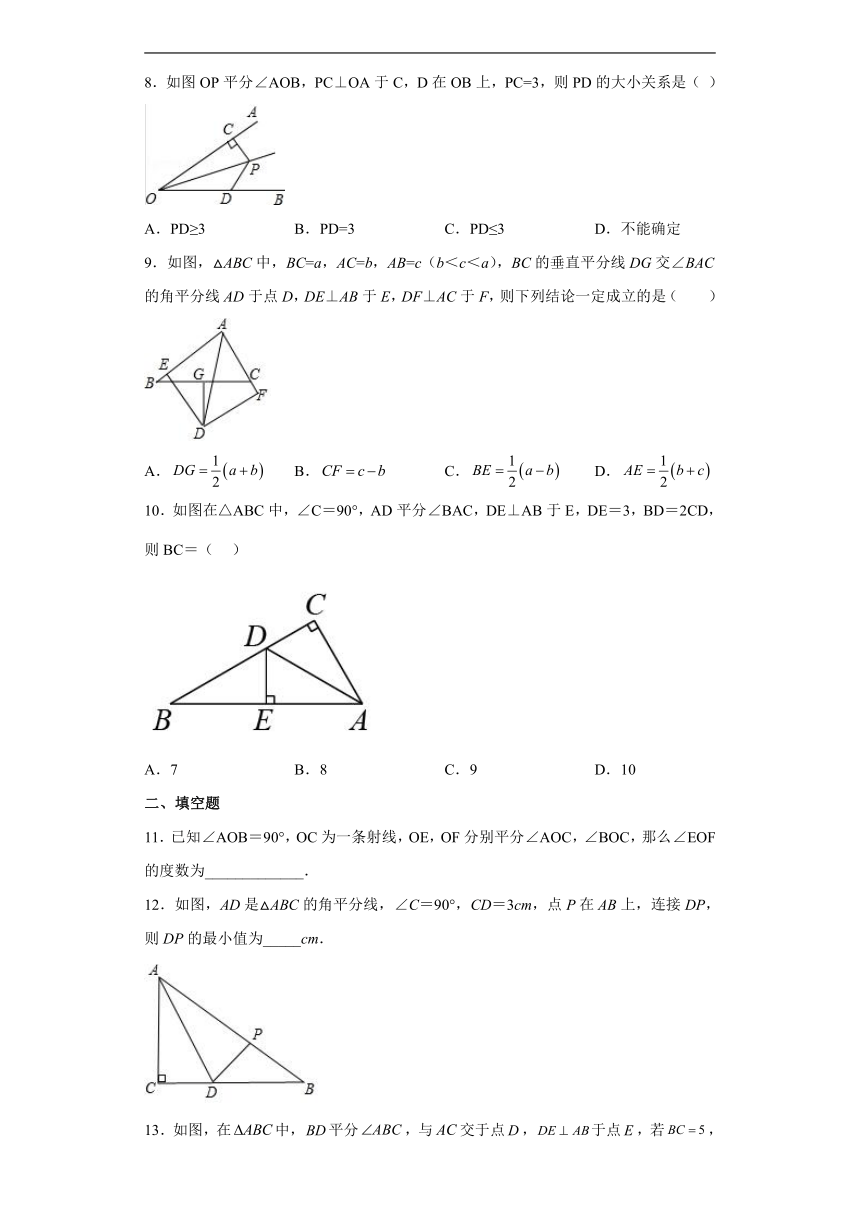
8.如图OP平分∠AOB,PC⊥OA于C,D在OB上,PC=3,则PD的大小关系是( )
A.PD≥3 B.PD=3 C.PD≤3 D.不能确定
9.如图,△ABC中,BC=a,AC=b,AB=c(b<c<a),BC的垂直平分线DG交∠BAC的角平分线AD于点D,DE⊥AB于E,DF⊥AC于F,则下列结论一定成立的是( )
A. B. C. D.
10.如图在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,DE=3,BD=2CD,则BC=( )
A.7 B.8 C.9 D.10
二、填空题
11.已知∠AOB=90°,OC为一条射线,OE,OF分别平分∠AOC,∠BOC,那么∠EOF 的度数为_____________.
12.如图,AD是△ABC的角平分线,∠C=90°,CD=3cm,点P在AB上,连接DP,则DP的最小值为_____cm.
13.如图,在中,平分,与交于点,于点,若,的面积为5,则的长为______________.
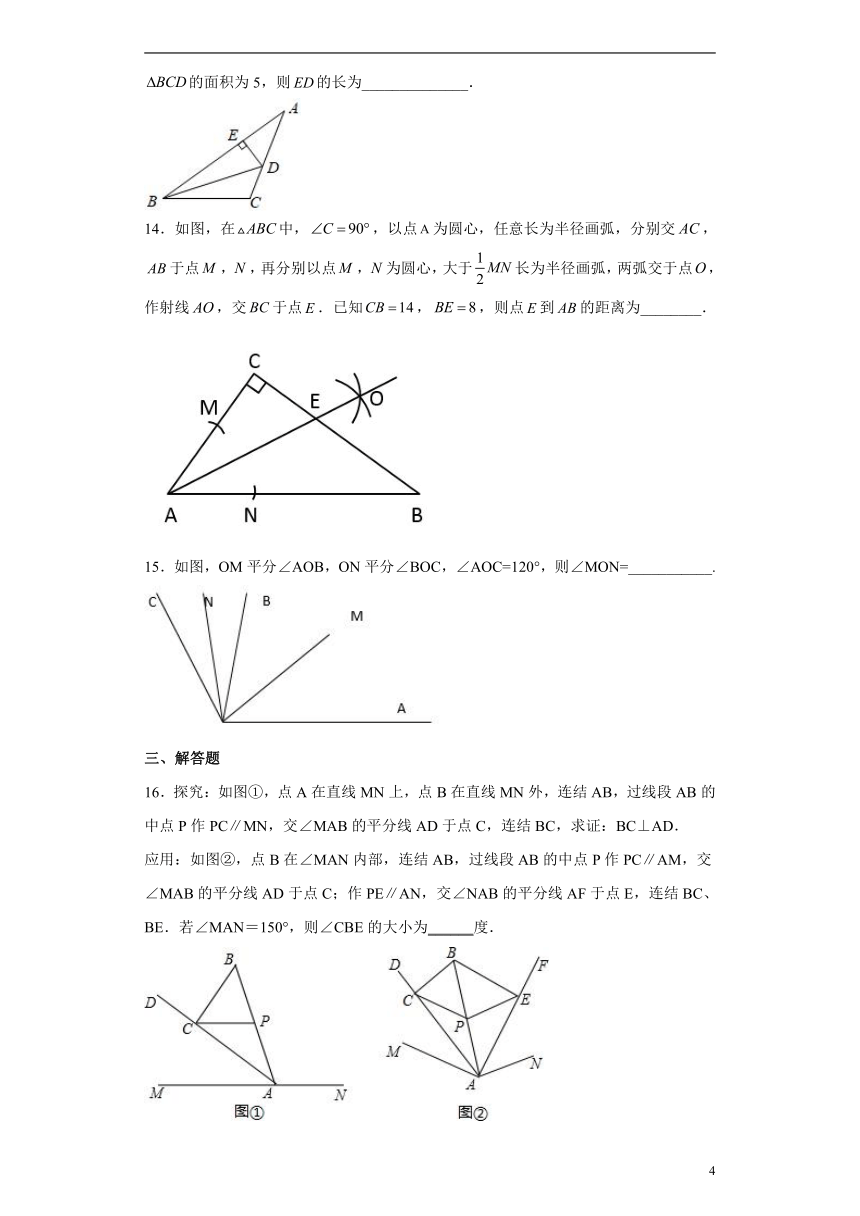
14.如图,在中,,以点为圆心,任意长为半径画弧,分别交,于点,,再分别以点,为圆心,大于长为半径画弧,两弧交于点,作射线,交于点.已知,,则点到的距离为________.
15.如图,OM平分∠AOB,ON平分∠BOC,∠AOC=120°,则∠MON=___________.
三、解答题
16.探究:如图①,点A在直线MN上,点B在直线MN外,连结AB,过线段AB的中点P作PC∥MN,交∠MAB的平分线AD于点C,连结BC,求证:BC⊥AD.
应用:如图②,点B在∠MAN内部,连结AB,过线段AB的中点P作PC∥AM,交∠MAB的平分线AD于点C;作PE∥AN,交∠NAB的平分线AF于点E,连结BC、BE.若∠MAN=150°,则∠CBE的大小为______度.
17.如图,已知在四边形ABCD中,AD∥BC,连接AC、BD.
(1)用基本尺规作图:作∠ACB的角平分线CM,交DA的延长线于点E,交BD于F(保留画图的痕迹,不写作法);
(2)若F是BD的中点,AD=4,AC=3,求BC的长.
18.如图,直线表示三条相互交叉的公路,现在要建设一个货物中转站,要求它到三条公路的距离相等,请确定中转站p的位置.
要求:尺规作图,保留痕迹,标注字母,不写作法.
19.已知:如图,P 是 OC 上一点,PD⊥OA 于 D,PE⊥OB 于 E,F、G分别是 OA、OB 上的点,且 PF=PG,DF=EG. 求证:OC 是∠AOB 的平分线.
20.四边形ABCD中,∠ABC+∠D=180°,AC平分∠BAD,CE⊥AB于E,CF⊥AD于F.
(1)求证:△CBE≌△CDF;
(2)若AB=3,DF=2,求AF的长.
参考答案:
1.B
【详解】
根据作图痕迹可知,是∠ABC的平分线,
∵,,
∴
∵是∠ABC的平分线,
∴
∴
故选:B.
2.C
【详解】
如图,过点O作OE⊥AB于E,OF⊥AC于F,连接OA.
∵点O是∠ABC,∠ACB平分线的交点,
∴OE=OD,OF=OD,即OE=OF=OD
∴S△ABC=S△ABO+S△BCO+S△ACO=AB·OE+BC·OD+AC·OF=×OD×(AB+BC+AC)=×OD×8=12
OD=3
故选:C
3.C
【详解】
解:选项:在中,,
,故选项不符合题意;
选项:,
,
平分,平分,
,
故选项不符合题意;
选项:在中,
故选项符合题意;
选项:分别是和的平分线
到的距离相等,
是的外角平分线,
,
故选项不符合题意.
故选.
4.B
【详解】
作DG⊥AC于G,
∵AD平分∠BAC,
∴∠BAD=∠CAD,DE=DG,
∵DF∥AB,
∴∠ADF=∠BAD,∠DFC=∠BAC=30°,
∴∠ADF=∠CAD,
∴DF=AF=4m,
∴Rt△FDG中,DG=DF=2cm,
∴DE=2cm.
故选:B.
5.A
【详解】
如图,过点作,交于,过点作于点,过点作于点,作关于的对称点,连接,
AD平分∠CAB,
,
E,F分别为线段AD,AC上的动点,
当分别与点重合时,取得最小值,最小值为的长
又
的最小值为
故选A
6.B
【详解】
解:作DH⊥AC于H,如图,
∵AD是△ABC中∠BAC的角平分线,DE⊥AB,DH⊥AC,
∴DH=DE=2,
∵S△ABC=S△ADC+S△ABD,
∴×2×AC+×2×4=7,
∴AC=3.
故选:B.
7.A
【详解】
过点D作DE⊥AB于E,DF⊥BC于F,
∵△ABD的面积为9,AB=6,
∴DE==3,
∵BM是∠ABC的平分线,
∴DE=3,
∴DP≥3,
故选A.
8.A
【详解】
试题分析:过点P作PE⊥OB于E,根据角平分线上的点到角的两边距离相等可得PE=PC,再根据垂线段最短解答.
解:如图,过点P作PE⊥OB于E,
∵OP平分∠AOB,PC⊥OA,
∴PE=PC=3,
∵D在OB上,
∴PD≥PE,
∴PD≥3.
故选A.
考点:角平分线的性质;垂线段最短.
9.D
【详解】
如图,连接DB、DC.
∵AD平分∠BAC,DE⊥AB,DF⊥AC,∴DE=DF,∠DEB=∠DFC=90°.
∵DG垂直平分线段BC,∴DB=DC.
在Rt△DEB和Rt△DFC中,∵,∴△DEB≌△DFC,∴BE=CF,同理△ADE≌△ADF,∴AE=AF,∴AB+AC=(AE+BE)+(AF﹣CF)=2AE,∴AE=(AB+AC)=(b+c).
故选D.
10.C
【详解】
解:∵在△ADE和△ADC中,
∴△ADE≌△ADC,
∴CD=DE,
∵BD=2CD,
∴BC=BD+CD=3DE=9.
故答案为9.
故选C
11.45°或135°
【详解】
解:①OC在∠AOB内部,
如图所示:
∵OE,OF分别平分∠AOC和∠BOC,∴∠COE=∠AOC,∠COF=∠BOC,
∴∠COE+∠COF=∠AOC+∠BOC,
即∠EOF=∠AOB,
又∵∠AOB=90°,
∴∠EOF=45°;
②如图,
当OC在∠AOB外部时,
∵OE,OF分别平分∠AOC和∠BOC,
∴∠AOE=∠EOC=∠AOC,∠BOF=∠FOC=∠BOC,
∴∠EOF=∠EOC+∠FOC=(360° 90°)÷2,
∴∠EOF=135°,
综上所述:∠EOF=45°或135°.
故答案为45°或135°.
12.3.
【详解】
作DP′⊥AB于P′,
∵AD是△ABC的角平分线,∠C=90°,DP′⊥AB
∴DP′=DC=3cm,
则DP的最小值为3cm,
故答案为3.
13.2
【详解】
过点作于,如图,
的面积为5,
,
而,
,
平分,,,
.
故答案为2.
14.6
【详解】
解:如图,过点E作ET⊥AB于T.
∵BC=14,BE=8,
∴EC=BCBE=6,
由作图可知,AE平分⊥CAB,
∵EC⊥AC,ET⊥AB,
∴ET=EC=6,
故答案为:6.
15.60°
【详解】
∵OM平分∠AOB,ON平分∠BOC,
∴∠AOM=∠BOM=∠AOB,∠BON=∠CON=∠BOC,
∴∠BOM+∠BON=∠AOB+∠BOC=∠AOC=×120°=60°,
即∠MON=60°.
故答案为60°.
16.探究:证明见解析;应用:150.
【详解】
解:探究:∵PC∥MN,
∴∠PCA=∠MAC.
∵AD为∠MAB的平分线,
∴∠MAC=∠PAC.
∴∠PCA=∠PAC,
∴PC=PA.
∵PA=PB,
∴PC=PB,
∴∠B=∠BCP.
∵∠B+∠BCP+∠PCA+∠PAC=180°,
∴∠BCA=90°,
∴BC⊥AD;
应用:∵∠MAB的平分线AD,∠NAB的平分线AF,∠MAN=150°,
∴∠BAC+∠BAE=75°,
由探究得:∠BAC+∠BAE+∠CBA+∠ABE=180°,
∴∠CBE=∠CBA+∠ABE=180°﹣75°=105°
故答案为:105.
17.(1)见解答;(2)7
【详解】
解:(1)如图,CM为所作;
以C为圆心,以任意长为半径画弧,分别交AC,BC与G、N两点,分别以G、N为圆心,以大于GN的一半长为半径画弧,交于点H,连接CH并延长交DA的延长线于E.
(2)∵CM平分∠ACB,
∴∠BCE=∠ACE,
∵AD∥BC,
∴∠AEC=∠BCE,
∴∠ACE=∠AEC,
∴AE=AC=3,
∵F是BD的中点,
∴BF=AF,
在△BCF和△DEF中,
,
∴△BCF≌△DEF(AAS),
∴BC=DE=4+3=7.
18.作图见解析部分.到三条公路的距离相等的点有四个.
【详解】
解:如图,满足条件的点P有四个,如图所示:
19.见解析
【详解】
证明:在 Rt△PFD 和 Rt△PGE 中, ,
∴Rt△PFD≌Rt△PGE(HL),
∴PD=PE,
∵P 是 OC 上一点,PD⊥OA,PE⊥OB,
∴OC 是∠AOB 的平分线.
20.(1)详见解析;(2)5.
【详解】
(1)证明:∵AC平分∠BAD,CE⊥AB,CF⊥AD
∴CE=CF
∵∠ABC+∠D=180°,∠ABC+∠EBC=180°
∴∠EBC=∠D.
在△CBE与△CDF中,
,
∴△CBE≌△CDF(AAS);
(2)在Rt△ACE与Rt△ACF中,
,
∴Rt△ACE≌Rt△ACF(HL),
∴AE=AF,
∴AB+DF=AB+BE=AE=AF,
∵AB=3,DF=2,
∴AF=3+2=5.
12.3 角的平分线的性质(同步练习)
一、单选题
1.如图,已知在中,,,嘉淇通过尺规作图得到,交于点D,根据其作图痕迹,可得的度数为( )
A.120° B.110° C.100° D.98°
2.如图,点O是△ABC中∠BCA,∠ABC的平分线的交点,已知△ABC的面积是12,周长是8,则点O到边BC的距离是( )
A.1 B.2
C.3 D.4
3.如图,在中,,点在的延长线上,的平分线与的平分线相交于点,连接,下列结论中不正确的是( )
A. B. C. D.
4.如图,平分于,已知,则的长为( )
A. B. C. D.
5.如图,在△ABC中,∠ACB=90°,AD平分∠CAB,E,F分别为线段AD,AC上的动点,其中AB=10,AC=8,CD=,则CE+EF的最小值为( )
A. B. C.10 D.80
6.如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC长是( )
A.2.5 B.3 C.3.5 D.4
7.如图,BM是∠ABC的平分线,点D是BM上一点,点P为直线BC上的一个动点.若△ABD的面积为9,AB=6,则线段DP的长不可能是( )
A.2 B.3 C.4 D.5.5
8.如图OP平分∠AOB,PC⊥OA于C,D在OB上,PC=3,则PD的大小关系是( )
A.PD≥3 B.PD=3 C.PD≤3 D.不能确定
9.如图,△ABC中,BC=a,AC=b,AB=c(b<c<a),BC的垂直平分线DG交∠BAC的角平分线AD于点D,DE⊥AB于E,DF⊥AC于F,则下列结论一定成立的是( )
A. B. C. D.
10.如图在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,DE=3,BD=2CD,则BC=( )
A.7 B.8 C.9 D.10
二、填空题
11.已知∠AOB=90°,OC为一条射线,OE,OF分别平分∠AOC,∠BOC,那么∠EOF 的度数为_____________.
12.如图,AD是△ABC的角平分线,∠C=90°,CD=3cm,点P在AB上,连接DP,则DP的最小值为_____cm.
13.如图,在中,平分,与交于点,于点,若,的面积为5,则的长为______________.
14.如图,在中,,以点为圆心,任意长为半径画弧,分别交,于点,,再分别以点,为圆心,大于长为半径画弧,两弧交于点,作射线,交于点.已知,,则点到的距离为________.
15.如图,OM平分∠AOB,ON平分∠BOC,∠AOC=120°,则∠MON=___________.
三、解答题
16.探究:如图①,点A在直线MN上,点B在直线MN外,连结AB,过线段AB的中点P作PC∥MN,交∠MAB的平分线AD于点C,连结BC,求证:BC⊥AD.
应用:如图②,点B在∠MAN内部,连结AB,过线段AB的中点P作PC∥AM,交∠MAB的平分线AD于点C;作PE∥AN,交∠NAB的平分线AF于点E,连结BC、BE.若∠MAN=150°,则∠CBE的大小为______度.
17.如图,已知在四边形ABCD中,AD∥BC,连接AC、BD.
(1)用基本尺规作图:作∠ACB的角平分线CM,交DA的延长线于点E,交BD于F(保留画图的痕迹,不写作法);
(2)若F是BD的中点,AD=4,AC=3,求BC的长.
18.如图,直线表示三条相互交叉的公路,现在要建设一个货物中转站,要求它到三条公路的距离相等,请确定中转站p的位置.
要求:尺规作图,保留痕迹,标注字母,不写作法.
19.已知:如图,P 是 OC 上一点,PD⊥OA 于 D,PE⊥OB 于 E,F、G分别是 OA、OB 上的点,且 PF=PG,DF=EG. 求证:OC 是∠AOB 的平分线.
20.四边形ABCD中,∠ABC+∠D=180°,AC平分∠BAD,CE⊥AB于E,CF⊥AD于F.
(1)求证:△CBE≌△CDF;
(2)若AB=3,DF=2,求AF的长.
参考答案:
1.B
【详解】
根据作图痕迹可知,是∠ABC的平分线,
∵,,
∴
∵是∠ABC的平分线,
∴
∴
故选:B.
2.C
【详解】
如图,过点O作OE⊥AB于E,OF⊥AC于F,连接OA.
∵点O是∠ABC,∠ACB平分线的交点,
∴OE=OD,OF=OD,即OE=OF=OD
∴S△ABC=S△ABO+S△BCO+S△ACO=AB·OE+BC·OD+AC·OF=×OD×(AB+BC+AC)=×OD×8=12
OD=3
故选:C
3.C
【详解】
解:选项:在中,,
,故选项不符合题意;
选项:,
,
平分,平分,
,
故选项不符合题意;
选项:在中,
故选项符合题意;
选项:分别是和的平分线
到的距离相等,
是的外角平分线,
,
故选项不符合题意.
故选.
4.B
【详解】
作DG⊥AC于G,
∵AD平分∠BAC,
∴∠BAD=∠CAD,DE=DG,
∵DF∥AB,
∴∠ADF=∠BAD,∠DFC=∠BAC=30°,
∴∠ADF=∠CAD,
∴DF=AF=4m,
∴Rt△FDG中,DG=DF=2cm,
∴DE=2cm.
故选:B.
5.A
【详解】
如图,过点作,交于,过点作于点,过点作于点,作关于的对称点,连接,
AD平分∠CAB,
,
E,F分别为线段AD,AC上的动点,
当分别与点重合时,取得最小值,最小值为的长
又
的最小值为
故选A
6.B
【详解】
解:作DH⊥AC于H,如图,
∵AD是△ABC中∠BAC的角平分线,DE⊥AB,DH⊥AC,
∴DH=DE=2,
∵S△ABC=S△ADC+S△ABD,
∴×2×AC+×2×4=7,
∴AC=3.
故选:B.
7.A
【详解】
过点D作DE⊥AB于E,DF⊥BC于F,
∵△ABD的面积为9,AB=6,
∴DE==3,
∵BM是∠ABC的平分线,
∴DE=3,
∴DP≥3,
故选A.
8.A
【详解】
试题分析:过点P作PE⊥OB于E,根据角平分线上的点到角的两边距离相等可得PE=PC,再根据垂线段最短解答.
解:如图,过点P作PE⊥OB于E,
∵OP平分∠AOB,PC⊥OA,
∴PE=PC=3,
∵D在OB上,
∴PD≥PE,
∴PD≥3.
故选A.
考点:角平分线的性质;垂线段最短.
9.D
【详解】
如图,连接DB、DC.
∵AD平分∠BAC,DE⊥AB,DF⊥AC,∴DE=DF,∠DEB=∠DFC=90°.
∵DG垂直平分线段BC,∴DB=DC.
在Rt△DEB和Rt△DFC中,∵,∴△DEB≌△DFC,∴BE=CF,同理△ADE≌△ADF,∴AE=AF,∴AB+AC=(AE+BE)+(AF﹣CF)=2AE,∴AE=(AB+AC)=(b+c).
故选D.
10.C
【详解】
解:∵在△ADE和△ADC中,
∴△ADE≌△ADC,
∴CD=DE,
∵BD=2CD,
∴BC=BD+CD=3DE=9.
故答案为9.
故选C
11.45°或135°
【详解】
解:①OC在∠AOB内部,
如图所示:
∵OE,OF分别平分∠AOC和∠BOC,∴∠COE=∠AOC,∠COF=∠BOC,
∴∠COE+∠COF=∠AOC+∠BOC,
即∠EOF=∠AOB,
又∵∠AOB=90°,
∴∠EOF=45°;
②如图,
当OC在∠AOB外部时,
∵OE,OF分别平分∠AOC和∠BOC,
∴∠AOE=∠EOC=∠AOC,∠BOF=∠FOC=∠BOC,
∴∠EOF=∠EOC+∠FOC=(360° 90°)÷2,
∴∠EOF=135°,
综上所述:∠EOF=45°或135°.
故答案为45°或135°.
12.3.
【详解】
作DP′⊥AB于P′,
∵AD是△ABC的角平分线,∠C=90°,DP′⊥AB
∴DP′=DC=3cm,
则DP的最小值为3cm,
故答案为3.
13.2
【详解】
过点作于,如图,
的面积为5,
,
而,
,
平分,,,
.
故答案为2.
14.6
【详解】
解:如图,过点E作ET⊥AB于T.
∵BC=14,BE=8,
∴EC=BCBE=6,
由作图可知,AE平分⊥CAB,
∵EC⊥AC,ET⊥AB,
∴ET=EC=6,
故答案为:6.
15.60°
【详解】
∵OM平分∠AOB,ON平分∠BOC,
∴∠AOM=∠BOM=∠AOB,∠BON=∠CON=∠BOC,
∴∠BOM+∠BON=∠AOB+∠BOC=∠AOC=×120°=60°,
即∠MON=60°.
故答案为60°.
16.探究:证明见解析;应用:150.
【详解】
解:探究:∵PC∥MN,
∴∠PCA=∠MAC.
∵AD为∠MAB的平分线,
∴∠MAC=∠PAC.
∴∠PCA=∠PAC,
∴PC=PA.
∵PA=PB,
∴PC=PB,
∴∠B=∠BCP.
∵∠B+∠BCP+∠PCA+∠PAC=180°,
∴∠BCA=90°,
∴BC⊥AD;
应用:∵∠MAB的平分线AD,∠NAB的平分线AF,∠MAN=150°,
∴∠BAC+∠BAE=75°,
由探究得:∠BAC+∠BAE+∠CBA+∠ABE=180°,
∴∠CBE=∠CBA+∠ABE=180°﹣75°=105°
故答案为:105.
17.(1)见解答;(2)7
【详解】
解:(1)如图,CM为所作;
以C为圆心,以任意长为半径画弧,分别交AC,BC与G、N两点,分别以G、N为圆心,以大于GN的一半长为半径画弧,交于点H,连接CH并延长交DA的延长线于E.
(2)∵CM平分∠ACB,
∴∠BCE=∠ACE,
∵AD∥BC,
∴∠AEC=∠BCE,
∴∠ACE=∠AEC,
∴AE=AC=3,
∵F是BD的中点,
∴BF=AF,
在△BCF和△DEF中,
,
∴△BCF≌△DEF(AAS),
∴BC=DE=4+3=7.
18.作图见解析部分.到三条公路的距离相等的点有四个.
【详解】
解:如图,满足条件的点P有四个,如图所示:
19.见解析
【详解】
证明:在 Rt△PFD 和 Rt△PGE 中, ,
∴Rt△PFD≌Rt△PGE(HL),
∴PD=PE,
∵P 是 OC 上一点,PD⊥OA,PE⊥OB,
∴OC 是∠AOB 的平分线.
20.(1)详见解析;(2)5.
【详解】
(1)证明:∵AC平分∠BAD,CE⊥AB,CF⊥AD
∴CE=CF
∵∠ABC+∠D=180°,∠ABC+∠EBC=180°
∴∠EBC=∠D.
在△CBE与△CDF中,
,
∴△CBE≌△CDF(AAS);
(2)在Rt△ACE与Rt△ACF中,
,
∴Rt△ACE≌Rt△ACF(HL),
∴AE=AF,
∴AB+DF=AB+BE=AE=AF,
∵AB=3,DF=2,
∴AF=3+2=5.
