2022-2023学年人教版八年级数学上册12.2 三角形全等的判定 同步练习 (Word版含答案)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册12.2 三角形全等的判定 同步练习 (Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 291.4KB | ||
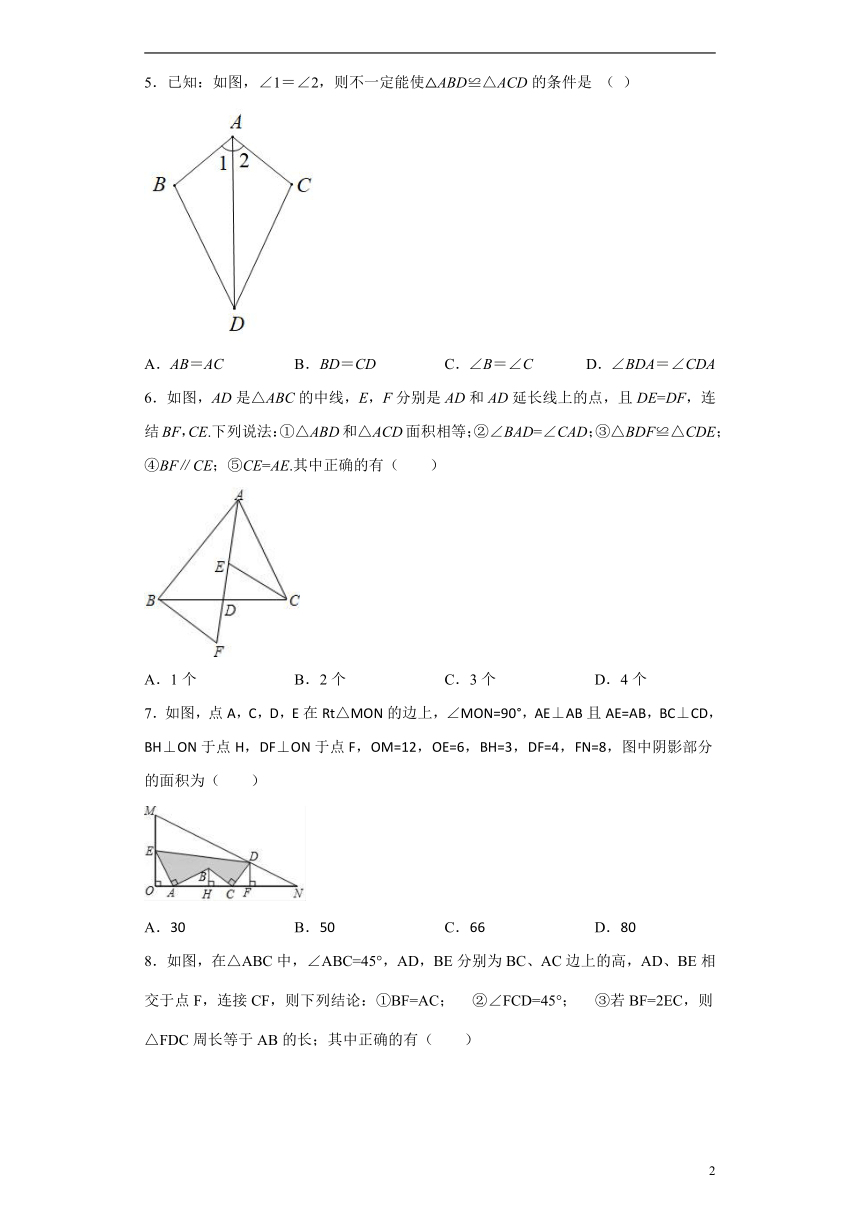
| 资源类型 | 教案 | ||
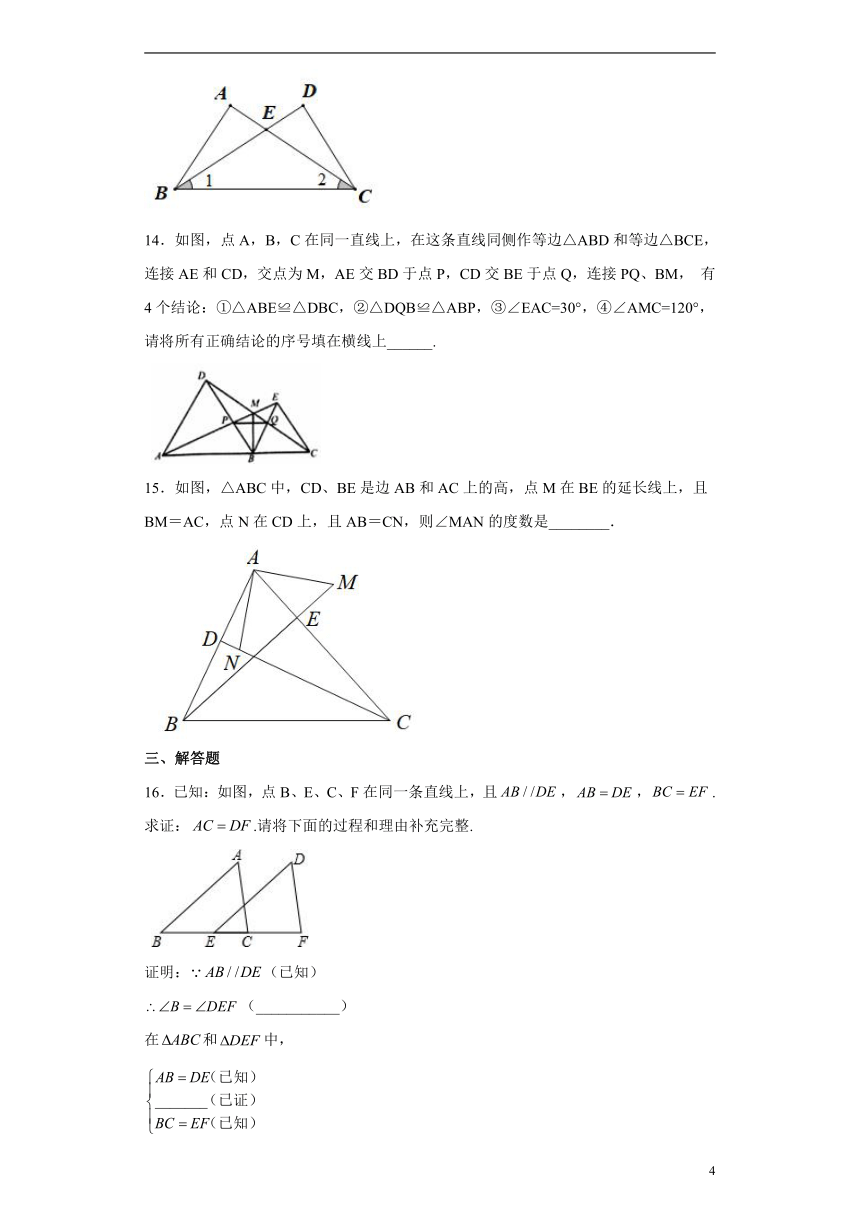
| 版本资源 | 人教版 | ||
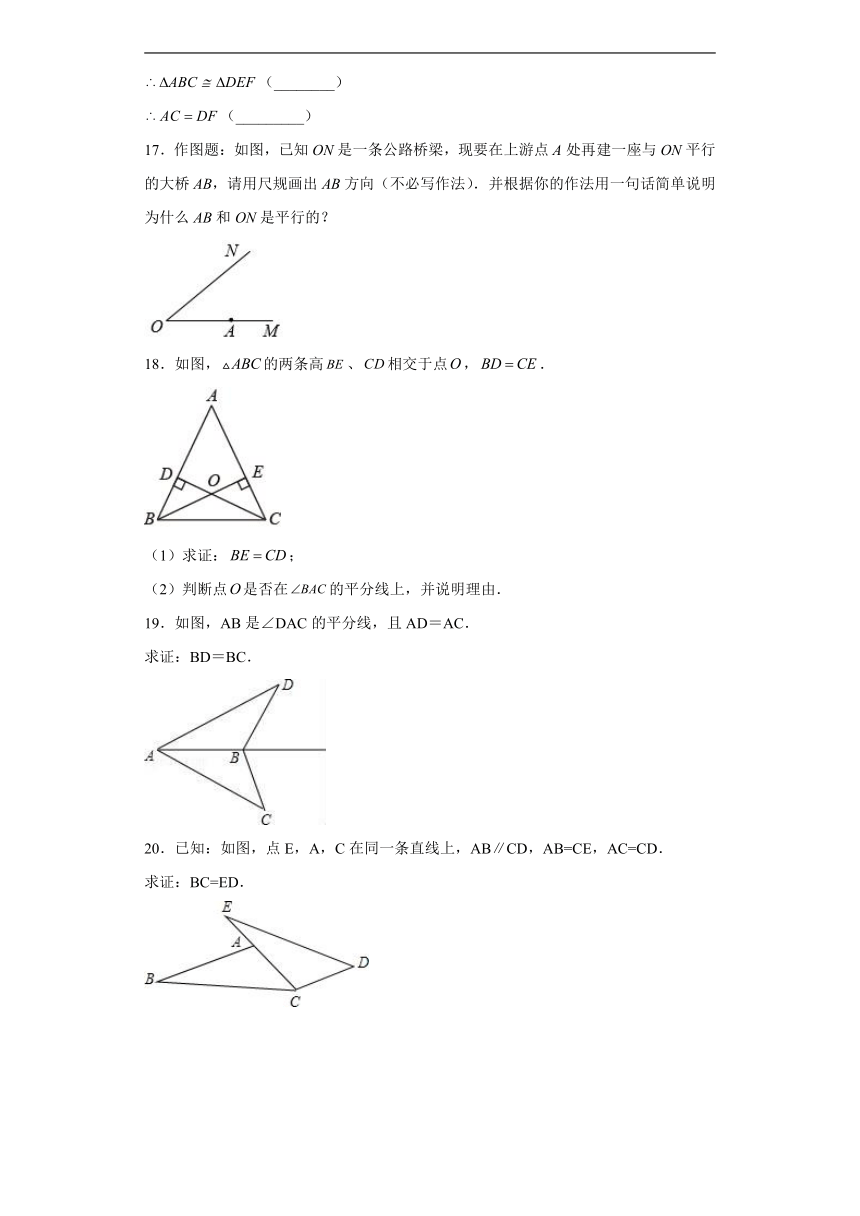
| 科目 | 数学 | ||
| 更新时间 | 2022-08-27 08:26:57 | ||
图片预览


文档简介
第十二章 全等三角形
12.2 三角形全等的判定(同步练习)
一、单选题
1.下列说法错误的是( )
A.三边分别相等的两个三角形全等
B.三角分别相等的两个三角形全等
C.两边和它们的夹角分别相等的两个三角形全等
D.斜边和一条直角边分别相等的两个直角三角形全等
2.下列条件中,不能判定△ABC≌△A′B′C′,的是( )
A.∠A=∠A,∠C=∠C,AC=A′C′
B.∠B=∠B′,BC=B′C′,AB=A′B′
C.∠A=∠A′=80°,∠B=60°,∠C′=40°,AB=A′B′
D.∠A=∠A′,BC=B′C′,AB=A′B′
3.如图,在中,于点,于点,,交于点,≌.若,,则的面积为( ).
A.24 B.18 C.12 D.8
4.如图,在△ABC 中,AB=8,AC=5,AD是△ABC的中线,则AD的取值范围是( )
A.35.已知:如图,∠1=∠2,则不一定能使△ABD≌△ACD的条件是 ( )
A.AB=AC B.BD=CD C.∠B=∠C D.∠BDA=∠CDA
6.如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连结BF,CE.下列说法:①△ABD和△ACD面积相等;②∠BAD=∠CAD;③△BDF≌△CDE;④BF∥CE;⑤CE=AE.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
7.如图,点A,C,D,E在Rt△MON的边上,∠MON=90°,AE⊥AB且AE=AB,BC⊥CD,BH⊥ON于点H,DF⊥ON于点F,OM=12,OE=6,BH=3,DF=4,FN=8,图中阴影部分的面积为( )
A.30 B.50 C.66 D.80
8.如图,在△ABC中,∠ABC=45°,AD,BE分别为BC、AC边上的高,AD、BE相交于点F,连接CF,则下列结论:①BF=AC; ②∠FCD=45°; ③若BF=2EC,则△FDC周长等于AB的长;其中正确的有( )
A.0个 B.1个 C.2个 D.3个
9.如图,AB=DC,BF=CE,需补充一个条件,就能使△ABE≌△DCF,小明给出以下四个答案:①AE=DF;②AE∥DF;③AB∥DC;④∠A=∠D,其中正确的是( )
A.①②③④ B.①②③ C.①② D.①③
10.下列命题是真命题的是( )
A.两边及一个角对应相等的两个三角形全等
B.两角及一边对应相等的两个三角形全等
C.三个角对应相等的两个三角形全等
D.面积相等的两个三角形全等
二、填空题
11.如图,已知AE平分∠BAC,点D是AE上一点,连接BD,CD.请你添加一个适当的条件,使△ABD≌△ACD.添加的条件是:____.(写出一个即可)
12.如图所示,已知AC与BD相交于点E,,,,,则CE的长为______
13.如图交于点E,下列①②③④正确的有________
14.如图,点A,B,C在同一直线上,在这条直线同侧作等边△ABD和等边△BCE,连接AE和CD,交点为M,AE交BD于点P,CD交BE于点Q,连接PQ、BM, 有4个结论:①△ABE≌△DBC,②△DQB≌△ABP,③∠EAC=30°,④∠AMC=120°,请将所有正确结论的序号填在横线上______.
15.如图,△ABC中,CD、BE是边AB和AC上的高,点M在BE的延长线上,且BM=AC,点N在CD上,且AB=CN,则∠MAN的度数是________.
三、解答题
16.已知:如图,点B、E、C、F在同一条直线上,且,,.求证:.请将下面的过程和理由补充完整.
证明:(已知)
(___________)
在和中,
(________)
(_________)
17.作图题:如图,已知ON是一条公路桥梁,现要在上游点A处再建一座与ON平行的大桥AB,请用尺规画出AB方向(不必写作法).并根据你的作法用一句话简单说明为什么AB和ON是平行的?
18.如图,的两条高、相交于点,.
(1)求证:;
(2)判断点是否在的平分线上,并说明理由.
19.如图,AB是∠DAC的平分线,且AD=AC.
求证:BD=BC.
20.已知:如图,点E,A,C在同一条直线上,AB∥CD,AB=CE,AC=CD.
求证:BC=ED.
参考答案:
1.B
【详解】
解:A、三边分别相等的两个三角形全等,此项说法正确;
B、三角分别相等的两个三角形全等,此项说法错误;
C、两边和它们的夹角分别相等的两个三角形全等,此项说法正确;
D、斜边和一条直角边分别相等的两个直角三角形全等,此项说法正确;
故选:B.
2.D
【详解】
试题分析:根据三角形全等的判定方法,SSS、SAS、ASA、AAS,逐一检验.
考点:全等三角形的判定
3.C
【详解】
∵,
∴AD=BD=4,
∵BC=BD+CD=4+2=6,
∴
故选C.
4.B
【详解】
解:延长AD到E,使AD=DE,连结BE.
∵AD是△ABC的中线,
∴BD=CD.
在△ADC和△EDB中,
∴△ADC≌△EDB(SAS),
∴AC=BE.
∵AB-BE<AE<AB+BE,
∴AB-AC<2AD<AB+AC.
∵AB=8,AC=5,
∴1.5<AD<6.5.
故选:B
5.B
【详解】
A、∵∠1=∠2,AD为公共边,若AB=AC,则△ABD≌△ACD(SAS);故A不符合题意;
B、∵∠1=∠2,AD为公共边,若BD=CD,不符合全等三角形判定定理,不能判定△ABD≌△ACD;故B符合题意;
C、∵∠1=∠2,AD为公共边,若∠B=∠C,则△ABD≌△ACD(AAS);故C不符合题意;
D、∵∠1=∠2,AD为公共边,若∠BDA=∠CDA,则△ABD≌△ACD(ASA);故D不符合题意.
故选:B.
6.C
【详解】
解:①∵AD是△ABC的中线,
∴BD=CD,
∴△ABD和△ACD面积相等;故①正确;
②若在△ABC中,当AB≠AC时,AD不是∠BAC的平分线,即∠BAD≠∠CAD.即②不一定正确;
③∵AD是△ABC的中线,
∴BD=CD,
在△BDF和△CDE中,
∵BD=CD,∠BDF=∠CDE,DF=DE,
∴△BDF≌△CDE(SAS).故③正确;
④∵△BDF≌△CDE,
∴∠CED=∠BFD,
∴BF∥CE;故④正确;
⑤∵△BDF≌△CDE,
∴CE=BF,
∴只有当AE=BF时,CE=AE.故⑤不一定正确.
综上所述,正确的结论是:①③④,共有3个.
故选C.
7.B
【详解】
∵∠EAO+∠BAH=90°,∠EAO+∠AEO=90°,
∴∠BAH=∠AEO,
∵在△AEO和△BAH中,
,
∴△AEO≌△BAH(AAS),
同理△BCH≌△CDF(AAS),
∴AO=BG=3,AH=EO=6,CH=DF=4,BH=CF=3,
∵梯形DEOF的面积=(EF+DH) FH=80,
S△AEO=S△ABH=AF AE=9,
S△BCH=S△CDF=CH DH=6,
∴图中实线所围成的图形的面积S=80-2×9-2×6=50,
故选B.
8.D
【详解】
解:∵△ABC中,AD,BE分别为BC、AC边上的高,∠ABC=45°,
∴AD=BD,∠DAC和∠FBD都是∠ACD的余角,
而∠ADB=∠ADC=90°,
∴△BDF≌△ADC,
∴BF=AC,故①正确,
∴FD=CD,
∴∠FCD=∠CFD=45°,故②正确;
若BF=2EC,根据①得BF=AC,
∴AC=2EC,
即E为AC的中点,
∴BE为线段AC的垂直平分线,
∴AF=CF,BA=BC,
∴AB=BD+CD=AD+CD=AF+DF+CD=CF+DF+CD,
即△FDC周长等于AB的长,故③正确.
故选D.
9.D
【详解】
解:∵BF=CE,
∴BF+EF=CE+EF
∴BE=CF.
在△ABE和△DCF中, ,
∴△ABE≌△DCF(SSS);故①AE=DF,正确;
∵AE∥DF,
∴∠AEF=∠DFC.
∵在△ABE和△DCF中,AB=DC,BF=CE,
∴△ABE不一定和△DCF全等,故②AE∥DF,错误;;
∵AB∥DC,
∴∠B=∠C;
∴在△ABE和△DCF中,,
∴△ABE≌△DCF(SAS),故③AB∥DC,正确;
∵AB=DC,BF=CE,∠A=∠D,
∴△ABE不一定和△DCF全等,故④∠A=∠D,错误;;
∴①③
故选D.
10.B
【详解】
A.两边及夹角对应相等的两三角形全等,故此命题是假命题;
B.两角及一边对应相等的两三角形全等,故此命题是真命题;
C.三个角对应相等的两三角形,边长不一定相等,故此命题是假命题;
D.面积相等的两三角形不一定全等,故此命题是假命题.
故选:B.
11.AB=AC或∠B=∠C或∠BDA=∠CDA或∠BDE=∠CDE(四者选一即可)
【详解】
解:∵AE平分∠BAC,
∴∠BAD=∠CAD
∵AD=AD
再添加AB=AC,可用SAS证明△ABD≌△ACD;
再添加∠B=∠C,可用AAS证明△ABD≌△ACD;
再添加∠BDA=∠CDA,可用ASA证明△ABD≌△ACD;
再添加∠BDE=∠CDE,根据等角的补角相等,可得:∠BDA=∠CDA,可用ASA证明△ABD≌△ACD;
故答案为AB=AC或∠B=∠C或∠BDA=∠CDA或∠BDE=∠CDE(四者选一即可)
12.1.
【详解】
解:∵,∠BEA=∠DEC
∴∠ADC=∠BEA
在△ADC和△BEA中
∴△ADC≌△BEA
∴AC=BA
∵
∴AB-AE=1
∴CE=AC-AE=AB-AE=1
故答案为:1.
13.①②④.
【详解】
解:,
,故②正确;
AB=CD,,故④正确;
∠AEB=∠DEC,
,故①正确;
不成立,故③错误;正确的有①②④;
故答案为①②④.
14.①②④
【详解】
∵等边△ABD,等边△EBC,∴AB=BD=AD,BE=BC=EC,∠ABD=∠EBC=60°,
∴∠ABE=∠DBC,∠DBE=60°,
在△ABE和△DBC中,
,
∴△ABE≌△DBC,①说法正确;
由①可得:∠PAB=∠QDB,
在△DQB和△ABP中,
,
∴△DQB≌△ABP,②说法正确;
③说法不能证明,错误;
∠AMC=∠DAM+∠MDA=∠DAM+∠MDB+∠BDA=∠DAM+∠MAB+∠BDA=120°,④说法正确.
故答案为①②④.
点睛:本题关键利用等边三角形对应的边相等、角相等的性质证明三角形全等.
15.90°
【详解】
∵CD 、 BE 是边 AB 和 AC 上的高,
∴∠ADC=∠AEB=90° ,
∴∠ABM+∠BAC=90°,∠BAC+∠ACN=90° ,
∴∠ABM=∠ACN ,
在 △ABM 和 △ACN 中,
∵AB=CN,∠ABM=∠CAN,BM=AC ,
∴△ABM ≌ △NCA ,
∴∠BAM=∠CNA ,
∵∠CNA=∠ADC+∠BAN=90°+∠BAN , ∠BAM=∠MAN+∠BAN ,
∴∠MAN=90°.
故答案为 90°.
16.两直线平行,同位角相等;;SAS;全等三角形的判定与性质
【详解】
证明:(已知)
(两直线平行,同位角相等)
在和中,
,
(SAS),
(全等三角形的判定与性质).
17.图见解析,同位角相等,两直线平行
【详解】
解:在OM同侧作∠MAB=∠MON,则射线AB即为所要求画的,
∵∠MAB=∠MON,
∴ABON.
即同位角相等,两直线平行.
18.(1)见解析;(2)点在的平分线上,见解析
【详解】
(1)证明:∵、是两条高,
∴,
在和中,
,
∴≌(HL),
∴;
(2)解:点在的平分线上,
理由:连接AO,
∵在与中,
,
∴≌(AAS),
∴,
在和中,
,
∴≌(HL),
∴∠BAO=∠CAO,
∴点O在∠BAC的角平分线上.
19.证明见解析.
【详解】
证明:∵AB是∠DAC的平分线,
∴∠DAB=∠CAB,
在△ABD和△ABC中
∴△ABD≌△ABC(SAS).
∴BD=BC
20.见解析
【详解】
证明:∵AB∥CD,
∴∠BAC=∠ECD,
∵在△BAC和△ECD中,
AB=EC,∠BAC=∠ECD ,AC=CD,
∴△BAC≌△ECD(SAS).
∴CB=ED.
12.2 三角形全等的判定(同步练习)
一、单选题
1.下列说法错误的是( )
A.三边分别相等的两个三角形全等
B.三角分别相等的两个三角形全等
C.两边和它们的夹角分别相等的两个三角形全等
D.斜边和一条直角边分别相等的两个直角三角形全等
2.下列条件中,不能判定△ABC≌△A′B′C′,的是( )
A.∠A=∠A,∠C=∠C,AC=A′C′
B.∠B=∠B′,BC=B′C′,AB=A′B′
C.∠A=∠A′=80°,∠B=60°,∠C′=40°,AB=A′B′
D.∠A=∠A′,BC=B′C′,AB=A′B′
3.如图,在中,于点,于点,,交于点,≌.若,,则的面积为( ).
A.24 B.18 C.12 D.8
4.如图,在△ABC 中,AB=8,AC=5,AD是△ABC的中线,则AD的取值范围是( )
A.3
A.AB=AC B.BD=CD C.∠B=∠C D.∠BDA=∠CDA
6.如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连结BF,CE.下列说法:①△ABD和△ACD面积相等;②∠BAD=∠CAD;③△BDF≌△CDE;④BF∥CE;⑤CE=AE.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
7.如图,点A,C,D,E在Rt△MON的边上,∠MON=90°,AE⊥AB且AE=AB,BC⊥CD,BH⊥ON于点H,DF⊥ON于点F,OM=12,OE=6,BH=3,DF=4,FN=8,图中阴影部分的面积为( )
A.30 B.50 C.66 D.80
8.如图,在△ABC中,∠ABC=45°,AD,BE分别为BC、AC边上的高,AD、BE相交于点F,连接CF,则下列结论:①BF=AC; ②∠FCD=45°; ③若BF=2EC,则△FDC周长等于AB的长;其中正确的有( )
A.0个 B.1个 C.2个 D.3个
9.如图,AB=DC,BF=CE,需补充一个条件,就能使△ABE≌△DCF,小明给出以下四个答案:①AE=DF;②AE∥DF;③AB∥DC;④∠A=∠D,其中正确的是( )
A.①②③④ B.①②③ C.①② D.①③
10.下列命题是真命题的是( )
A.两边及一个角对应相等的两个三角形全等
B.两角及一边对应相等的两个三角形全等
C.三个角对应相等的两个三角形全等
D.面积相等的两个三角形全等
二、填空题
11.如图,已知AE平分∠BAC,点D是AE上一点,连接BD,CD.请你添加一个适当的条件,使△ABD≌△ACD.添加的条件是:____.(写出一个即可)
12.如图所示,已知AC与BD相交于点E,,,,,则CE的长为______
13.如图交于点E,下列①②③④正确的有________
14.如图,点A,B,C在同一直线上,在这条直线同侧作等边△ABD和等边△BCE,连接AE和CD,交点为M,AE交BD于点P,CD交BE于点Q,连接PQ、BM, 有4个结论:①△ABE≌△DBC,②△DQB≌△ABP,③∠EAC=30°,④∠AMC=120°,请将所有正确结论的序号填在横线上______.
15.如图,△ABC中,CD、BE是边AB和AC上的高,点M在BE的延长线上,且BM=AC,点N在CD上,且AB=CN,则∠MAN的度数是________.
三、解答题
16.已知:如图,点B、E、C、F在同一条直线上,且,,.求证:.请将下面的过程和理由补充完整.
证明:(已知)
(___________)
在和中,
(________)
(_________)
17.作图题:如图,已知ON是一条公路桥梁,现要在上游点A处再建一座与ON平行的大桥AB,请用尺规画出AB方向(不必写作法).并根据你的作法用一句话简单说明为什么AB和ON是平行的?
18.如图,的两条高、相交于点,.
(1)求证:;
(2)判断点是否在的平分线上,并说明理由.
19.如图,AB是∠DAC的平分线,且AD=AC.
求证:BD=BC.
20.已知:如图,点E,A,C在同一条直线上,AB∥CD,AB=CE,AC=CD.
求证:BC=ED.
参考答案:
1.B
【详解】
解:A、三边分别相等的两个三角形全等,此项说法正确;
B、三角分别相等的两个三角形全等,此项说法错误;
C、两边和它们的夹角分别相等的两个三角形全等,此项说法正确;
D、斜边和一条直角边分别相等的两个直角三角形全等,此项说法正确;
故选:B.
2.D
【详解】
试题分析:根据三角形全等的判定方法,SSS、SAS、ASA、AAS,逐一检验.
考点:全等三角形的判定
3.C
【详解】
∵,
∴AD=BD=4,
∵BC=BD+CD=4+2=6,
∴
故选C.
4.B
【详解】
解:延长AD到E,使AD=DE,连结BE.
∵AD是△ABC的中线,
∴BD=CD.
在△ADC和△EDB中,
∴△ADC≌△EDB(SAS),
∴AC=BE.
∵AB-BE<AE<AB+BE,
∴AB-AC<2AD<AB+AC.
∵AB=8,AC=5,
∴1.5<AD<6.5.
故选:B
5.B
【详解】
A、∵∠1=∠2,AD为公共边,若AB=AC,则△ABD≌△ACD(SAS);故A不符合题意;
B、∵∠1=∠2,AD为公共边,若BD=CD,不符合全等三角形判定定理,不能判定△ABD≌△ACD;故B符合题意;
C、∵∠1=∠2,AD为公共边,若∠B=∠C,则△ABD≌△ACD(AAS);故C不符合题意;
D、∵∠1=∠2,AD为公共边,若∠BDA=∠CDA,则△ABD≌△ACD(ASA);故D不符合题意.
故选:B.
6.C
【详解】
解:①∵AD是△ABC的中线,
∴BD=CD,
∴△ABD和△ACD面积相等;故①正确;
②若在△ABC中,当AB≠AC时,AD不是∠BAC的平分线,即∠BAD≠∠CAD.即②不一定正确;
③∵AD是△ABC的中线,
∴BD=CD,
在△BDF和△CDE中,
∵BD=CD,∠BDF=∠CDE,DF=DE,
∴△BDF≌△CDE(SAS).故③正确;
④∵△BDF≌△CDE,
∴∠CED=∠BFD,
∴BF∥CE;故④正确;
⑤∵△BDF≌△CDE,
∴CE=BF,
∴只有当AE=BF时,CE=AE.故⑤不一定正确.
综上所述,正确的结论是:①③④,共有3个.
故选C.
7.B
【详解】
∵∠EAO+∠BAH=90°,∠EAO+∠AEO=90°,
∴∠BAH=∠AEO,
∵在△AEO和△BAH中,
,
∴△AEO≌△BAH(AAS),
同理△BCH≌△CDF(AAS),
∴AO=BG=3,AH=EO=6,CH=DF=4,BH=CF=3,
∵梯形DEOF的面积=(EF+DH) FH=80,
S△AEO=S△ABH=AF AE=9,
S△BCH=S△CDF=CH DH=6,
∴图中实线所围成的图形的面积S=80-2×9-2×6=50,
故选B.
8.D
【详解】
解:∵△ABC中,AD,BE分别为BC、AC边上的高,∠ABC=45°,
∴AD=BD,∠DAC和∠FBD都是∠ACD的余角,
而∠ADB=∠ADC=90°,
∴△BDF≌△ADC,
∴BF=AC,故①正确,
∴FD=CD,
∴∠FCD=∠CFD=45°,故②正确;
若BF=2EC,根据①得BF=AC,
∴AC=2EC,
即E为AC的中点,
∴BE为线段AC的垂直平分线,
∴AF=CF,BA=BC,
∴AB=BD+CD=AD+CD=AF+DF+CD=CF+DF+CD,
即△FDC周长等于AB的长,故③正确.
故选D.
9.D
【详解】
解:∵BF=CE,
∴BF+EF=CE+EF
∴BE=CF.
在△ABE和△DCF中, ,
∴△ABE≌△DCF(SSS);故①AE=DF,正确;
∵AE∥DF,
∴∠AEF=∠DFC.
∵在△ABE和△DCF中,AB=DC,BF=CE,
∴△ABE不一定和△DCF全等,故②AE∥DF,错误;;
∵AB∥DC,
∴∠B=∠C;
∴在△ABE和△DCF中,,
∴△ABE≌△DCF(SAS),故③AB∥DC,正确;
∵AB=DC,BF=CE,∠A=∠D,
∴△ABE不一定和△DCF全等,故④∠A=∠D,错误;;
∴①③
故选D.
10.B
【详解】
A.两边及夹角对应相等的两三角形全等,故此命题是假命题;
B.两角及一边对应相等的两三角形全等,故此命题是真命题;
C.三个角对应相等的两三角形,边长不一定相等,故此命题是假命题;
D.面积相等的两三角形不一定全等,故此命题是假命题.
故选:B.
11.AB=AC或∠B=∠C或∠BDA=∠CDA或∠BDE=∠CDE(四者选一即可)
【详解】
解:∵AE平分∠BAC,
∴∠BAD=∠CAD
∵AD=AD
再添加AB=AC,可用SAS证明△ABD≌△ACD;
再添加∠B=∠C,可用AAS证明△ABD≌△ACD;
再添加∠BDA=∠CDA,可用ASA证明△ABD≌△ACD;
再添加∠BDE=∠CDE,根据等角的补角相等,可得:∠BDA=∠CDA,可用ASA证明△ABD≌△ACD;
故答案为AB=AC或∠B=∠C或∠BDA=∠CDA或∠BDE=∠CDE(四者选一即可)
12.1.
【详解】
解:∵,∠BEA=∠DEC
∴∠ADC=∠BEA
在△ADC和△BEA中
∴△ADC≌△BEA
∴AC=BA
∵
∴AB-AE=1
∴CE=AC-AE=AB-AE=1
故答案为:1.
13.①②④.
【详解】
解:,
,故②正确;
AB=CD,,故④正确;
∠AEB=∠DEC,
,故①正确;
不成立,故③错误;正确的有①②④;
故答案为①②④.
14.①②④
【详解】
∵等边△ABD,等边△EBC,∴AB=BD=AD,BE=BC=EC,∠ABD=∠EBC=60°,
∴∠ABE=∠DBC,∠DBE=60°,
在△ABE和△DBC中,
,
∴△ABE≌△DBC,①说法正确;
由①可得:∠PAB=∠QDB,
在△DQB和△ABP中,
,
∴△DQB≌△ABP,②说法正确;
③说法不能证明,错误;
∠AMC=∠DAM+∠MDA=∠DAM+∠MDB+∠BDA=∠DAM+∠MAB+∠BDA=120°,④说法正确.
故答案为①②④.
点睛:本题关键利用等边三角形对应的边相等、角相等的性质证明三角形全等.
15.90°
【详解】
∵CD 、 BE 是边 AB 和 AC 上的高,
∴∠ADC=∠AEB=90° ,
∴∠ABM+∠BAC=90°,∠BAC+∠ACN=90° ,
∴∠ABM=∠ACN ,
在 △ABM 和 △ACN 中,
∵AB=CN,∠ABM=∠CAN,BM=AC ,
∴△ABM ≌ △NCA ,
∴∠BAM=∠CNA ,
∵∠CNA=∠ADC+∠BAN=90°+∠BAN , ∠BAM=∠MAN+∠BAN ,
∴∠MAN=90°.
故答案为 90°.
16.两直线平行,同位角相等;;SAS;全等三角形的判定与性质
【详解】
证明:(已知)
(两直线平行,同位角相等)
在和中,
,
(SAS),
(全等三角形的判定与性质).
17.图见解析,同位角相等,两直线平行
【详解】
解:在OM同侧作∠MAB=∠MON,则射线AB即为所要求画的,
∵∠MAB=∠MON,
∴ABON.
即同位角相等,两直线平行.
18.(1)见解析;(2)点在的平分线上,见解析
【详解】
(1)证明:∵、是两条高,
∴,
在和中,
,
∴≌(HL),
∴;
(2)解:点在的平分线上,
理由:连接AO,
∵在与中,
,
∴≌(AAS),
∴,
在和中,
,
∴≌(HL),
∴∠BAO=∠CAO,
∴点O在∠BAC的角平分线上.
19.证明见解析.
【详解】
证明:∵AB是∠DAC的平分线,
∴∠DAB=∠CAB,
在△ABD和△ABC中
∴△ABD≌△ABC(SAS).
∴BD=BC
20.见解析
【详解】
证明:∵AB∥CD,
∴∠BAC=∠ECD,
∵在△BAC和△ECD中,
AB=EC,∠BAC=∠ECD ,AC=CD,
∴△BAC≌△ECD(SAS).
∴CB=ED.
