2022-2023学年人教版数学九年级上册24.1.4圆周角 同步练习(Word版含答案)
文档属性
| 名称 | 2022-2023学年人教版数学九年级上册24.1.4圆周角 同步练习(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 671.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-27 08:29:05 | ||
图片预览




文档简介
24.1.4圆周角 同步练习
一、单选题
1.下列关于圆的叙述正确的有( )
圆内接四边形的对角互补;
相等的圆周角所对的弧相等;
正多边形内切圆的半径与正多边形的半径相等;
同圆中的平行弦所夹的弧相等.
A.1个 B.2个 C.3个 D.4个
2.如图,AC是⊙O的直径,弦AB//CD,若∠BAC=32°,则∠AOD等于( )
A.64° B.48° C.32° D.76°
3.如图,点A、B、C在⊙O上,且∠ACB=100o,则∠α度数为( )
A.160o B.120o C.100o D.80o
4.将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A,B的读数分别为86°,30°,则∠ACB的度数是( )
A.28° B.30° C.36° D.56°
5.如图,AB、CD分别是⊙O的直径,连接BC、BD,如果弦,且∠CDE=62°,则下列结论错误的是( )
A.CB⊥BD B.∠CBA=31° C. D.BD=DE
6.如图,在以AB为直径的⊙O中,点C为圆上的一点,,弦于点E,弦AF交CE于点H,交BC于点G,若点H是AG的中点,则的度数为( )
A.18° B.21° C.22.5° D.30°
7.如图,在中,,AB=AC=5,点在上,且,点E是AB上的动点,连结,点,G分别是BC,DE的中点,连接,,当AG=FG时,线段长为( )
A. B. C. D.4
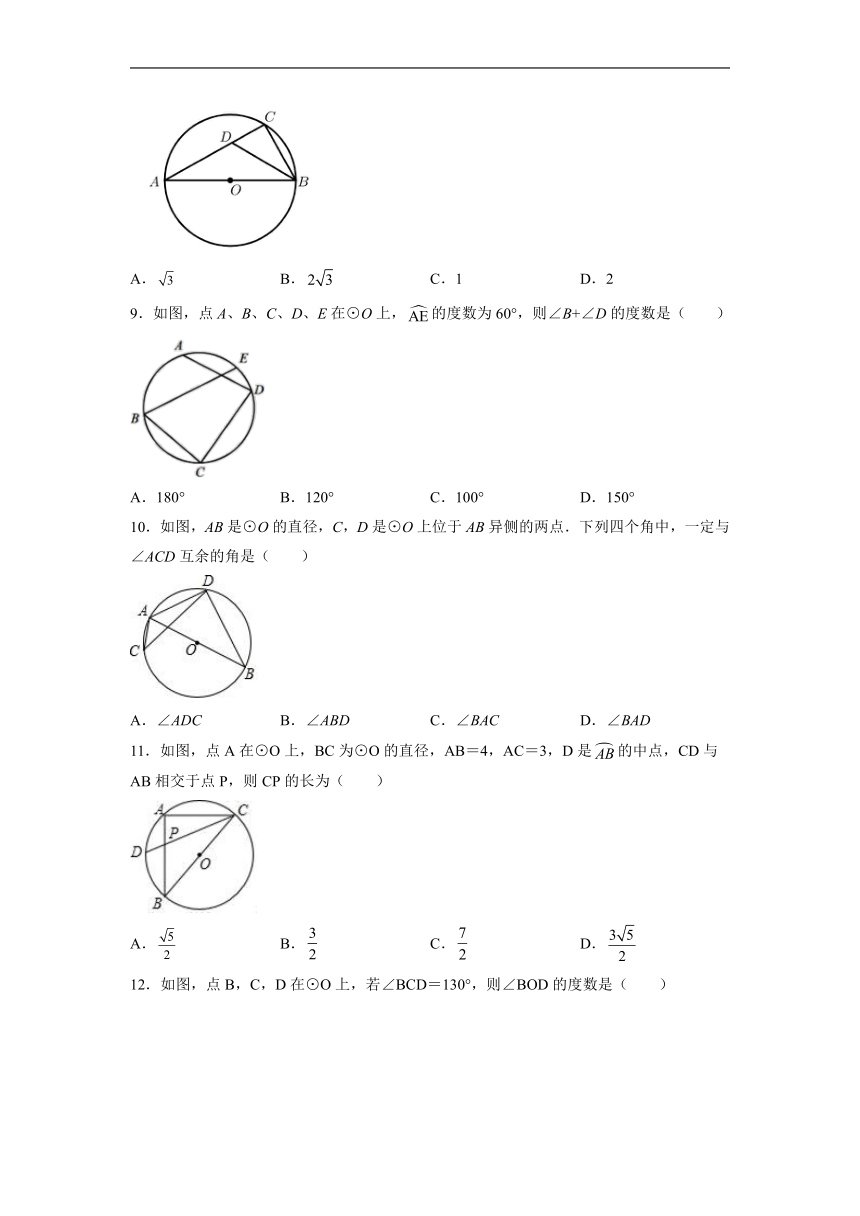
8.如图,是⊙的直径,点C为圆上一点,的平分线交于点D,,则⊙的直径为( )
A. B. C.1 D.2
9.如图,点A、B、C、D、E在⊙O上,的度数为60°,则∠B+∠D的度数是( )
A.180° B.120° C.100° D.150°
10.如图,AB是⊙O的直径,C,D是⊙O上位于AB异侧的两点.下列四个角中,一定与∠ACD互余的角是( )
A.∠ADC B.∠ABD C.∠BAC D.∠BAD
11.如图,点A在⊙O上,BC为⊙O的直径,AB=4,AC=3,D是的中点,CD与AB相交于点P,则CP的长为( )
A. B. C. D.
12.如图,点B,C,D在⊙O上,若∠BCD=130°,则∠BOD的度数是( )
A.50° B.60° C.80° D.100°
二、填空题
13.如图,圆O的直径AB垂直于弦CD,垂足是E,∠A=22.5°,OC=4,CD的长为 ___.
14.如图,在⊙O中,CD是直径,弦ABCD,垂足为E,连接BC,若AB=cm,,则圆O的半径为_______cm.
15.如图,AB为△ADC的外接圆⊙O的直径,若∠BAD=50°,则∠ACD=_____°.
16.如图,已知是的直径,且,弦,点是弧上的点,连接、,若,则的长为______.
17.如图,⊙O是△ABC的外接圆,∠A=60°,BC=6,则⊙O的半径是_____.
三、解答题
18.如图,⊙O的半径弦AB于点C,连结AO并延长交⊙O于点E,连结EC.已知,.
(1)求⊙O半径的长;
(2)求EC的长.
19.如图,AB是⊙O的直径,弦CD⊥AB于点E,点M在⊙O上,MD经过圆心O,连接MB.
(1)若CD=16,BE=4,求⊙O的半径;
(2)若∠M=∠D,求∠D的度数.
20.如图,△ABC内接于⊙O,∠A = 30°,过圆心O作OD⊥BC,垂足为D.若⊙O的半径为6,求OD的长.
21.如图,在⊙O中,弦AB,CD互相垂直,垂足为M,F是上的一点,且,AF分别与CD,BD相交于点E,N,连接FD,MN.
(1)求证:DE=DF;
(2)若⊙O的半径为8,∠BAF=22.5°,求线段MN的长.
参考答案
1--10BAAAD DABDD 11--12DD
13.4 14.2 15.40 16.9 17.6
18.解:(1)∵,
∴
∴设的半径
∴
∵在中,
∴
∴
∴半径的长为.
(2)连接,如图:
∵是的直径
∴,
∵
∴在中,
∵
∴在中,
∴.
19.解:(1),,
,
设,则
又,
,
解得:,
的半径是10.
(2),,
,
,
.
20.连接OB、OC,如图
则OB=OC=6
∵圆周角∠A与圆心角∠BOC对着同一段弧
∴∠BOC=2∠A=60゜
∴△OBC是等边三角形
∴BC=OB=6
∵OD⊥BC
∴
在Rt△ODC中,由勾股定理得:
21.(1),
,
,
,
,
,
,
,
,
,
;
(2)如图,连接,
,
,
,
,
,
在中,,
由(1)得,,
是等腰三角形,
,
,
是的中点,
,
,
,
,
,
.
一、单选题
1.下列关于圆的叙述正确的有( )
圆内接四边形的对角互补;
相等的圆周角所对的弧相等;
正多边形内切圆的半径与正多边形的半径相等;
同圆中的平行弦所夹的弧相等.
A.1个 B.2个 C.3个 D.4个
2.如图,AC是⊙O的直径,弦AB//CD,若∠BAC=32°,则∠AOD等于( )
A.64° B.48° C.32° D.76°
3.如图,点A、B、C在⊙O上,且∠ACB=100o,则∠α度数为( )
A.160o B.120o C.100o D.80o
4.将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A,B的读数分别为86°,30°,则∠ACB的度数是( )
A.28° B.30° C.36° D.56°
5.如图,AB、CD分别是⊙O的直径,连接BC、BD,如果弦,且∠CDE=62°,则下列结论错误的是( )
A.CB⊥BD B.∠CBA=31° C. D.BD=DE
6.如图,在以AB为直径的⊙O中,点C为圆上的一点,,弦于点E,弦AF交CE于点H,交BC于点G,若点H是AG的中点,则的度数为( )
A.18° B.21° C.22.5° D.30°
7.如图,在中,,AB=AC=5,点在上,且,点E是AB上的动点,连结,点,G分别是BC,DE的中点,连接,,当AG=FG时,线段长为( )
A. B. C. D.4
8.如图,是⊙的直径,点C为圆上一点,的平分线交于点D,,则⊙的直径为( )
A. B. C.1 D.2
9.如图,点A、B、C、D、E在⊙O上,的度数为60°,则∠B+∠D的度数是( )
A.180° B.120° C.100° D.150°
10.如图,AB是⊙O的直径,C,D是⊙O上位于AB异侧的两点.下列四个角中,一定与∠ACD互余的角是( )
A.∠ADC B.∠ABD C.∠BAC D.∠BAD
11.如图,点A在⊙O上,BC为⊙O的直径,AB=4,AC=3,D是的中点,CD与AB相交于点P,则CP的长为( )
A. B. C. D.
12.如图,点B,C,D在⊙O上,若∠BCD=130°,则∠BOD的度数是( )
A.50° B.60° C.80° D.100°
二、填空题
13.如图,圆O的直径AB垂直于弦CD,垂足是E,∠A=22.5°,OC=4,CD的长为 ___.
14.如图,在⊙O中,CD是直径,弦ABCD,垂足为E,连接BC,若AB=cm,,则圆O的半径为_______cm.
15.如图,AB为△ADC的外接圆⊙O的直径,若∠BAD=50°,则∠ACD=_____°.
16.如图,已知是的直径,且,弦,点是弧上的点,连接、,若,则的长为______.
17.如图,⊙O是△ABC的外接圆,∠A=60°,BC=6,则⊙O的半径是_____.
三、解答题
18.如图,⊙O的半径弦AB于点C,连结AO并延长交⊙O于点E,连结EC.已知,.
(1)求⊙O半径的长;
(2)求EC的长.
19.如图,AB是⊙O的直径,弦CD⊥AB于点E,点M在⊙O上,MD经过圆心O,连接MB.
(1)若CD=16,BE=4,求⊙O的半径;
(2)若∠M=∠D,求∠D的度数.
20.如图,△ABC内接于⊙O,∠A = 30°,过圆心O作OD⊥BC,垂足为D.若⊙O的半径为6,求OD的长.
21.如图,在⊙O中,弦AB,CD互相垂直,垂足为M,F是上的一点,且,AF分别与CD,BD相交于点E,N,连接FD,MN.
(1)求证:DE=DF;
(2)若⊙O的半径为8,∠BAF=22.5°,求线段MN的长.
参考答案
1--10BAAAD DABDD 11--12DD
13.4 14.2 15.40 16.9 17.6
18.解:(1)∵,
∴
∴设的半径
∴
∵在中,
∴
∴
∴半径的长为.
(2)连接,如图:
∵是的直径
∴,
∵
∴在中,
∵
∴在中,
∴.
19.解:(1),,
,
设,则
又,
,
解得:,
的半径是10.
(2),,
,
,
.
20.连接OB、OC,如图
则OB=OC=6
∵圆周角∠A与圆心角∠BOC对着同一段弧
∴∠BOC=2∠A=60゜
∴△OBC是等边三角形
∴BC=OB=6
∵OD⊥BC
∴
在Rt△ODC中,由勾股定理得:
21.(1),
,
,
,
,
,
,
,
,
,
;
(2)如图,连接,
,
,
,
,
,
在中,,
由(1)得,,
是等腰三角形,
,
,
是的中点,
,
,
,
,
,
.
同课章节目录
