2022--2023学年北师大版八年级数学上册3.2平面直角坐标系 同步复习小测(Word版含答案)
文档属性
| 名称 | 2022--2023学年北师大版八年级数学上册3.2平面直角坐标系 同步复习小测(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 307.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-27 00:00:00 | ||
图片预览



文档简介
3.2平面直角坐标系---八年级同步复习小测(同步训练+课后作业)
【北师大版】
【同步训练】
一、单选题
1.象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏,如图,若表示棋子“馬”和“車”的点的坐标分别为( , ),(﹣ , ),则表示棋子“炮”的点的坐标为( )
A.(1,2) B.(0,2) C.(2,1) D.(2,0)
2.在平面直角坐标系中,点(﹣2,﹣2m+3)在第三象限,则m的取值范围是( )
A. B. C. D.
3.如图,在平面直角坐标系中,点A的坐标是(﹣3,0),点B的坐标是(0,4),点M是OB上一点,将 ABM沿AM折叠,点B恰好落在x轴上的点 处,则点M的坐标为( )
A.( ,0) B.(0, ) C.( ,0) D.(0, )
4.若点 到y轴的距离是它到x轴距离的两倍,则( ).
A. B. C. D.
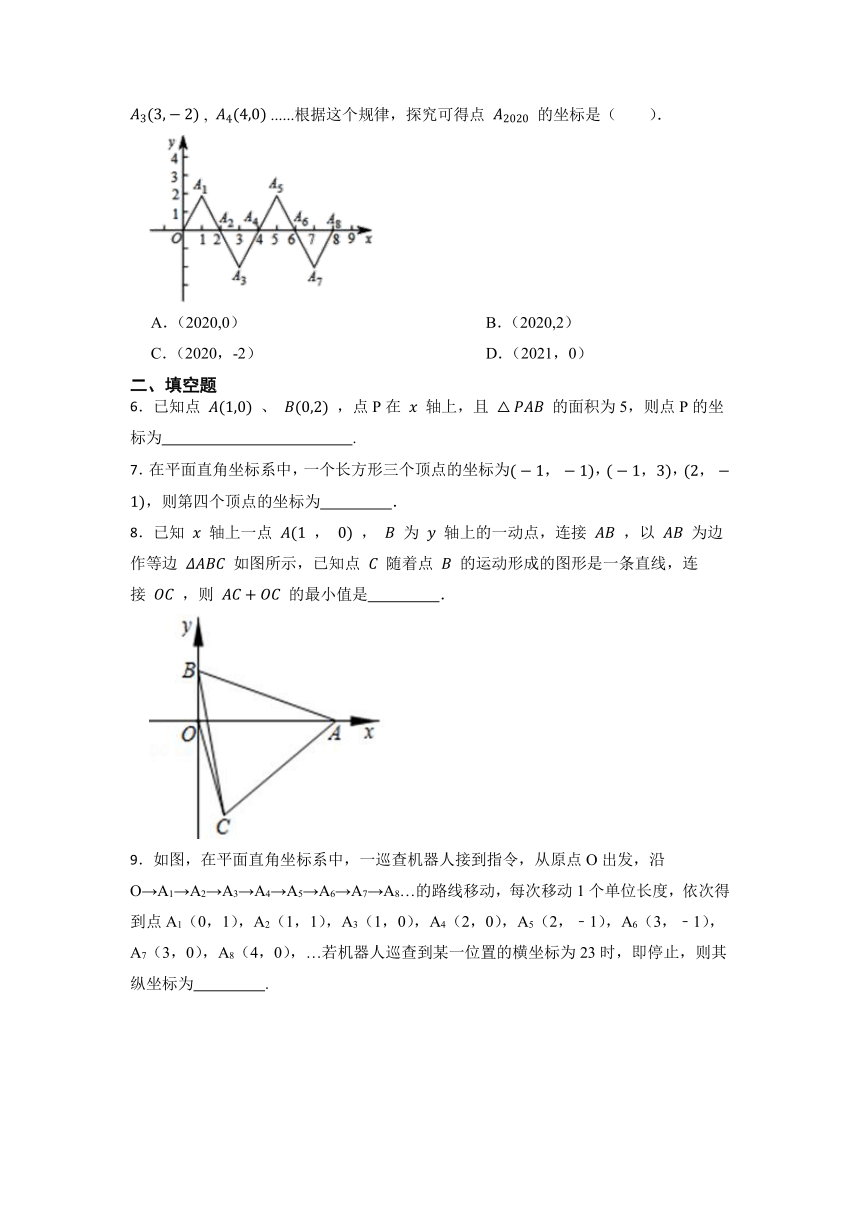
5.如图,在平面直角坐标系中,点根据这个规律,探究可得点 , , , ......根据这个规律,探究可得点 的坐标是( ).
A.(2020,0) B.(2020,2)
C.(2020,-2) D.(2021,0)
二、填空题
6.已知点 、 ,点P在 轴上,且 的面积为5,则点P的坐标为 .
7.在平面直角坐标系中,一个长方形三个顶点的坐标为,,,则第四个顶点的坐标为 .
8.已知 轴上一点 , , 为 轴上的一动点,连接 ,以 为边作等边 如图所示,已知点 随着点 的运动形成的图形是一条直线,连接 ,则 的最小值是 .
9.如图,在平面直角坐标系中,一巡查机器人接到指令,从原点O出发,沿O→A1→A2→A3→A4→A5→A6→A7→A8…的路线移动,每次移动1个单位长度,依次得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),A5(2,﹣1),A6(3,﹣1),A7(3,0),A8(4,0),…若机器人巡查到某一位置的横坐标为23时,即停止,则其纵坐标为 .
三、解答题
10.在平面直角坐标系内,已知点Q(m+3,2m+4)在x轴上,求m的值及点Q的坐标?
11.若点 的横纵坐标同号,且点P到两坐标轴的距离相等,求 的平方根,
12.阅读与理解:
如图,一只甲虫在5×5的方格(每个方格边长均为1)上沿着网格线爬行.若我们规定:在如图网格中,向上(或向右)爬行记为“+”,向下(或向左)爬行记为“-”,并且第一个数表示左右方向,第二个数表示上下方向。
例如:从A到B记为:A→B(+1,+4),
从D到C记为:D→C(-1,+2)。
思考与应用:
(1)图中A→C( , );
B→C( , );
D→A( , )。
(2)若甲虫从A到P的行走路线依次为:(+3,+2)→(+1,+3)→(+1,-2),请在图中标出P的位置。
(3)若甲虫的行走路线为A一(+1,+4)→(+2,0)→(+1,-2)-(-4,-2),请计算该甲虫走过的总路程。
13.如图,在平面直角坐标系中,矩形 的边 在 轴上,顶点 , ,连接 ,按下列方法作图:
(1)以点 为圆心,适当长为半径画弧,分别交 、 于点 , ;
(2)分别以点 , 为圆心,大于 的长为半径画弧两弧交于点 ;
(3)作射线 交 于点 ,则点 的横坐标为( )
A.
B.
C.1
D.
【课后作业】
一、单选题
1.若x轴上的点P到y轴的距离为3,则点P的坐标为( )
A.(3,0) B.(3,0)或(–3,0)
C.(0,3) D.(0,3)或(0,–3)
2.在平面直角坐标系中,点,,,若轴,则线段BC的最小值及此时点C的坐标分别为( )
A.3, B.10,
C.1, D.6,
3.对平面上任意一点(a,b),定义f,g两种变换:f(a,b)=(a,﹣b).如f(1,2)=(1,﹣2);g(a,b)=(b,a).如g(1,2)=(2,1).据此得g(f(5,﹣9))=( )
A.(5,﹣9) B.(﹣9,﹣5)
C.(5,9) D.(9,5)
4.已知点A的坐标为(2,-1),则点A到原点的距离为( )
A.3 B. C. D.1
5.如果点A(m,n)在第三象限,那么点B(0,m+n)在 ( )
A.x轴正半轴上 B.x轴负半轴上 C.y轴正半轴上 D.y轴负半轴上
二、填空题
6.若M(4,2),点N(4,5),则直线 与 轴平行.
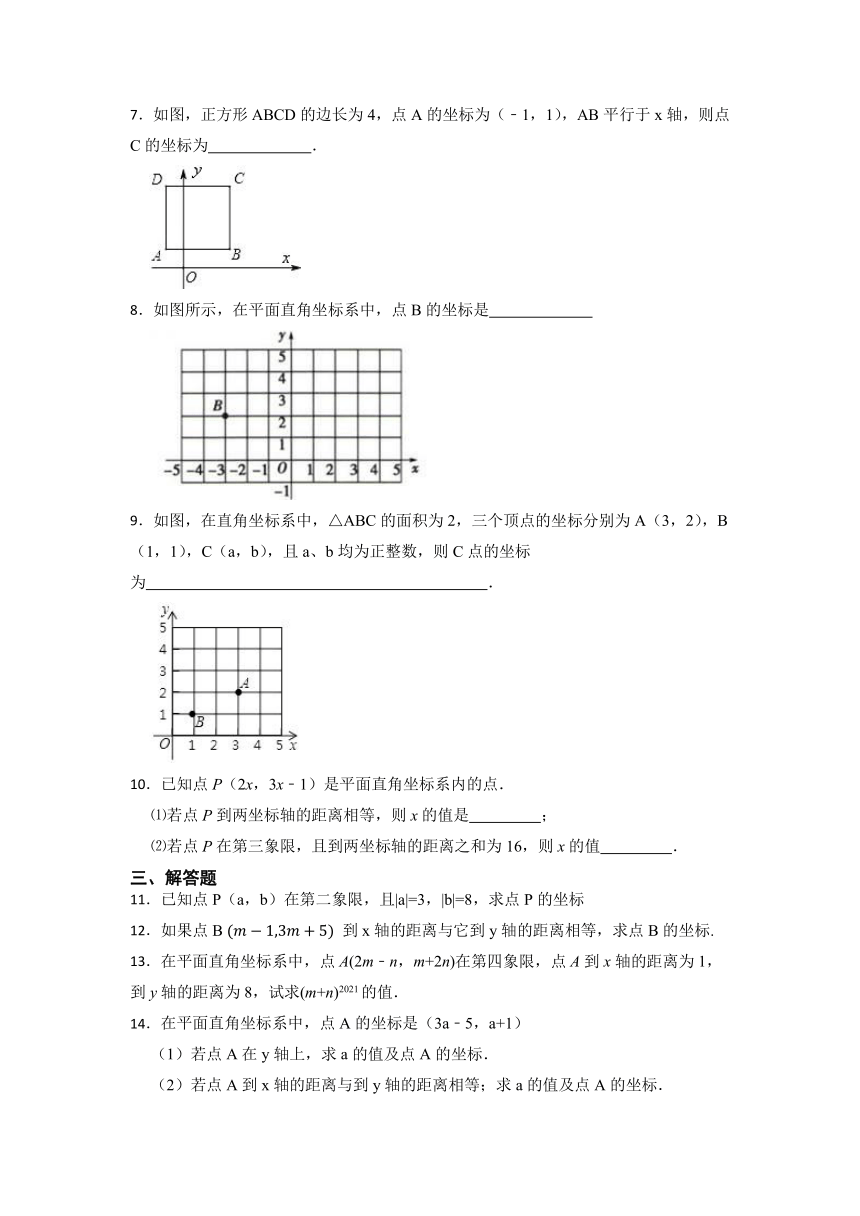
7.如图,正方形ABCD的边长为4,点A的坐标为(﹣1,1),AB平行于x轴,则点C的坐标为 .
8.如图所示,在平面直角坐标系中,点B的坐标是
9.如图,在直角坐标系中,△ABC的面积为2,三个顶点的坐标分别为A(3,2),B(1,1),C(a,b),且a、b均为正整数,则C点的坐标为 .
10.已知点P(2x,3x﹣1)是平面直角坐标系内的点.
⑴若点P到两坐标轴的距离相等,则x的值是 ;
⑵若点P在第三象限,且到两坐标轴的距离之和为16,则x的值 .
三、解答题
11.已知点P(a,b)在第二象限,且|a|=3,|b|=8,求点P的坐标
12.如果点B 到x轴的距离与它到y轴的距离相等,求点B的坐标.
13.在平面直角坐标系中,点A(2m﹣n,m+2n)在第四象限,点A到x轴的距离为1,到y轴的距离为8,试求(m+n)2021的值.
14.在平面直角坐标系中,点A的坐标是(3a﹣5,a+1)
(1)若点A在y轴上,求a的值及点A的坐标.
(2)若点A到x轴的距离与到y轴的距离相等;求a的值及点A的坐标.
【同步训练答案】
1.【答案】B
【解析】【解答】解:根据棋子“馬”和“車”的点的坐标可建立直角坐标系,如图所示:
故棋子“炮”的点的坐标为:(0,2).
故答案为:B.
【分析】根据题目描述找出x轴、y轴及原点,画出直角坐标系,得出棋子“炮”的点的坐标 .
2.【答案】B
【解析】【解答】解:∵点在第三象限,
∴点的横坐标是负数,纵坐标也是负数,
即﹣2m+3<0,
解得m>.
故选B.
【分析】点在第三象限的条件是:横坐标是负数,纵坐标是负数,可得﹣2m+3<0,求不等式的解即可.
3.【答案】B
【解析】【解答】解:设 ,则 ,
由题意可得: , ,
由勾股定理得: ,
由勾股定理可得: ,即
解得 , ,即
故答案为:B.
【分析】设BM=x,在直角三角形ABO中,用勾股定理可求得AB的值,在直角三角形B OM中,用勾股定理可得关于x的方程,解方程求得x的值,于是OM=OB-BM可求解.
4.【答案】C
【解析】【解答】解:点 到y轴的距离是它到x轴距离的两倍.则 ,
故答案为:C.
【分析】点到x轴的距离为纵坐标的绝对值,到y轴的距离为横坐标的绝对值,据此即可得到m、n的关系.
5.【答案】A
【解析】【解答】通过观察发现,点的横坐标依次是0,1,2,3,……,点的纵坐标为2,0,-2,0四个数一循环,
∵ ,
∴ 的横坐标为2020,纵坐标为0,
∴点 的坐标是(2020,0).
故答案为:A.
【分析】观察点的横纵坐标的特点,找出规律,利用规律即可得出答案.
6.【答案】(-4,0)或(6,0)
【解析】【解答】解:如图,设P(m,0),
由题意: |1-m| 2=5,
∴m=-4或6,
∴P(-4,0)或(6,0),
故答案为:(-4,0)或(6,0)
【分析】设P(m,0),利用三角形的面积公式构建绝对值方程求出m即可;
7.【答案】
【解析】【解答】点和的横坐标相等,
点和的纵坐标相等,
要使这四个点构成矩形,则第四个点的横坐标与相等,纵坐标与相等,
∴第四个顶点的坐标为;
故答案是.
【分析】根据长方形的性质,分析各点坐标之间关系即可求出第四个顶点的坐标。
8.【答案】
【解析】【解答】解:如图,在第四象限以OA为长作等边△AOD,连接OD,并作直线CD延长AD交y轴于点A'
∵等边△ABC,等边△AOD
∴AB=AC,AO=AD,∠BAC=∠OAD=60°
∴∠BAC-∠OAC=∠OAD-∠OAC
∴∠BAO=∠CAD
在△BAO和△CAD中
∴△BAO≌△CAD(SAS)
∴∠AOB=∠ADC
∵∠AOB=90°
∴∠ADC=90°
∴CD⊥AD,
∴点C随着点B的运动形成的图形是直线CD
∵∠AOA'=90°,∠OAD=60°
∴∠AA'O=30°
∴OA=AA'
∴AD=OA=AA'
∴ 点D是AA'的中点,
∴CD垂直平分AA'
∴AC=A'C
∴AC+OC=A'C+OC
∵点C在直线CD上运动,所以点O、C、A'三点共线时,A'C+OC的值最小,最小值为OA'的长
在Rt△AOA'中,∠OAD=60°,OA=1
∴OA'=OAtan60°=
∴AC+OC的最小值为
故答案为:
【分析】 根据题意,在第四象限以OA为边作等边△AOD,连接OD,作直线CD,延长AD交y轴于点A',利用等边三角形的性质,可证得AB=AC,AO=AD,∠BAC=∠OAD,即可证得∠BAO=∠CAD,再利用SAS证明△BAO≌△CAD,利用全等三角形的性质,去证明CD⊥AD,再由点C随着点B的运动形成的图形是直线CD,易证CD垂直平分AA', 利用垂直平分线的性质,可证AC=A'C,点C在直线CD上运动,所以点O、C、A'三点共线时,A'C+OC的值最小,最小值为OA'的长,然后利用解直角三角形求出OA'的长即可求解。
9.【答案】﹣1
【解析】【解答】由题可知,纵坐标从O到A8是一组循环,
23÷9=2…5,
∴横坐标是23时,移动到的位置与点A5的位置相同,
∴纵坐标是﹣1;
故答案为﹣1.
【分析】由图可知:纵坐标从O到A8是一组循环,然后即可算出横坐标是23时,移动到的位置与点A5的位置相同,
10.【答案】解:∵点Q(m+3,2m+4)在x轴上,
∴2m+4=0,
解得m=﹣2,
∴m+3=﹣2+3=1,
∴点Q的坐标为(1,0).
【解析】【分析】根据x轴上点的纵坐标为0列方程求解即可得到m的值,然后求解即可得到点Q的坐标.
11.【答案】解:由题意,得 ,解得 ,
故 ,
的平方根为
【解析】【分析】由题意得1-a=2a+7,解得a=-2,故6-5a=16,所以6-5a的平方根为±4.
12.【答案】(1)+3;+4;+2;0;﹣4;﹣2
(2)解:如图2所示.
(3)解:甲虫走过的总路程:
|+1|+|+4|+|+2|+|+1|+|﹣2|+|﹣4|+|﹣2|=16.
【解析】【分析】(1)根据题意,可依次表示出行走方向。
(2)根据所走的路线,可找出P的位置。
(3)根据行走路线,计算得出总路程。
13.【答案】;A
【解析】【解答】解:过 点作 于 ,如图,
由作法得 平分 ,
,
矩形 的顶点 的坐标为 , 点坐标为 ,
, ,
在 中, ,
在 和 中,
,
∴ ,
,
,
设 ,则 , ,
在 中, ,
解得 ,
即 ,
点的横坐标为 .
故答案为:A.
【分析】过点H作MH⊥AC于点M,利用角平分线的性质可证得MH=HD;利用矩形的性质可求出AB,BC的长,利用勾股定理求出AC的长;再利用HL证明Rt△CHD≌Rt△CHM,由此可求出CM的长;根据AM=AC-CM,可求出AM的长;设DH=t,可表示出AH,HM的长,利用勾股定理建立关于t的方程,解方程求出t的值,即可得到HD的长,由此可得到点H的横坐标.
【课后作业答案】
1.【答案】B
【解析】【分析】根据x轴上的点P到y轴的距离为3,可得点P的横坐标为±3,进而根据x轴上点的纵坐标为0可得具体坐标.
【解答】∵x轴上的点P到y轴的距离为3,
∴点P的横坐标为±3,
∵x轴上点的纵坐标为0,
∴点P的坐标为(3,0)或(-3,0),
故选:B.
【点评】本题考查了点的坐标的相关知识;用到的知识点为:x轴上点的纵坐标为0
2.【答案】A
【解析】【解答】解:依题意可得:
∵AC∥x轴,A(-3,2)
∴y=2,
根据垂线段最短,当BC⊥AC于点C时,
点B到AC的距离最短,即BC的最小值=5-2=3,
此时点C的坐标为(3,2),
故答案为:A.
【分析】根据点坐标的定义及垂线段最短的性质可得答案。
3.【答案】D
【解析】【分析】根据两种变换的规则,先计算f(5,﹣9)=(5,9),再计算g(5,9)即可。
【解答】g(f(5,﹣9))=g(5,9)=(9,5).
故选D.
4.【答案】C
【解析】【解答】解:∵点A的坐标为(2,-1),
∴点A到原点O的距离OA ,
故答案为:C
【分析】由点A的坐标,利用勾股定理可求出OA的长。
5.【答案】D
【解析】【解答】解:∵点A(m,n)在第三象限,
∴m<0,n<0,
∴m+n<0,
∴点B(0,m+n)在y轴负半轴上.
故选D.
【分析】根据第三象限内点的横坐标与纵坐标都是负数求出m、n都是负数,然后根据坐标轴上点的坐标特征解答.
6.【答案】
【解析】【解答】解:解: 的横坐标相同,纵坐标不同,
与 轴平行,
故答案是: .
【分析】先求出 的横坐标相同,纵坐标不同,再求解即可。
7.【答案】(3,5)
【解析】【解答】解:如图,∵正方形ABCD的边长为4,点A的坐标为(﹣1,1),
∴点C的横坐标为4﹣1=3,
点C的纵坐标为4+1=5,
∴点C的坐标为(3,5).
故答案为:(3,5).
【分析】用正方形的边长加上点A的横坐标得到点C的横坐标,加上点A的纵坐标得到点C的纵坐标,从而得解.
8.【答案】(- 3,2)
【解析】【解答】解:根据坐标系可得点B的坐标为(-3,2)
【分析】根据平面直角坐标系上点B的位置,表示出点B的坐标即可。
9.【答案】(5,1),(1,3),(3,4),(5,5)
【解析】【解答】解:如图所示,C点的坐标为(5,1),(1,3)(3,4),(5,5),
故答案为:(5,1),(1,3),(3,4),(5,5).
【分析】根据三角形面积公式,在第三象限内找出格点C使△ABC的面积为2,然后写出C点坐标.
10.【答案】1或0.2;-3
【解析】【解答】解:(1)根据题意知2x=3x﹣1或﹣2x=3x﹣1,
解得x=1或x=0.2,
故答案为:1或0.2;
(2)根据题意知﹣2x+1﹣3x=16,
解得x=﹣3,
故答案为:﹣3.
【分析】 (1)由点P到两坐标轴的距离相,可得点P的横纵坐标相等或互为相反数,据此解答即可;
(2) 由于点P在第三象限,可得坐标符号为负负,根据点到两坐标轴的距离之和为16, 可得﹣2x+1﹣3x=16,解出x值即可.
11.【答案】解答:由第二象限内的点的横坐标小于零,得a=-3.
由第二象限内点的纵坐标大于零,得b=8,
故P点坐标是(-3,8)
【解析】【分析】根据第二象限内的点的横坐标小于零,可得a的值,根据第二象限内点的纵坐标大于零,可得b的值
12.【答案】解:根据题意得,m-1=3m+5或m-1=-(3m+5),
解m-1=3m+5,得m=-3,
∴m-1=-4,点B的坐标为(-4,-4),
解m-1=-(3m+5),得m=-1,
∴m-1=-2,点B的坐标为(-2,2),
∴点B的坐标为(-4,-4)或(-2,2).
【解析】【分析】根据点B 到x轴的距离与它到y轴的距离相等,坐标平面内的点到两轴的距离实际上就是该点两坐标的绝对值即可得出答案.
13.【答案】解:∵点A(2m﹣n,m+2n)在第四象限,点A到x轴的距离为1,到y轴的距离为8,
∴ ,
解得 ,
∴(m+n)2021=12021=1.
【解析】【分析】据第四象限内点的横坐标是正数,纵坐标是负数,点到x轴的距离等于纵坐标的绝对值,到y轴的距离等于横坐标的绝对值列方程求出m、n的值,再求解即可。
14.【答案】解:(1)∵点A在y轴上,∴3a﹣5=0,解得:a=,a+1=,点A的坐标为:(0,);(2)∵点A到x轴的距离与到y轴的距离相等,∴|3a﹣5|=|a+1|,①3a﹣5=a+1,解得:a=3,则点A(4,4);②3a﹣5=﹣(a+1),解得:a=1,则A(-2,2)
【解析】【分析】(1)根据点在y轴上,横坐标为0,求出a的值,即可解答;
(2)根据点A到x轴的距离与到y轴的距离相等,得到|3a﹣5|=|a+1|,即可解答.
【北师大版】
【同步训练】
一、单选题
1.象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏,如图,若表示棋子“馬”和“車”的点的坐标分别为( , ),(﹣ , ),则表示棋子“炮”的点的坐标为( )
A.(1,2) B.(0,2) C.(2,1) D.(2,0)
2.在平面直角坐标系中,点(﹣2,﹣2m+3)在第三象限,则m的取值范围是( )
A. B. C. D.
3.如图,在平面直角坐标系中,点A的坐标是(﹣3,0),点B的坐标是(0,4),点M是OB上一点,将 ABM沿AM折叠,点B恰好落在x轴上的点 处,则点M的坐标为( )
A.( ,0) B.(0, ) C.( ,0) D.(0, )
4.若点 到y轴的距离是它到x轴距离的两倍,则( ).
A. B. C. D.
5.如图,在平面直角坐标系中,点根据这个规律,探究可得点 , , , ......根据这个规律,探究可得点 的坐标是( ).
A.(2020,0) B.(2020,2)
C.(2020,-2) D.(2021,0)
二、填空题
6.已知点 、 ,点P在 轴上,且 的面积为5,则点P的坐标为 .
7.在平面直角坐标系中,一个长方形三个顶点的坐标为,,,则第四个顶点的坐标为 .
8.已知 轴上一点 , , 为 轴上的一动点,连接 ,以 为边作等边 如图所示,已知点 随着点 的运动形成的图形是一条直线,连接 ,则 的最小值是 .
9.如图,在平面直角坐标系中,一巡查机器人接到指令,从原点O出发,沿O→A1→A2→A3→A4→A5→A6→A7→A8…的路线移动,每次移动1个单位长度,依次得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),A5(2,﹣1),A6(3,﹣1),A7(3,0),A8(4,0),…若机器人巡查到某一位置的横坐标为23时,即停止,则其纵坐标为 .
三、解答题
10.在平面直角坐标系内,已知点Q(m+3,2m+4)在x轴上,求m的值及点Q的坐标?
11.若点 的横纵坐标同号,且点P到两坐标轴的距离相等,求 的平方根,
12.阅读与理解:
如图,一只甲虫在5×5的方格(每个方格边长均为1)上沿着网格线爬行.若我们规定:在如图网格中,向上(或向右)爬行记为“+”,向下(或向左)爬行记为“-”,并且第一个数表示左右方向,第二个数表示上下方向。
例如:从A到B记为:A→B(+1,+4),
从D到C记为:D→C(-1,+2)。
思考与应用:
(1)图中A→C( , );
B→C( , );
D→A( , )。
(2)若甲虫从A到P的行走路线依次为:(+3,+2)→(+1,+3)→(+1,-2),请在图中标出P的位置。
(3)若甲虫的行走路线为A一(+1,+4)→(+2,0)→(+1,-2)-(-4,-2),请计算该甲虫走过的总路程。
13.如图,在平面直角坐标系中,矩形 的边 在 轴上,顶点 , ,连接 ,按下列方法作图:
(1)以点 为圆心,适当长为半径画弧,分别交 、 于点 , ;
(2)分别以点 , 为圆心,大于 的长为半径画弧两弧交于点 ;
(3)作射线 交 于点 ,则点 的横坐标为( )
A.
B.
C.1
D.
【课后作业】
一、单选题
1.若x轴上的点P到y轴的距离为3,则点P的坐标为( )
A.(3,0) B.(3,0)或(–3,0)
C.(0,3) D.(0,3)或(0,–3)
2.在平面直角坐标系中,点,,,若轴,则线段BC的最小值及此时点C的坐标分别为( )
A.3, B.10,
C.1, D.6,
3.对平面上任意一点(a,b),定义f,g两种变换:f(a,b)=(a,﹣b).如f(1,2)=(1,﹣2);g(a,b)=(b,a).如g(1,2)=(2,1).据此得g(f(5,﹣9))=( )
A.(5,﹣9) B.(﹣9,﹣5)
C.(5,9) D.(9,5)
4.已知点A的坐标为(2,-1),则点A到原点的距离为( )
A.3 B. C. D.1
5.如果点A(m,n)在第三象限,那么点B(0,m+n)在 ( )
A.x轴正半轴上 B.x轴负半轴上 C.y轴正半轴上 D.y轴负半轴上
二、填空题
6.若M(4,2),点N(4,5),则直线 与 轴平行.
7.如图,正方形ABCD的边长为4,点A的坐标为(﹣1,1),AB平行于x轴,则点C的坐标为 .
8.如图所示,在平面直角坐标系中,点B的坐标是
9.如图,在直角坐标系中,△ABC的面积为2,三个顶点的坐标分别为A(3,2),B(1,1),C(a,b),且a、b均为正整数,则C点的坐标为 .
10.已知点P(2x,3x﹣1)是平面直角坐标系内的点.
⑴若点P到两坐标轴的距离相等,则x的值是 ;
⑵若点P在第三象限,且到两坐标轴的距离之和为16,则x的值 .
三、解答题
11.已知点P(a,b)在第二象限,且|a|=3,|b|=8,求点P的坐标
12.如果点B 到x轴的距离与它到y轴的距离相等,求点B的坐标.
13.在平面直角坐标系中,点A(2m﹣n,m+2n)在第四象限,点A到x轴的距离为1,到y轴的距离为8,试求(m+n)2021的值.
14.在平面直角坐标系中,点A的坐标是(3a﹣5,a+1)
(1)若点A在y轴上,求a的值及点A的坐标.
(2)若点A到x轴的距离与到y轴的距离相等;求a的值及点A的坐标.
【同步训练答案】
1.【答案】B
【解析】【解答】解:根据棋子“馬”和“車”的点的坐标可建立直角坐标系,如图所示:
故棋子“炮”的点的坐标为:(0,2).
故答案为:B.
【分析】根据题目描述找出x轴、y轴及原点,画出直角坐标系,得出棋子“炮”的点的坐标 .
2.【答案】B
【解析】【解答】解:∵点在第三象限,
∴点的横坐标是负数,纵坐标也是负数,
即﹣2m+3<0,
解得m>.
故选B.
【分析】点在第三象限的条件是:横坐标是负数,纵坐标是负数,可得﹣2m+3<0,求不等式的解即可.
3.【答案】B
【解析】【解答】解:设 ,则 ,
由题意可得: , ,
由勾股定理得: ,
由勾股定理可得: ,即
解得 , ,即
故答案为:B.
【分析】设BM=x,在直角三角形ABO中,用勾股定理可求得AB的值,在直角三角形B OM中,用勾股定理可得关于x的方程,解方程求得x的值,于是OM=OB-BM可求解.
4.【答案】C
【解析】【解答】解:点 到y轴的距离是它到x轴距离的两倍.则 ,
故答案为:C.
【分析】点到x轴的距离为纵坐标的绝对值,到y轴的距离为横坐标的绝对值,据此即可得到m、n的关系.
5.【答案】A
【解析】【解答】通过观察发现,点的横坐标依次是0,1,2,3,……,点的纵坐标为2,0,-2,0四个数一循环,
∵ ,
∴ 的横坐标为2020,纵坐标为0,
∴点 的坐标是(2020,0).
故答案为:A.
【分析】观察点的横纵坐标的特点,找出规律,利用规律即可得出答案.
6.【答案】(-4,0)或(6,0)
【解析】【解答】解:如图,设P(m,0),
由题意: |1-m| 2=5,
∴m=-4或6,
∴P(-4,0)或(6,0),
故答案为:(-4,0)或(6,0)
【分析】设P(m,0),利用三角形的面积公式构建绝对值方程求出m即可;
7.【答案】
【解析】【解答】点和的横坐标相等,
点和的纵坐标相等,
要使这四个点构成矩形,则第四个点的横坐标与相等,纵坐标与相等,
∴第四个顶点的坐标为;
故答案是.
【分析】根据长方形的性质,分析各点坐标之间关系即可求出第四个顶点的坐标。
8.【答案】
【解析】【解答】解:如图,在第四象限以OA为长作等边△AOD,连接OD,并作直线CD延长AD交y轴于点A'
∵等边△ABC,等边△AOD
∴AB=AC,AO=AD,∠BAC=∠OAD=60°
∴∠BAC-∠OAC=∠OAD-∠OAC
∴∠BAO=∠CAD
在△BAO和△CAD中
∴△BAO≌△CAD(SAS)
∴∠AOB=∠ADC
∵∠AOB=90°
∴∠ADC=90°
∴CD⊥AD,
∴点C随着点B的运动形成的图形是直线CD
∵∠AOA'=90°,∠OAD=60°
∴∠AA'O=30°
∴OA=AA'
∴AD=OA=AA'
∴ 点D是AA'的中点,
∴CD垂直平分AA'
∴AC=A'C
∴AC+OC=A'C+OC
∵点C在直线CD上运动,所以点O、C、A'三点共线时,A'C+OC的值最小,最小值为OA'的长
在Rt△AOA'中,∠OAD=60°,OA=1
∴OA'=OAtan60°=
∴AC+OC的最小值为
故答案为:
【分析】 根据题意,在第四象限以OA为边作等边△AOD,连接OD,作直线CD,延长AD交y轴于点A',利用等边三角形的性质,可证得AB=AC,AO=AD,∠BAC=∠OAD,即可证得∠BAO=∠CAD,再利用SAS证明△BAO≌△CAD,利用全等三角形的性质,去证明CD⊥AD,再由点C随着点B的运动形成的图形是直线CD,易证CD垂直平分AA', 利用垂直平分线的性质,可证AC=A'C,点C在直线CD上运动,所以点O、C、A'三点共线时,A'C+OC的值最小,最小值为OA'的长,然后利用解直角三角形求出OA'的长即可求解。
9.【答案】﹣1
【解析】【解答】由题可知,纵坐标从O到A8是一组循环,
23÷9=2…5,
∴横坐标是23时,移动到的位置与点A5的位置相同,
∴纵坐标是﹣1;
故答案为﹣1.
【分析】由图可知:纵坐标从O到A8是一组循环,然后即可算出横坐标是23时,移动到的位置与点A5的位置相同,
10.【答案】解:∵点Q(m+3,2m+4)在x轴上,
∴2m+4=0,
解得m=﹣2,
∴m+3=﹣2+3=1,
∴点Q的坐标为(1,0).
【解析】【分析】根据x轴上点的纵坐标为0列方程求解即可得到m的值,然后求解即可得到点Q的坐标.
11.【答案】解:由题意,得 ,解得 ,
故 ,
的平方根为
【解析】【分析】由题意得1-a=2a+7,解得a=-2,故6-5a=16,所以6-5a的平方根为±4.
12.【答案】(1)+3;+4;+2;0;﹣4;﹣2
(2)解:如图2所示.
(3)解:甲虫走过的总路程:
|+1|+|+4|+|+2|+|+1|+|﹣2|+|﹣4|+|﹣2|=16.
【解析】【分析】(1)根据题意,可依次表示出行走方向。
(2)根据所走的路线,可找出P的位置。
(3)根据行走路线,计算得出总路程。
13.【答案】;A
【解析】【解答】解:过 点作 于 ,如图,
由作法得 平分 ,
,
矩形 的顶点 的坐标为 , 点坐标为 ,
, ,
在 中, ,
在 和 中,
,
∴ ,
,
,
设 ,则 , ,
在 中, ,
解得 ,
即 ,
点的横坐标为 .
故答案为:A.
【分析】过点H作MH⊥AC于点M,利用角平分线的性质可证得MH=HD;利用矩形的性质可求出AB,BC的长,利用勾股定理求出AC的长;再利用HL证明Rt△CHD≌Rt△CHM,由此可求出CM的长;根据AM=AC-CM,可求出AM的长;设DH=t,可表示出AH,HM的长,利用勾股定理建立关于t的方程,解方程求出t的值,即可得到HD的长,由此可得到点H的横坐标.
【课后作业答案】
1.【答案】B
【解析】【分析】根据x轴上的点P到y轴的距离为3,可得点P的横坐标为±3,进而根据x轴上点的纵坐标为0可得具体坐标.
【解答】∵x轴上的点P到y轴的距离为3,
∴点P的横坐标为±3,
∵x轴上点的纵坐标为0,
∴点P的坐标为(3,0)或(-3,0),
故选:B.
【点评】本题考查了点的坐标的相关知识;用到的知识点为:x轴上点的纵坐标为0
2.【答案】A
【解析】【解答】解:依题意可得:
∵AC∥x轴,A(-3,2)
∴y=2,
根据垂线段最短,当BC⊥AC于点C时,
点B到AC的距离最短,即BC的最小值=5-2=3,
此时点C的坐标为(3,2),
故答案为:A.
【分析】根据点坐标的定义及垂线段最短的性质可得答案。
3.【答案】D
【解析】【分析】根据两种变换的规则,先计算f(5,﹣9)=(5,9),再计算g(5,9)即可。
【解答】g(f(5,﹣9))=g(5,9)=(9,5).
故选D.
4.【答案】C
【解析】【解答】解:∵点A的坐标为(2,-1),
∴点A到原点O的距离OA ,
故答案为:C
【分析】由点A的坐标,利用勾股定理可求出OA的长。
5.【答案】D
【解析】【解答】解:∵点A(m,n)在第三象限,
∴m<0,n<0,
∴m+n<0,
∴点B(0,m+n)在y轴负半轴上.
故选D.
【分析】根据第三象限内点的横坐标与纵坐标都是负数求出m、n都是负数,然后根据坐标轴上点的坐标特征解答.
6.【答案】
【解析】【解答】解:解: 的横坐标相同,纵坐标不同,
与 轴平行,
故答案是: .
【分析】先求出 的横坐标相同,纵坐标不同,再求解即可。
7.【答案】(3,5)
【解析】【解答】解:如图,∵正方形ABCD的边长为4,点A的坐标为(﹣1,1),
∴点C的横坐标为4﹣1=3,
点C的纵坐标为4+1=5,
∴点C的坐标为(3,5).
故答案为:(3,5).
【分析】用正方形的边长加上点A的横坐标得到点C的横坐标,加上点A的纵坐标得到点C的纵坐标,从而得解.
8.【答案】(- 3,2)
【解析】【解答】解:根据坐标系可得点B的坐标为(-3,2)
【分析】根据平面直角坐标系上点B的位置,表示出点B的坐标即可。
9.【答案】(5,1),(1,3),(3,4),(5,5)
【解析】【解答】解:如图所示,C点的坐标为(5,1),(1,3)(3,4),(5,5),
故答案为:(5,1),(1,3),(3,4),(5,5).
【分析】根据三角形面积公式,在第三象限内找出格点C使△ABC的面积为2,然后写出C点坐标.
10.【答案】1或0.2;-3
【解析】【解答】解:(1)根据题意知2x=3x﹣1或﹣2x=3x﹣1,
解得x=1或x=0.2,
故答案为:1或0.2;
(2)根据题意知﹣2x+1﹣3x=16,
解得x=﹣3,
故答案为:﹣3.
【分析】 (1)由点P到两坐标轴的距离相,可得点P的横纵坐标相等或互为相反数,据此解答即可;
(2) 由于点P在第三象限,可得坐标符号为负负,根据点到两坐标轴的距离之和为16, 可得﹣2x+1﹣3x=16,解出x值即可.
11.【答案】解答:由第二象限内的点的横坐标小于零,得a=-3.
由第二象限内点的纵坐标大于零,得b=8,
故P点坐标是(-3,8)
【解析】【分析】根据第二象限内的点的横坐标小于零,可得a的值,根据第二象限内点的纵坐标大于零,可得b的值
12.【答案】解:根据题意得,m-1=3m+5或m-1=-(3m+5),
解m-1=3m+5,得m=-3,
∴m-1=-4,点B的坐标为(-4,-4),
解m-1=-(3m+5),得m=-1,
∴m-1=-2,点B的坐标为(-2,2),
∴点B的坐标为(-4,-4)或(-2,2).
【解析】【分析】根据点B 到x轴的距离与它到y轴的距离相等,坐标平面内的点到两轴的距离实际上就是该点两坐标的绝对值即可得出答案.
13.【答案】解:∵点A(2m﹣n,m+2n)在第四象限,点A到x轴的距离为1,到y轴的距离为8,
∴ ,
解得 ,
∴(m+n)2021=12021=1.
【解析】【分析】据第四象限内点的横坐标是正数,纵坐标是负数,点到x轴的距离等于纵坐标的绝对值,到y轴的距离等于横坐标的绝对值列方程求出m、n的值,再求解即可。
14.【答案】解:(1)∵点A在y轴上,∴3a﹣5=0,解得:a=,a+1=,点A的坐标为:(0,);(2)∵点A到x轴的距离与到y轴的距离相等,∴|3a﹣5|=|a+1|,①3a﹣5=a+1,解得:a=3,则点A(4,4);②3a﹣5=﹣(a+1),解得:a=1,则A(-2,2)
【解析】【分析】(1)根据点在y轴上,横坐标为0,求出a的值,即可解答;
(2)根据点A到x轴的距离与到y轴的距离相等,得到|3a﹣5|=|a+1|,即可解答.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
