2022-2023学年北师大版九年级数学上册第4章图形的相似 解答题专题训练 (word版含答案)
文档属性
| 名称 | 2022-2023学年北师大版九年级数学上册第4章图形的相似 解答题专题训练 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 358.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-27 18:37:19 | ||
图片预览


文档简介
2022-2023学年北师大版九年级数学上册《第4章图形的相似》解答题专题训练(附答案)
1.已知a、b、c是△ABC的三边,且满足==,a+b+c=12,试判断△ABC的形状,并说明理由.
2.已知△ABC和△DEF中,有,且△DEF和△ABC的周长之差为15厘米,求△ABC和△DEF的周长.
3.如图,a∥b∥c,直线m,n交于点O,且分别与直线a,b,c交于点A、B、C和点D、E、F,已知OA=1,OB=2,BC=4,EF=5,求DE的长度.
4.如图,已知DE∥BC,FE∥CD,AF=3,AD=5,AE=4.
(1)求CE的长;
(2)求AB的长.
5.如图,在△ABC中,BC的垂直平分线分别交BC,AC于点D,E,BE交AD于点F,AB=AD.
(1)求证:△BFD∽△CAB;
(2)求证:AF=DF;
(3)的值等于 .(直接写出结果,无需解答过程)
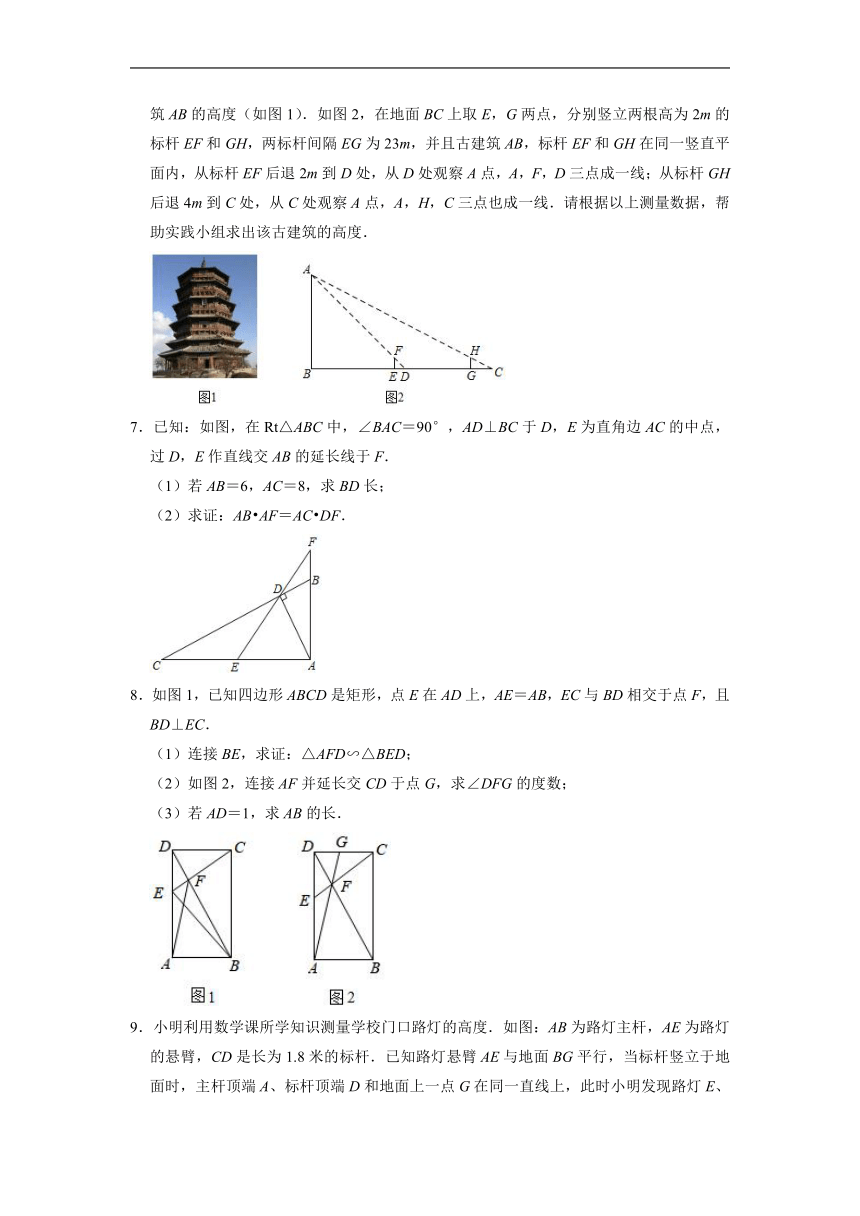
6.学完了《图形的相似》这一章后,某中学数学实践小组决定利用所学知识去测量一古建筑AB的高度(如图1).如图2,在地面BC上取E,G两点,分别竖立两根高为2m的标杆EF和GH,两标杆间隔EG为23m,并且古建筑AB,标杆EF和GH在同一竖直平面内,从标杆EF后退2m到D处,从D处观察A点,A,F,D三点成一线;从标杆GH后退4m到C处,从C处观察A点,A,H,C三点也成一线.请根据以上测量数据,帮助实践小组求出该古建筑的高度.
7.已知:如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于D,E为直角边AC的中点,过D,E作直线交AB的延长线于F.
(1)若AB=6,AC=8,求BD长;
(2)求证:AB AF=AC DF.
8.如图1,已知四边形ABCD是矩形,点E在AD上,AE=AB,EC与BD相交于点F,且BD⊥EC.
(1)连接BE,求证:△AFD∽△BED;
(2)如图2,连接AF并延长交CD于点G,求∠DFG的度数;
(3)若AD=1,求AB的长.
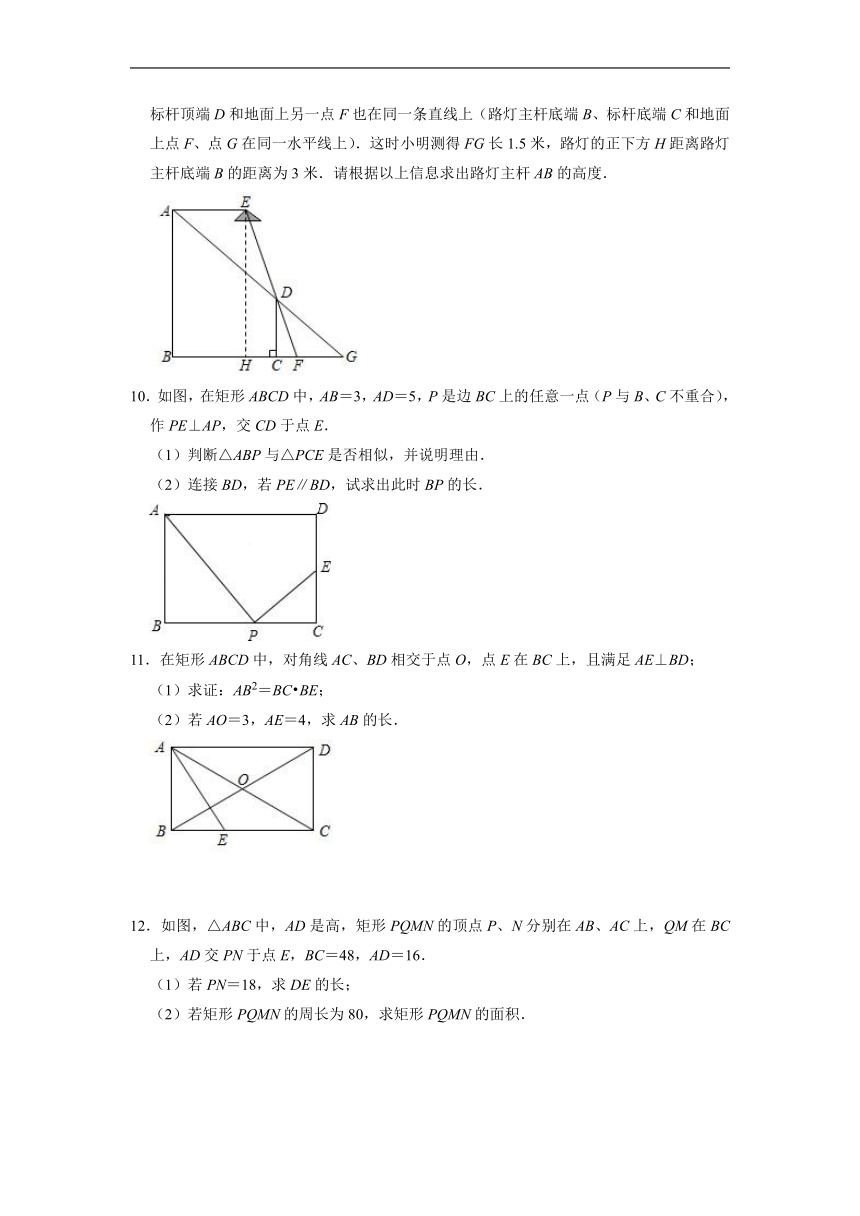
9.小明利用数学课所学知识测量学校门口路灯的高度.如图:AB为路灯主杆,AE为路灯的悬臂,CD是长为1.8米的标杆.已知路灯悬臂AE与地面BG平行,当标杆竖立于地面时,主杆顶端A、标杆顶端D和地面上一点G在同一直线上,此时小明发现路灯E、标杆顶端D和地面上另一点F也在同一条直线上(路灯主杆底端B、标杆底端C和地面上点F、点G在同一水平线上).这时小明测得FG长1.5米,路灯的正下方H距离路灯主杆底端B的距离为3米.请根据以上信息求出路灯主杆AB的高度.
10.如图,在矩形ABCD中,AB=3,AD=5,P是边BC上的任意一点(P与B、C不重合),作PE⊥AP,交CD于点E.
(1)判断△ABP与△PCE是否相似,并说明理由.
(2)连接BD,若PE∥BD,试求出此时BP的长.
11.在矩形ABCD中,对角线AC、BD相交于点O,点E在BC上,且满足AE⊥BD;
(1)求证:AB2=BC BE;
(2)若AO=3,AE=4,求AB的长.
12.如图,△ABC中,AD是高,矩形PQMN的顶点P、N分别在AB、AC上,QM在BC上,AD交PN于点E,BC=48,AD=16.
(1)若PN=18,求DE的长;
(2)若矩形PQMN的周长为80,求矩形PQMN的面积.
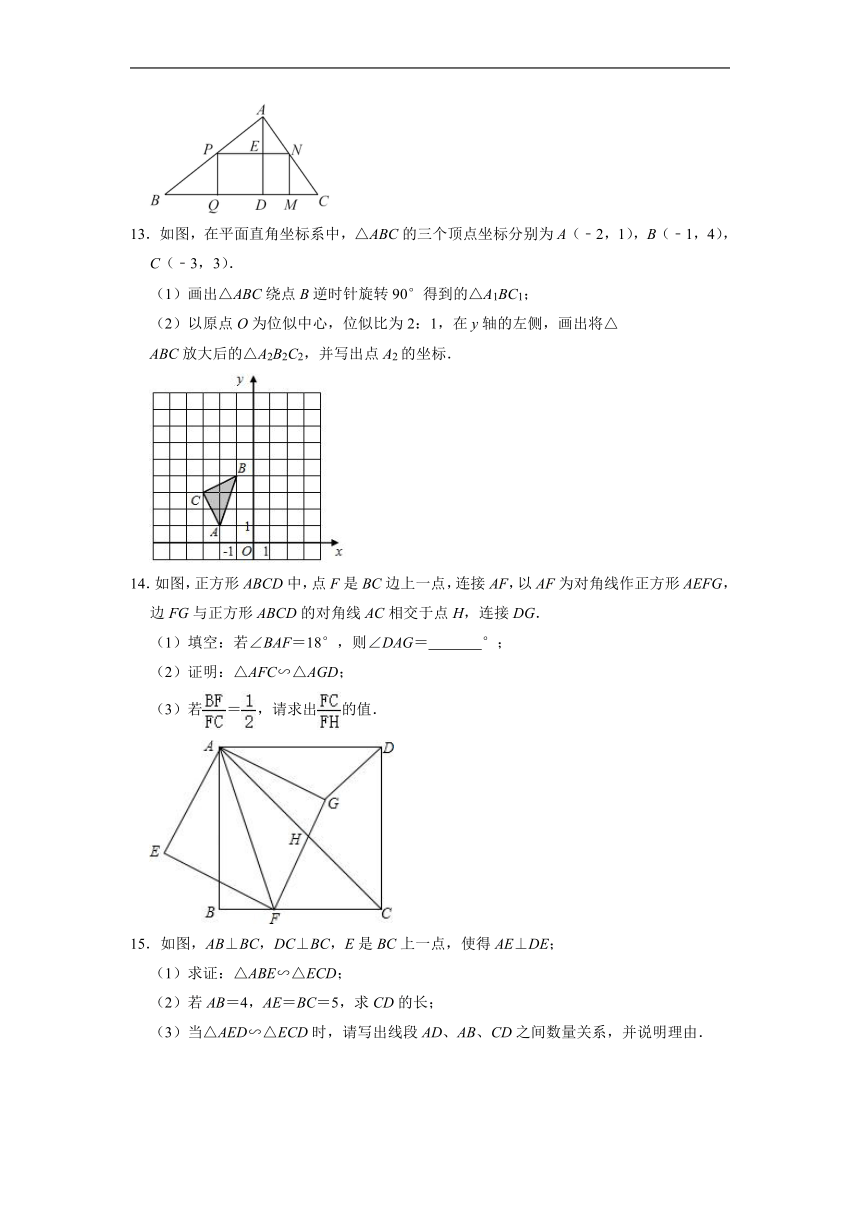
13.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣1,4),C(﹣3,3).
(1)画出△ABC绕点B逆时针旋转90°得到的△A1BC1;
(2)以原点O为位似中心,位似比为2:1,在y轴的左侧,画出将△
ABC放大后的△A2B2C2,并写出点A2的坐标.
14.如图,正方形ABCD中,点F是BC边上一点,连接AF,以AF为对角线作正方形AEFG,边FG与正方形ABCD的对角线AC相交于点H,连接DG.
(1)填空:若∠BAF=18°,则∠DAG= °;
(2)证明:△AFC∽△AGD;
(3)若=,请求出的值.
15.如图,AB⊥BC,DC⊥BC,E是BC上一点,使得AE⊥DE;
(1)求证:△ABE∽△ECD;
(2)若AB=4,AE=BC=5,求CD的长;
(3)当△AED∽△ECD时,请写出线段AD、AB、CD之间数量关系,并说明理由.
16.如图,在平面直角坐标系中,已知OA=12厘米,OB=6厘米,点P从点O开始沿OA边向点A以1厘米/秒的速度移动.点Q从点B开始沿BO边向点O以1厘米/秒的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6),那么,当t为何值时,△POQ与△AOB相似?
17.如图,在正方形ABCD中,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连接DF,交BE的延长线于点G.
(1)求证:△BCE≌△DCF;
(2)求证:BF=BD;
(3)已知AB=2,O是BD的中点,连接OG交CD于点M,求ME的长.
18.已知:如图,在△ABC中,AB=AC,DE∥BC,点F在边AC上,DF与BE相交于点G,且∠EDF=∠ABE.
求证:(1)△DEF∽△BDE;
(2)DG DF=DB EF.
19.如图所示,AD、BC为两路灯,身高相同的小明、小亮站在两路灯杆之间,两人相距6.5m,小明站在P处,小亮站在Q处,小明在路灯BC下的影长为2m,已知小明身高1.8m,路灯BC高9m.小明在路灯BC下的影子顶部恰好位于路灯DA的正下方,小亮在路灯AD下的影子顶部恰好位于路灯BC的正下方.
①计算小亮在路灯AD下的影长;
②计算AD的高.
20.(1)某学校“智慧方园”数学社团遇到这样一个题目:
如图1,在△ABC中,点O在线段BC上,∠BAO=30°,∠OAC=75°,AO=,BO:CO=1:3,求AB的长.
经过社团成员讨论发现,过点B作BD∥AC,交AO的延长线于点D,通过构造△ABD就可以解决问题(如图2).
请回答:∠ADB= °,AB= .
(2)请参考以上解决思路,解决问题:
如图3,在四边形ABCD中,对角线AC与BD相交于点O,AC⊥AD,AO=,∠ABC=∠ACB=75°,BO:OD=1:3,求DC的长.
参考答案
1.解:△ABC是直角三角形,理由是:
设===k,
则a=3k﹣4,b=2k﹣3,c=4k﹣8,
∵a+b+c=12,
∴3k﹣4+2k﹣3+4k﹣8=12,
∴k=3,
∴a=5,b=3,c=4,
∴b2+c2=32+42=25=a2,
∴△ABC是直角三角形.
2.解:设△ABC和△DEF的周长分别是x厘米和y厘米.
∵,
∴==①
由题意可得:y﹣x=15 ②
由①式得x=y③
将③式代入②式得:y﹣y=15,
∴y=45,
将y=45代入③式得:x=30,
答:△ABC和△DEF的周长分别是30厘米和45厘米.
3.解:∵b∥c,
∴,
∴OE=EF=,
∵a∥c,
∴,
∴DO=OF=×(+5)=,
∴DE=DO+OE=+=.
4.解:(1)∵FE∥CD,
∴=,即=,
解得,AC=,
则CE=AC﹣AE=﹣4=;
(2)∵DE∥BC,
∴==,即=,
解得,AB=.
5.(1)证明:∵DE垂直平分BC,
∴BE=CE,
∴∠C=∠EBD,
∵AB=AD,
∴∠FDB=∠ABD,
∴△BFD∽△CAB;
(2)证明:∵DE垂直平分BC,
∴,
∵△BFD∽△CAB,
∴,
∴FD=AB,
∵AB=AD,
∴FD=AD,
∴AF=FD;
(3)解:如图,过点C作CH∥AD,交BE的延长线于点H,
∵DE垂直平分BC,
∴,
∵CH∥AD,
∴∠BDF=∠BCH,∠BFD=∠BHC,
∴△BDF∽△BCH,
∴,
∵AF=FD,
∴,
∵AD∥HC,
∴∠FAE=∠HCE,∠AFE=∠CHE,
∴△AFE∽△CHE,
∴,
∴,
∵,
∴FH=FB,
∴,
故答案为:.
6.解:设BE=ym,由题意可知,
△ABD∽△FED,△ABC∽△HGC,
∴=,=,
∵EF=HG=2,
∴=,
∴=,
解得:y=23(m),
则=,即=,
解得:AB=25(m),
答:该古建筑的高度为25米.
7.解:(1)∵∠BAC=90°,AB=6,AC=8,
∴BC==10,
∵∠BAC=90°,AD⊥BC,
∴∠CAB=∠ADB,
∵∠B=∠B,
∴△CBA∽△ABD,
∴,
∴,
∴BD=3.6;
(2)证明:由(1)知:BD:AD=AB:AC①,
又∵E为AC的中点,AD⊥BC,
∴ED=AE=EC,
∴∠C=∠EDC=∠FAD=∠BDF,
又∵∠F为公共角,
∴△DBF∽△ADF,
∴BD:AD=DF:AF②,
由①②得,AB:AC=DF:AF,
∴AB AF=AC DF.
8.(1)证明:∵四边形ABCD是矩形,BD⊥EC,
∴∠DFE=∠DAB=90°,
∵∠FDE=∠ADB,
∴△FDE∽△ADB,
∴=,
∵∠EDB=∠FDA,
∴△AFD∽△BED;
(2)解:连接BE,
∵△AFD∽△BED,
∴∠DFA=∠DEB,
∴∠BEA=∠BFA,
∵AE=AB,∠DAB=90°,
∴∠BEA=45°,
∴∠BFA=45°,
∴∠DFG=∠BFA=45°;
(3)解:∵四边形ABCD是矩形,
∴AB=CD,∠CDE=∠DAB=90°,
∵BD⊥EC,
∴∠ADB=∠DCE,
∴△CDE∽△DAB,
∴=,
设AB的长为x,则DE=1﹣x,
∴=,
解得x1=,x2=(舍去),
∴AB的长为.
9.解:过点D作DM⊥AB于M,交EH于点N,
∵AE∥BG,AB⊥BG,
∴AE⊥AB,
∵DM⊥AB,
∴AE∥MD∥BG,
∴AM等于△ADE的边AE上的高,
∵AB⊥BG,EH⊥BG,CD⊥BG,
∴AB∥EH∥CD,
∴AE=BH=3米.BM=CD=1.8米,
∵AE∥BG,
∴△ADE∽△GDF,
∴,即,
∴AM=3.6(米),
∴AB=AM+BM=5.4(米),
答:路灯主杆AB的高度为5.4米.
10.解:(1)△ABP与△PCE相似,理由如下:
∵四边形ABCD是矩形,
∴∠B=∠C=90°,
∴∠BAP+∠BPA=90°,
∵PE⊥AP,
∴∠CPE+∠BPA=90°,
∴∠BAP=∠CPE,
∴△ABP∽△PCE;
(2)连接BD,如图所示:
由(1)知△ABP∽△PCE,
∴=,
∴=,
∵PE∥BD,
∴=,
∴=,
∴=,
∵在矩形ABCD中,AB=3,AD=5,
∴CD=AB=3,CB=AD=5,
∴BP==.
11.证明:如图所示:
(1)∵四边形ABCD是矩形,
∴OA=OB=OC,∠ABC=90°,
∴∠OAB=∠OBA,
又∵AE⊥BD,
∴∠AHB=∠EHB=90°,
又∵∠ABC=∠ABH+CBH=90°,
∠EBH+∠BEH=90°,
∴∠BEA=∠ABH,
∴∠CAB=∠AEB,
∴△ABE∽△CBA(AA),
∴,
∴AB2=BC BE;
(2)设AB=2x,由BC=3x,
由证明(1)得△ABE∽△CBA,
∴,
又∵AO=3,AE=4,
∴
∴在Rt△ABC中,由勾股定理得,
∴AB2+BC2=AC2,
∴(2x)2+(3x)2=62
解得:x=,
∴AB=.
12.解:(1)∵四边形PQMN是矩形,
∴PN∥BC,
∴△APN∽△ABC,
∴=,
设DE=x,则AE=16﹣x,
∴=,
解得x=10,
即DE=10;
(2)∵四边形PQMN是矩形,AD是高,
∴四边形PQDE为矩形,
∴DE=PQ,
设DE=PQ=y,则PN==40﹣y,
同理可得,
=,
∴=,
解得y=4,PN=36,
∴矩形PQMN的面积:4×36=144.
13.解:(1)如图,△A1BC1为所作;
(2)如图,△A2B2C2为所作,点A2的坐标(﹣4,2).
14.解:(1)∵四边形ABCD,AEFG是正方形,
∴∠BAC=∠GAF=45°,
∴∠BAF+∠FAC=∠FAC+∠GAC=45°,
∴∠HAG=∠BAF=18°,
∵∠DAG+∠GAH=∠DAC=45°,
∴∠DAG=45°﹣18°=27°,
故答案为:27.
(2)∵四边形ABCD,AEFG是正方形,
∴=,=,
∴=,
∵∠DAG+∠GAC=∠FAC+∠GAC=45°,
∴∠DAG=∠CAF,
∴△AFC∽△AGD;
(3)∵=,
设BF=k,CF=2k,则AB=BC=3k,
∴AF===k,AC=AB=3k,
∵四边形ABCD,AEFG是正方形,
∴∠AFH=∠ACF,∠FAH=∠CAF,
∴△AFH∽△ACF,
∴=,
∴==.
15.(1)证明:∵AB⊥BC,DC⊥BC,
∴∠B=∠C=90°,∠BAE+∠AEB=90°,
∵AE⊥DE,
∴∠AED=90°,
∴∠AEB+∠DEC=90°,
∴∠DEC=∠BAE,
∴△ABE∽△ECD;
(2)解:Rt△ABE中,∵AB=4,AE=5,
∴BE=3,
∵BC=5,
∴EC=5﹣3=2,
由(1)得:△ABE∽△ECD,
∴,
∴,
∴CD=;
(3)解:线段AD、AB、CD之间数量关系:AD=AB+CD;
理由是:过E作EF⊥AD于F,
∵△AED∽△ECD,
∴∠EAD=∠DEC,
∵∠AED=∠C,
∴∠ADE=∠EDC,
∵DC⊥BC,
∴EF=EC,
∵DE=DE,
∴Rt△DFE≌Rt△DCE(HL),
∴DF=DC,
同理可得:△ABE≌△AFE,
∴AF=AB,
∴AD=AF+DF=AB+CD.
16.解:①若△POQ∽△AOB时,=,即=,
整理得:12﹣2t=t,
解得:t=4.
②若△POQ∽△BOA时,=,即=,
整理得:6﹣t=2t,
解得:t=2.
∵0≤t≤6,
∴t=4和t=2均符合题意,
∴当t=4或t=2时,△POQ与△AOB相似.
17.(1)证明:∵四边形ABCD为正方形,
∴BC=DC,∠BCD=90°,
在△BCE和△DCF中
,
∴△BCE≌△DCF(SAS);
(2)∵△BCE≌△DCF,
∴∠CBE=∠CDF,
∵∠CBF+∠CEB=90°,
而∠CEB=∠DEG,
∴∠CDF+∠DEG=90°,
∴∠DGE=90°,即BG⊥DF,
∵BE平分∠DBC,
∴△BDF为等腰三角形,
∴BD=BF;
(3)∵AB=2,
∴BD=2,
∴BF=2,
∵O是BD的中点,BG垂直平分DF,
∴OG为△DBF的中位线,OM为△DCF的中位线,
∴OG=BF=,OM=BC=1,
∴MG=OG﹣OM=﹣1,
∵MG∥BC,
∴△MGE∽△CBE,
∴MG:BC=ME:EC,即(﹣1):2=ME:EC,
∴EC=ME=2(+1)ME,
∵MC=ME+EC=1,
∴ME+2(+1)ME=1,
∴ME=3﹣2.
18.证明:(1)∵AB=AC,
∴∠ABC=∠ACB.
∵DE∥BC,
∴∠ABC+∠BDE=180°,∠ACB+∠CED=180°.
∴∠BDE=∠CED.
∵∠EDF=∠ABE,
∴△DEF∽△BDE.
(2)由△DEF∽△BDE,得.
∴DE2=DB EF.
由△DEF∽△BDE,得∠BED=∠DFE.
∵∠GDE=∠EDF,
∴△GDE∽△EDF.
∴.
∴DE2=DG DF.
∴DG DF=DB EF.
19.解:①∵EP⊥AB,CB⊥AB,
∴∠EPA=∠CBA=90°
∵∠EAP=∠CAB,
∴△EAP∽△CAB
∴
∴
∴AB=10
BQ=10﹣2﹣6.5=1.5;
②∵FQ⊥AB,DA⊥AB,
∴∠FQB=∠DAB=90°
∵∠FBQ=∠DBA,
∴△BFQ∽△BDA
∴=
∴
∴DA=12.
20.解:(1)∵BD∥AC,
∴∠ADB=∠OAC=75°.
∵∠BOD=∠COA,
∴△BOD∽△COA,
∴==.
又∵AO=,
∴OD=AO=,
∴AD=AO+OD=4.
∵∠BAD=30°,∠ADB=75°,
∴∠ABD=180°﹣∠BAD﹣∠ADB=75°=∠ADB,
∴AB=AD=4.
故答案为:75;4.
(2)过点B作BE∥AD交AC于点E,如图所示.
∵AC⊥AD,BE∥AD,
∴∠DAC=∠BEA=90°.
∵∠AOD=∠EOB,
∴△AOD∽△EOB,
∴==.
∵BO:OD=1:3,
∴==.
∵AO=3,
∴EO=,
∴AE=4.
∵∠ABC=∠ACB=75°,
∴∠BAC=30°,AB=AC,
∴AB=2BE.
在Rt△AEB中,BE2+AE2=AB2,即(4)2+BE2=(2BE)2,
解得:BE=4,
∴AB=AC=8,AD=12.
在Rt△CAD中,AC2+AD2=CD2,即82+122=CD2,
解得:CD=4.
1.已知a、b、c是△ABC的三边,且满足==,a+b+c=12,试判断△ABC的形状,并说明理由.
2.已知△ABC和△DEF中,有,且△DEF和△ABC的周长之差为15厘米,求△ABC和△DEF的周长.
3.如图,a∥b∥c,直线m,n交于点O,且分别与直线a,b,c交于点A、B、C和点D、E、F,已知OA=1,OB=2,BC=4,EF=5,求DE的长度.
4.如图,已知DE∥BC,FE∥CD,AF=3,AD=5,AE=4.
(1)求CE的长;
(2)求AB的长.
5.如图,在△ABC中,BC的垂直平分线分别交BC,AC于点D,E,BE交AD于点F,AB=AD.
(1)求证:△BFD∽△CAB;
(2)求证:AF=DF;
(3)的值等于 .(直接写出结果,无需解答过程)
6.学完了《图形的相似》这一章后,某中学数学实践小组决定利用所学知识去测量一古建筑AB的高度(如图1).如图2,在地面BC上取E,G两点,分别竖立两根高为2m的标杆EF和GH,两标杆间隔EG为23m,并且古建筑AB,标杆EF和GH在同一竖直平面内,从标杆EF后退2m到D处,从D处观察A点,A,F,D三点成一线;从标杆GH后退4m到C处,从C处观察A点,A,H,C三点也成一线.请根据以上测量数据,帮助实践小组求出该古建筑的高度.
7.已知:如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于D,E为直角边AC的中点,过D,E作直线交AB的延长线于F.
(1)若AB=6,AC=8,求BD长;
(2)求证:AB AF=AC DF.
8.如图1,已知四边形ABCD是矩形,点E在AD上,AE=AB,EC与BD相交于点F,且BD⊥EC.
(1)连接BE,求证:△AFD∽△BED;
(2)如图2,连接AF并延长交CD于点G,求∠DFG的度数;
(3)若AD=1,求AB的长.
9.小明利用数学课所学知识测量学校门口路灯的高度.如图:AB为路灯主杆,AE为路灯的悬臂,CD是长为1.8米的标杆.已知路灯悬臂AE与地面BG平行,当标杆竖立于地面时,主杆顶端A、标杆顶端D和地面上一点G在同一直线上,此时小明发现路灯E、标杆顶端D和地面上另一点F也在同一条直线上(路灯主杆底端B、标杆底端C和地面上点F、点G在同一水平线上).这时小明测得FG长1.5米,路灯的正下方H距离路灯主杆底端B的距离为3米.请根据以上信息求出路灯主杆AB的高度.
10.如图,在矩形ABCD中,AB=3,AD=5,P是边BC上的任意一点(P与B、C不重合),作PE⊥AP,交CD于点E.
(1)判断△ABP与△PCE是否相似,并说明理由.
(2)连接BD,若PE∥BD,试求出此时BP的长.
11.在矩形ABCD中,对角线AC、BD相交于点O,点E在BC上,且满足AE⊥BD;
(1)求证:AB2=BC BE;
(2)若AO=3,AE=4,求AB的长.
12.如图,△ABC中,AD是高,矩形PQMN的顶点P、N分别在AB、AC上,QM在BC上,AD交PN于点E,BC=48,AD=16.
(1)若PN=18,求DE的长;
(2)若矩形PQMN的周长为80,求矩形PQMN的面积.
13.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣1,4),C(﹣3,3).
(1)画出△ABC绕点B逆时针旋转90°得到的△A1BC1;
(2)以原点O为位似中心,位似比为2:1,在y轴的左侧,画出将△
ABC放大后的△A2B2C2,并写出点A2的坐标.
14.如图,正方形ABCD中,点F是BC边上一点,连接AF,以AF为对角线作正方形AEFG,边FG与正方形ABCD的对角线AC相交于点H,连接DG.
(1)填空:若∠BAF=18°,则∠DAG= °;
(2)证明:△AFC∽△AGD;
(3)若=,请求出的值.
15.如图,AB⊥BC,DC⊥BC,E是BC上一点,使得AE⊥DE;
(1)求证:△ABE∽△ECD;
(2)若AB=4,AE=BC=5,求CD的长;
(3)当△AED∽△ECD时,请写出线段AD、AB、CD之间数量关系,并说明理由.
16.如图,在平面直角坐标系中,已知OA=12厘米,OB=6厘米,点P从点O开始沿OA边向点A以1厘米/秒的速度移动.点Q从点B开始沿BO边向点O以1厘米/秒的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6),那么,当t为何值时,△POQ与△AOB相似?
17.如图,在正方形ABCD中,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连接DF,交BE的延长线于点G.
(1)求证:△BCE≌△DCF;
(2)求证:BF=BD;
(3)已知AB=2,O是BD的中点,连接OG交CD于点M,求ME的长.
18.已知:如图,在△ABC中,AB=AC,DE∥BC,点F在边AC上,DF与BE相交于点G,且∠EDF=∠ABE.
求证:(1)△DEF∽△BDE;
(2)DG DF=DB EF.
19.如图所示,AD、BC为两路灯,身高相同的小明、小亮站在两路灯杆之间,两人相距6.5m,小明站在P处,小亮站在Q处,小明在路灯BC下的影长为2m,已知小明身高1.8m,路灯BC高9m.小明在路灯BC下的影子顶部恰好位于路灯DA的正下方,小亮在路灯AD下的影子顶部恰好位于路灯BC的正下方.
①计算小亮在路灯AD下的影长;
②计算AD的高.
20.(1)某学校“智慧方园”数学社团遇到这样一个题目:
如图1,在△ABC中,点O在线段BC上,∠BAO=30°,∠OAC=75°,AO=,BO:CO=1:3,求AB的长.
经过社团成员讨论发现,过点B作BD∥AC,交AO的延长线于点D,通过构造△ABD就可以解决问题(如图2).
请回答:∠ADB= °,AB= .
(2)请参考以上解决思路,解决问题:
如图3,在四边形ABCD中,对角线AC与BD相交于点O,AC⊥AD,AO=,∠ABC=∠ACB=75°,BO:OD=1:3,求DC的长.
参考答案
1.解:△ABC是直角三角形,理由是:
设===k,
则a=3k﹣4,b=2k﹣3,c=4k﹣8,
∵a+b+c=12,
∴3k﹣4+2k﹣3+4k﹣8=12,
∴k=3,
∴a=5,b=3,c=4,
∴b2+c2=32+42=25=a2,
∴△ABC是直角三角形.
2.解:设△ABC和△DEF的周长分别是x厘米和y厘米.
∵,
∴==①
由题意可得:y﹣x=15 ②
由①式得x=y③
将③式代入②式得:y﹣y=15,
∴y=45,
将y=45代入③式得:x=30,
答:△ABC和△DEF的周长分别是30厘米和45厘米.
3.解:∵b∥c,
∴,
∴OE=EF=,
∵a∥c,
∴,
∴DO=OF=×(+5)=,
∴DE=DO+OE=+=.
4.解:(1)∵FE∥CD,
∴=,即=,
解得,AC=,
则CE=AC﹣AE=﹣4=;
(2)∵DE∥BC,
∴==,即=,
解得,AB=.
5.(1)证明:∵DE垂直平分BC,
∴BE=CE,
∴∠C=∠EBD,
∵AB=AD,
∴∠FDB=∠ABD,
∴△BFD∽△CAB;
(2)证明:∵DE垂直平分BC,
∴,
∵△BFD∽△CAB,
∴,
∴FD=AB,
∵AB=AD,
∴FD=AD,
∴AF=FD;
(3)解:如图,过点C作CH∥AD,交BE的延长线于点H,
∵DE垂直平分BC,
∴,
∵CH∥AD,
∴∠BDF=∠BCH,∠BFD=∠BHC,
∴△BDF∽△BCH,
∴,
∵AF=FD,
∴,
∵AD∥HC,
∴∠FAE=∠HCE,∠AFE=∠CHE,
∴△AFE∽△CHE,
∴,
∴,
∵,
∴FH=FB,
∴,
故答案为:.
6.解:设BE=ym,由题意可知,
△ABD∽△FED,△ABC∽△HGC,
∴=,=,
∵EF=HG=2,
∴=,
∴=,
解得:y=23(m),
则=,即=,
解得:AB=25(m),
答:该古建筑的高度为25米.
7.解:(1)∵∠BAC=90°,AB=6,AC=8,
∴BC==10,
∵∠BAC=90°,AD⊥BC,
∴∠CAB=∠ADB,
∵∠B=∠B,
∴△CBA∽△ABD,
∴,
∴,
∴BD=3.6;
(2)证明:由(1)知:BD:AD=AB:AC①,
又∵E为AC的中点,AD⊥BC,
∴ED=AE=EC,
∴∠C=∠EDC=∠FAD=∠BDF,
又∵∠F为公共角,
∴△DBF∽△ADF,
∴BD:AD=DF:AF②,
由①②得,AB:AC=DF:AF,
∴AB AF=AC DF.
8.(1)证明:∵四边形ABCD是矩形,BD⊥EC,
∴∠DFE=∠DAB=90°,
∵∠FDE=∠ADB,
∴△FDE∽△ADB,
∴=,
∵∠EDB=∠FDA,
∴△AFD∽△BED;
(2)解:连接BE,
∵△AFD∽△BED,
∴∠DFA=∠DEB,
∴∠BEA=∠BFA,
∵AE=AB,∠DAB=90°,
∴∠BEA=45°,
∴∠BFA=45°,
∴∠DFG=∠BFA=45°;
(3)解:∵四边形ABCD是矩形,
∴AB=CD,∠CDE=∠DAB=90°,
∵BD⊥EC,
∴∠ADB=∠DCE,
∴△CDE∽△DAB,
∴=,
设AB的长为x,则DE=1﹣x,
∴=,
解得x1=,x2=(舍去),
∴AB的长为.
9.解:过点D作DM⊥AB于M,交EH于点N,
∵AE∥BG,AB⊥BG,
∴AE⊥AB,
∵DM⊥AB,
∴AE∥MD∥BG,
∴AM等于△ADE的边AE上的高,
∵AB⊥BG,EH⊥BG,CD⊥BG,
∴AB∥EH∥CD,
∴AE=BH=3米.BM=CD=1.8米,
∵AE∥BG,
∴△ADE∽△GDF,
∴,即,
∴AM=3.6(米),
∴AB=AM+BM=5.4(米),
答:路灯主杆AB的高度为5.4米.
10.解:(1)△ABP与△PCE相似,理由如下:
∵四边形ABCD是矩形,
∴∠B=∠C=90°,
∴∠BAP+∠BPA=90°,
∵PE⊥AP,
∴∠CPE+∠BPA=90°,
∴∠BAP=∠CPE,
∴△ABP∽△PCE;
(2)连接BD,如图所示:
由(1)知△ABP∽△PCE,
∴=,
∴=,
∵PE∥BD,
∴=,
∴=,
∴=,
∵在矩形ABCD中,AB=3,AD=5,
∴CD=AB=3,CB=AD=5,
∴BP==.
11.证明:如图所示:
(1)∵四边形ABCD是矩形,
∴OA=OB=OC,∠ABC=90°,
∴∠OAB=∠OBA,
又∵AE⊥BD,
∴∠AHB=∠EHB=90°,
又∵∠ABC=∠ABH+CBH=90°,
∠EBH+∠BEH=90°,
∴∠BEA=∠ABH,
∴∠CAB=∠AEB,
∴△ABE∽△CBA(AA),
∴,
∴AB2=BC BE;
(2)设AB=2x,由BC=3x,
由证明(1)得△ABE∽△CBA,
∴,
又∵AO=3,AE=4,
∴
∴在Rt△ABC中,由勾股定理得,
∴AB2+BC2=AC2,
∴(2x)2+(3x)2=62
解得:x=,
∴AB=.
12.解:(1)∵四边形PQMN是矩形,
∴PN∥BC,
∴△APN∽△ABC,
∴=,
设DE=x,则AE=16﹣x,
∴=,
解得x=10,
即DE=10;
(2)∵四边形PQMN是矩形,AD是高,
∴四边形PQDE为矩形,
∴DE=PQ,
设DE=PQ=y,则PN==40﹣y,
同理可得,
=,
∴=,
解得y=4,PN=36,
∴矩形PQMN的面积:4×36=144.
13.解:(1)如图,△A1BC1为所作;
(2)如图,△A2B2C2为所作,点A2的坐标(﹣4,2).
14.解:(1)∵四边形ABCD,AEFG是正方形,
∴∠BAC=∠GAF=45°,
∴∠BAF+∠FAC=∠FAC+∠GAC=45°,
∴∠HAG=∠BAF=18°,
∵∠DAG+∠GAH=∠DAC=45°,
∴∠DAG=45°﹣18°=27°,
故答案为:27.
(2)∵四边形ABCD,AEFG是正方形,
∴=,=,
∴=,
∵∠DAG+∠GAC=∠FAC+∠GAC=45°,
∴∠DAG=∠CAF,
∴△AFC∽△AGD;
(3)∵=,
设BF=k,CF=2k,则AB=BC=3k,
∴AF===k,AC=AB=3k,
∵四边形ABCD,AEFG是正方形,
∴∠AFH=∠ACF,∠FAH=∠CAF,
∴△AFH∽△ACF,
∴=,
∴==.
15.(1)证明:∵AB⊥BC,DC⊥BC,
∴∠B=∠C=90°,∠BAE+∠AEB=90°,
∵AE⊥DE,
∴∠AED=90°,
∴∠AEB+∠DEC=90°,
∴∠DEC=∠BAE,
∴△ABE∽△ECD;
(2)解:Rt△ABE中,∵AB=4,AE=5,
∴BE=3,
∵BC=5,
∴EC=5﹣3=2,
由(1)得:△ABE∽△ECD,
∴,
∴,
∴CD=;
(3)解:线段AD、AB、CD之间数量关系:AD=AB+CD;
理由是:过E作EF⊥AD于F,
∵△AED∽△ECD,
∴∠EAD=∠DEC,
∵∠AED=∠C,
∴∠ADE=∠EDC,
∵DC⊥BC,
∴EF=EC,
∵DE=DE,
∴Rt△DFE≌Rt△DCE(HL),
∴DF=DC,
同理可得:△ABE≌△AFE,
∴AF=AB,
∴AD=AF+DF=AB+CD.
16.解:①若△POQ∽△AOB时,=,即=,
整理得:12﹣2t=t,
解得:t=4.
②若△POQ∽△BOA时,=,即=,
整理得:6﹣t=2t,
解得:t=2.
∵0≤t≤6,
∴t=4和t=2均符合题意,
∴当t=4或t=2时,△POQ与△AOB相似.
17.(1)证明:∵四边形ABCD为正方形,
∴BC=DC,∠BCD=90°,
在△BCE和△DCF中
,
∴△BCE≌△DCF(SAS);
(2)∵△BCE≌△DCF,
∴∠CBE=∠CDF,
∵∠CBF+∠CEB=90°,
而∠CEB=∠DEG,
∴∠CDF+∠DEG=90°,
∴∠DGE=90°,即BG⊥DF,
∵BE平分∠DBC,
∴△BDF为等腰三角形,
∴BD=BF;
(3)∵AB=2,
∴BD=2,
∴BF=2,
∵O是BD的中点,BG垂直平分DF,
∴OG为△DBF的中位线,OM为△DCF的中位线,
∴OG=BF=,OM=BC=1,
∴MG=OG﹣OM=﹣1,
∵MG∥BC,
∴△MGE∽△CBE,
∴MG:BC=ME:EC,即(﹣1):2=ME:EC,
∴EC=ME=2(+1)ME,
∵MC=ME+EC=1,
∴ME+2(+1)ME=1,
∴ME=3﹣2.
18.证明:(1)∵AB=AC,
∴∠ABC=∠ACB.
∵DE∥BC,
∴∠ABC+∠BDE=180°,∠ACB+∠CED=180°.
∴∠BDE=∠CED.
∵∠EDF=∠ABE,
∴△DEF∽△BDE.
(2)由△DEF∽△BDE,得.
∴DE2=DB EF.
由△DEF∽△BDE,得∠BED=∠DFE.
∵∠GDE=∠EDF,
∴△GDE∽△EDF.
∴.
∴DE2=DG DF.
∴DG DF=DB EF.
19.解:①∵EP⊥AB,CB⊥AB,
∴∠EPA=∠CBA=90°
∵∠EAP=∠CAB,
∴△EAP∽△CAB
∴
∴
∴AB=10
BQ=10﹣2﹣6.5=1.5;
②∵FQ⊥AB,DA⊥AB,
∴∠FQB=∠DAB=90°
∵∠FBQ=∠DBA,
∴△BFQ∽△BDA
∴=
∴
∴DA=12.
20.解:(1)∵BD∥AC,
∴∠ADB=∠OAC=75°.
∵∠BOD=∠COA,
∴△BOD∽△COA,
∴==.
又∵AO=,
∴OD=AO=,
∴AD=AO+OD=4.
∵∠BAD=30°,∠ADB=75°,
∴∠ABD=180°﹣∠BAD﹣∠ADB=75°=∠ADB,
∴AB=AD=4.
故答案为:75;4.
(2)过点B作BE∥AD交AC于点E,如图所示.
∵AC⊥AD,BE∥AD,
∴∠DAC=∠BEA=90°.
∵∠AOD=∠EOB,
∴△AOD∽△EOB,
∴==.
∵BO:OD=1:3,
∴==.
∵AO=3,
∴EO=,
∴AE=4.
∵∠ABC=∠ACB=75°,
∴∠BAC=30°,AB=AC,
∴AB=2BE.
在Rt△AEB中,BE2+AE2=AB2,即(4)2+BE2=(2BE)2,
解得:BE=4,
∴AB=AC=8,AD=12.
在Rt△CAD中,AC2+AD2=CD2,即82+122=CD2,
解得:CD=4.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
