数学人教A版(2019)选择性必修第一册1.1.2 空间向量的数量积运算 课件(共15张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册1.1.2 空间向量的数量积运算 课件(共15张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 576.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-24 07:49:06 | ||
图片预览





文档简介
(共15张PPT)
1.1.2 空间向量的数量积运算
学习目标
01
掌握空间向量的数量积运算
02
能运用向量的数量积判断两向量的垂直关系
BUSINESS REPORT SUMMARY
新课引入:
1.空间向量的夹角
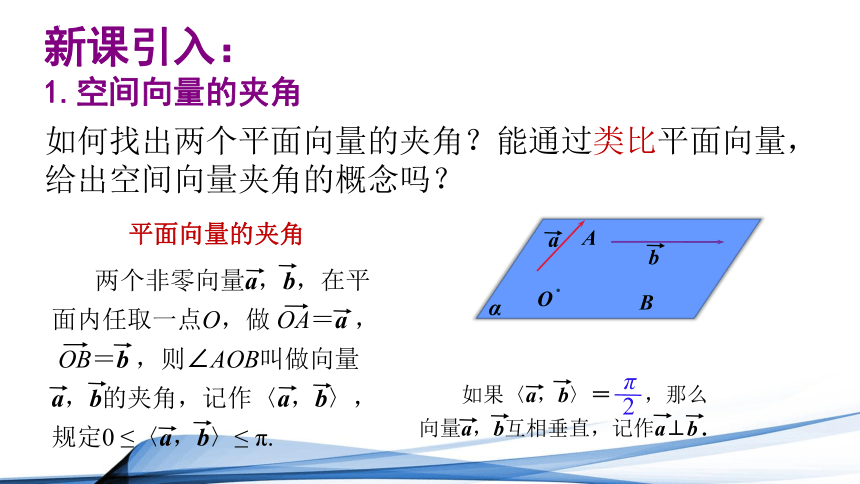
如何找出两个平面向量的夹角?能通过类比平面向量,给出空间向量夹角的概念吗?
平面向量的夹角
两个非零向量a,b,在平面内任取一点O,做 OA=a ,
OB=b ,则∠AOB叫做向量
a,b的夹角,记作〈a,b〉,规定0 ≤〈a,b〉≤ π.
如果〈a,b〉= ,那么向量a,b互相垂直,记作a⊥b .
π
2
.
O
α
A
B
a
b
新课引入:
1.空间向量的夹角
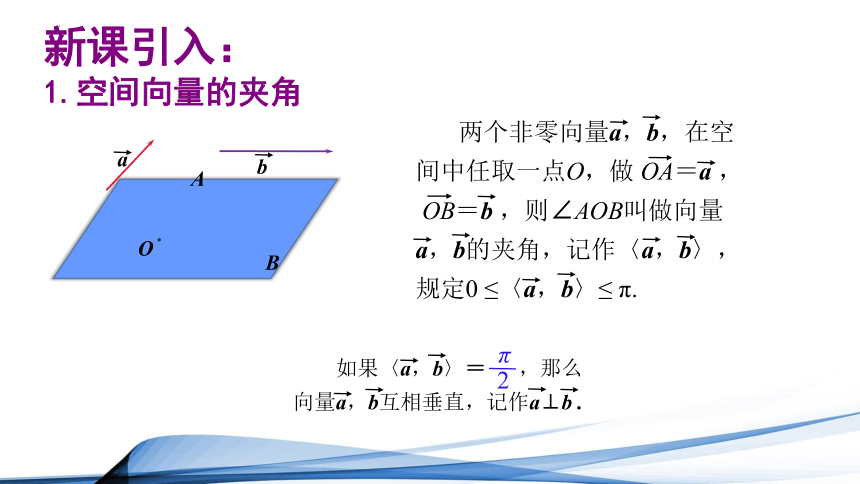
由于任意两个空间向量都可以通过平移转化为同一平面内的向量,因此,两个空间向量的夹角就可以像平面向量那样来定义.
a
b
.
O
A
B
两个非零向量a,b,在空间中任取一点O,做 OA=a ,
OB=b ,则∠AOB叫做向量
a,b的夹角,记作〈a,b〉,规定0 ≤〈a,b〉≤ π.
如果〈a,b〉= ,那么向量a,b互相垂直,记作a⊥b .
π
2
新课引入:
1.空间向量的夹角
新课引入:
2.空间向量的数量积
(1)定义:已知两个非零向量a,b,则|a||b|cos〈a,b〉叫做a,b的数量积,记作a·b.即a·b=|a||b|cos〈a,b〉.
(2)数量积的运算律
(λa)·b=_______,λ∈R
a·b=____
(a+b)·c=_________
λ(a·b)
b·a
a·c+b·c
(交换律)
(分配律)
(3)数量积的性质:
①若a,b是非零向量,则a⊥b _______
②若a与b同向,则a·b=______;若反向,则a·b=________.
③特别地,a·a=____
④若〈a,b〉为a,b的夹角,则cos〈a,b〉=_______
⑤|a·b|≤|a|·|b|
a·b=0
|a|·|b|
-|a|·|b|
|a|2
在平面向量的学习中,我们学习了向量的投影.类似地,在空间,向量a向向量b的投影有什么意义?向量a向直线l的投影呢?向量a向平面β的投影呢?
思考:
3.投影向量
(1)向量a在向量b上的投影
先将向量a与向量b平移到同一平面α内,如图①向量c称为向量a在向量b上的投影向量.
α
b
a
a
(2)向量a在直线l上的投影
如图②向量c称为向量a在直线l上的投影.
α
a
a
c
l
(3)向量a在平面β上的投影
如图③分别由向量a的起点A和终点B作平面β的垂线,垂足分别为A′,B′,则向量A′B′(a′)称为向量a在平面β上的投影向量.
β
a
a
A
B
A′
a′
B′
4.直线与平面所成的角
β
a
a
A
B
A′
a′
B′
如图向量a与向量a′的夹角就是向量a所在直线与平面β所成的角.
例题讲解:
1.空间向量数量积的运算
2.利用空间向量数量积求向量模长
练一练:
1.已知a=3p-2g,b=p+q,p和g是空间中相互垂直的单位向量,则a·b=
A.1 B.2 C.3 D.4
2.(2022福建三明一中开学考试)在三棱锥A-BCD
中,AB=AC=AD=2,BAD=90°,LBAC=60°.则AB·CD等于( )
A.-2 B.2 C.-2/3 D.2/3
3.已知lal=4, lbl=8,a与b的夹角是120°,
当a+2b与ka-b的夹角为钝角时,k的取值范围为
3.利用空间向量数量积求向量夹角
4.(2021天津西青期末)如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,P是C1D1的中点,则B1C·A1P=
,B1C与A1P所成角的大小为
4.利用空间向量数量积判断或证明垂直问题
例3 如图1.1-13,m,n是平面a内的两条相交直线.如果l垂直m,l垂直n,
求证:l垂直a.
THANKS
1.1.2 空间向量的数量积运算
学习目标
01
掌握空间向量的数量积运算
02
能运用向量的数量积判断两向量的垂直关系
BUSINESS REPORT SUMMARY
新课引入:
1.空间向量的夹角
如何找出两个平面向量的夹角?能通过类比平面向量,给出空间向量夹角的概念吗?
平面向量的夹角
两个非零向量a,b,在平面内任取一点O,做 OA=a ,
OB=b ,则∠AOB叫做向量
a,b的夹角,记作〈a,b〉,规定0 ≤〈a,b〉≤ π.
如果〈a,b〉= ,那么向量a,b互相垂直,记作a⊥b .
π
2
.
O
α
A
B
a
b
新课引入:
1.空间向量的夹角
由于任意两个空间向量都可以通过平移转化为同一平面内的向量,因此,两个空间向量的夹角就可以像平面向量那样来定义.
a
b
.
O
A
B
两个非零向量a,b,在空间中任取一点O,做 OA=a ,
OB=b ,则∠AOB叫做向量
a,b的夹角,记作〈a,b〉,规定0 ≤〈a,b〉≤ π.
如果〈a,b〉= ,那么向量a,b互相垂直,记作a⊥b .
π
2
新课引入:
1.空间向量的夹角
新课引入:
2.空间向量的数量积
(1)定义:已知两个非零向量a,b,则|a||b|cos〈a,b〉叫做a,b的数量积,记作a·b.即a·b=|a||b|cos〈a,b〉.
(2)数量积的运算律
(λa)·b=_______,λ∈R
a·b=____
(a+b)·c=_________
λ(a·b)
b·a
a·c+b·c
(交换律)
(分配律)
(3)数量积的性质:
①若a,b是非零向量,则a⊥b _______
②若a与b同向,则a·b=______;若反向,则a·b=________.
③特别地,a·a=____
④若〈a,b〉为a,b的夹角,则cos〈a,b〉=_______
⑤|a·b|≤|a|·|b|
a·b=0
|a|·|b|
-|a|·|b|
|a|2
在平面向量的学习中,我们学习了向量的投影.类似地,在空间,向量a向向量b的投影有什么意义?向量a向直线l的投影呢?向量a向平面β的投影呢?
思考:
3.投影向量
(1)向量a在向量b上的投影
先将向量a与向量b平移到同一平面α内,如图①向量c称为向量a在向量b上的投影向量.
α
b
a
a
(2)向量a在直线l上的投影
如图②向量c称为向量a在直线l上的投影.
α
a
a
c
l
(3)向量a在平面β上的投影
如图③分别由向量a的起点A和终点B作平面β的垂线,垂足分别为A′,B′,则向量A′B′(a′)称为向量a在平面β上的投影向量.
β
a
a
A
B
A′
a′
B′
4.直线与平面所成的角
β
a
a
A
B
A′
a′
B′
如图向量a与向量a′的夹角就是向量a所在直线与平面β所成的角.
例题讲解:
1.空间向量数量积的运算
2.利用空间向量数量积求向量模长
练一练:
1.已知a=3p-2g,b=p+q,p和g是空间中相互垂直的单位向量,则a·b=
A.1 B.2 C.3 D.4
2.(2022福建三明一中开学考试)在三棱锥A-BCD
中,AB=AC=AD=2,BAD=90°,LBAC=60°.则AB·CD等于( )
A.-2 B.2 C.-2/3 D.2/3
3.已知lal=4, lbl=8,a与b的夹角是120°,
当a+2b与ka-b的夹角为钝角时,k的取值范围为
3.利用空间向量数量积求向量夹角
4.(2021天津西青期末)如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,P是C1D1的中点,则B1C·A1P=
,B1C与A1P所成角的大小为
4.利用空间向量数量积判断或证明垂直问题
例3 如图1.1-13,m,n是平面a内的两条相交直线.如果l垂直m,l垂直n,
求证:l垂直a.
THANKS
