第24章 圆 单元检测试题（含答案）

中小学教育资源及组卷应用平台
第二十四章《圆》单元检测题
题号 一 二 三 总分
19 20 21 22 23 24
分数
一、选择题(每题3分，共30分)
1．下列语句中，正确的是（　　）
A．长度相等的弧是等弧
B．在同一平面上的三点确定一个圆
C．三角形的内心是三角形三边垂直平分线的交点
D．三角形的外心到三角形三个顶点的距离相等
2．圆有（　　）条对称轴．
A．0 B．1 C．2 D．无数
3．如图，点A、O、D以及点B、O、C分别在一条直线上，则圆中弦的条数是（　　）
A．2条 B．3条 C．4条 D．5条
4．如图，⊙O的直径为10，弦AB的长为6，P为弦AB上的动点，则线段OP长的取值范围是（　　）
A．3≤OP≤5 B．4＜OP＜5 C．4≤OP≤5 D．3＜OP＜5
5．如图，圆心为C、直径为MN的半圆上有不同的两点A、B，在CN上有一点P，∠CBP＝∠CAP＝10°，若的度数是40°，则的度数是（　　）
A．10° B．15° C．20° D．25°
6．如图，在圆内接四边形ABCD中，∠B＝50°，则∠D＝（　　）
A．40° B．130° C．120° D．150°
7．在⊙O中，弦AB=8cm，直径为16cm，则弦AB所对的圆周角为（　　）
A．60° B．120° C．60°或120° D．30°或150°
8．将弧长为2πcm、圆心角为120°的扇形围成一个圆锥的侧面，则这个圆锥的高是（　　）
A． cm B．2 cm C．2 cm D． cm
9．在正六边形ABCDEF的中，若BE=10，则这个正六边形外接圆半径是（　　）
A． B．5 C． D．5
10．如图，在Rt△ABC中，∠ABC=90°，AC=4，AB=2，以点B为圆心，AB为半径画弧，交AC于点D，交BC于点E，连接BD，则图中阴影部分面积为（　　）
A． B． C． D．
二、填空题(每题3分，共24分)
11．如图是央行发布的建国70周年纪念银币的背面图案，这枚纪念币的周长是21.98厘米，它的直径是　 　厘米，面积是　 　平方厘米（π取3.14）．
12．到点P的距离等于2cm的点的集合是　 　．
13．下列说法正确的是（　 　）填序号．
①半径不等的圆叫做同心圆； ②优弧一定大于劣弧；
③不同的圆中不可能有相等的弦； ④直径是同一个圆中最长的弦．
14．线段AD过圆心O，交⊙O于点C、D．∠A＝24°，AE交⊙O于点B，且CD＝2AB，则∠EOD＝　 　．
15．如图，在半径为的⊙O中，AB，CD是互相垂直的两条弦，垂足为P，且AB＝CD＝4，则OP的长为　 　．
16．已知在半径为3的⊙O中，弦AB的长为4，那么圆心O到AB的距离为　 　．
17．如图，在⊙O中，，∠AOB＝50°，则∠COD＝　 　．
18．如图，点A、B、C在⊙O上，且∠AOB＝50°，则∠ACB＝　 　°．
三.解答题(共46分,19题6分，20 ---24题8分)
19．如图， ， 分别与⊙O相切于 ， 两点，点 在⊙O上，已知 ，求 的度数．
20．如图，AB是⊙O的直径，AE平分∠BAF交⊙O于E，过E点作直线与AF垂直交AF延长线于D点，且交AB于C点．
求证：CD与⊙O相切于点E．
21．如图，△ABC是⊙O的内接三角形，AB为⊙O的直径，AB＝6，AD平分∠BAC，交BC于点E，交⊙O于点D，连接BD.
(1)求证：∠BAD＝∠CBD；
(2)若∠AEB＝125°，求的长(结果保留π)．
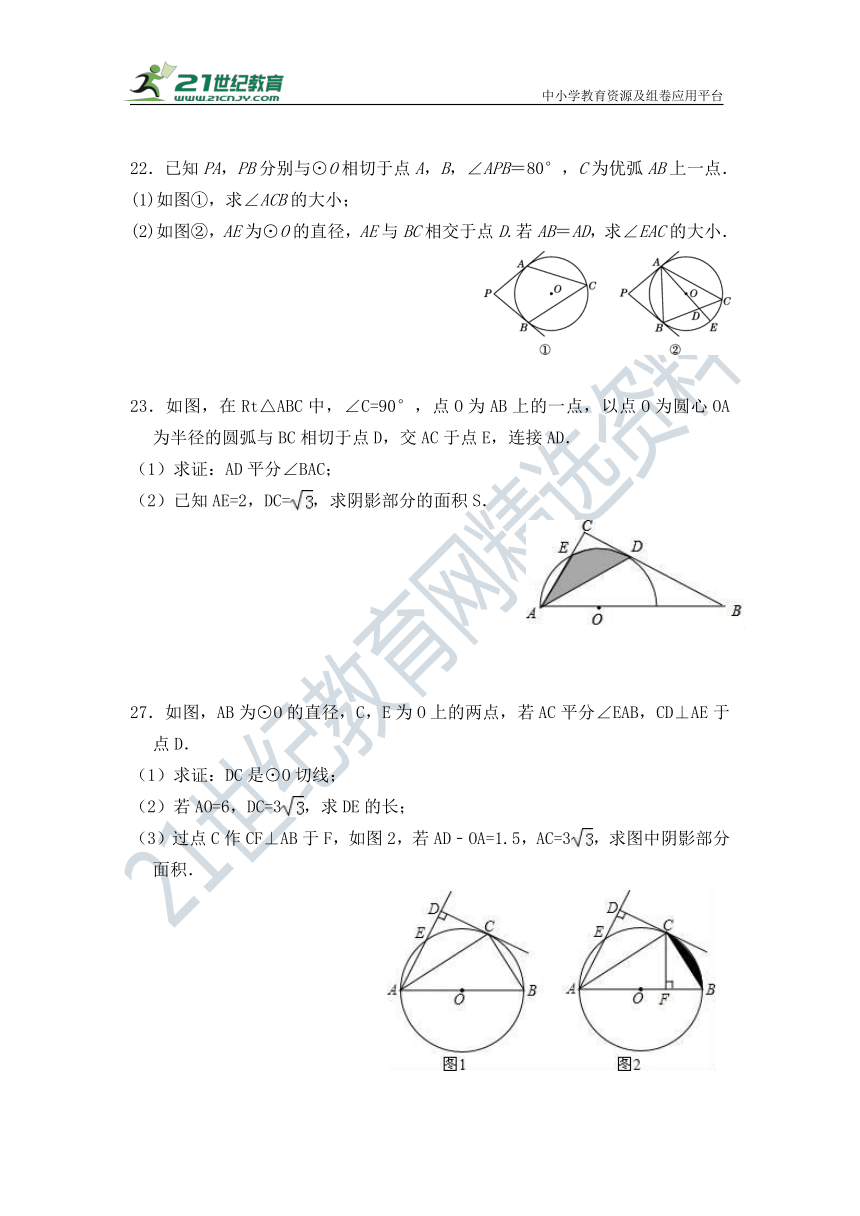
22．已知PA，PB分别与⊙O相切于点A，B，∠APB＝80°，C为优弧AB上一点．
(1)如图①，求∠ACB的大小；
(2)如图②，AE为⊙O的直径，AE与BC相交于点D.若AB＝AD，求∠EAC的大小．
23．如图，在Rt△ABC中，∠C=90°，点O为AB上的一点，以点O为圆心OA为半径的圆弧与BC相切于点D，交AC于点E，连接AD．
（1）求证：AD平分∠BAC；
（2）已知AE=2，DC=，求阴影部分的面积S．
27．如图，AB为⊙O的直径，C，E为O上的两点，若AC平分∠EAB，CD⊥AE于点D．
（1）求证：DC是⊙O切线；
（2）若AO=6，DC=3，求DE的长；
（3）过点C作CF⊥AB于F，如图2，若AD﹣OA=1.5，AC=3，求图中阴影部分面积．
　
参考答案
一、选择题(每题3分，共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 D D B C D A D B B B
二、填空题(每题3分，共24分)
11．解：由题意得，直径＝21.98÷3.14＝7，面积＝π×＝π；
故答案为：7，π．
12．解：到点P的距离等于2cm的点的集合是以P为圆心，以2cm为半径的圆．
故答案为：以P为圆心，以2cm为半径的圆．
13．解：①半径不等的圆叫做同心圆，错误；
②优弧一定大于劣弧，错误；
③不同的圆中不可能有相等的弦，错误；
④直径是同一个圆中最长的弦，正确．
故答案为：④．
14．解：连接OB，∵AB＝OC＝OB，
∴∠BOC＝∠A＝24°，
∠EBO＝2∠A＝48°，
∵OE＝OB
∴∠E＝∠EBO＝48°，
∴∠EOD＝∠A+∠E＝24°+48°＝72°．
故答案是：72°．
15．解：作OE⊥AB于E，OF⊥CD于F，连接OD、OB，
则AE＝BE＝AB＝2，DF＝CF＝CD＝2，
在Rt△OBE中，OB＝，BE＝2，
∴OE＝＝1，
同理可得OF＝1，
∵AB⊥CD，OE⊥AB，OF⊥CD，
∴四边形OEPF为矩形，
∵OE＝OF＝1，
∴四边形OEPF为正方形，
∴OP＝OE＝，
故答案为：．
16．解：作OC⊥AB于C，连接OA，如图，
∵OC⊥AB，
∴AC＝BC＝AB＝×4＝2，
在Rt△AOC中，OA＝5，
∴OC＝＝＝，
即圆心O到AB的距离为．
故答案为：．
17．解：∵＝，
∴∠COD＝∠AOB，
∵∠AOB＝50°，
∴∠COD＝50°，
故答案是：50°．
18．解：∵∠AOB＝50°，
∴∠ACB＝∠AOB＝25°，
故答案为：25．
三.解答题(共46分,19题6分，20 ---24题8分)
19．解：连接OA、OB，
∵PA、PB是⊙O切线，
∴PA⊥OA，PB⊥OB，
∴∠PAO=∠PBO=90°，
∵∠P+∠PAO+∠AOB+∠PBO=360°，
∴∠P=180°-∠AOB，
∵∠C=65°，
∴∠AOB=2∠C=130°，
∴∠P=180°-130°=50°
20、证明：连结OE
∵AE平分∠BAF
∴∠BAE＝∠FAE
∵OE＝OA
∴∠BAE＝∠OEA
∴∠FAE＝∠OEA
∴OE∥AD
∵AD⊥CD
∴OE⊥CD
∴CD与⊙O相切于E
21．(1)证明：∵AD平分∠BAC，
∴∠BAD＝∠CAD.
又∵∠CBD＝∠CAD，
∴∠BAD＝∠CBD.
(2)解：连接OD.
∵∠AEB＝125°，∴∠AEC＝55°.
∵AB为⊙O的直径，
∴∠ACE＝90°.
∴∠CAE＝35°.
∴∠DAB＝35°.
则所对圆心角∠DOB＝70°.
∴的长为＝π.
22．解：(1)连接OA，OB.
∵PA，PB是⊙O的切线，
∴∠OAP＝∠OBP＝90°.
∴∠AOB＝360°－90°－90°－80°＝100°.
∴∠ACB＝∠AOB＝50°.
(2)连接CE.
∵AE为⊙O的直径，∴∠ACE＝90°.
∵∠ACB＝50°，
∴∠BCE＝90°－50°＝40°.
∴∠BAE＝∠BCE＝40°.
∵AB＝AD，∴∠ABD＝∠ADB＝70°.
∴∠EAC＝∠ADB－∠ACB＝20°.
23．【解答】
（1）证明：连接OD．
∵BC是⊙O的切线，
∴OD⊥BC，
∴∠ODB=∠C=90°，
∴OD∥AC，
∴∠ODA=∠CAD，
∵OA=OD，
∴∠ODA=∠OAD，
∴∠CAD=∠OAD，
∴AD平分∠CAB．
（2）作OH⊥AC于H，连接OE．
∵OH⊥AC，
∴AH=EH=AE=1，
∵OD∥AC，OH∥CD，
∴四边形OHCD是平行四边形，
∵∠C=90°，
∴四边形OHCD是矩形，
∴OH=CD=，
在Rt△AOH中，OA===2，
∵cos∠HAO==，
∴∠HAO=60°，
∵OA=OE，
∴△AOE是等边三角形，
∴∠AOE=60°，
∵∠EAD=∠HAO=30°，
∴∠DOE=2∠EAD=60°，
连接DE，
∵OE=OD，
∴△DOE是等边三角形，
∴∠DEO=60°，
∴∠DEO=∠AOE=60°，
∴DE∥AB，
∴S△AED=S△ODE，
∴S阴=S扇形EOD==．
24．【解答】（1）证明：连接OC，如图1，
∵AC平分∠EAB，
∴∠1=∠2，
∵OA=OC，
∴∠2=∠3，
∴∠1=∠3，
∴OC∥AD，
∵AD⊥CD，
∴OC⊥CD，
∴DC是⊙O切线；
（2）解：连接BE交OC于H，如图1，
∵AB为⊙O的直径，
∴∠AEB=90°，
∵OC∥AD，
∴∠OHB=90°，
∴EH=BH，四边形CDEH为矩形，
∴CD=EH=3，CH=ED，
∴BH=3，
在Rt△OBH中，OH==3，
∴CH=6﹣3=3，
∴DE=3；
（3）解：连接OC，如图2，设⊙O的半径为r，
∵AC平分∠BAD，CD⊥AD，CF⊥AB，
∴CD=CF，
∴AD=AF=AO+OF，
∵AD﹣OA=1.5，
∴AO+OF﹣OA=1.5，即OF=1.5，
∵AB为⊙O的直径，
∴∠ACB=90°，
∵∠CAF=∠BAC，
∴△ACF∽△ABC，
∴=，即=，解得r=﹣（舍去）或r=3，
在Rt△OCF中，cos∠COF==，
∴∠COF=60°，
∴CF=OF=，
∴图中阴影部分面积=S扇形BOC﹣S△OCB=﹣×3×=π﹣．