12.2 一次函数图像与性质(2)课件
文档属性
| 名称 | 12.2 一次函数图像与性质(2)课件 |  | |
| 格式 | zip | ||
| 文件大小 | 319.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-09-22 08:20:56 | ||
图片预览






文档简介
课件23张PPT。
沪科版八年级数学上
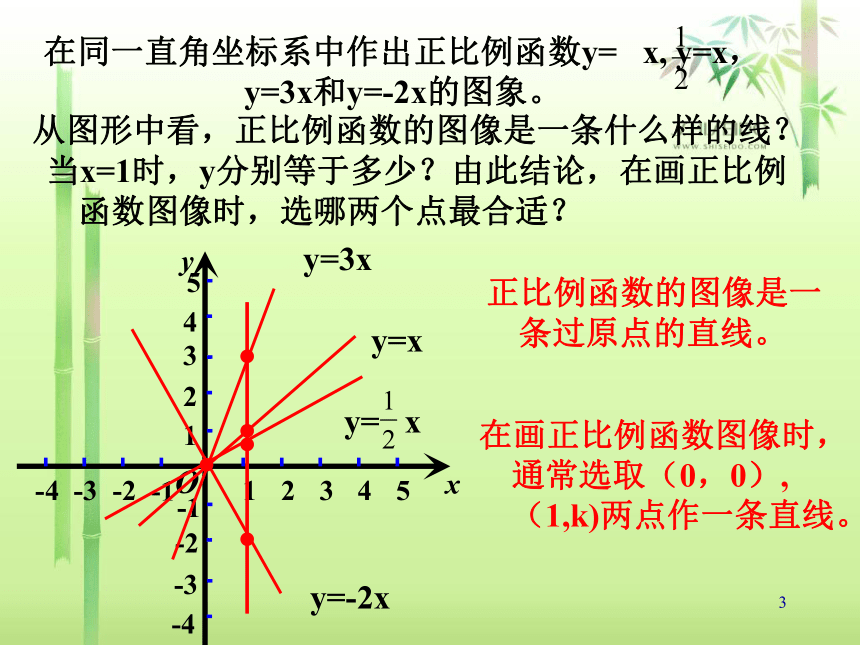
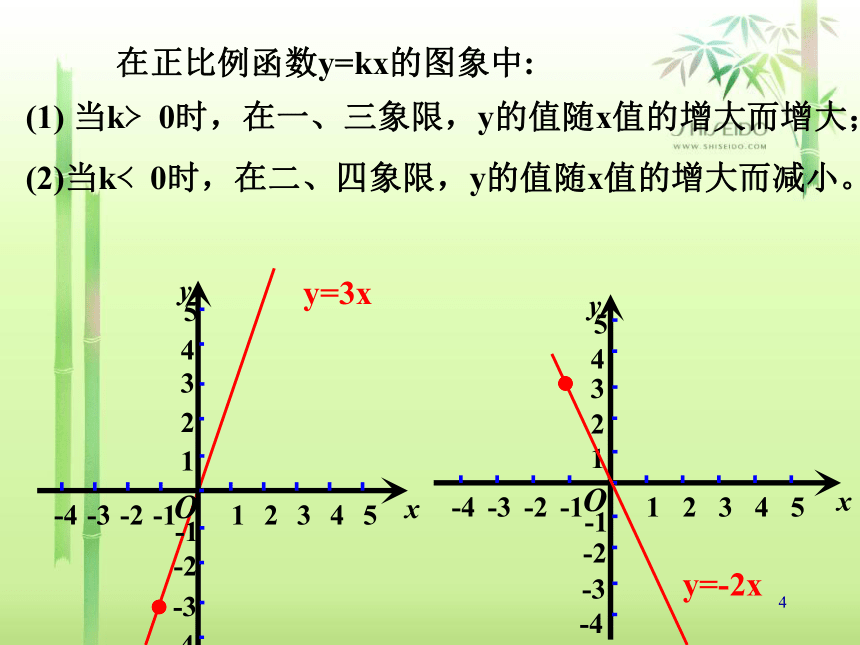
12.2 一次函数图像与性质(2)2(1)列表(2)描点(3)连线2、画函数图象的一般步骤:1.什么是一次函数?什么是正比例函数?如果y=kx+b(k,b是常数,k≠0),那么y叫做x的函数。特别的,当b=0时,y=kx+b就成为y=kx,这时,y叫做x的正比例函数。你还记得吗?3在同一直角坐标系中作出正比例函数y= x, y=x,y=3x和y=-2x的图象。y= xy=xy=3xy=-2x从图形中看,正比例函数的图像是一条什么样的线?正比例函数的图像是一条过原点的直线。当x=1时,y分别等于多少?由此结论,在画正比例函数图像时,选哪两个点最合适?在画正比例函数图像时,通常选取(0,0),(1,k)两点作一条直线。4 在正比例函数y=kx的图象中:(1) 当k?0时,在一、三象限,y的值随x值的增大而增大;(2)当k?0时,在二、四象限,y的值随x值的增大而减小。y=3xy=-2x5正比例函数的性质1.正比例函数y=kx的图象是经过(0,0),(1,k)的一条直线。2.当k?0时,图象在一、三象限,y随x的增大而增大;
当k?0时,图象在二、四象限,y随x的增大而减小。61.函数y=4x的图象经过点(0,__)与点(1,__),图象经过第____象限,y随x的增大而____.
2.函数y=-2x的图象经过点(0,__)与点(1,__),图象经过第____象限,y随x的增大而____.练一练,你会了吗?04一.三增大0-2二.四减小7一次函数又如何取两点作图?通常是x取0,算出y值;再取y为0,算出x值。
如作y=-3x+2函数的图象
应怎样立表?8作函数y=2x+3、
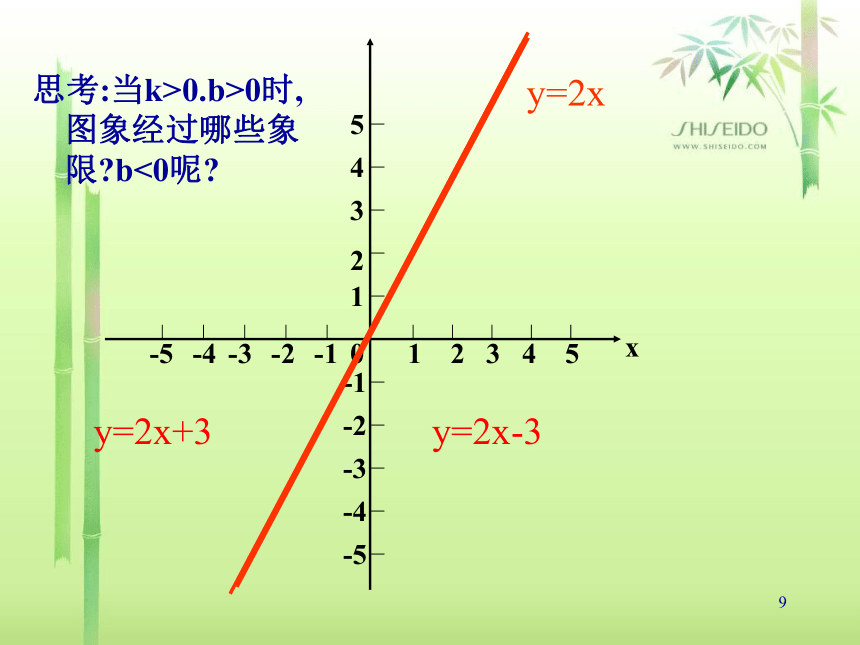
y=2x、y=2x-3图象。9y=2xy=2x+3y=2x-3思考:当k>0.b>0时,图象经过哪些象限?b<0呢?10作函数y=-2x、 y=-2x+3、 y=-2x-3图象。
11y=-2xy=-2x+3y=-2x-3思考:当k<0.b>0时,图象经过哪些象限?b<0呢?12y=2x+3y=2x-3从图中可以看出:k>0时,y随x的增大而增大.13y=-2x+3y=-2x-3从图中可以看出:k<0时,y随x的增大而减小.14结论15根据图象确定k,b的取值K 0
b 0K 0
b 0K 0
b 0K 0
b 0K 0
b 0K 0
b 0K
b>
=<
=<
><
<>
<>
>16
1 一次函数y=x-2的图象不经过的象限为( )
(A) 一 (B) 二 (C) 三 (D) 四
2 不经过第二象限的直线是 ( )
(A) y=-2x+4 (B) y=2x-1 (C) y=2x+1 (D) y=-2x+1
3 若直线 y=kx+b经过一二四象限,那么直线 y=-bx+k经过 象限
4 直线 y=kx-k的图象的大致位置是 ( )
ABCDBB二三四C171.求出下列函数的解析式
(1)将直线y=5x向下平移6个单位;
(2)将直线 向上平移3个单位.
2.已知一次函数y=(1-2k)x+(2k+1)
(1)当k取何值时,y随x的增大而增大?
(2)当k取何值时,函数图象经过坐标系原点?
(3)当k取何值时,函数图象不经过第四象限?快马加鞭18 已知一次函数y=kx+b的图象经过点(-1, 5),且与正比例函数y=- x/2的图象相交于点(2,a),求:
(1)a的值
(2)k,b的值
(3)这两个函数图象与x轴所围成的三角形面积. (1)∵正比例函数y=- x/2的图象经过点(2,a),解:∴a=- 2/2=-1(2)∵一次函数y=kx+b的图象经过点(-1,5)、(2,-1)∴∴19 已知一次函数y=kx+b的图象经过点(-1, 5),且与正比例函数y=- x/2的图象相交于点(2,a),求:
(1)a的值
(2)k,b的值
(3)这两个函数图象与x轴所围成的三角形面积. 解:(3)如图,设 y=-2x+3与 x轴交于点A,两直线交于PAOP当y=0时,-2x+3=0,∴x=1.5∴点A(1.5,0)∴SΔOAP=1.5X1x1/2=3/4∵直线y=-2x+3与y=-x/2交于点P
∴点P的坐标为(2,-1)20通过本节课的学习,你有哪些收获?
提示:可以从学习知识.学习方法等方面来总结.感悟与收获21
(1)已知直线y=kx+b平行于直线y=-2x+1,且过点(-2,4),分别求出k和b。
(2)一次函数y=4x-3和y=-4x-3的图象分别经过________象限和_______象限,它们的交点坐标是______.
(3)已知一次函数y=(2-m)x+m+2,那么
(a)当m为何值时,它的图象经过原点;
(b)当m为何值时,它的图象经过点(-1,5);
(c)当m为何值时,它的图象不经过第二象限。作业22如图,在直角坐标系中,直线y=kx+4与x 轴正半轴交于一点A,与y轴交于点B,已知△OAB的面积为10,求这条直线的解析式。 课外思考23结论
沪科版八年级数学上
12.2 一次函数图像与性质(2)2(1)列表(2)描点(3)连线2、画函数图象的一般步骤:1.什么是一次函数?什么是正比例函数?如果y=kx+b(k,b是常数,k≠0),那么y叫做x的函数。特别的,当b=0时,y=kx+b就成为y=kx,这时,y叫做x的正比例函数。你还记得吗?3在同一直角坐标系中作出正比例函数y= x, y=x,y=3x和y=-2x的图象。y= xy=xy=3xy=-2x从图形中看,正比例函数的图像是一条什么样的线?正比例函数的图像是一条过原点的直线。当x=1时,y分别等于多少?由此结论,在画正比例函数图像时,选哪两个点最合适?在画正比例函数图像时,通常选取(0,0),(1,k)两点作一条直线。4 在正比例函数y=kx的图象中:(1) 当k?0时,在一、三象限,y的值随x值的增大而增大;(2)当k?0时,在二、四象限,y的值随x值的增大而减小。y=3xy=-2x5正比例函数的性质1.正比例函数y=kx的图象是经过(0,0),(1,k)的一条直线。2.当k?0时,图象在一、三象限,y随x的增大而增大;
当k?0时,图象在二、四象限,y随x的增大而减小。61.函数y=4x的图象经过点(0,__)与点(1,__),图象经过第____象限,y随x的增大而____.
2.函数y=-2x的图象经过点(0,__)与点(1,__),图象经过第____象限,y随x的增大而____.练一练,你会了吗?04一.三增大0-2二.四减小7一次函数又如何取两点作图?通常是x取0,算出y值;再取y为0,算出x值。
如作y=-3x+2函数的图象
应怎样立表?8作函数y=2x+3、
y=2x、y=2x-3图象。9y=2xy=2x+3y=2x-3思考:当k>0.b>0时,图象经过哪些象限?b<0呢?10作函数y=-2x、 y=-2x+3、 y=-2x-3图象。
11y=-2xy=-2x+3y=-2x-3思考:当k<0.b>0时,图象经过哪些象限?b<0呢?12y=2x+3y=2x-3从图中可以看出:k>0时,y随x的增大而增大.13y=-2x+3y=-2x-3从图中可以看出:k<0时,y随x的增大而减小.14结论15根据图象确定k,b的取值K 0
b 0K 0
b 0K 0
b 0K 0
b 0K 0
b 0K 0
b 0K
b>
=<
=<
><
<>
<>
>16
1 一次函数y=x-2的图象不经过的象限为( )
(A) 一 (B) 二 (C) 三 (D) 四
2 不经过第二象限的直线是 ( )
(A) y=-2x+4 (B) y=2x-1 (C) y=2x+1 (D) y=-2x+1
3 若直线 y=kx+b经过一二四象限,那么直线 y=-bx+k经过 象限
4 直线 y=kx-k的图象的大致位置是 ( )
ABCDBB二三四C171.求出下列函数的解析式
(1)将直线y=5x向下平移6个单位;
(2)将直线 向上平移3个单位.
2.已知一次函数y=(1-2k)x+(2k+1)
(1)当k取何值时,y随x的增大而增大?
(2)当k取何值时,函数图象经过坐标系原点?
(3)当k取何值时,函数图象不经过第四象限?快马加鞭18 已知一次函数y=kx+b的图象经过点(-1, 5),且与正比例函数y=- x/2的图象相交于点(2,a),求:
(1)a的值
(2)k,b的值
(3)这两个函数图象与x轴所围成的三角形面积. (1)∵正比例函数y=- x/2的图象经过点(2,a),解:∴a=- 2/2=-1(2)∵一次函数y=kx+b的图象经过点(-1,5)、(2,-1)∴∴19 已知一次函数y=kx+b的图象经过点(-1, 5),且与正比例函数y=- x/2的图象相交于点(2,a),求:
(1)a的值
(2)k,b的值
(3)这两个函数图象与x轴所围成的三角形面积. 解:(3)如图,设 y=-2x+3与 x轴交于点A,两直线交于PAOP当y=0时,-2x+3=0,∴x=1.5∴点A(1.5,0)∴SΔOAP=1.5X1x1/2=3/4∵直线y=-2x+3与y=-x/2交于点P
∴点P的坐标为(2,-1)20通过本节课的学习,你有哪些收获?
提示:可以从学习知识.学习方法等方面来总结.感悟与收获21
(1)已知直线y=kx+b平行于直线y=-2x+1,且过点(-2,4),分别求出k和b。
(2)一次函数y=4x-3和y=-4x-3的图象分别经过________象限和_______象限,它们的交点坐标是______.
(3)已知一次函数y=(2-m)x+m+2,那么
(a)当m为何值时,它的图象经过原点;
(b)当m为何值时,它的图象经过点(-1,5);
(c)当m为何值时,它的图象不经过第二象限。作业22如图,在直角坐标系中,直线y=kx+4与x 轴正半轴交于一点A,与y轴交于点B,已知△OAB的面积为10,求这条直线的解析式。 课外思考23结论
