3.1.2 等式的性质 教案
图片预览



文档简介
第三章 一元一次方程
3.1 从算式到方程
3.1.2 等式的性质
一、教学目标
【知识与技能】
1.能用文字和数学式子表达等式的两个性质.
2.能用等式的性质解简单的一元一次方程.
【过程与方法】
经历利用天平的经验分析得出等式的性质的过程.
【情感态度与价值观】
培养学生合作交流的探索精神.
二、课型
新授课
三、课时
1课时。
四、教学重难点
【教学重点】
理解等式的性质,并能利用其解一元一次方程.
【教学难点】
能熟练运用等式的性质对方程进行变形.
五、课前准备
教师:课件、直尺、天平、砝码等。
学生:三角尺、练习本、钢笔或圆珠笔、铅笔。
六、教学过程
(一)导入新课
同学们,观察图中天平状态
思考:如果在平衡的天平的两边都加(或减)同样的量,天平还保持平衡吗?(出示课件2)
(二)探索新知
1.师生互动,探究等式的性质1
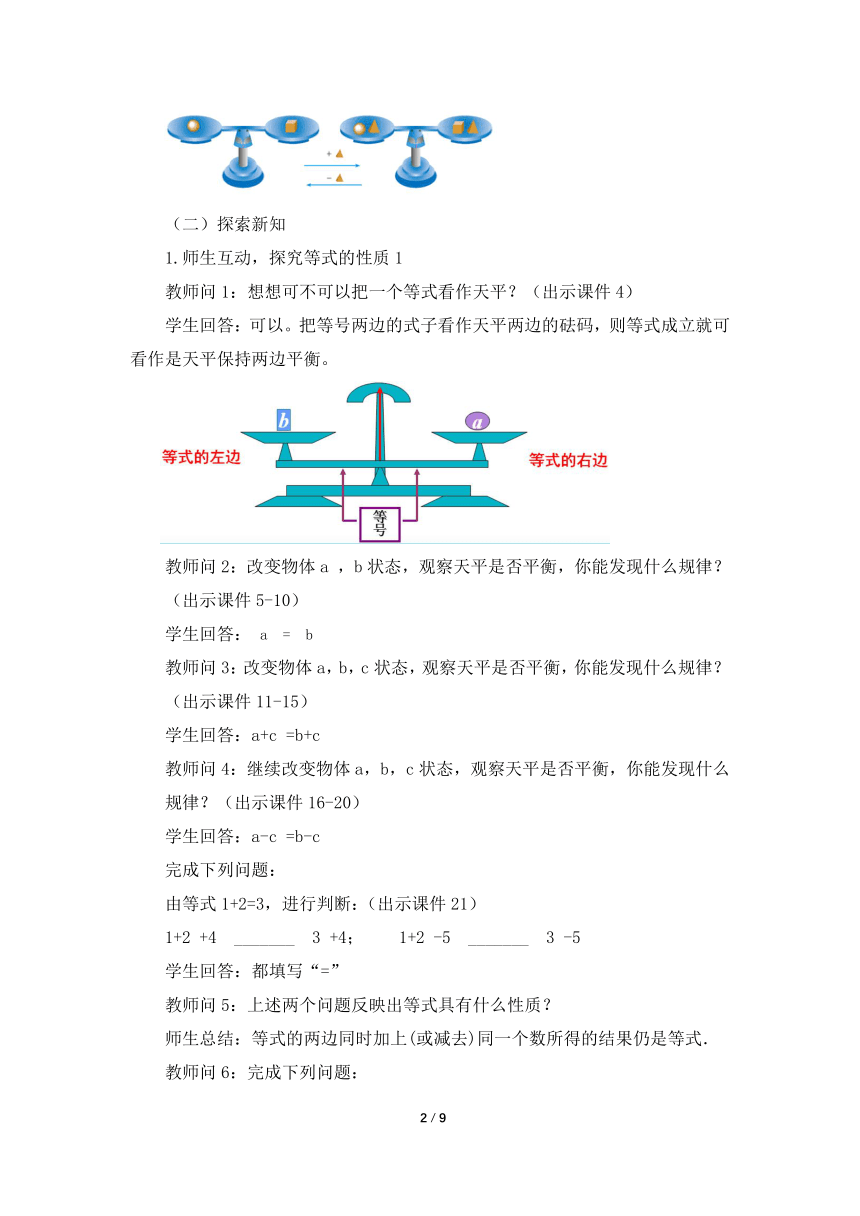
教师问1:想想可不可以把一个等式看作天平?(出示课件4)
学生回答:可以。把等号两边的式子看作天平两边的砝码,则等式成立就可看作是天平保持两边平衡。
教师问2:改变物体a ,b状态,观察天平是否平衡,你能发现什么规律?(出示课件5-10)
学生回答: a = b
教师问3:改变物体a,b,c状态,观察天平是否平衡,你能发现什么规律?
(出示课件11-15)
学生回答:a+c =b+c
教师问4:继续改变物体a,b,c状态,观察天平是否平衡,你能发现什么规律?(出示课件16-20)
学生回答:a-c =b-c
完成下列问题:
由等式1+2=3,进行判断:(出示课件21)
1+2 +4 _______ 3 +4; 1+2 -5 _______ 3 -5
学生回答:都填写“=”
教师问5:上述两个问题反映出等式具有什么性质?
师生总结:等式的两边同时加上(或减去)同一个数所得的结果仍是等式.
教师问6:完成下列问题:
由等式2x+3x=5x,进行判断:(出示课件22)
2x+3x +4x _______ 5x +4x; 2x+3x -x _______ 5x -x
学生回答:填写“=”
教师问7:上述两个问题反映出等式具有什么性质?
师生总结:等式的两边同时加上(或减去)同一个式子,所得的结果仍是等式.
总结点拨:(出示课件23)
等式的性质1:
等式的两边同时加上(或减去)同一个数或同一个式子,所得的结果仍是等式.
教师问8:等式的性质1用式子的形式怎样表示?
学生回答:如果a=b,那么a±c=b±c.
总结点拨:(出示课件24)
换言之,
等式的性质1
等式两边同时加 (或减) 同一个数 (或式子),结果仍相等.
如果a=b,那么a±c=b±c.
2.探究等式的性质2
教师问9:改变物体a,b状态,观察天平的变化,你能发现什么规律?(出示课件26-29)
学生回答:a = b;2a = 2b;3a = 3b;ac = bc
教师问10:同样地,若将物体a,b同时缩小相同的倍数,你能发现什么规律?
学生回答:;;(c≠0)
教师问11:除数c能为0吗?
学生回答:不能为0.
教师问12:由等式3m+5m=8m,进行判断:(出示课件31)
2×( 3m+5m ) _______2×8m; ( 3m+5m ) ÷2 _______ 8m÷2.
学生回答:都填写“=”.
教师问13:上述两个问题反映出等式具有什么性质?
学生回答:等式两边同时乘同一个数,或除以同一个不为0的数,结果仍相等. (出示课件32)
教师问14:用代数式子的形式怎样表示?
学生回答:如果a=b,那么ac=bc;(出示课件33)
如果a=b(c≠0),那么 .
总结点拨:(出示课件34)
等式的性质
性质1:等式两边同时加(或减)同一个数(或式子),结果仍相等.
性质2:等式两边同时乘同一个数,或除以同一个不为0的数,结果仍相等.
注意:
1.等式两边都要参加运算,且是同一种运算.
2.等式两边加或减,乘或除以的数一定是同一个数或同一个式子.
3.等式两边不能都除以0,即0不能作除数或分母.
例: (1) 怎样从等式 x-5= y-5 得到等式 x = y (出示课件35)
(2) 怎样从等式 3+x=1 得到等式 x =-2
(3) 怎样从等式 4x=12 得到等式 x =3
(4) 怎样从等式 得到等式 a = b
师生共同解答如下:
(1)依据等式的性质1两边同时加5.
(2)依据等式的性质1两边同时减3.
(3)依据等式的性质2两边同时除以4或同乘 .
(4)依据等式的性质2两边同时除以 或同乘100.
例:已知mx=my,下列结论错误的是 ( )(出示课件37)
A. x=y B. a+mx=a+my
C. mx-y=my-y D. amx=amy
师生共同解答如下:
解析:根据等式的性质1,可知B、C正确;根据等式的性质2,可知D正确;根据等式的性质2,A选项只有m≠0时才成立,故A错误.
答案:A
总结点拨:此类判断等式变形是否正确的题型中,尤其注意利用等式的性质2等式两边同除以某个字母,只有这个字母确定不为0时,等式才成立.
例:利用等式的性质解下列方程:(出示课件39)
(1) x + 7 = 26;
师生共同解答如下:
解: 方程两边同时减去7,得:x + 7 -7 = 26-7
x=19
总结点拨:解一元一次方程要“化归”为“ x=a ”的形式.
(2) -5x = 20;(出示课件40)
师生共同解答如下:
思考:为使 (2) 中未知项的系数化为1,将要用到等式的什么性质 ?
解: 方程两边同时除以-5,得:-5x÷(-5)= 20 ÷(-5).
化简得:x=-4.
(3)-x-5=4 . (出示课件41)
师生共同解答如下:
思考:对比(1),(3)有什么新特点 ?
解:方程两边同时加上5,得:
-x-5+5=4+5,
化简得:-x=9
方程两边同时乘-3,得:x=-27.
思考:x=-27是原方程的解吗
一般地,从方程解出未知数的值以后,可以代入原方程检验,看这个值能否使方程的两边相等.
例如,将 x = -27 代入方程-x-5=4 的左边,
-×(-27)-5=9-5=4
方程的左右两边相等,所以 x = -27 是原方程的解.
总结点拨:(出示课件44)
经过对原方程的一系列变形(两边同加减、乘除),最终把方程化为最简的等式: x = a(常数)
即方程左边只一个未知数项、且未知数项的系数是 1,右边只一个常数项.
(三)课堂练习(出示课件45-52)
1.如图所示,两个天平都平衡,则三个球体的重量等于( )个正方体的重量.
A.2 B.3 C.4 D.5
2. 下列说法正确的是( )
A. 等式都是方程
B. 方程都是等式
C. 不是方程的就不是等式
D. 未知数的值就是方程的解
3. 下列各式变形正确的是 ( )
A. 由3x-1= 2x+1得3x-2x =1+1
B. 由5+1= 6得5= 6+1
C. 由2(x+1) = 2y+1得x +1= y +1
D. 由2a + 3b = c-6 得2a = c-18b
4. 下列变形,正确的是 ( )
A. 若ac = bc,则a = b
B. 若 ,则a = b
C. 若a2 = b2,则a = b
D. 若 ,则x = -2
5. 填空.
(1) 将等式x-3=5 的两边都_____得到x =8 ,这是根据等式的性质__;
(2) 将等式 的两边都乘以___或除以 ___得到 x = -2,这是根据等式性质 ___;
(3) 将等式x + y =0的两边都_____得到x = -y,这是根据等式的性质___;
(4) 将等式 xy =1的两边都______得到 y=,这是根 据等式的性质___.
6.利用等式的性质解下列方程并检验:
(1)x-5=6;(2)x=45÷0.3; (3)5x=-4;(4)-x=1
7. 已知关于x的方程 mx+=6 和方程3x -10 =5的解相同,求m的值.
参考答案:
1.D 解析:设一个球体重x,圆柱重y,正方体重z,根据等量关系列方程2x=5y,2z=3y,消去y可得:x=z,则3x=5z,即三个球体的重量等于五个正方体的重量.
2.B
3.A
4.B
5.(1)加3,1;(2)2,,2;(3)减y,1;(4)除以x,2.
6. 解:(1)x-5=6;
x=6+5
x=11
检验:把x=11代入方程的左边,得6,等于右边,所以x=11是方程的解.
(2)x=45÷0.3;
x=150
检验:把x=150代入方程的左边,得45,等于右边,所以x=150是方程的解.
(3)5x=-4;
x=-0.8
检验:把x=-0.8代入方程的左边,得-4,等于右边,所以 x=-0.8是方程的解.
(4)-x=1
x=-4
检验:把x=-4代入方程的左边,得1,等于右边,所以x=-4是方程的解.
7. 解:方程3x-10 =5的解为x =5,将其代入方程 mx+=6,得到m+=6,解得m =2.
(四)课堂小结
今天我们学了哪些内容:
1.等式的性质1:等式的两边同时加(或减)同一个代数式,所得结果仍是等式.
即如果a=b,那么a±c=b±c.
2.等式的性质2 :等式两边乘同一个数,或除以同一个不为0的数,结果仍是等式.
即如果a=b,那么ac=bc;如果a=b(c≠0),那么.
3. 利用等式的基本性质解一元一次方程
(五)课前预习
预习下节课(3.2)86页到87页的相关内容。
了解解一元一次方程的步骤.
七、课后作业
1、教材83页练习
2、用等式的性质解下列方程:
(1)4x+7=3;
(2) =4.
八、板书设计:
九、教学反思:
本节课采用从生活中的跷跷板入手,激发学生学习兴趣,采用类比等式性质创设问题情景的方法,引导学生的自主探究活动,教给学生类比、猜想、验证等研究问题的方法,培养学生善于动手、善于观察、善于思考的学习习惯。利用学生的好奇心设疑、解疑,组织活泼互动、有效的教学活动,学生积极参与,大胆猜想,使学生在自主探索和合作交流中理解和掌握本节课的内容。力求在整个探究学习的过程充满师生之间、生生之间的交流和互动,体现教师是教学活动的组织者、引导者、合作者,学生才是学习的主体。
2 / 10
3.1 从算式到方程
3.1.2 等式的性质
一、教学目标
【知识与技能】
1.能用文字和数学式子表达等式的两个性质.
2.能用等式的性质解简单的一元一次方程.
【过程与方法】
经历利用天平的经验分析得出等式的性质的过程.
【情感态度与价值观】
培养学生合作交流的探索精神.
二、课型
新授课
三、课时
1课时。
四、教学重难点
【教学重点】
理解等式的性质,并能利用其解一元一次方程.
【教学难点】
能熟练运用等式的性质对方程进行变形.
五、课前准备
教师:课件、直尺、天平、砝码等。
学生:三角尺、练习本、钢笔或圆珠笔、铅笔。
六、教学过程
(一)导入新课
同学们,观察图中天平状态
思考:如果在平衡的天平的两边都加(或减)同样的量,天平还保持平衡吗?(出示课件2)
(二)探索新知
1.师生互动,探究等式的性质1
教师问1:想想可不可以把一个等式看作天平?(出示课件4)
学生回答:可以。把等号两边的式子看作天平两边的砝码,则等式成立就可看作是天平保持两边平衡。
教师问2:改变物体a ,b状态,观察天平是否平衡,你能发现什么规律?(出示课件5-10)
学生回答: a = b
教师问3:改变物体a,b,c状态,观察天平是否平衡,你能发现什么规律?
(出示课件11-15)
学生回答:a+c =b+c
教师问4:继续改变物体a,b,c状态,观察天平是否平衡,你能发现什么规律?(出示课件16-20)
学生回答:a-c =b-c
完成下列问题:
由等式1+2=3,进行判断:(出示课件21)
1+2 +4 _______ 3 +4; 1+2 -5 _______ 3 -5
学生回答:都填写“=”
教师问5:上述两个问题反映出等式具有什么性质?
师生总结:等式的两边同时加上(或减去)同一个数所得的结果仍是等式.
教师问6:完成下列问题:
由等式2x+3x=5x,进行判断:(出示课件22)
2x+3x +4x _______ 5x +4x; 2x+3x -x _______ 5x -x
学生回答:填写“=”
教师问7:上述两个问题反映出等式具有什么性质?
师生总结:等式的两边同时加上(或减去)同一个式子,所得的结果仍是等式.
总结点拨:(出示课件23)
等式的性质1:
等式的两边同时加上(或减去)同一个数或同一个式子,所得的结果仍是等式.
教师问8:等式的性质1用式子的形式怎样表示?
学生回答:如果a=b,那么a±c=b±c.
总结点拨:(出示课件24)
换言之,
等式的性质1
等式两边同时加 (或减) 同一个数 (或式子),结果仍相等.
如果a=b,那么a±c=b±c.
2.探究等式的性质2
教师问9:改变物体a,b状态,观察天平的变化,你能发现什么规律?(出示课件26-29)
学生回答:a = b;2a = 2b;3a = 3b;ac = bc
教师问10:同样地,若将物体a,b同时缩小相同的倍数,你能发现什么规律?
学生回答:;;(c≠0)
教师问11:除数c能为0吗?
学生回答:不能为0.
教师问12:由等式3m+5m=8m,进行判断:(出示课件31)
2×( 3m+5m ) _______2×8m; ( 3m+5m ) ÷2 _______ 8m÷2.
学生回答:都填写“=”.
教师问13:上述两个问题反映出等式具有什么性质?
学生回答:等式两边同时乘同一个数,或除以同一个不为0的数,结果仍相等. (出示课件32)
教师问14:用代数式子的形式怎样表示?
学生回答:如果a=b,那么ac=bc;(出示课件33)
如果a=b(c≠0),那么 .
总结点拨:(出示课件34)
等式的性质
性质1:等式两边同时加(或减)同一个数(或式子),结果仍相等.
性质2:等式两边同时乘同一个数,或除以同一个不为0的数,结果仍相等.
注意:
1.等式两边都要参加运算,且是同一种运算.
2.等式两边加或减,乘或除以的数一定是同一个数或同一个式子.
3.等式两边不能都除以0,即0不能作除数或分母.
例: (1) 怎样从等式 x-5= y-5 得到等式 x = y (出示课件35)
(2) 怎样从等式 3+x=1 得到等式 x =-2
(3) 怎样从等式 4x=12 得到等式 x =3
(4) 怎样从等式 得到等式 a = b
师生共同解答如下:
(1)依据等式的性质1两边同时加5.
(2)依据等式的性质1两边同时减3.
(3)依据等式的性质2两边同时除以4或同乘 .
(4)依据等式的性质2两边同时除以 或同乘100.
例:已知mx=my,下列结论错误的是 ( )(出示课件37)
A. x=y B. a+mx=a+my
C. mx-y=my-y D. amx=amy
师生共同解答如下:
解析:根据等式的性质1,可知B、C正确;根据等式的性质2,可知D正确;根据等式的性质2,A选项只有m≠0时才成立,故A错误.
答案:A
总结点拨:此类判断等式变形是否正确的题型中,尤其注意利用等式的性质2等式两边同除以某个字母,只有这个字母确定不为0时,等式才成立.
例:利用等式的性质解下列方程:(出示课件39)
(1) x + 7 = 26;
师生共同解答如下:
解: 方程两边同时减去7,得:x + 7 -7 = 26-7
x=19
总结点拨:解一元一次方程要“化归”为“ x=a ”的形式.
(2) -5x = 20;(出示课件40)
师生共同解答如下:
思考:为使 (2) 中未知项的系数化为1,将要用到等式的什么性质 ?
解: 方程两边同时除以-5,得:-5x÷(-5)= 20 ÷(-5).
化简得:x=-4.
(3)-x-5=4 . (出示课件41)
师生共同解答如下:
思考:对比(1),(3)有什么新特点 ?
解:方程两边同时加上5,得:
-x-5+5=4+5,
化简得:-x=9
方程两边同时乘-3,得:x=-27.
思考:x=-27是原方程的解吗
一般地,从方程解出未知数的值以后,可以代入原方程检验,看这个值能否使方程的两边相等.
例如,将 x = -27 代入方程-x-5=4 的左边,
-×(-27)-5=9-5=4
方程的左右两边相等,所以 x = -27 是原方程的解.
总结点拨:(出示课件44)
经过对原方程的一系列变形(两边同加减、乘除),最终把方程化为最简的等式: x = a(常数)
即方程左边只一个未知数项、且未知数项的系数是 1,右边只一个常数项.
(三)课堂练习(出示课件45-52)
1.如图所示,两个天平都平衡,则三个球体的重量等于( )个正方体的重量.
A.2 B.3 C.4 D.5
2. 下列说法正确的是( )
A. 等式都是方程
B. 方程都是等式
C. 不是方程的就不是等式
D. 未知数的值就是方程的解
3. 下列各式变形正确的是 ( )
A. 由3x-1= 2x+1得3x-2x =1+1
B. 由5+1= 6得5= 6+1
C. 由2(x+1) = 2y+1得x +1= y +1
D. 由2a + 3b = c-6 得2a = c-18b
4. 下列变形,正确的是 ( )
A. 若ac = bc,则a = b
B. 若 ,则a = b
C. 若a2 = b2,则a = b
D. 若 ,则x = -2
5. 填空.
(1) 将等式x-3=5 的两边都_____得到x =8 ,这是根据等式的性质__;
(2) 将等式 的两边都乘以___或除以 ___得到 x = -2,这是根据等式性质 ___;
(3) 将等式x + y =0的两边都_____得到x = -y,这是根据等式的性质___;
(4) 将等式 xy =1的两边都______得到 y=,这是根 据等式的性质___.
6.利用等式的性质解下列方程并检验:
(1)x-5=6;(2)x=45÷0.3; (3)5x=-4;(4)-x=1
7. 已知关于x的方程 mx+=6 和方程3x -10 =5的解相同,求m的值.
参考答案:
1.D 解析:设一个球体重x,圆柱重y,正方体重z,根据等量关系列方程2x=5y,2z=3y,消去y可得:x=z,则3x=5z,即三个球体的重量等于五个正方体的重量.
2.B
3.A
4.B
5.(1)加3,1;(2)2,,2;(3)减y,1;(4)除以x,2.
6. 解:(1)x-5=6;
x=6+5
x=11
检验:把x=11代入方程的左边,得6,等于右边,所以x=11是方程的解.
(2)x=45÷0.3;
x=150
检验:把x=150代入方程的左边,得45,等于右边,所以x=150是方程的解.
(3)5x=-4;
x=-0.8
检验:把x=-0.8代入方程的左边,得-4,等于右边,所以 x=-0.8是方程的解.
(4)-x=1
x=-4
检验:把x=-4代入方程的左边,得1,等于右边,所以x=-4是方程的解.
7. 解:方程3x-10 =5的解为x =5,将其代入方程 mx+=6,得到m+=6,解得m =2.
(四)课堂小结
今天我们学了哪些内容:
1.等式的性质1:等式的两边同时加(或减)同一个代数式,所得结果仍是等式.
即如果a=b,那么a±c=b±c.
2.等式的性质2 :等式两边乘同一个数,或除以同一个不为0的数,结果仍是等式.
即如果a=b,那么ac=bc;如果a=b(c≠0),那么.
3. 利用等式的基本性质解一元一次方程
(五)课前预习
预习下节课(3.2)86页到87页的相关内容。
了解解一元一次方程的步骤.
七、课后作业
1、教材83页练习
2、用等式的性质解下列方程:
(1)4x+7=3;
(2) =4.
八、板书设计:
九、教学反思:
本节课采用从生活中的跷跷板入手,激发学生学习兴趣,采用类比等式性质创设问题情景的方法,引导学生的自主探究活动,教给学生类比、猜想、验证等研究问题的方法,培养学生善于动手、善于观察、善于思考的学习习惯。利用学生的好奇心设疑、解疑,组织活泼互动、有效的教学活动,学生积极参与,大胆猜想,使学生在自主探索和合作交流中理解和掌握本节课的内容。力求在整个探究学习的过程充满师生之间、生生之间的交流和互动,体现教师是教学活动的组织者、引导者、合作者,学生才是学习的主体。
2 / 10
