4.3.3 余角和补角 教案
图片预览



文档简介
第四章 几何图形初步
4.3 角
4.3.3 余角和补角
一、教学目标
【知识与技能】
1.知道互为余角、互为补角的意义,会求一个角余角和补角的度数.
2.知道等角的补角或余角相等,培养初步的推理能力.
3.在具体情境中了解余角与补角.懂得等角的余角相等,等角的补角相等.并能运用这些性质解决一些简单的实际问题.
【过程与方法】
经历观察、操作、推理、交流等活动,发展学生的空间观念,培养学生的推理能力和有条理的表达能力;
【情感态度与价值观】
体验数学知识的发生、发展过程,敢于面对数学活动中的困难,建立学好数学的自信心.
二、课型
新授课
三、课时
1课时
四、教学重难点
【教学重点】
余角与补角的概念,等角的补角或余角相等.
【教学难点】
证明等角的补角或余角相等.
五、课前准备
教师:课件、三角尺、量角器、圆规、角的纸片数张等。
学生:三角尺、量角器、圆规、角的纸片数张、铅笔、钢笔或圆珠笔。
六、教学过程
(一)导入新课
让学生观察大坝图片.
如图坝底是由石块堆积而成,要测出∠1的度数,你有什么简单的方法吗?(出示课件2)
教师:要解决这问题,我们先来学习余角和补角.
(二)探索新知
1.师生互动,探究余角、补角的概念
如图:有两个角分别是∠1与∠2(出示课件4)
教师问1:如果把∠1与∠2这两个角拼在一起,也就是∠1+∠2.请问:∠1+∠2等于多少度?
学生回答:90°.
教师讲解:如果两个角的和等于90°( 直角 ),就说这两个角互为余角 ( 简称为两个角互余 ).
如上图,可以说∠1 是∠2 的余角,或∠2 是∠1的余角,或∠1和∠2互余.
教师问2:图中有两个角,∠3与∠4,把这两个角拼在一起,也就是∠3+∠4.∠3+∠4等于多少度?(出示课件6)
学生回答:180°.
总结点拨:如果两个角的和等于180°(平角),就说这两个角互为补角 ( 简称为两个角互补 ).
如图,可以说∠3 是∠4 的补角,或∠4是∠3 的补角,或∠3 和∠4 互补.
考点1:利用余角、补角的概念求角的度数(出示课件8)
例:若一个角的补角等于它的余角的 4 倍,求这个角的度数.
师生共同解答如下:
解:设这个角为 x°,则它的补角是 ( 180 –x )°,
余角是 ( 90 –x )° .
根据题意,得180 –x = 4 ( 90 –x ) .
解得 x = 60.
答:这个角的度数是 60 °.
考点2:余角、补角、角平分线相结合的题目(出示课件10)
例:如图,已知O为AD上一点,∠AOC与∠AOB互补,OM,ON分别为∠AOC,∠AOB的平分线,若∠MON=40°,试求∠AOC与∠AOB的度数.
师生共同解答如下:(出示课件11)
解:设∠AOB=x,
因为∠AOC与∠AOB互补,
则∠AOC=180°–x.
因为OM,ON分别为∠AOC,∠AOB的平分线,
所以∠AOM=(180°-x) , ∠AON= x .
所以(180°-x) -x=40°.
解得x=50°,则180°–x =130°.
即∠AOB=50°,∠AOC=130°.
2.师生互动,探究余角、补角的性质
思考:如图,∠1 与∠2,∠1 与∠3都互为补角,∠2 与∠3 的大小有什么关系? (出示课件15)
教师问3:∠1与∠2互补是什么意思?
学生回答:∠1+∠2=180°.
教师问4:∠1与∠3互补呢?
学生回答:∠1+∠3=180°.
教师问5:通过列出的关系式,思考怎么单独表示出∠2与∠3呢?
学生讨论后回答:∠2=180°–∠1;∠3=180°–∠1
教师问6:现在我们能知道∠2与∠3的关系了吗?
学生讨论后回答:∠2=∠3.
教师问7:我们能得到补角的一个什么性质呢?
教师讲解:同角(等角)的补角相等.
教师问8:类似的,你能得出同角的余角有什么性质吗?试着自己证明。
教师讲解:
教师问9:∠1 与∠2,∠3都互为余角,∠2 与∠3 的大小有什么关系?
学生回答:∠2=90°–∠1=∠3=90°–∠1
教师问10:由此你能得到什么?
学生回答:同角的余角相等.
总结点拨:
同角 (等角) 的补角相等.
同角 (等角) 的余角相等.
考点:余角和补角的识别
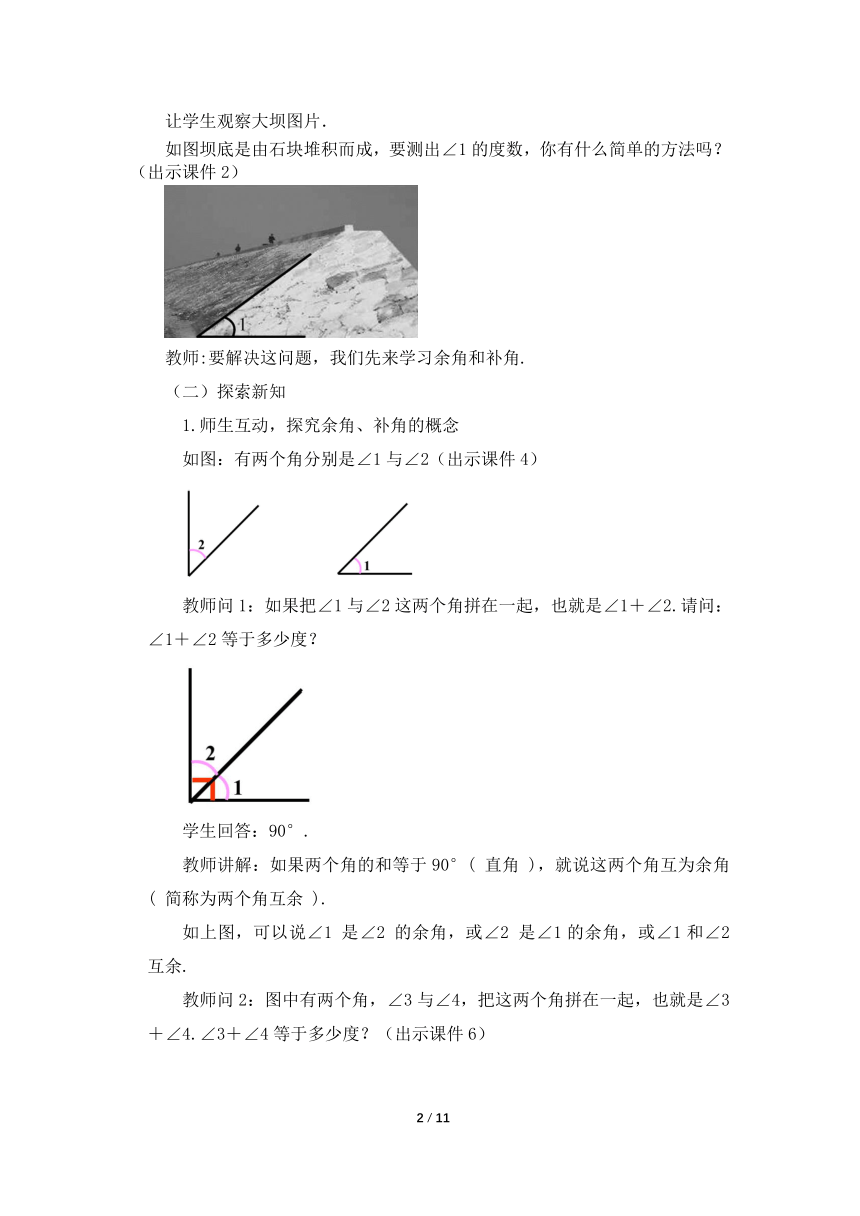
例:如图,点A,O,B在同一直线上,射线 OD 和射线 OE 分别平分∠AOC 和∠BOC,图中哪些角互为余角? (出示课件16)
师生共同解答如下:
解:因为点A,O,B在同一直线上,所以∠AOC和∠BOC 互为补角.
又因为射线 OD 和射线 OE 分别平分∠AOC 和∠BOC,
所以∠COD+∠COE = ∠AOC+∠BOC= (∠AOC+∠BOC ) = 90°.
所以∠COD和∠COE互为余角,
同理∠AOD和∠BOE,∠AOD和∠COE,∠COD和∠BOE也互为余角.
3.师生互动,探究方位角
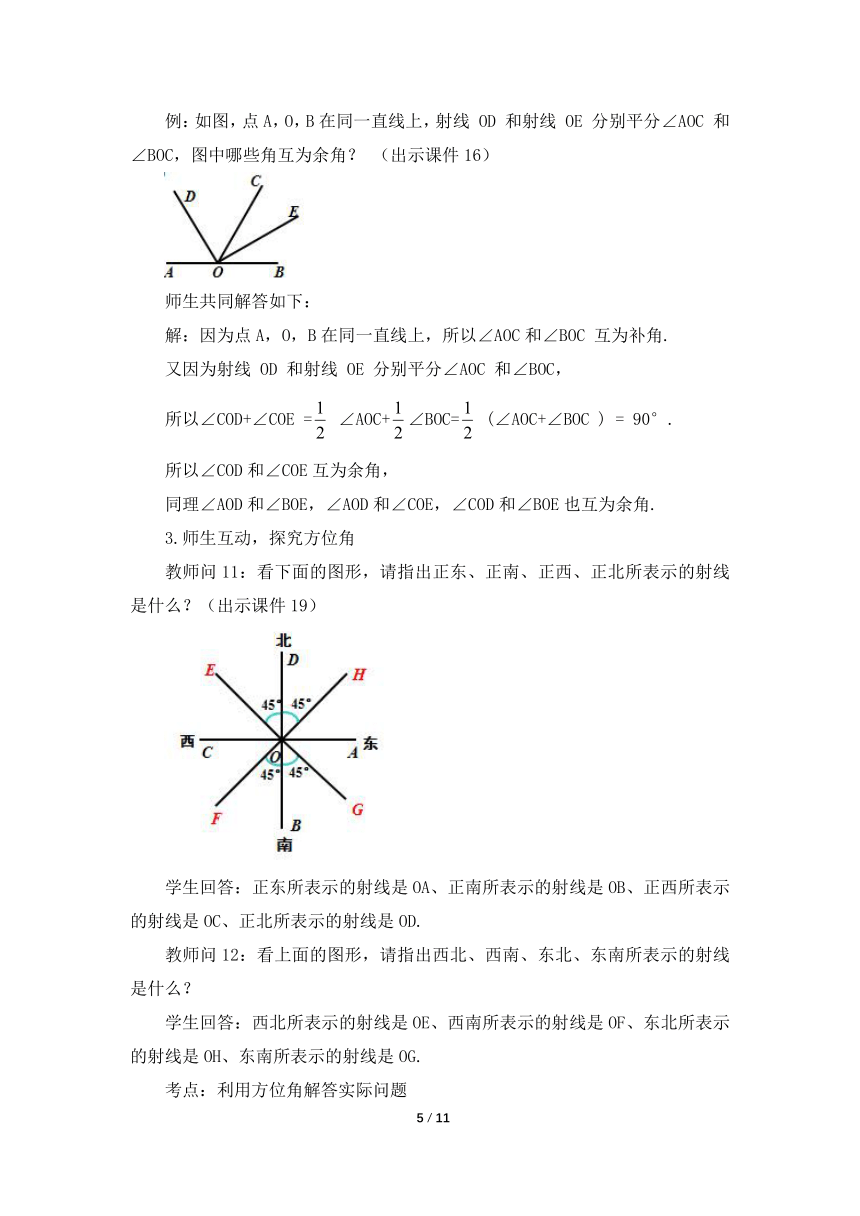
教师问11:看下面的图形,请指出正东、正南、正西、正北所表示的射线是什么?(出示课件19)
学生回答:正东所表示的射线是OA、正南所表示的射线是OB、正西所表示的射线是OC、正北所表示的射线是OD.
教师问12:看上面的图形,请指出西北、西南、东北、东南所表示的射线是什么?
学生回答:西北所表示的射线是OE、西南所表示的射线是OF、东北所表示的射线是OH、东南所表示的射线是OG.
考点:利用方位角解答实际问题
例:如图,货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上.同时,在它北偏东40°,南偏西10°,西北(即北偏西45°)方向上又分别发现了客轮B,货轮C和海岛D.仿照表示灯塔方位的方法画出表示客轮B,货轮C和海岛D方向的射线.(出示课件21)
师生共同解答如下:
(三)课堂练习(出示课件24-30)
1.若一个角为65°,则它的补角的度数为( )
A.25° B.35° C.115° D.125°
2.如图,快艇从P处向正北航行到A处时,向左转50°航行到B处,再向右转80°继续航行,此时的航行方向为( )
A.北偏东30° B.北偏东80° C.北偏西30° D.北偏西50°
3. 一个角的余角是它的2倍,这个角的度数是( )
A.30° B.45° C.60° D.75°
4. 下列说法正确的是( )
A.一个角的补角一定大于它本身
B.一个角的余角一定小于它本身
C.一个钝角减去一个锐角的差一定是一个锐角
D.一个角的余角一定小于其补角
5. 如图,将一副三角尺按不同的位置摆放,下列方式中∠α与∠β互余的是 ( )
A.图① B.图② C.图③ D.图④
6. ∠α=35°,则∠α的补角为______度.
7. 如图,已知∠ACB=∠CDB=90°.
(1) 图中有哪几对互余的角?
(2) 图中哪几对角是相等的角(直角除外)?为什么?
8. 一个角的补角是它的3倍,这个角是多少度
9. 垃圾打捞船 A 和 B 都停驻在湖边观测湖面,从 A 船发现它的北偏东60°方向有白色漂浮物, 同时,从 B 船也发现该白色漂浮物在它的北偏西30°方向.
(1) 试在图中确定白色漂浮物C的位置;
(2) 点 C 在点 A 的北偏东60°的方向上,那么点 A在点 C 的______方向上.
A. 南偏东30°
B. 南偏西30°
C. 南偏东60°
D. 南偏西60°
参考答案:
1.C
2.A 解析:如图,因为∠2=∠1=50°.∠3=∠4 –∠2=80°–50°=30°,此时的航行方向为北偏东30°.
3.A
4.D
5.A
6.145
7.(1)∠A+∠B=90°, ∠A+∠2=90°,∠1+∠B=90°, ∠1+∠2=90°.
(2)∠B=∠2, ( 同角的余角相等 )
∠A=∠1. ( 同角的余角相等 )
8.解: 设这个角为x°,则它的补角为(180°– x°),
得: 180 – x=3x
解得:x = 45
答: 这个角是45°.
9.解:(1)
(2)D 解析:如下图所示:
(四)课堂小结
今天我们学了哪些内容:
1.互余、互补
(1)和为90°的两个角互余;
(2)和为180°的两个角互补.
2.方位角
(五)课前预习
预习下节课(4.4)的相关内容。
知道制作长方体的材料
七、课后作业
1、教材138-139页练习1,2,3,4
2、如图所示,甲、乙、丙三艘轮船从港口O出发,当分别行驶到A、B、C处时,经测量得甲船位于港口的北偏东44°方向,乙船位于港口的北偏东76°方向,丙船位于港口的北偏西45°方向.
(1)求∠BOC的度数;
(2)求∠AOB的度数.
八、板书设计:
九、教学反思:
通过实物图建筑激发学生的学习兴趣,再运用现代化的教学手段,把图形的“静”变成“动”,在动态课件演示中引出概念,增强了趣味性,并且可以充分调动学生的学习兴趣,一下子把学生吸引到课堂上来.这样也把书本上原本呆板的概念激活了,使数学知识充满新鲜感,实现了书本知识和学生发现的一种沟通,增强学生对几何图形的敏感性.
1 / 13
4.3 角
4.3.3 余角和补角
一、教学目标
【知识与技能】
1.知道互为余角、互为补角的意义,会求一个角余角和补角的度数.
2.知道等角的补角或余角相等,培养初步的推理能力.
3.在具体情境中了解余角与补角.懂得等角的余角相等,等角的补角相等.并能运用这些性质解决一些简单的实际问题.
【过程与方法】
经历观察、操作、推理、交流等活动,发展学生的空间观念,培养学生的推理能力和有条理的表达能力;
【情感态度与价值观】
体验数学知识的发生、发展过程,敢于面对数学活动中的困难,建立学好数学的自信心.
二、课型
新授课
三、课时
1课时
四、教学重难点
【教学重点】
余角与补角的概念,等角的补角或余角相等.
【教学难点】
证明等角的补角或余角相等.
五、课前准备
教师:课件、三角尺、量角器、圆规、角的纸片数张等。
学生:三角尺、量角器、圆规、角的纸片数张、铅笔、钢笔或圆珠笔。
六、教学过程
(一)导入新课
让学生观察大坝图片.
如图坝底是由石块堆积而成,要测出∠1的度数,你有什么简单的方法吗?(出示课件2)
教师:要解决这问题,我们先来学习余角和补角.
(二)探索新知
1.师生互动,探究余角、补角的概念
如图:有两个角分别是∠1与∠2(出示课件4)
教师问1:如果把∠1与∠2这两个角拼在一起,也就是∠1+∠2.请问:∠1+∠2等于多少度?
学生回答:90°.
教师讲解:如果两个角的和等于90°( 直角 ),就说这两个角互为余角 ( 简称为两个角互余 ).
如上图,可以说∠1 是∠2 的余角,或∠2 是∠1的余角,或∠1和∠2互余.
教师问2:图中有两个角,∠3与∠4,把这两个角拼在一起,也就是∠3+∠4.∠3+∠4等于多少度?(出示课件6)
学生回答:180°.
总结点拨:如果两个角的和等于180°(平角),就说这两个角互为补角 ( 简称为两个角互补 ).
如图,可以说∠3 是∠4 的补角,或∠4是∠3 的补角,或∠3 和∠4 互补.
考点1:利用余角、补角的概念求角的度数(出示课件8)
例:若一个角的补角等于它的余角的 4 倍,求这个角的度数.
师生共同解答如下:
解:设这个角为 x°,则它的补角是 ( 180 –x )°,
余角是 ( 90 –x )° .
根据题意,得180 –x = 4 ( 90 –x ) .
解得 x = 60.
答:这个角的度数是 60 °.
考点2:余角、补角、角平分线相结合的题目(出示课件10)
例:如图,已知O为AD上一点,∠AOC与∠AOB互补,OM,ON分别为∠AOC,∠AOB的平分线,若∠MON=40°,试求∠AOC与∠AOB的度数.
师生共同解答如下:(出示课件11)
解:设∠AOB=x,
因为∠AOC与∠AOB互补,
则∠AOC=180°–x.
因为OM,ON分别为∠AOC,∠AOB的平分线,
所以∠AOM=(180°-x) , ∠AON= x .
所以(180°-x) -x=40°.
解得x=50°,则180°–x =130°.
即∠AOB=50°,∠AOC=130°.
2.师生互动,探究余角、补角的性质
思考:如图,∠1 与∠2,∠1 与∠3都互为补角,∠2 与∠3 的大小有什么关系? (出示课件15)
教师问3:∠1与∠2互补是什么意思?
学生回答:∠1+∠2=180°.
教师问4:∠1与∠3互补呢?
学生回答:∠1+∠3=180°.
教师问5:通过列出的关系式,思考怎么单独表示出∠2与∠3呢?
学生讨论后回答:∠2=180°–∠1;∠3=180°–∠1
教师问6:现在我们能知道∠2与∠3的关系了吗?
学生讨论后回答:∠2=∠3.
教师问7:我们能得到补角的一个什么性质呢?
教师讲解:同角(等角)的补角相等.
教师问8:类似的,你能得出同角的余角有什么性质吗?试着自己证明。
教师讲解:
教师问9:∠1 与∠2,∠3都互为余角,∠2 与∠3 的大小有什么关系?
学生回答:∠2=90°–∠1=∠3=90°–∠1
教师问10:由此你能得到什么?
学生回答:同角的余角相等.
总结点拨:
同角 (等角) 的补角相等.
同角 (等角) 的余角相等.
考点:余角和补角的识别
例:如图,点A,O,B在同一直线上,射线 OD 和射线 OE 分别平分∠AOC 和∠BOC,图中哪些角互为余角? (出示课件16)
师生共同解答如下:
解:因为点A,O,B在同一直线上,所以∠AOC和∠BOC 互为补角.
又因为射线 OD 和射线 OE 分别平分∠AOC 和∠BOC,
所以∠COD+∠COE = ∠AOC+∠BOC= (∠AOC+∠BOC ) = 90°.
所以∠COD和∠COE互为余角,
同理∠AOD和∠BOE,∠AOD和∠COE,∠COD和∠BOE也互为余角.
3.师生互动,探究方位角
教师问11:看下面的图形,请指出正东、正南、正西、正北所表示的射线是什么?(出示课件19)
学生回答:正东所表示的射线是OA、正南所表示的射线是OB、正西所表示的射线是OC、正北所表示的射线是OD.
教师问12:看上面的图形,请指出西北、西南、东北、东南所表示的射线是什么?
学生回答:西北所表示的射线是OE、西南所表示的射线是OF、东北所表示的射线是OH、东南所表示的射线是OG.
考点:利用方位角解答实际问题
例:如图,货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上.同时,在它北偏东40°,南偏西10°,西北(即北偏西45°)方向上又分别发现了客轮B,货轮C和海岛D.仿照表示灯塔方位的方法画出表示客轮B,货轮C和海岛D方向的射线.(出示课件21)
师生共同解答如下:
(三)课堂练习(出示课件24-30)
1.若一个角为65°,则它的补角的度数为( )
A.25° B.35° C.115° D.125°
2.如图,快艇从P处向正北航行到A处时,向左转50°航行到B处,再向右转80°继续航行,此时的航行方向为( )
A.北偏东30° B.北偏东80° C.北偏西30° D.北偏西50°
3. 一个角的余角是它的2倍,这个角的度数是( )
A.30° B.45° C.60° D.75°
4. 下列说法正确的是( )
A.一个角的补角一定大于它本身
B.一个角的余角一定小于它本身
C.一个钝角减去一个锐角的差一定是一个锐角
D.一个角的余角一定小于其补角
5. 如图,将一副三角尺按不同的位置摆放,下列方式中∠α与∠β互余的是 ( )
A.图① B.图② C.图③ D.图④
6. ∠α=35°,则∠α的补角为______度.
7. 如图,已知∠ACB=∠CDB=90°.
(1) 图中有哪几对互余的角?
(2) 图中哪几对角是相等的角(直角除外)?为什么?
8. 一个角的补角是它的3倍,这个角是多少度
9. 垃圾打捞船 A 和 B 都停驻在湖边观测湖面,从 A 船发现它的北偏东60°方向有白色漂浮物, 同时,从 B 船也发现该白色漂浮物在它的北偏西30°方向.
(1) 试在图中确定白色漂浮物C的位置;
(2) 点 C 在点 A 的北偏东60°的方向上,那么点 A在点 C 的______方向上.
A. 南偏东30°
B. 南偏西30°
C. 南偏东60°
D. 南偏西60°
参考答案:
1.C
2.A 解析:如图,因为∠2=∠1=50°.∠3=∠4 –∠2=80°–50°=30°,此时的航行方向为北偏东30°.
3.A
4.D
5.A
6.145
7.(1)∠A+∠B=90°, ∠A+∠2=90°,∠1+∠B=90°, ∠1+∠2=90°.
(2)∠B=∠2, ( 同角的余角相等 )
∠A=∠1. ( 同角的余角相等 )
8.解: 设这个角为x°,则它的补角为(180°– x°),
得: 180 – x=3x
解得:x = 45
答: 这个角是45°.
9.解:(1)
(2)D 解析:如下图所示:
(四)课堂小结
今天我们学了哪些内容:
1.互余、互补
(1)和为90°的两个角互余;
(2)和为180°的两个角互补.
2.方位角
(五)课前预习
预习下节课(4.4)的相关内容。
知道制作长方体的材料
七、课后作业
1、教材138-139页练习1,2,3,4
2、如图所示,甲、乙、丙三艘轮船从港口O出发,当分别行驶到A、B、C处时,经测量得甲船位于港口的北偏东44°方向,乙船位于港口的北偏东76°方向,丙船位于港口的北偏西45°方向.
(1)求∠BOC的度数;
(2)求∠AOB的度数.
八、板书设计:
九、教学反思:
通过实物图建筑激发学生的学习兴趣,再运用现代化的教学手段,把图形的“静”变成“动”,在动态课件演示中引出概念,增强了趣味性,并且可以充分调动学生的学习兴趣,一下子把学生吸引到课堂上来.这样也把书本上原本呆板的概念激活了,使数学知识充满新鲜感,实现了书本知识和学生发现的一种沟通,增强学生对几何图形的敏感性.
1 / 13
