22.2.1配方法课件

课件10张PPT。 配方法开心练一练： (1) (2)2、下列方程能用直接开平方法来解吗?创设情境 温故探新1、用直接开平方法解下列方程:静心想一想：(1)(2)(3)能否把(3)转化成(x+b)2=a(a≥0)的
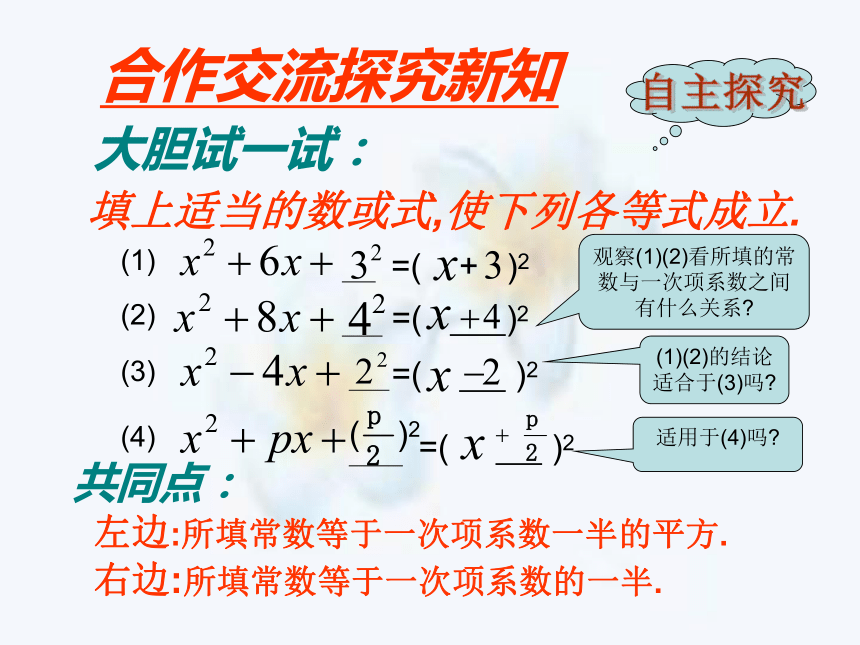
形式呢?(1)(2)(3)=( + )2=( )2=( )2左边:所填常数等于一次项系数一半的平方.右边:所填常数等于一次项系数的一半.填上适当的数或式,使下列各等式成立.大胆试一试：共同点： ( )2=( )2(4)合作交流探究新知自主探究观察(1)(2)看所填的常数与一次项系数之间有什么关系?(1)(2)的结论适合于(3)吗? 适用于(4)吗?现在你会解方程 吗?把常数项移到方程右边得：两边同加上 得： 即两边直接开平方得：合作交流探究新知
解:∴原方程的解为自主探究如何配方?例1: 用配方法解方程解:配方得：开平方得：范例研讨运用新知移项得：∴原方程的解为：一次项系数变为负又如何配方呢?例2: 你能用配方法解方程
吗？解:配方得：开平方得：范例研讨运用新知移项得：∴原方程的解为：化二次项系数为1得：二次项系数不为1
又怎么办?想一想用配方法
解一元二次方程
一般有哪些步骤?例2: 你能用配方法解方程
吗？反馈练习巩固新知= ( + )2= ( - )2(2)(1)( )1、填空:( )认真做一做： （3） ( ) = ( - )2 （4） ( ) = ( - )2你一定能行!反馈练习巩固新知2、用配方法解下列方程:3、用配方法将下列式子化成a(x+h)2+k的形式。 (1)x2+8x-15=0(2)x2-5x-6=0(3)2x2-5x-6=0(4) x2+px+q=0(p2-4q＞ 0) (3) -3x2-2x+1 (2) x2-x+1 (1) y2+y-2课堂小结布置作业小结：（2）移项（3）配方（4）开平方
（5）写出方程的解
思考题：1.已知x是实数,求y=x2-4x+5的最小值.2、用配方法解一元二次方程 ax2+bx+c=0(a≠0) 的步骤：1、配方法： 通过配方,将方程的左边化成一个含未知数的完全平方式,右边是一个非负常数,运用直接开平方求出方程的解的方法。
2.已知x2+y2-4x+8y+20=0,灵活应用配方法求x+y的值.3.借助配方法任写一个代数式使它的值恒大于0.(1)化二次项系数为1今天你有哪些收获?谢谢指导再见