数学人教A版(2019)必修第一册5.2.1三角函数的概念 说课课件(共26张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册5.2.1三角函数的概念 说课课件(共26张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 65.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-24 00:00:00 | ||
图片预览


文档简介
(共26张PPT)
5.2.1三角函数的概念
人教2019A版必修 第一册
说课流程
学情分析
教材分析
教法学法分析
教学过程分析
板书设计
教学评价分析
01
02
03
06
05
04
目录
CONTENTS
5.1
任意角和弧度制
三角函数的概念
5.2
4
指数函数
与对数函数
3
函数的概念与性质
3.3幂函数
诱导公式
5.3
三角函数的图像与性质
5.4
5.5
三角恒等变换
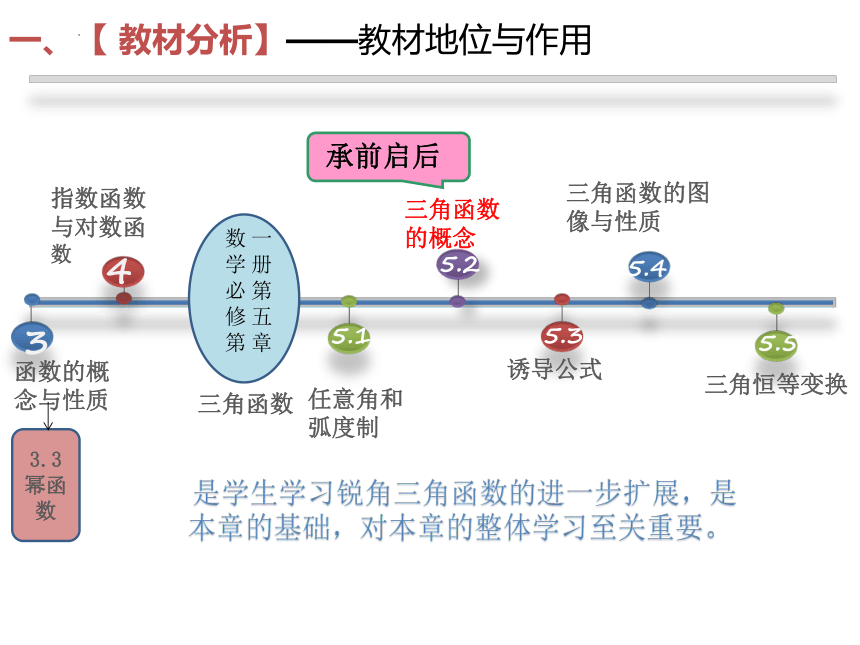
承前启后
是学生学习锐角三角函数的进一步扩展,是 本章的基础,对本章的整体学习至关重要。
一、【 教材分析】——教材地位与作用
三角函数
数学必修第一册第五章
一、【 教材分析】——教学目标
借助单位圆理解任意角三角函数的定义;
01
能初步运用定义分析和解决与三角函数值有关的一些简单问题;
02
体验三角函数概念的产生、发展过程,领悟直角坐标系的工具功能,丰富数形结合的经验。
03
数学建模
利用单位圆刻画点的变化情况
数学抽象
三角函数的定义
逻辑推理
三角函数概念的推导过程
数学运算
根据定义求三角函数值
直观想象
三角函数第二定义的推导
一、【 教材分析】——核心素养
重点:
借助单位圆理解任意角三角函数(正弦、余弦、正切)的定义
难点:
1.任意角的三角函数概念的建构过程;
2.角的终边与单位圆的交点坐标。
解决办法:通过复习引入新课,建立知识间的联系,提高学生的抽象概括能力。
一、【 教材分析】——教学重点与难点
1.在初中,学生已学了锐角三角函数。
2. 圆的有关知识。
3.在本章第一节“任意角与弧度制”的内容中学生会用坐标找出任意角与象限角,能够把以前学过的角度在弧度制下表示出来。
学生具备: 学生通过前面函数的学习,已初步具有逻辑思维能力,能在教师的引导下独立解决简单问题。
学生欠缺: 数形结合能力不强,望“函数”而“色变”,数学抽象的素养欠缺
二、【 学情分析】
知识基础
1
2
能力基础
心理特点
高一的学生精力旺盛,好奇心强,喜欢刺激惊险的活动。
3
合作探究
巩固练习
竞赛比拼
三、教法学法分析
基于以上的学情分析,为了突出重点,突破难点,
本节课的教法与学法如下:
三、【 教法学法分析】
问题引领
例题精析
变式练习
学法
学案导学
亲身实践
教法
引导学生主动思考
提高学生合作意识
培养学生规范答题
锻炼学生动手能力
培养自学能力
激发求知欲望
激发学生荣誉感,活动中学习
升华学习内容
四、教学过程分析
另外留1分钟机动
复习旧知,引入新课
(5分钟)
探究新知,形成概念
(15分钟)
例题学习,理解概念(8分钟)
归纳总结,提高认识
(2分钟)
当堂练习,巩固概念
(5分钟)
竞赛比拼,深化概念
(3分钟)
课后作业,巩固提高
(1分钟)
四、【 教学过程分析】
二、课堂教学
一、课前准备
教师准备
学生准备
1、编写学案 2、制作课件 3、多媒体
1、预习教材 2、完成学案相关内容
四、【 教学过程】——复习旧知,引入新课
设计意图:共同回顾,为后面探究任意角的三角函数作了铺垫。
温故知新,让学生体会知识的产生、发展过程。
由于学生的基础比较差,前面学过的知识容易遗忘,我采用复习旧知的方式,引入新课
四、【 教学过程】——探究新知,形成概念(定义1)
设计意图:通过问题1,引导学生建立坐标系,求点P的坐标,为探究1做准备。
为了完成函数的第一次抽象,我设计了问题1
四、【 教学过程】——探究新知,形成概念(定义1)
设计意图:通过分组探究、教师指导的形式,让学生能求角的终边与单位圆的交点坐标,进而明白其确定性。并突破本节课的难点2。通过问题2,即体现了由特殊到一般的特点,同时为三角函数的概念起着铺垫的作用。
问题2:一般地,任意给定一个角 ,它的终边OP与单位圆交点P的坐标能唯一确定吗?
为完成函数概念的第二次抽象,设计了探究1
学生活动:小组探究,派代表上黑板板书探究的结果。
四、【 教学过程】——探究新知,形成概念(定义1)
设计意图:在这里及时讨论函数的定义域,更直观,学生更容易理解,特别是正切函数的定义域一目了然。
通过探究1,得出三角函数的定义,学习了函数就要研究函数的定义域,下面通过小组讨论完成这一任务。
正弦函数、余弦函数、正切函数都是以角为自变量,以单位圆上点的坐标或坐标的比值为函数值的函数,我们称为三角函数,记作
正弦函数
余弦函数
正切函数
四、【 教学过程】——探究新知,形成概念(定义1)
最后给出定义并用数学中函数的符号语言加以表达,完成第三次抽象
例1 求 的正弦、余弦和正切值.
变式1:若把角 改为 呢
四、【 教学过程】——例题学习,理解概念
设计意图:例题先有由学生完成,提供反馈校正的素材,教师及时点评关注学生的数学表达并及时引导学生总结解题步骤,提高总结归纳的能力。通过例题让学生学会根据三角函数的定义求角的三角函数值,及时安排例题,练习源于例题,练习由学生独立完成,加深理解。揭示了教与学的一致性。
四、【 教学过程】——探究新知,形成概念(定义2)
设计意图:通过探究2让学生理解锐角的三角函数与任意角的三角函数的关系。提高学生分析问题的能力。
为了将初中学习的锐角三角函数与本节课三角函数概念统一起来。这里设计了探究2
四、【 教学过程】——例题学习,理解概念(定义2)
设计意图:通过画板演示,学生可以直观感知角的三角函数值不会随点P在终边的位置改变而改变。由于学生基础参差不齐,基础比较好的学生人数很少,因此证明留给有能力的同学下去研究或个别与老师探讨。
师生活动:教师指出例2也是三角函数的另一种定义,并引导学生如何运用第二定义解题。学生自己动手练习,学会运用定义。
由于我们学生数学抽象的素养欠缺,通过探究3让学生直观感知角与三角的函数值的对应关系。
例2:如图,设 是一个任意角,它的终边上任意一点(不与原点重合)的坐标为,点与原点的距离为。求证
探究3:如果改变角的终边上点P的位置,三角函数值是否会改变呢?
设计意图:可多人参与课堂活动,限时的竞争机制更能将学生代入进去,简单的题目设计,激发学生的荣誉感,在活动中学习。
反思评价:这里的竞赛如果选不同小组派代表上台,本组同学可以在台下帮忙回答,这样效果可能会更好,课堂气氛会更加活跃。
四、【 教学过程】——竞赛比拼,深化概念
基于高一学生喜欢挑战的特点,我设计了竞赛比拼的环节
1.填表:求下列特殊角的三角函数值
四、【 教学过程】——当堂练习,巩固概念
2.已知角α终边过点P(1,-1),的值为( )
A.1B.-1C.D.
【解析】由三角函数定义知故选B。
3.在平面直角坐标系xOy中,角α与角β均以Ox为始边,它们的终边关于x轴对称,若sin α=,则sin β=_____.
4.求值:sin 180°+cos 90°+tan 0°
【解析】设角α的终边与单位圆相交于点P(x,y),则角β的终边与单位圆相交于点Q(x,-y),由题意知y=sin α=,所以sin β=-y=-
【解析】sin 180°+cos 90°+tan 0°=0+0+0=0.
设计意图:通过练习巩固本节所学知识,感悟其中蕴含的数学思想,增强学生的应用意识。
四、【 教学过程】——当堂练习,巩固概念
①三角函数的概念.
②三角函数的定义域及三角函数求值.
运用了定义法、公式法、数形结合法解题.
1.通过三角函数的概念,培养数学抽象素养;
2.借助公式的运算,提升数学运算的素养。
四、【 教学过程】——归纳总结,提高认识
设计意图:通过总结,让学生进一步巩固本节所学内容,提高概括能力。
1
2
3
核心素养
使用方法
学习内容
四、【 教学过程】——课后作业,巩固提高
1.已知点在半径为2的圆上按顺时针方向做匀速圆周运动,角速度为.求2时点所在的位置。
设计意图:作业适量,贴合课堂内容,通过作业使学生继续加深对三角函数概念的理解及应用,为后续学习打好基础。通过开放性作业来完善学生对这节课的知识建构体系。
2.开放性作业:用文字、图示等来描述自己对这节课的知识建构情况(知识联系,拓展,框架,结构等)
学 生 练 习 多媒体显示区 学 生 练习1 学生 练习2
例1
反思评价:板书设计不够美观,字体书写还需提升,后续的教学中,会努力改善。
六、【 板书设计】
六、【 教学评价设计】
本节课的指导思想是从发展学生的核心素养出发,以任意角三角函数的概念为载体,让数学抽象的三个阶段真正落地。
以“如何描述周期现象”为出发点,引导学生经历“周期现象—圆周运动—单位圆上点的旋转运动”的学习体验,完成第一次抽象;
让学生完成”给定一个角,求它的终边与单位圆的交点坐标”根据其对应关系,使学生明白三角函数也是函数的过程,完成第二次抽象;
最后给出定义并用数学中函数的符号语言加以表达,完成第三次抽象。
由于函数比较抽象,学生能力不足,教师的讲解偏多.
1
教学反思
六、【 教学评价设计】
教学特色
2
1.学案导学法,能更好的把课堂还给学生。先学后教,学生通过自学及时发现不太清楚的问题,听课时目的性、针对性强,有利于提高听课效率。
2.用希沃白板制作课件,可以设计课堂活动,激发学生的学习兴趣,通过画板演示,学生能够直观的观察 ,更好地理解定义。
感谢
聆听
谢谢大家
5.2.1三角函数的概念
人教2019A版必修 第一册
说课流程
学情分析
教材分析
教法学法分析
教学过程分析
板书设计
教学评价分析
01
02
03
06
05
04
目录
CONTENTS
5.1
任意角和弧度制
三角函数的概念
5.2
4
指数函数
与对数函数
3
函数的概念与性质
3.3幂函数
诱导公式
5.3
三角函数的图像与性质
5.4
5.5
三角恒等变换
承前启后
是学生学习锐角三角函数的进一步扩展,是 本章的基础,对本章的整体学习至关重要。
一、【 教材分析】——教材地位与作用
三角函数
数学必修第一册第五章
一、【 教材分析】——教学目标
借助单位圆理解任意角三角函数的定义;
01
能初步运用定义分析和解决与三角函数值有关的一些简单问题;
02
体验三角函数概念的产生、发展过程,领悟直角坐标系的工具功能,丰富数形结合的经验。
03
数学建模
利用单位圆刻画点的变化情况
数学抽象
三角函数的定义
逻辑推理
三角函数概念的推导过程
数学运算
根据定义求三角函数值
直观想象
三角函数第二定义的推导
一、【 教材分析】——核心素养
重点:
借助单位圆理解任意角三角函数(正弦、余弦、正切)的定义
难点:
1.任意角的三角函数概念的建构过程;
2.角的终边与单位圆的交点坐标。
解决办法:通过复习引入新课,建立知识间的联系,提高学生的抽象概括能力。
一、【 教材分析】——教学重点与难点
1.在初中,学生已学了锐角三角函数。
2. 圆的有关知识。
3.在本章第一节“任意角与弧度制”的内容中学生会用坐标找出任意角与象限角,能够把以前学过的角度在弧度制下表示出来。
学生具备: 学生通过前面函数的学习,已初步具有逻辑思维能力,能在教师的引导下独立解决简单问题。
学生欠缺: 数形结合能力不强,望“函数”而“色变”,数学抽象的素养欠缺
二、【 学情分析】
知识基础
1
2
能力基础
心理特点
高一的学生精力旺盛,好奇心强,喜欢刺激惊险的活动。
3
合作探究
巩固练习
竞赛比拼
三、教法学法分析
基于以上的学情分析,为了突出重点,突破难点,
本节课的教法与学法如下:
三、【 教法学法分析】
问题引领
例题精析
变式练习
学法
学案导学
亲身实践
教法
引导学生主动思考
提高学生合作意识
培养学生规范答题
锻炼学生动手能力
培养自学能力
激发求知欲望
激发学生荣誉感,活动中学习
升华学习内容
四、教学过程分析
另外留1分钟机动
复习旧知,引入新课
(5分钟)
探究新知,形成概念
(15分钟)
例题学习,理解概念(8分钟)
归纳总结,提高认识
(2分钟)
当堂练习,巩固概念
(5分钟)
竞赛比拼,深化概念
(3分钟)
课后作业,巩固提高
(1分钟)
四、【 教学过程分析】
二、课堂教学
一、课前准备
教师准备
学生准备
1、编写学案 2、制作课件 3、多媒体
1、预习教材 2、完成学案相关内容
四、【 教学过程】——复习旧知,引入新课
设计意图:共同回顾,为后面探究任意角的三角函数作了铺垫。
温故知新,让学生体会知识的产生、发展过程。
由于学生的基础比较差,前面学过的知识容易遗忘,我采用复习旧知的方式,引入新课
四、【 教学过程】——探究新知,形成概念(定义1)
设计意图:通过问题1,引导学生建立坐标系,求点P的坐标,为探究1做准备。
为了完成函数的第一次抽象,我设计了问题1
四、【 教学过程】——探究新知,形成概念(定义1)
设计意图:通过分组探究、教师指导的形式,让学生能求角的终边与单位圆的交点坐标,进而明白其确定性。并突破本节课的难点2。通过问题2,即体现了由特殊到一般的特点,同时为三角函数的概念起着铺垫的作用。
问题2:一般地,任意给定一个角 ,它的终边OP与单位圆交点P的坐标能唯一确定吗?
为完成函数概念的第二次抽象,设计了探究1
学生活动:小组探究,派代表上黑板板书探究的结果。
四、【 教学过程】——探究新知,形成概念(定义1)
设计意图:在这里及时讨论函数的定义域,更直观,学生更容易理解,特别是正切函数的定义域一目了然。
通过探究1,得出三角函数的定义,学习了函数就要研究函数的定义域,下面通过小组讨论完成这一任务。
正弦函数、余弦函数、正切函数都是以角为自变量,以单位圆上点的坐标或坐标的比值为函数值的函数,我们称为三角函数,记作
正弦函数
余弦函数
正切函数
四、【 教学过程】——探究新知,形成概念(定义1)
最后给出定义并用数学中函数的符号语言加以表达,完成第三次抽象
例1 求 的正弦、余弦和正切值.
变式1:若把角 改为 呢
四、【 教学过程】——例题学习,理解概念
设计意图:例题先有由学生完成,提供反馈校正的素材,教师及时点评关注学生的数学表达并及时引导学生总结解题步骤,提高总结归纳的能力。通过例题让学生学会根据三角函数的定义求角的三角函数值,及时安排例题,练习源于例题,练习由学生独立完成,加深理解。揭示了教与学的一致性。
四、【 教学过程】——探究新知,形成概念(定义2)
设计意图:通过探究2让学生理解锐角的三角函数与任意角的三角函数的关系。提高学生分析问题的能力。
为了将初中学习的锐角三角函数与本节课三角函数概念统一起来。这里设计了探究2
四、【 教学过程】——例题学习,理解概念(定义2)
设计意图:通过画板演示,学生可以直观感知角的三角函数值不会随点P在终边的位置改变而改变。由于学生基础参差不齐,基础比较好的学生人数很少,因此证明留给有能力的同学下去研究或个别与老师探讨。
师生活动:教师指出例2也是三角函数的另一种定义,并引导学生如何运用第二定义解题。学生自己动手练习,学会运用定义。
由于我们学生数学抽象的素养欠缺,通过探究3让学生直观感知角与三角的函数值的对应关系。
例2:如图,设 是一个任意角,它的终边上任意一点(不与原点重合)的坐标为,点与原点的距离为。求证
探究3:如果改变角的终边上点P的位置,三角函数值是否会改变呢?
设计意图:可多人参与课堂活动,限时的竞争机制更能将学生代入进去,简单的题目设计,激发学生的荣誉感,在活动中学习。
反思评价:这里的竞赛如果选不同小组派代表上台,本组同学可以在台下帮忙回答,这样效果可能会更好,课堂气氛会更加活跃。
四、【 教学过程】——竞赛比拼,深化概念
基于高一学生喜欢挑战的特点,我设计了竞赛比拼的环节
1.填表:求下列特殊角的三角函数值
四、【 教学过程】——当堂练习,巩固概念
2.已知角α终边过点P(1,-1),的值为( )
A.1B.-1C.D.
【解析】由三角函数定义知故选B。
3.在平面直角坐标系xOy中,角α与角β均以Ox为始边,它们的终边关于x轴对称,若sin α=,则sin β=_____.
4.求值:sin 180°+cos 90°+tan 0°
【解析】设角α的终边与单位圆相交于点P(x,y),则角β的终边与单位圆相交于点Q(x,-y),由题意知y=sin α=,所以sin β=-y=-
【解析】sin 180°+cos 90°+tan 0°=0+0+0=0.
设计意图:通过练习巩固本节所学知识,感悟其中蕴含的数学思想,增强学生的应用意识。
四、【 教学过程】——当堂练习,巩固概念
①三角函数的概念.
②三角函数的定义域及三角函数求值.
运用了定义法、公式法、数形结合法解题.
1.通过三角函数的概念,培养数学抽象素养;
2.借助公式的运算,提升数学运算的素养。
四、【 教学过程】——归纳总结,提高认识
设计意图:通过总结,让学生进一步巩固本节所学内容,提高概括能力。
1
2
3
核心素养
使用方法
学习内容
四、【 教学过程】——课后作业,巩固提高
1.已知点在半径为2的圆上按顺时针方向做匀速圆周运动,角速度为.求2时点所在的位置。
设计意图:作业适量,贴合课堂内容,通过作业使学生继续加深对三角函数概念的理解及应用,为后续学习打好基础。通过开放性作业来完善学生对这节课的知识建构体系。
2.开放性作业:用文字、图示等来描述自己对这节课的知识建构情况(知识联系,拓展,框架,结构等)
学 生 练 习 多媒体显示区 学 生 练习1 学生 练习2
例1
反思评价:板书设计不够美观,字体书写还需提升,后续的教学中,会努力改善。
六、【 板书设计】
六、【 教学评价设计】
本节课的指导思想是从发展学生的核心素养出发,以任意角三角函数的概念为载体,让数学抽象的三个阶段真正落地。
以“如何描述周期现象”为出发点,引导学生经历“周期现象—圆周运动—单位圆上点的旋转运动”的学习体验,完成第一次抽象;
让学生完成”给定一个角,求它的终边与单位圆的交点坐标”根据其对应关系,使学生明白三角函数也是函数的过程,完成第二次抽象;
最后给出定义并用数学中函数的符号语言加以表达,完成第三次抽象。
由于函数比较抽象,学生能力不足,教师的讲解偏多.
1
教学反思
六、【 教学评价设计】
教学特色
2
1.学案导学法,能更好的把课堂还给学生。先学后教,学生通过自学及时发现不太清楚的问题,听课时目的性、针对性强,有利于提高听课效率。
2.用希沃白板制作课件,可以设计课堂活动,激发学生的学习兴趣,通过画板演示,学生能够直观的观察 ,更好地理解定义。
感谢
聆听
谢谢大家
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
