21.2 二次函数的图象和性质(9)课件(共29张PPT)
文档属性
| 名称 | 21.2 二次函数的图象和性质(9)课件(共29张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-25 00:00:00 | ||
图片预览






文档简介
(共29张PPT)
沪科版 九年级上册
21.2二次函数的图象和性质(9)
已知一次函数图象上两点(两点的连线不与坐标轴平行)的坐标,可以确定一次函数解析式,同样二次函数也可以通过图象上已知点的坐标来确定解析式.本节课要研究的就是通过图象上已知点,来确定二次函数解析式.主要是通过三点确定一般式.
课件说明
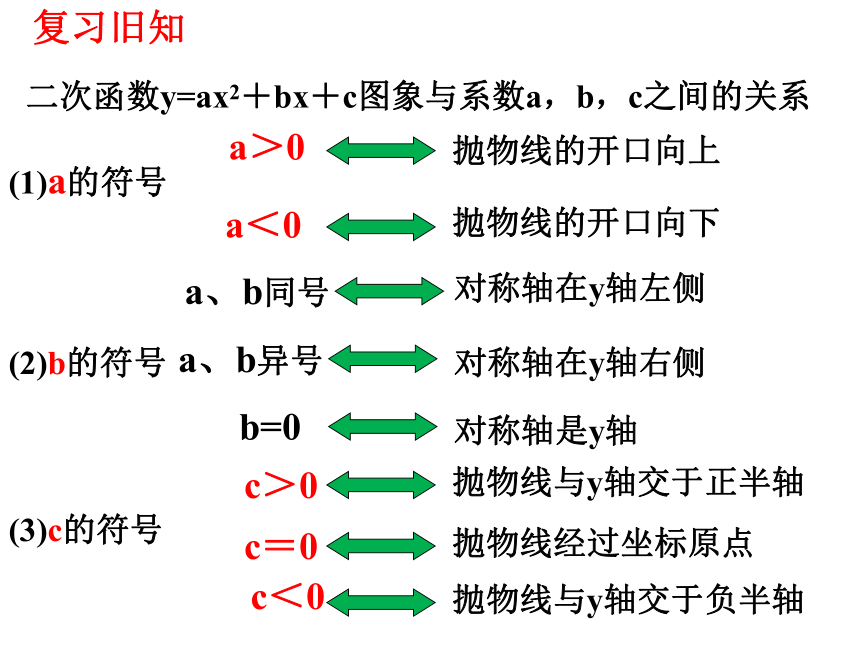
二次函数y=ax2+bx+c图象与系数a,b,c之间的关系
(1)a的符号
抛物线的开口向上
a>0
抛物线的开口向下
a<0
对称轴在y轴左侧
a、b同号
对称轴在y轴右侧
a、b异号
对称轴是y轴
b=0
抛物线与y轴交于正半轴
c>0
c<0
抛物线经过坐标原点
c=0
抛物线与y轴交于负半轴
(3)c的符号
(2)b的符号
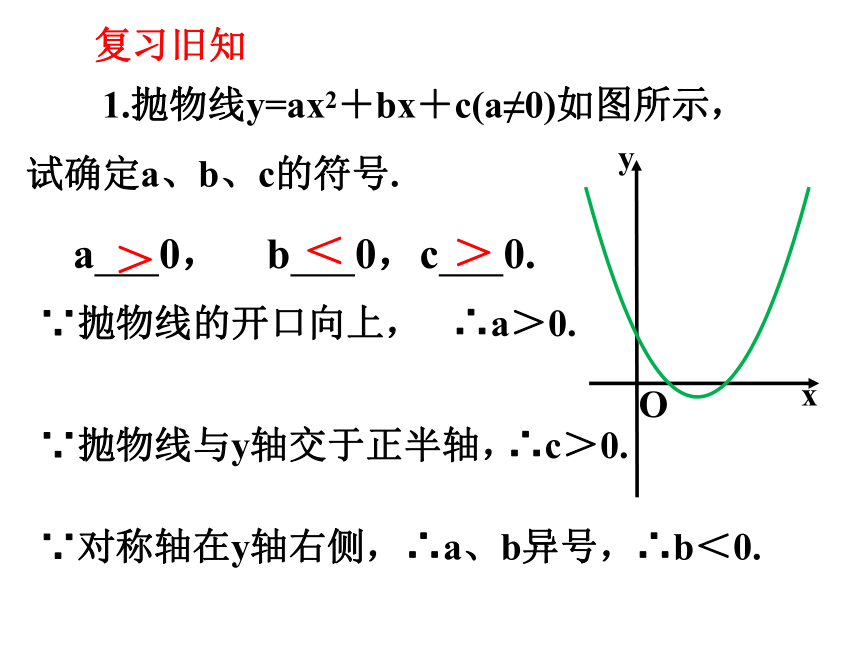
复习旧知
∵抛物线与y轴交于正半轴,
1.抛物线y=ax2+bx+c(a≠0)如图所示,
试确定a、b、c的符号.
x
y
O
a 0, b 0,c 0.
>
<
>
∴a>0.
∵抛物线的开口向上,
∴c>0.
∵对称轴在y轴右侧,
∴b<0.
∴a、b异号,
复习旧知
2.抛物线y=ax2+bx+c(a≠0)如图所示,试
判断下来字母和代数式的符号.
a 0, b 0, c 0.
x
y
O
1
2
-1
a+b+c 0, a-b+c 0.
<
>
>
>
<
3.写出下列抛物线的开口方向,对称轴和顶点坐标.
(1) y =2x2+8x-6;
(2) y =- x2-2x-1.
1
2
开口方向 对称轴 顶点坐标
向上
x=
向下
x=-2
( , )
(-2,1)
-2
-14
-2
b=8,
x =
b
2a
-
=
8
2×2
-
=-2,
∵a=2>0,
b=-2,
x =
b
2a
-
=
-2
2×(- )
-
∵a=- <0,
1
2
1
2
=-2,
已知一次函数y=kx+b图象上的几个点可以求出它的解析式?利用了怎样的方法?
已知一次函数图象上的两个点可以求出它的解析式.
利用待定系数方法.
列出关于k、b的二元一次方程组,
求出k、b的值.
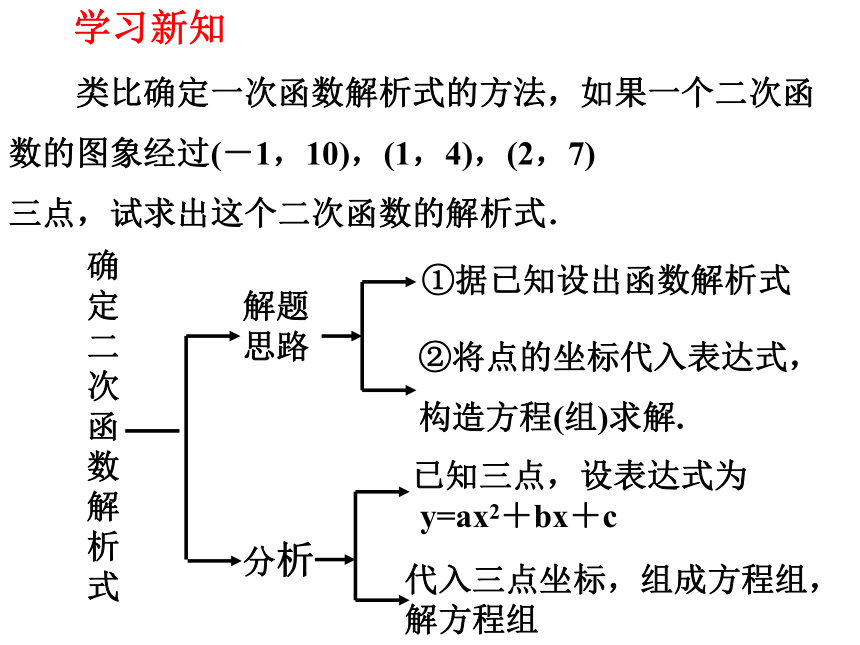
引入新知
类比确定一次函数解析式的方法,如果一个二次函数的图象经过(-1,10),(1,4),(2,7)
三点,试求出这个二次函数的解析式.
学习新知
确定二次函数解析式
解题思路
分析
①据已知设出函数解析式
②将点的坐标代入表达式,
构造方程(组)求解.
已知三点,设表达式为
y=ax2+bx+c
代入三点坐标,组成方程组,
解方程组
一个二次函数的图象经过(-1,10),(1,4),(2,7)
三点,试求出这个二次函数的解析式.
设所求二次函数为 y=ax2+bx+c.
解:
由函数图象经过(-1,10),(1,4),(2,7)三点,得关于 a,b,c 的三元一次方程组
a+b+c = 4
a-b+c = 10
4a+2b+c = 7
①
②
③
例题解析
如何解这个方程组?
a+b+c = 4
a-b+c = 10
4a+2b+c = 7
①
②
③
②
-
①
2b= -6
b= -3
-
①
③
3a+3b =-3
a+b =-1
a=2
2-3+c = 4
c = 5
一个二次函数的图象经过(-1,10),(1,4),(2,7)
三点,试求出这个二次函数的解析式.
设所求二次函数为 y=ax2+bx+c.
解:
由函数图象经过(-1,10),(1,4),(2,7)三点,
得关于 a,b,c 的三元一次方程组
a+b+c = 4
a-b+c = 10
4a+2b+c = 7
解这个方程组,得
a = 2,b = -3,c = 5.
所求的二次函数是 y = 2x2-3x+5.
1. 一个二次函数,当自变量x=0时,函数值y=-1,
当x=-2与 是,y=0. 求这个二次函数的解析式.
设所求二次函数为 y=ax2+bx+c.
解:
c =- 1
4a-2b+c = 0
a+ b+c =0
1
2
1
2
1
4
根据题意,得
学以致用
如何解这个方程组?
c =- 1
4a-2b+c = 0
a+ b+c =0
1
2
1
4
3
2
①
②
③
由③得
a+ 2b+4c =0
④
④
②
+
5a+5c =0
a+c =0
∴a=1,
b=
1.一个二次函数,当自变量x=0时,函数值y=-1,
当x=-2与 是,y=0. 求这个二次函数的解析式.
设所求二次函数为 y=ax2+bx+c.
解:
c =- 1
4a-2b+c = 0
a+ b+c =0
解这个方程组,得
a = 1,b = ,c = -1.
所求的二次函数解析式是 y = x2+ x-1.
1
2
1
2
1
4
根据题意,得
3
2
3
2
2.一个二次函数的图象经过(0,0),(-1,-11),
(1,9)三点,试求出这个二次函数的解析式.
设所求二次函数为 y=ax2+bx+c.
解:
由函数图象经过(0,0),(-1,-11) ,(1,9)三点,得关于 a,b,c 的三元一次方程组
c = 0
a-b+c = -11
a+b+c = 9
解这个方程组,得
a =-1,b = 10,c = 0.
所求的二次函数解析式是 y = -x2 +10x.
设所求二次函数为 y = ax2+bx+c.
解:
由函数图象经过点(1,-4),(2,-3),
得关于 a,b,c 的三元一次方程组
a+b+c =-4
4a+2b+c =-3
①
②
③
3.一个二次函数图象的顶点为(1,-4),图象又过点(2,-3),求这个二次函数的解析式.
b
2a
-
=1
a+b+c =-4
4a+2b+c =-3
①
②
③
b
2a
-
=1
②
-
①
3a+b =1
由③得
b=-2a
④
⑤
将⑤代入④,
解得a=1,
∴b=-2,
∴c =-3
所求的二次函数解析式是 y = x2-2x-3.
3.一个二次函数图象的顶点为(1,-4),图象又过点(2,-3),求这个二次函数的解析式.
y=a(x+h) 2+k.
∴y=a(x-1) 2-4.
∴a(2-1) 2-4=-3,
y=(x-1)2-4.
即y=x2-2x -3
解法2
用顶点式作题设
解:设所求二次函数解析式为
∵图象的顶点为(1,-4),
∴-h =1, k =-4.
∵函数图象经过点(2,-3),
∴a = 1.
∴所求的二次函数解析式是
二次函数表达式类型
(1)一般形式:
y=ax2+bx+c(a ≠ 0),
(2)顶点形式:
y=a(x+h) 2+k (a ≠ 0),
(3)交点形式:
y=a(x-x1)(x-x2) (a ≠ 0),
②列方程(组)
①设适当表达式
④写出表达式
二次函数表达式的确定
③解方程(组)
二次函数表达式确定步骤
在设函数的表达式时,一定要根据题中所给条件选择的形式:
①当已知抛物线上的三点坐标时,可设函数的
表达 y=ax2+bx+c;
②当已知抛物线的顶点坐标或对称轴或最大最小值时,
可设函数的表达式为y=a(x-h)2+k;
③当已知抛线与x轴的两个交点(x1,0),(x2,0)时,
可设函数的表达式 y=a(x-x1)(x-x2).
(1)本节课学了哪些主要内容?
(2)确定解析式的关键是什么?
课堂小结
1.已知二次函数y=ax +bx,当x=1时,y=2;
当x=-1时, y=4.则此二次函数的表达式是( ).
A.y=3x +x B.y=-3x +x
C.y=-3x -x
D.y=3x -x
D
2.已知抛物线经过A(0,0),B(- 1,0),C(1,2)
三点,则抛物线的函数表达式是( ).
A. y=-x +x2 B.y=-x +2x+1
C .y=-x +x D.y=x +x
3.已知抛物线的顶点坐标是(2,4),且经过点
(3,7),则抛物线的函数表达式( ).
A. y=3x -12x+16 B.y=-3x +12x+16
C .y=-3x +12x-16 D.y=3x +12x-16
D
A
4.已知二次函数的图象如图,则这个二次函数
的表达式为( ).
A. y=x -2x+3 B.y=x -2x-3
C. y=x +2x+3 D.y=x +2x-3
B
5.若抛物线y=-x -2x+c与y轴交于点(0,3),
则下列说法不正确的是( ).
A.抛物线开口向下
B.抛物线的对称轴是直线x=-1
C.当x=-1时,y取得最小值4
D.抛物线经过点(1,0)
C
6.在同一平面直角坐标系中,函数y=x2+a与
y=ax+1的图象可能是( ).
A. B.
C. D.
x
y
O
x
y
O
x
y
O
x
y
O
C
今天作业
课本P27页第9题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 九年级上册
21.2二次函数的图象和性质(9)
已知一次函数图象上两点(两点的连线不与坐标轴平行)的坐标,可以确定一次函数解析式,同样二次函数也可以通过图象上已知点的坐标来确定解析式.本节课要研究的就是通过图象上已知点,来确定二次函数解析式.主要是通过三点确定一般式.
课件说明
二次函数y=ax2+bx+c图象与系数a,b,c之间的关系
(1)a的符号
抛物线的开口向上
a>0
抛物线的开口向下
a<0
对称轴在y轴左侧
a、b同号
对称轴在y轴右侧
a、b异号
对称轴是y轴
b=0
抛物线与y轴交于正半轴
c>0
c<0
抛物线经过坐标原点
c=0
抛物线与y轴交于负半轴
(3)c的符号
(2)b的符号
复习旧知
∵抛物线与y轴交于正半轴,
1.抛物线y=ax2+bx+c(a≠0)如图所示,
试确定a、b、c的符号.
x
y
O
a 0, b 0,c 0.
>
<
>
∴a>0.
∵抛物线的开口向上,
∴c>0.
∵对称轴在y轴右侧,
∴b<0.
∴a、b异号,
复习旧知
2.抛物线y=ax2+bx+c(a≠0)如图所示,试
判断下来字母和代数式的符号.
a 0, b 0, c 0.
x
y
O
1
2
-1
a+b+c 0, a-b+c 0.
<
>
>
>
<
3.写出下列抛物线的开口方向,对称轴和顶点坐标.
(1) y =2x2+8x-6;
(2) y =- x2-2x-1.
1
2
开口方向 对称轴 顶点坐标
向上
x=
向下
x=-2
( , )
(-2,1)
-2
-14
-2
b=8,
x =
b
2a
-
=
8
2×2
-
=-2,
∵a=2>0,
b=-2,
x =
b
2a
-
=
-2
2×(- )
-
∵a=- <0,
1
2
1
2
=-2,
已知一次函数y=kx+b图象上的几个点可以求出它的解析式?利用了怎样的方法?
已知一次函数图象上的两个点可以求出它的解析式.
利用待定系数方法.
列出关于k、b的二元一次方程组,
求出k、b的值.
引入新知
类比确定一次函数解析式的方法,如果一个二次函数的图象经过(-1,10),(1,4),(2,7)
三点,试求出这个二次函数的解析式.
学习新知
确定二次函数解析式
解题思路
分析
①据已知设出函数解析式
②将点的坐标代入表达式,
构造方程(组)求解.
已知三点,设表达式为
y=ax2+bx+c
代入三点坐标,组成方程组,
解方程组
一个二次函数的图象经过(-1,10),(1,4),(2,7)
三点,试求出这个二次函数的解析式.
设所求二次函数为 y=ax2+bx+c.
解:
由函数图象经过(-1,10),(1,4),(2,7)三点,得关于 a,b,c 的三元一次方程组
a+b+c = 4
a-b+c = 10
4a+2b+c = 7
①
②
③
例题解析
如何解这个方程组?
a+b+c = 4
a-b+c = 10
4a+2b+c = 7
①
②
③
②
-
①
2b= -6
b= -3
-
①
③
3a+3b =-3
a+b =-1
a=2
2-3+c = 4
c = 5
一个二次函数的图象经过(-1,10),(1,4),(2,7)
三点,试求出这个二次函数的解析式.
设所求二次函数为 y=ax2+bx+c.
解:
由函数图象经过(-1,10),(1,4),(2,7)三点,
得关于 a,b,c 的三元一次方程组
a+b+c = 4
a-b+c = 10
4a+2b+c = 7
解这个方程组,得
a = 2,b = -3,c = 5.
所求的二次函数是 y = 2x2-3x+5.
1. 一个二次函数,当自变量x=0时,函数值y=-1,
当x=-2与 是,y=0. 求这个二次函数的解析式.
设所求二次函数为 y=ax2+bx+c.
解:
c =- 1
4a-2b+c = 0
a+ b+c =0
1
2
1
2
1
4
根据题意,得
学以致用
如何解这个方程组?
c =- 1
4a-2b+c = 0
a+ b+c =0
1
2
1
4
3
2
①
②
③
由③得
a+ 2b+4c =0
④
④
②
+
5a+5c =0
a+c =0
∴a=1,
b=
1.一个二次函数,当自变量x=0时,函数值y=-1,
当x=-2与 是,y=0. 求这个二次函数的解析式.
设所求二次函数为 y=ax2+bx+c.
解:
c =- 1
4a-2b+c = 0
a+ b+c =0
解这个方程组,得
a = 1,b = ,c = -1.
所求的二次函数解析式是 y = x2+ x-1.
1
2
1
2
1
4
根据题意,得
3
2
3
2
2.一个二次函数的图象经过(0,0),(-1,-11),
(1,9)三点,试求出这个二次函数的解析式.
设所求二次函数为 y=ax2+bx+c.
解:
由函数图象经过(0,0),(-1,-11) ,(1,9)三点,得关于 a,b,c 的三元一次方程组
c = 0
a-b+c = -11
a+b+c = 9
解这个方程组,得
a =-1,b = 10,c = 0.
所求的二次函数解析式是 y = -x2 +10x.
设所求二次函数为 y = ax2+bx+c.
解:
由函数图象经过点(1,-4),(2,-3),
得关于 a,b,c 的三元一次方程组
a+b+c =-4
4a+2b+c =-3
①
②
③
3.一个二次函数图象的顶点为(1,-4),图象又过点(2,-3),求这个二次函数的解析式.
b
2a
-
=1
a+b+c =-4
4a+2b+c =-3
①
②
③
b
2a
-
=1
②
-
①
3a+b =1
由③得
b=-2a
④
⑤
将⑤代入④,
解得a=1,
∴b=-2,
∴c =-3
所求的二次函数解析式是 y = x2-2x-3.
3.一个二次函数图象的顶点为(1,-4),图象又过点(2,-3),求这个二次函数的解析式.
y=a(x+h) 2+k.
∴y=a(x-1) 2-4.
∴a(2-1) 2-4=-3,
y=(x-1)2-4.
即y=x2-2x -3
解法2
用顶点式作题设
解:设所求二次函数解析式为
∵图象的顶点为(1,-4),
∴-h =1, k =-4.
∵函数图象经过点(2,-3),
∴a = 1.
∴所求的二次函数解析式是
二次函数表达式类型
(1)一般形式:
y=ax2+bx+c(a ≠ 0),
(2)顶点形式:
y=a(x+h) 2+k (a ≠ 0),
(3)交点形式:
y=a(x-x1)(x-x2) (a ≠ 0),
②列方程(组)
①设适当表达式
④写出表达式
二次函数表达式的确定
③解方程(组)
二次函数表达式确定步骤
在设函数的表达式时,一定要根据题中所给条件选择的形式:
①当已知抛物线上的三点坐标时,可设函数的
表达 y=ax2+bx+c;
②当已知抛物线的顶点坐标或对称轴或最大最小值时,
可设函数的表达式为y=a(x-h)2+k;
③当已知抛线与x轴的两个交点(x1,0),(x2,0)时,
可设函数的表达式 y=a(x-x1)(x-x2).
(1)本节课学了哪些主要内容?
(2)确定解析式的关键是什么?
课堂小结
1.已知二次函数y=ax +bx,当x=1时,y=2;
当x=-1时, y=4.则此二次函数的表达式是( ).
A.y=3x +x B.y=-3x +x
C.y=-3x -x
D.y=3x -x
D
2.已知抛物线经过A(0,0),B(- 1,0),C(1,2)
三点,则抛物线的函数表达式是( ).
A. y=-x +x2 B.y=-x +2x+1
C .y=-x +x D.y=x +x
3.已知抛物线的顶点坐标是(2,4),且经过点
(3,7),则抛物线的函数表达式( ).
A. y=3x -12x+16 B.y=-3x +12x+16
C .y=-3x +12x-16 D.y=3x +12x-16
D
A
4.已知二次函数的图象如图,则这个二次函数
的表达式为( ).
A. y=x -2x+3 B.y=x -2x-3
C. y=x +2x+3 D.y=x +2x-3
B
5.若抛物线y=-x -2x+c与y轴交于点(0,3),
则下列说法不正确的是( ).
A.抛物线开口向下
B.抛物线的对称轴是直线x=-1
C.当x=-1时,y取得最小值4
D.抛物线经过点(1,0)
C
6.在同一平面直角坐标系中,函数y=x2+a与
y=ax+1的图象可能是( ).
A. B.
C. D.
x
y
O
x
y
O
x
y
O
x
y
O
C
今天作业
课本P27页第9题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
