21.2 二次函数的图象和性质(10)课件(共30张PPT)
文档属性
| 名称 | 21.2 二次函数的图象和性质(10)课件(共30张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-25 00:00:00 | ||
图片预览




文档简介
(共30张PPT)
沪科版 九年级上册
21.2二次函数的图象和性质(10)
本节课主要是通过例5的学习,学习求抛物线三角形面积(三角形的顶点都在抛物线上)的方法.体会解决问题的转化思想方法.
课件说明
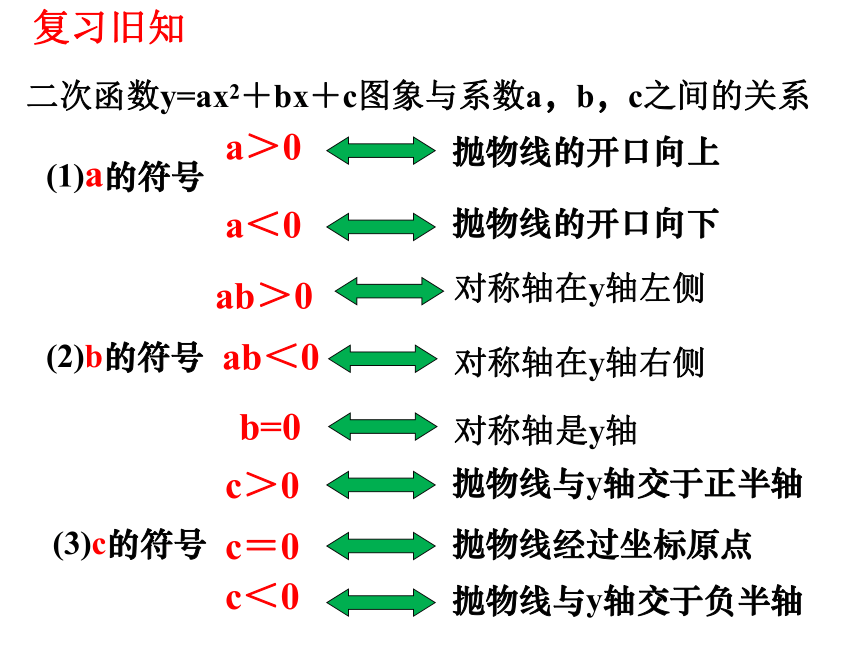
二次函数y=ax2+bx+c图象与系数a,b,c之间的关系
(1)a的符号
抛物线的开口向上
a>0
抛物线的开口向下
a<0
对称轴在y轴左侧
ab>0
对称轴在y轴右侧
ab<0
对称轴是y轴
b=0
抛物线与y轴交于正半轴
c>0
c<0
抛物线经过坐标原点
c=0
抛物线与y轴交于负半轴
(3)c的符号
(2)b的符号
复习旧知
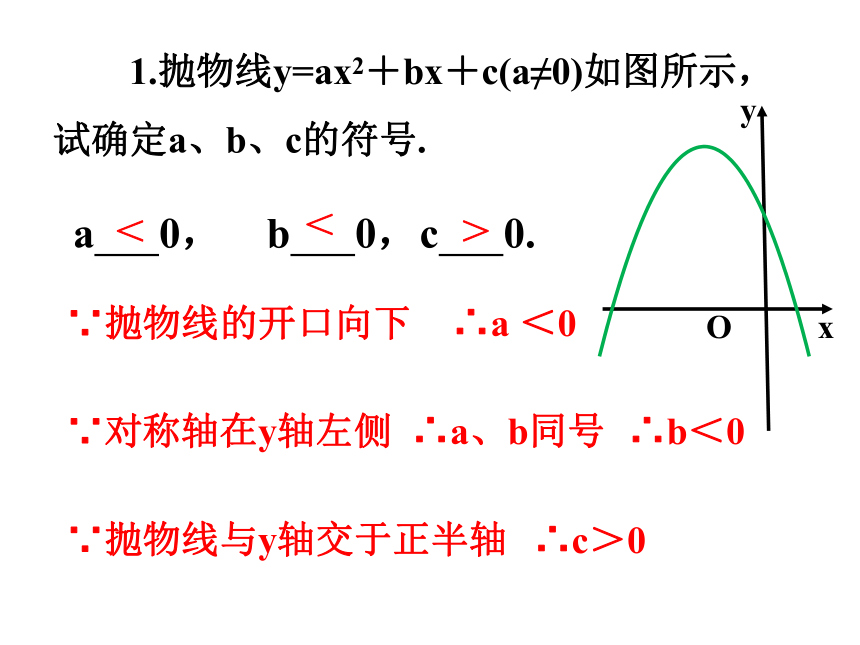
1.抛物线y=ax2+bx+c(a≠0)如图所示,
试确定a、b、c的符号.
x
y
O
a 0, b 0,c 0.
<
<
>
∴a <0
∵抛物线的开口向下
∴c>0
∵抛物线与y轴交于正半轴
∵对称轴在y轴左侧
∴b<0
∴a、b同号
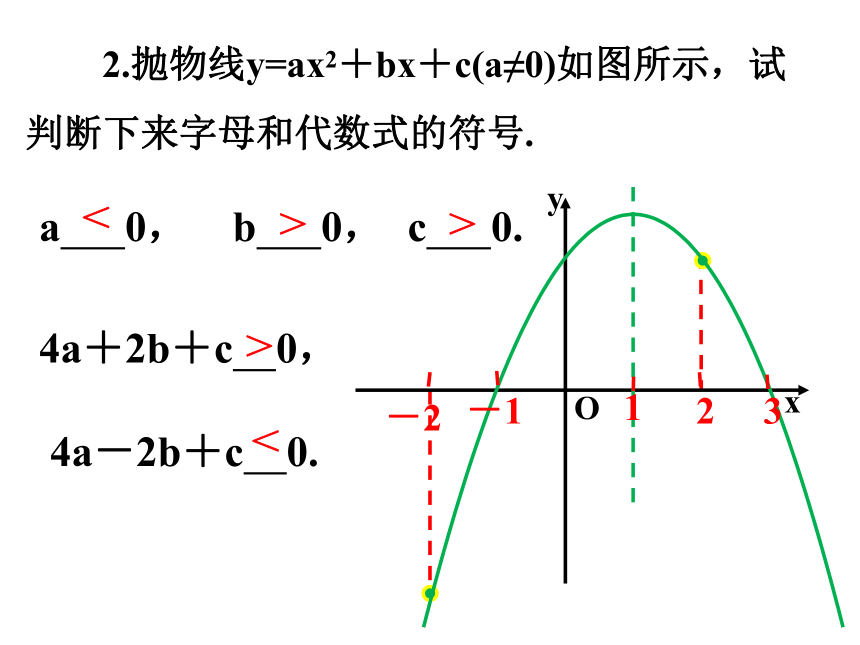
2.抛物线y=ax2+bx+c(a≠0)如图所示,试
判断下来字母和代数式的符号.
a 0, b 0, c 0.
4a+2b+c 0,
4a-2b+c 0.
<
>
>
>
<
x
y
O
1
2
-1
-2
3
例5 抛物线 与直线 交于B,C两点.
y = x2-4x+8
1
2
y = x+1
1
2
(1)在同一平面直角坐标系中画出直线与抛物线;
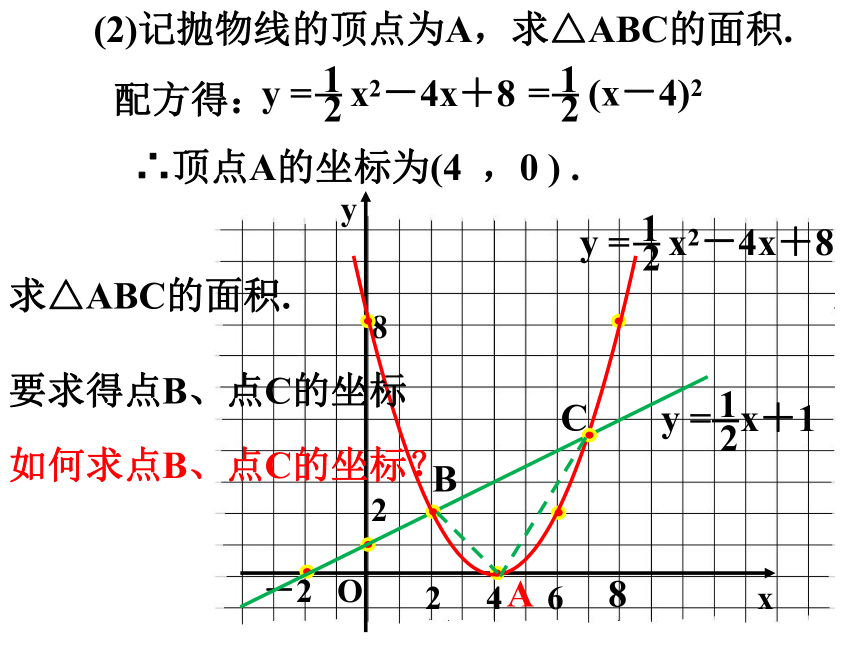
(2)记抛物线的顶点为A,求△ABC的面积.
学习新知
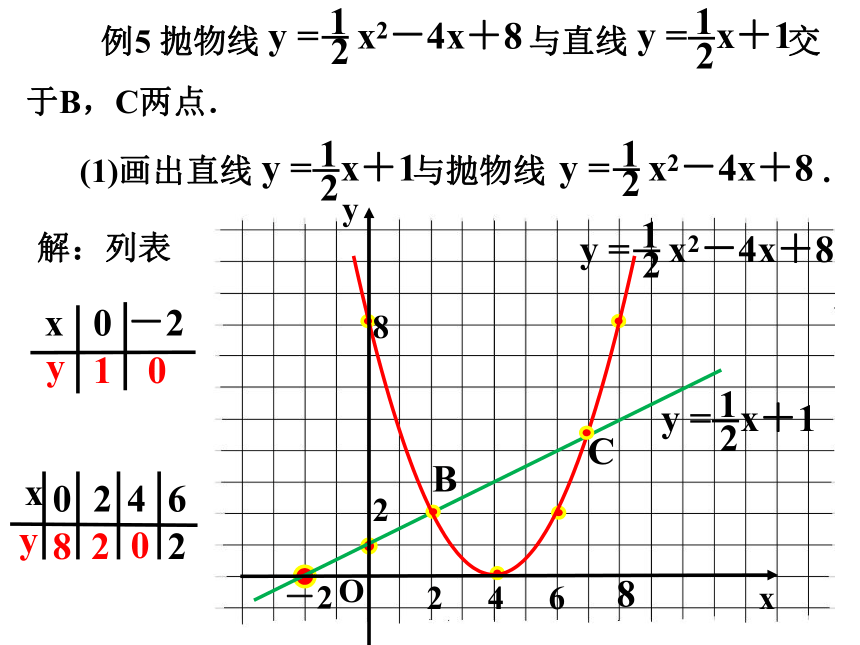
例5 抛物线 与直线 交于B,C两点.
y = x2-4x+8
1
2
y = x+1
1
2
(1)画出直线 与抛物线 .
解:列表
y = x+1
1
2
y = x2-4x+8
1
2
-2
y
x
0
1
0
-2
y = x+1
1
2
y = x2-4x+8
1
2
B
C
2
6
4
8
2
O
x
y
8
y
x
0
8
2
2
4
0
6
2
2
6
4
8
2
O
x
y
-2
y = x+1
1
2
y = x2-4x+8
1
2
B
C
(2)记抛物线的顶点为A,求△ABC的面积.
8
y = x2-4x+8
1
2
= (x-4)2
1
2
配方得:
∴顶点A的坐标为(4 ,0 ) .
A
求△ABC的面积.
要求得点B、点C的坐标
如何求点B、点C的坐标?
2
6
4
8
2
O
x
y
-2
y = x+1
1
2
y = x2-4x+8
1
2
B
C
8
y = x2-4x+8
1
2
解方程组
A
y = x+1
1
2
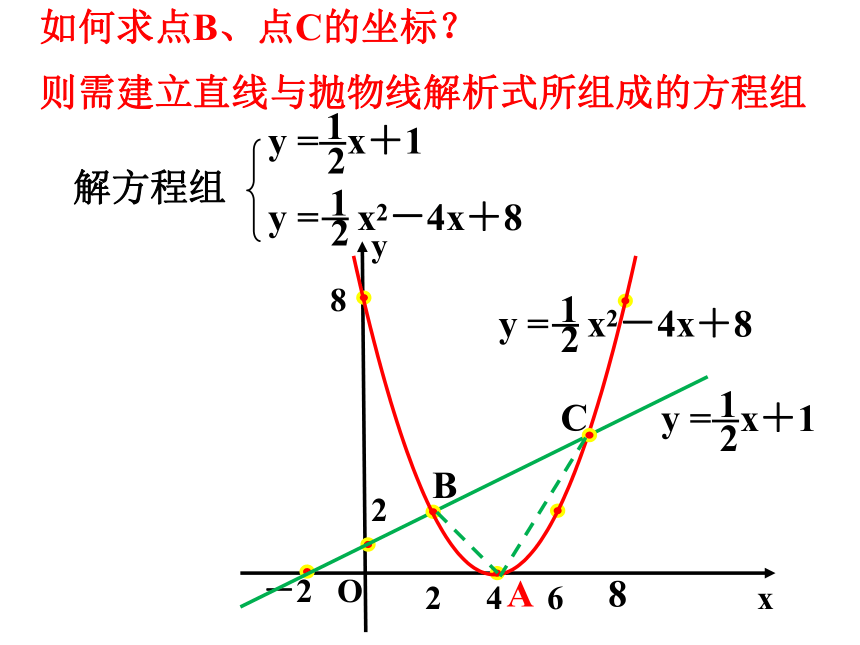
如何求点B、点C的坐标?
则需建立直线与抛物线解析式所组成的方程组
y = x2-4x+8
1
2
y = x+1
1
2
解方程组
= x+1
1
2
x2-4x+8
1
2
x2-8x+16=
x+2
x2-9x+14=0
(x-2)(x-7)=0
∴x1=2,
x2=7
y1=2,
y2=4.5
①
②
分别代入①,得
x1=2,
y1=2
x2=7,
y2=4.5.
∴点B的坐标为(2,2)、点C坐标为(7,4.5).
-2
B
C
7
1
4
2
1
O
x
y
y = x+1
1
2
y = x2-4x+8
1
2
A
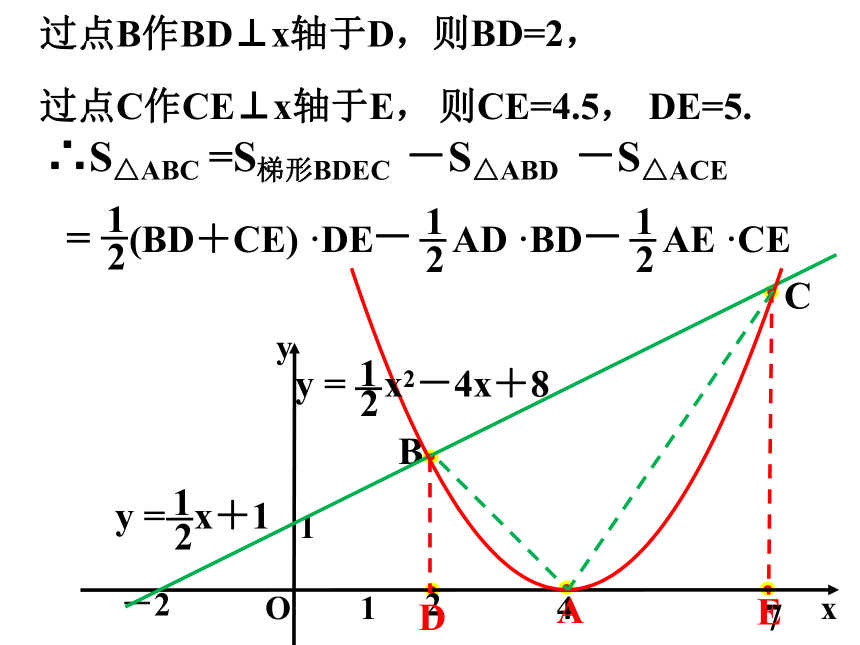
过点B作BD⊥x轴于D,
过点C作CE⊥x轴于E,
则BD=2,
则CE=4.5,
∴S△ABC
-S△ABD
-S△ACE
=S梯形BDEC
= (BD+CE) ·DE
- AD ·BD
- AE ·CE
1
2
1
2
1
2
DE=5.
D
E
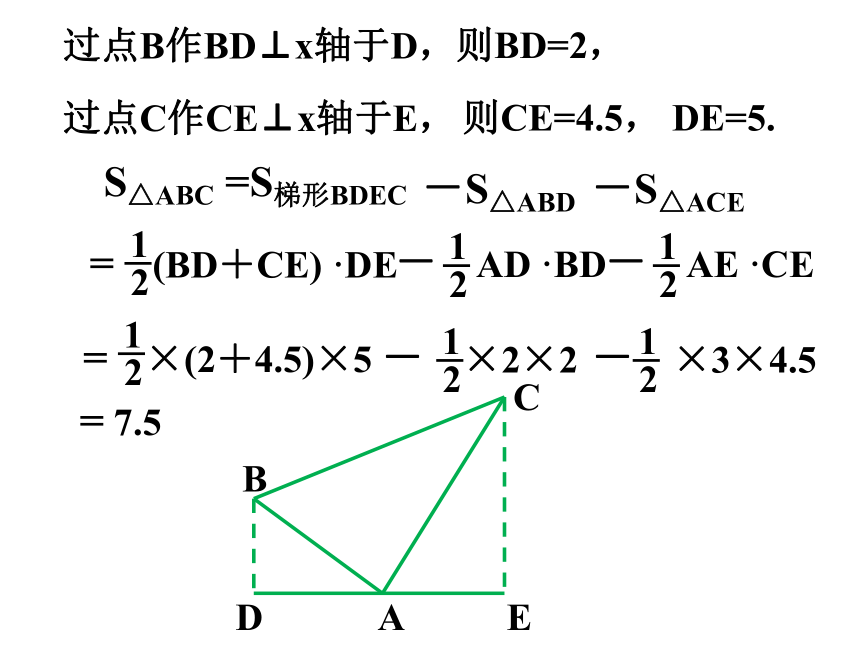
过点B作BD⊥x轴于D,
过点C作CE⊥x轴于E,
则BD=2,
则CE=4.5,
S△ABC
-S△ABD
-S△ACE
=S梯形BDEC
= (BD+CE) ·DE
- AD ·BD
- AE ·CE
1
2
1
2
1
2
= ×(2+4.5)×5
1
2
- ×2×2
- ×3×4.5
1
2
1
2
DE=5.
= 7.5
B
D
E
C
A
-2
B
C
7
1
4
2
1
O
x
y
y = x+1
1
2
y = x2-4x+8
1
2
A
过点B作BD⊥x轴于D,
过点C作CE⊥x轴于E,
则BD=2,
则CE=4.5,
S△ABC
-S△ABD
-S△ACE
=S梯形BDEC
= (BD+CE) ·DE
- AD ·BD
- AE ·CE
1
2
1
2
1
2
= ×(2+4.5)×5
1
2
- ×2×2
- ×3×4.5
1
2
1
2
DE=5.
= 7.5
D
E
2
6
4
2
O
x
y
-2
B
C
8
y = x2-4x+8
1
2
解方程组
A
y = x+1
1
2
x1=2
y1=2,
x2=7
y2=4.5.
得
∴点B的坐标为(2 ,2 ),
点C的坐标为(7 ,4.5 ).
D
E
过点B作BD⊥x轴于D,
过点C作CE⊥x轴于E,
则BD=2,
则CE=4.5.
DE=5.
S△ABC
-S△ABD
-S△ACE
=S梯形BDEC
= (BD+CE) ·DE
- AD ·BD
- AE ·CE
1
2
1
2
1
2
= ×(2+4.5)×5
1
2
- ×2×2
- ×3×4.5
1
2
1
2
= 7.5
4
2
2
O
x
y
-2
y = x+1
1
2
y = x2-4x+8
1
2
B
C
7
A
D
过点A作AD⊥x轴交直线BC于D,
则AD=3,
(4 , 3) .
解法2
铅垂法
过函数图象上的点作坐标轴的垂线的方法
则点D的横坐标为4,
∵点D在直线BC上,
∴点D的纵坐标为3.
4
2
2
O
x
y
-2
y = x+1
1
2
y = x2-4x+8
1
2
B
C
7
A
D
E
F
过点A作AD⊥x轴交直线BC于D,
则AD=3,
过点B作BE⊥AD于E,
则BE=2,
过点C作CF⊥AD交AD的延长线于F,
则CF=3.
S△ABC=
S△ABD
+S△ACD
=
AD ·BE
+ AD ·CF
1
2
1
2
(4 , 3) .
过点A作AD⊥x轴交直线BC于D,
则AD=3,
过点B作BE⊥AD于E,
则BE=2,
过点C作CF⊥AD交AD的延长线于F,
则CF=3.
S△ABC=
S△ABD
+S△ACD
=
AD ·BE
+ AD ·CF
1
2
1
2
=
AD
+CF)
1
2
= ×3× (2+3)
1
2
= 7.5
·(BE
B
D
E
C
A
F
4
2
2
O
x
y
-2
y = x+1
1
2
y = x2-4x+8
1
2
B
C
7
A
D
E
F
过点A作AD⊥x轴交直线BC于D,
则AD=3,
过点B作BE⊥AD于E,
则BE=2,
过点C作CF⊥AD交AD的延长线于F,
则CF=3.
S△ABC=
S△ABD
+S△ACD
=
AD ·BE
+ AD ·CF
1
2
1
2
=
AD
+CF)
1
2
= ×3× (2+3)
1
2
= 7.5
·(BE
-2
B
C
7
1
4
2
1
O
x
y
y = x+1
1
2
y = x2-4x+8
1
2
A
求二次函数图象中的三角形面积时,若不能
直接使用三角形面积公式,则经常要用到割补的
方法求解
方法总结
-2
B
C
7
1
4
2
1
O
x
y
y = x+1
1
2
y = x2-4x+8
1
2
A
D
E
S△ABC
-S△ABD
-S△ACE
=S梯形BDEC
1.构造梯形法
求三角形面积的两种常用方法
(补形的方法)
-2
4
2
4
2
O
x
y
y = x+1
1
2
y = x2-4x+8
1
2
B
C
7
A
D
E
F
S△ABC=
S△ABD
+S△ACD
2.铅锤法
求三角形面积的两种常用方法
(割形的方法)
2
6
4
2
O
x
y
-2
B
C
8
A
D
E
S△ABC
-S△ABD
-S△ACE
=S梯形BDEC
2
6
4
2
O
x
y
B
C
D
E
F
S△ABC
S△ABD
+S△ACD
=
1.构造梯形法
2.铅锤法
求三角形面积的两种常用方法
(补)
(割)
(1)本节课学了哪些主要内容?
(2)求三角形面积有什么常用的方法?
课堂小结
巩固提高
1.抛物线y=x2-4与x轴的两个交点和顶点构成
的三角形面积为( ).
A.2 B.4 C.8 D.16
C
2.二次函数y=x2-4x+3的图象与x轴交于点A,
B,与y轴交于点C, 则△ABC面积为( ).
A.1 B.3 C.4 D.6
D
3.直线y=2x+3与抛物线y=x 交于A,B两点,求△OAB的面积.
-2
4
2
3
O
x
y
A
B
C
解:
设直线与y轴交于点C.
解方程组
x1=-1
y1=1,
x2=3
y2=9.
得
∴点A(-1 ,1 ),
则点C(0 ,3 ),
y=2x+3
y=x
点B(3 ,9 ).
OC=3.
∴S△OAB=
S△OCA
+S△OCB
=
OC ·
+ OC ·xB
1
2
1
2
=
×3×1
+ ×3 ×3
1
2
1
2
=6.
| xA |
4.已知抛物线y=x2+bx+c的图象过点A(1,0),
点B,和点C(0, -4).
(1)求抛物线的解析式;
(2)求△ABC面积.
C
A
B
O
x
y
解:
把点A(1,0),点C(0, -4)代入
(1)
y=x2+bx+c,得
1+b+c=0
c=-4
∴
b=3
c=-4
∴所求的抛物线的解析式为
y=x2+3x-4.
4.已知抛物线y=x2+bx+c的图象过点A(1,0),
点B,和点C(0, -4).
(1)求抛物线的解析式;
(2)求△ABC面积.
C
A
B
O
x
y
解:
∵点A(1,0),
(2)
当y=0时,得 x2+3x-4=0.
∴(x-1) (x+4)=0.
∴ x1=1
x2=-4
∴AB=5.
∴点B(-4, 0).
∵点C(0, -4),
∴OC=4.
∴ S△ABC=
AB ·OC
1
2
=
×5×4
1
2
=10.
今天作业
课本P27页第9题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 九年级上册
21.2二次函数的图象和性质(10)
本节课主要是通过例5的学习,学习求抛物线三角形面积(三角形的顶点都在抛物线上)的方法.体会解决问题的转化思想方法.
课件说明
二次函数y=ax2+bx+c图象与系数a,b,c之间的关系
(1)a的符号
抛物线的开口向上
a>0
抛物线的开口向下
a<0
对称轴在y轴左侧
ab>0
对称轴在y轴右侧
ab<0
对称轴是y轴
b=0
抛物线与y轴交于正半轴
c>0
c<0
抛物线经过坐标原点
c=0
抛物线与y轴交于负半轴
(3)c的符号
(2)b的符号
复习旧知
1.抛物线y=ax2+bx+c(a≠0)如图所示,
试确定a、b、c的符号.
x
y
O
a 0, b 0,c 0.
<
<
>
∴a <0
∵抛物线的开口向下
∴c>0
∵抛物线与y轴交于正半轴
∵对称轴在y轴左侧
∴b<0
∴a、b同号
2.抛物线y=ax2+bx+c(a≠0)如图所示,试
判断下来字母和代数式的符号.
a 0, b 0, c 0.
4a+2b+c 0,
4a-2b+c 0.
<
>
>
>
<
x
y
O
1
2
-1
-2
3
例5 抛物线 与直线 交于B,C两点.
y = x2-4x+8
1
2
y = x+1
1
2
(1)在同一平面直角坐标系中画出直线与抛物线;
(2)记抛物线的顶点为A,求△ABC的面积.
学习新知
例5 抛物线 与直线 交于B,C两点.
y = x2-4x+8
1
2
y = x+1
1
2
(1)画出直线 与抛物线 .
解:列表
y = x+1
1
2
y = x2-4x+8
1
2
-2
y
x
0
1
0
-2
y = x+1
1
2
y = x2-4x+8
1
2
B
C
2
6
4
8
2
O
x
y
8
y
x
0
8
2
2
4
0
6
2
2
6
4
8
2
O
x
y
-2
y = x+1
1
2
y = x2-4x+8
1
2
B
C
(2)记抛物线的顶点为A,求△ABC的面积.
8
y = x2-4x+8
1
2
= (x-4)2
1
2
配方得:
∴顶点A的坐标为(4 ,0 ) .
A
求△ABC的面积.
要求得点B、点C的坐标
如何求点B、点C的坐标?
2
6
4
8
2
O
x
y
-2
y = x+1
1
2
y = x2-4x+8
1
2
B
C
8
y = x2-4x+8
1
2
解方程组
A
y = x+1
1
2
如何求点B、点C的坐标?
则需建立直线与抛物线解析式所组成的方程组
y = x2-4x+8
1
2
y = x+1
1
2
解方程组
= x+1
1
2
x2-4x+8
1
2
x2-8x+16=
x+2
x2-9x+14=0
(x-2)(x-7)=0
∴x1=2,
x2=7
y1=2,
y2=4.5
①
②
分别代入①,得
x1=2,
y1=2
x2=7,
y2=4.5.
∴点B的坐标为(2,2)、点C坐标为(7,4.5).
-2
B
C
7
1
4
2
1
O
x
y
y = x+1
1
2
y = x2-4x+8
1
2
A
过点B作BD⊥x轴于D,
过点C作CE⊥x轴于E,
则BD=2,
则CE=4.5,
∴S△ABC
-S△ABD
-S△ACE
=S梯形BDEC
= (BD+CE) ·DE
- AD ·BD
- AE ·CE
1
2
1
2
1
2
DE=5.
D
E
过点B作BD⊥x轴于D,
过点C作CE⊥x轴于E,
则BD=2,
则CE=4.5,
S△ABC
-S△ABD
-S△ACE
=S梯形BDEC
= (BD+CE) ·DE
- AD ·BD
- AE ·CE
1
2
1
2
1
2
= ×(2+4.5)×5
1
2
- ×2×2
- ×3×4.5
1
2
1
2
DE=5.
= 7.5
B
D
E
C
A
-2
B
C
7
1
4
2
1
O
x
y
y = x+1
1
2
y = x2-4x+8
1
2
A
过点B作BD⊥x轴于D,
过点C作CE⊥x轴于E,
则BD=2,
则CE=4.5,
S△ABC
-S△ABD
-S△ACE
=S梯形BDEC
= (BD+CE) ·DE
- AD ·BD
- AE ·CE
1
2
1
2
1
2
= ×(2+4.5)×5
1
2
- ×2×2
- ×3×4.5
1
2
1
2
DE=5.
= 7.5
D
E
2
6
4
2
O
x
y
-2
B
C
8
y = x2-4x+8
1
2
解方程组
A
y = x+1
1
2
x1=2
y1=2,
x2=7
y2=4.5.
得
∴点B的坐标为(2 ,2 ),
点C的坐标为(7 ,4.5 ).
D
E
过点B作BD⊥x轴于D,
过点C作CE⊥x轴于E,
则BD=2,
则CE=4.5.
DE=5.
S△ABC
-S△ABD
-S△ACE
=S梯形BDEC
= (BD+CE) ·DE
- AD ·BD
- AE ·CE
1
2
1
2
1
2
= ×(2+4.5)×5
1
2
- ×2×2
- ×3×4.5
1
2
1
2
= 7.5
4
2
2
O
x
y
-2
y = x+1
1
2
y = x2-4x+8
1
2
B
C
7
A
D
过点A作AD⊥x轴交直线BC于D,
则AD=3,
(4 , 3) .
解法2
铅垂法
过函数图象上的点作坐标轴的垂线的方法
则点D的横坐标为4,
∵点D在直线BC上,
∴点D的纵坐标为3.
4
2
2
O
x
y
-2
y = x+1
1
2
y = x2-4x+8
1
2
B
C
7
A
D
E
F
过点A作AD⊥x轴交直线BC于D,
则AD=3,
过点B作BE⊥AD于E,
则BE=2,
过点C作CF⊥AD交AD的延长线于F,
则CF=3.
S△ABC=
S△ABD
+S△ACD
=
AD ·BE
+ AD ·CF
1
2
1
2
(4 , 3) .
过点A作AD⊥x轴交直线BC于D,
则AD=3,
过点B作BE⊥AD于E,
则BE=2,
过点C作CF⊥AD交AD的延长线于F,
则CF=3.
S△ABC=
S△ABD
+S△ACD
=
AD ·BE
+ AD ·CF
1
2
1
2
=
AD
+CF)
1
2
= ×3× (2+3)
1
2
= 7.5
·(BE
B
D
E
C
A
F
4
2
2
O
x
y
-2
y = x+1
1
2
y = x2-4x+8
1
2
B
C
7
A
D
E
F
过点A作AD⊥x轴交直线BC于D,
则AD=3,
过点B作BE⊥AD于E,
则BE=2,
过点C作CF⊥AD交AD的延长线于F,
则CF=3.
S△ABC=
S△ABD
+S△ACD
=
AD ·BE
+ AD ·CF
1
2
1
2
=
AD
+CF)
1
2
= ×3× (2+3)
1
2
= 7.5
·(BE
-2
B
C
7
1
4
2
1
O
x
y
y = x+1
1
2
y = x2-4x+8
1
2
A
求二次函数图象中的三角形面积时,若不能
直接使用三角形面积公式,则经常要用到割补的
方法求解
方法总结
-2
B
C
7
1
4
2
1
O
x
y
y = x+1
1
2
y = x2-4x+8
1
2
A
D
E
S△ABC
-S△ABD
-S△ACE
=S梯形BDEC
1.构造梯形法
求三角形面积的两种常用方法
(补形的方法)
-2
4
2
4
2
O
x
y
y = x+1
1
2
y = x2-4x+8
1
2
B
C
7
A
D
E
F
S△ABC=
S△ABD
+S△ACD
2.铅锤法
求三角形面积的两种常用方法
(割形的方法)
2
6
4
2
O
x
y
-2
B
C
8
A
D
E
S△ABC
-S△ABD
-S△ACE
=S梯形BDEC
2
6
4
2
O
x
y
B
C
D
E
F
S△ABC
S△ABD
+S△ACD
=
1.构造梯形法
2.铅锤法
求三角形面积的两种常用方法
(补)
(割)
(1)本节课学了哪些主要内容?
(2)求三角形面积有什么常用的方法?
课堂小结
巩固提高
1.抛物线y=x2-4与x轴的两个交点和顶点构成
的三角形面积为( ).
A.2 B.4 C.8 D.16
C
2.二次函数y=x2-4x+3的图象与x轴交于点A,
B,与y轴交于点C, 则△ABC面积为( ).
A.1 B.3 C.4 D.6
D
3.直线y=2x+3与抛物线y=x 交于A,B两点,求△OAB的面积.
-2
4
2
3
O
x
y
A
B
C
解:
设直线与y轴交于点C.
解方程组
x1=-1
y1=1,
x2=3
y2=9.
得
∴点A(-1 ,1 ),
则点C(0 ,3 ),
y=2x+3
y=x
点B(3 ,9 ).
OC=3.
∴S△OAB=
S△OCA
+S△OCB
=
OC ·
+ OC ·xB
1
2
1
2
=
×3×1
+ ×3 ×3
1
2
1
2
=6.
| xA |
4.已知抛物线y=x2+bx+c的图象过点A(1,0),
点B,和点C(0, -4).
(1)求抛物线的解析式;
(2)求△ABC面积.
C
A
B
O
x
y
解:
把点A(1,0),点C(0, -4)代入
(1)
y=x2+bx+c,得
1+b+c=0
c=-4
∴
b=3
c=-4
∴所求的抛物线的解析式为
y=x2+3x-4.
4.已知抛物线y=x2+bx+c的图象过点A(1,0),
点B,和点C(0, -4).
(1)求抛物线的解析式;
(2)求△ABC面积.
C
A
B
O
x
y
解:
∵点A(1,0),
(2)
当y=0时,得 x2+3x-4=0.
∴(x-1) (x+4)=0.
∴ x1=1
x2=-4
∴AB=5.
∴点B(-4, 0).
∵点C(0, -4),
∴OC=4.
∴ S△ABC=
AB ·OC
1
2
=
×5×4
1
2
=10.
今天作业
课本P27页第9题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
