北师大版八年级上册1.2一定是直角三角形吗?课件(共14张PPT)
文档属性
| 名称 | 北师大版八年级上册1.2一定是直角三角形吗?课件(共14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 245.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-26 08:32:50 | ||
图片预览






文档简介
(共14张PPT)
第一章 勾股定理
1.2 一定是直角三角形吗
北师大版八年级上册
1
学习目标
1、探索勾股定理的逆定理;
2、掌握勾股定理的逆定理,并能进行简单应用。
1、已知在Rt△ABC中,∠C=90°,若AB=25,BC=15,则AC=________.
2、已知三角形的三边长分别为3cm、4cm、5cm,求作:△ABC,使AC=3cm, BC=4cm,AB=5cm。(用尺规作图)
学习准备
自学指导1
根据下列要求阅读并完成书第9页“做一做”的内容,时间3分钟.
(1)借助于量角器或直角三角板判断所得的三角形是直角三角形吗?
(2)如果三角形的三边长a,b,c满足_________,那么这个三角形是直角三角形。
(3)满足_______________的三个 ,称为 。
正整数
勾股数
常见的勾股数有:
3,4,5; 5,12,13;
7,24,25; 8,15,17 .
一组勾股数,都扩大相同倍数k(k为正整数),得到一组新数,这组数同样是勾股数.
知识归纳
如果三角形的三边长a,b,c满足a2+b2=c2 ,那么这个三角形是直角三角形.
符号语言:
如图,∵在△ABC中,a2+b2=c2 ,
∴ △ABC是直角三角形,∠C=90°.
满足a2+b2=c2的三个正整数,称为勾股数.
下列几组数能否作为直角三角形的三边长 说说你的理由.
(1)6,8,10 (2)7,24,25
(3)12, 18, 22 (4)0.3,0.4,0.5
(5)9,12,15 (6)8,15,17
(7)5,12,13 (8)3,6,7
自学检测1
哪些是勾股数?
学习例题
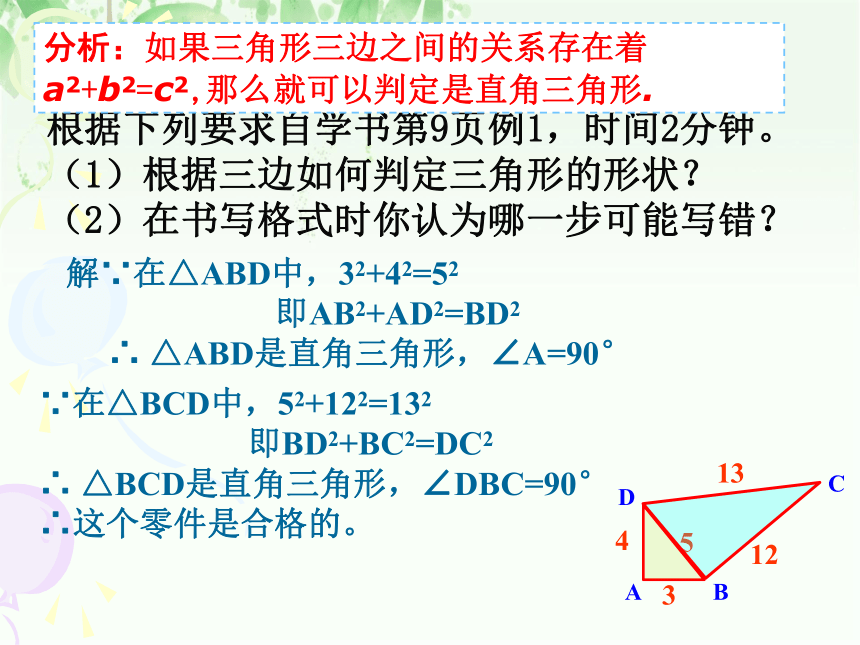
根据下列要求自学书第9页例1,时间2分钟。
(1)根据三边如何判定三角形的形状?
(2)在书写格式时你认为哪一步可能写错?
3
4
13
12
5
A
B
C
D
解∵在△ABD中,32+42=52
即AB2+AD2=BD2
∴ △ABD是直角三角形,∠A=90°
∵在△BCD中,52+122=132
即BD2+BC2=DC2
∴ △BCD是直角三角形,∠DBC=90°
∴这个零件是合格的。
分析:如果三角形三边之间的关系存在着a2+b2=c2,那么就可以判定是直角三角形.
1、已知四边形ABCD中,AB=3cm,AD=4cm,CD=12cm,
BC=13cm,且∠DAB=90°。
试判断△BCD的形状。
自学检测2
2.一个三角形的三边的长分别是15cm,20cm,
25cm,则这个三角形的面积是______cm2.
3.如图,在正方形ABCD中,AB=4,AE=2,DF=1,图中有几个直角三角形,你是如何判断的?
4
1
2
2
4
3
解:△ABE,△DEF,△FCB
均为直角三角形,
由勾股定理知
BE2=22+42=20,EF2=22+12=5,
BF2=32+42=25,
所以BE2+EF2=BF2,
所以△BEF是直角三角形.
4.如图,哪些是直角三角形,哪些不是,说说你的理由?
①
②
③
④
⑤
⑥
答案:
④⑤是直角三角形
①②③⑥不是直角三角形
课本P11 随堂练习 第4题
5.如果三条线段a,b,c满足a2=c2-b2, 这三条线段组成的三角形是直角三角形吗 为什么
变式:若一个三角形的三边a、b、c满足等式(a+b)2-2ab=c2,则此三角形的形状
为_____________。
勾股定理
的逆定理
内容
作用
从三边数量关系判定一个三角形是否是直角形三角形.
如果三角形的三边长a 、b 、c满足a2+b2=c2,那么这个三角形是直角三角形.
注意
最长边不一定是c, ∠C也不一定是直角.
勾股数一定是正整数
勾股数
归纳新知
2.已知(x-12)2+|y-5|+(z-13)2=0,判断以x,y,z为边的三角形是什么三角形.
作业:
1.已知直角三角形的两边长分别为3和4,
若第三边的长为c,则c2=___.
3. 如图,每个小正方形的边长为1,点A,B,C是小正方形的顶点,
则∠ABC=________.
4. 如图是一块地,已知AD=8 m,CD=6 m,∠D=90°,AB=26 m,BC=24 m,求这块地的面积,若每平方米草皮需要投入200元,问一共要投入多少元?
14
第一章 勾股定理
1.2 一定是直角三角形吗
北师大版八年级上册
1
学习目标
1、探索勾股定理的逆定理;
2、掌握勾股定理的逆定理,并能进行简单应用。
1、已知在Rt△ABC中,∠C=90°,若AB=25,BC=15,则AC=________.
2、已知三角形的三边长分别为3cm、4cm、5cm,求作:△ABC,使AC=3cm, BC=4cm,AB=5cm。(用尺规作图)
学习准备
自学指导1
根据下列要求阅读并完成书第9页“做一做”的内容,时间3分钟.
(1)借助于量角器或直角三角板判断所得的三角形是直角三角形吗?
(2)如果三角形的三边长a,b,c满足_________,那么这个三角形是直角三角形。
(3)满足_______________的三个 ,称为 。
正整数
勾股数
常见的勾股数有:
3,4,5; 5,12,13;
7,24,25; 8,15,17 .
一组勾股数,都扩大相同倍数k(k为正整数),得到一组新数,这组数同样是勾股数.
知识归纳
如果三角形的三边长a,b,c满足a2+b2=c2 ,那么这个三角形是直角三角形.
符号语言:
如图,∵在△ABC中,a2+b2=c2 ,
∴ △ABC是直角三角形,∠C=90°.
满足a2+b2=c2的三个正整数,称为勾股数.
下列几组数能否作为直角三角形的三边长 说说你的理由.
(1)6,8,10 (2)7,24,25
(3)12, 18, 22 (4)0.3,0.4,0.5
(5)9,12,15 (6)8,15,17
(7)5,12,13 (8)3,6,7
自学检测1
哪些是勾股数?
学习例题
根据下列要求自学书第9页例1,时间2分钟。
(1)根据三边如何判定三角形的形状?
(2)在书写格式时你认为哪一步可能写错?
3
4
13
12
5
A
B
C
D
解∵在△ABD中,32+42=52
即AB2+AD2=BD2
∴ △ABD是直角三角形,∠A=90°
∵在△BCD中,52+122=132
即BD2+BC2=DC2
∴ △BCD是直角三角形,∠DBC=90°
∴这个零件是合格的。
分析:如果三角形三边之间的关系存在着a2+b2=c2,那么就可以判定是直角三角形.
1、已知四边形ABCD中,AB=3cm,AD=4cm,CD=12cm,
BC=13cm,且∠DAB=90°。
试判断△BCD的形状。
自学检测2
2.一个三角形的三边的长分别是15cm,20cm,
25cm,则这个三角形的面积是______cm2.
3.如图,在正方形ABCD中,AB=4,AE=2,DF=1,图中有几个直角三角形,你是如何判断的?
4
1
2
2
4
3
解:△ABE,△DEF,△FCB
均为直角三角形,
由勾股定理知
BE2=22+42=20,EF2=22+12=5,
BF2=32+42=25,
所以BE2+EF2=BF2,
所以△BEF是直角三角形.
4.如图,哪些是直角三角形,哪些不是,说说你的理由?
①
②
③
④
⑤
⑥
答案:
④⑤是直角三角形
①②③⑥不是直角三角形
课本P11 随堂练习 第4题
5.如果三条线段a,b,c满足a2=c2-b2, 这三条线段组成的三角形是直角三角形吗 为什么
变式:若一个三角形的三边a、b、c满足等式(a+b)2-2ab=c2,则此三角形的形状
为_____________。
勾股定理
的逆定理
内容
作用
从三边数量关系判定一个三角形是否是直角形三角形.
如果三角形的三边长a 、b 、c满足a2+b2=c2,那么这个三角形是直角三角形.
注意
最长边不一定是c, ∠C也不一定是直角.
勾股数一定是正整数
勾股数
归纳新知
2.已知(x-12)2+|y-5|+(z-13)2=0,判断以x,y,z为边的三角形是什么三角形.
作业:
1.已知直角三角形的两边长分别为3和4,
若第三边的长为c,则c2=___.
3. 如图,每个小正方形的边长为1,点A,B,C是小正方形的顶点,
则∠ABC=________.
4. 如图是一块地,已知AD=8 m,CD=6 m,∠D=90°,AB=26 m,BC=24 m,求这块地的面积,若每平方米草皮需要投入200元,问一共要投入多少元?
14
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
