人教版九年级上册21.3 实际问题与一元二次方程 课件 (共17张PPT)
文档属性
| 名称 | 人教版九年级上册21.3 实际问题与一元二次方程 课件 (共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-27 07:25:17 | ||
图片预览





文档简介
(共17张PPT)
21.3 实际问题与一元二次方程
增长率问题
九年级数学上册
目录CONTENTS复习回顾:
1.解一元二次方程有哪些方法?
直接开平方法、配方法、公式法、因式分解法.
2.列方程解应用题的一般步骤?
①审题 ②设未知数 ③找等量关系 ④列方程 ⑤解方程
⑥答
导入
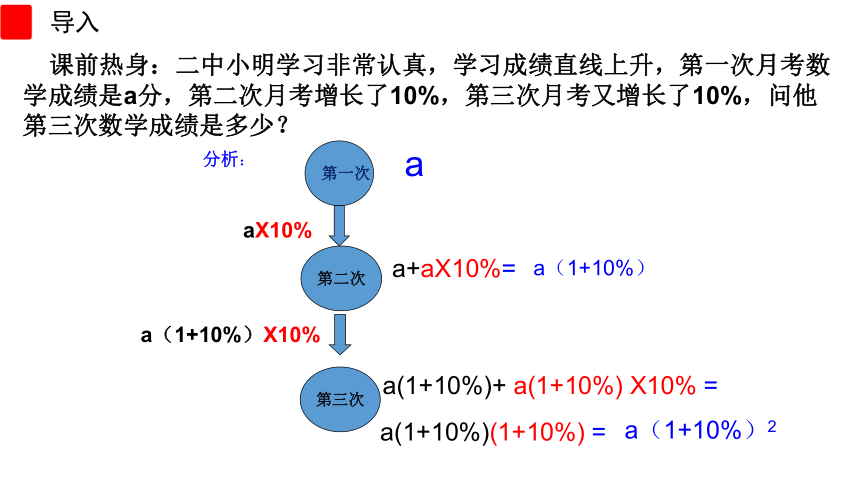
课前热身:二中小明学习非常认真,学习成绩直线上升,第一次月考数学成绩是a分,第二次月考增长了10%,第三次月考又增长了10%,问他第三次数学成绩是多少?
分析:
第三次
第二次
第一次
a
aX10%
a+aX10%=
a(1+10%)X10%
a(1+10%)+ a(1+10%) X10% =
a(1+10%)2
a(1+10%)
导入
a(1+10%)(1+10%) =
平均增长(降低)率问题:
1.增长率问题:设基数为a,平均增长率为x,则一次增长后的值为_
__ ,二次增长后的值为_ ___.
2.降低率问题:若基数为a,平均降低率为x,则一次降低后的值为_
______,二次降低后的值为_______.
a(1+x)
a(1-x)
知识讲解
规律总结:
类似地 这种增长率的问题在实际生活普遍存在,有一定的模式
若变化前后的量分别为a,b ,变化的增长率(降低率)为x,增长或降低的的次数为2,则它们的数量关系可表示为
知识讲解
用直接开平方法解这类方程比较简单
(其中增长取+,降低取-)
更一般的增长或降低的的次数为n,则它们的数量关系可表示为
知识拓展
例:某工厂一月份的产值是5万元, 三月份的产值是11.25万元, 求月平均增长率是多少
知识讲解
某种药剂原售价为4元, 经过两次降价, 现在每瓶售价为2.56元,问平均每次降价百分率
课堂练习
解:设平均每次降价百分率为x,根据题意,得
答:平均每次降价百分率为20%
小 结
1、平均增长(降低)率公式
2、注意:
(1)1与x的位置不要调换
(2)注意检验方程的解是否符合题意
(3)解这类问题列出的方程一般用 直接开平方法
实际问题与一元二次方程
------销售利润问题
通过列方程解应用题,进一步提高逻辑思维能力和分析问题、解决问题的能力.
学会列一元二次方程解决有关销售利润问题.
※商品总利润=单件利润×销售数量
常见的几个量有:进价,售价,利润,利润率.
我们学过的有关销售利润问题中常见的量有哪些?它们之间有怎样的数量关系?
数量关系:
例1:某超市将进货单价为40元的商品按50元出售时,能卖500个,已知该商品要涨价1元,其销售量就要减少10个,为了赚8000元利润,售价应定为多少,这时应进货为多少个?
【分析】设商品单价为(50+x)元,则每个商品得利润[(50+x)-40]元,因为每涨价1元,其销售会减少10,则每个涨价x元,其销售量会减少10x个,故销售量为(500-10x)个,根据每件商品的利润×件数=8000,则可列方程为:
(500-10x) [(50+x)-40]=8000
典例解析
解:设每个商品涨价x元,则销售价为(50+x)元,销售量为(500-10x)个,则
(500-10x) [(50+x)-40]=8000,
整理得 x2-40x+300=0,
解得x1=10,x2=30都符合题意.
当x=10时,50+x =60,500-10 x=400;
当x=30时,50+x =80, 500-10 x=200.
答:要想赚8000元,售价为60元或80元;若售价为60元,则进货量应为400;若售价为80元,则进货量应为200个.
典例解析
例2. 某商店从厂家以每件21元的价格购进一批商品,若每件商品售价为x元,则每天可卖出(350-10x)件,但物价局限定每件商品加价不能超过进价的20%.商店要想每天赚400元,需要卖出多少件商品 每件商品的售价应为多少元
典例解析
小结梳理
二、解题过程分析策略:
一、销售利润问题等量关系:
1.仔细审读找出贯穿全题的等量关系;
2.分析题中相关数量相之间关系,适当设未知数,并用含未知数的代数式表示相关的量,从而列出方程;
3.整理方程并解出方程;
4.结合题中实际意义,对方程的根取舍;
5.总结作答.
※单件利润=售价—进价
※商品总利润=单件利润×销售数量
谢谢聆听
21.3 实际问题与一元二次方程
增长率问题
九年级数学上册
目录CONTENTS复习回顾:
1.解一元二次方程有哪些方法?
直接开平方法、配方法、公式法、因式分解法.
2.列方程解应用题的一般步骤?
①审题 ②设未知数 ③找等量关系 ④列方程 ⑤解方程
⑥答
导入
课前热身:二中小明学习非常认真,学习成绩直线上升,第一次月考数学成绩是a分,第二次月考增长了10%,第三次月考又增长了10%,问他第三次数学成绩是多少?
分析:
第三次
第二次
第一次
a
aX10%
a+aX10%=
a(1+10%)X10%
a(1+10%)+ a(1+10%) X10% =
a(1+10%)2
a(1+10%)
导入
a(1+10%)(1+10%) =
平均增长(降低)率问题:
1.增长率问题:设基数为a,平均增长率为x,则一次增长后的值为_
__ ,二次增长后的值为_ ___.
2.降低率问题:若基数为a,平均降低率为x,则一次降低后的值为_
______,二次降低后的值为_______.
a(1+x)
a(1-x)
知识讲解
规律总结:
类似地 这种增长率的问题在实际生活普遍存在,有一定的模式
若变化前后的量分别为a,b ,变化的增长率(降低率)为x,增长或降低的的次数为2,则它们的数量关系可表示为
知识讲解
用直接开平方法解这类方程比较简单
(其中增长取+,降低取-)
更一般的增长或降低的的次数为n,则它们的数量关系可表示为
知识拓展
例:某工厂一月份的产值是5万元, 三月份的产值是11.25万元, 求月平均增长率是多少
知识讲解
某种药剂原售价为4元, 经过两次降价, 现在每瓶售价为2.56元,问平均每次降价百分率
课堂练习
解:设平均每次降价百分率为x,根据题意,得
答:平均每次降价百分率为20%
小 结
1、平均增长(降低)率公式
2、注意:
(1)1与x的位置不要调换
(2)注意检验方程的解是否符合题意
(3)解这类问题列出的方程一般用 直接开平方法
实际问题与一元二次方程
------销售利润问题
通过列方程解应用题,进一步提高逻辑思维能力和分析问题、解决问题的能力.
学会列一元二次方程解决有关销售利润问题.
※商品总利润=单件利润×销售数量
常见的几个量有:进价,售价,利润,利润率.
我们学过的有关销售利润问题中常见的量有哪些?它们之间有怎样的数量关系?
数量关系:
例1:某超市将进货单价为40元的商品按50元出售时,能卖500个,已知该商品要涨价1元,其销售量就要减少10个,为了赚8000元利润,售价应定为多少,这时应进货为多少个?
【分析】设商品单价为(50+x)元,则每个商品得利润[(50+x)-40]元,因为每涨价1元,其销售会减少10,则每个涨价x元,其销售量会减少10x个,故销售量为(500-10x)个,根据每件商品的利润×件数=8000,则可列方程为:
(500-10x) [(50+x)-40]=8000
典例解析
解:设每个商品涨价x元,则销售价为(50+x)元,销售量为(500-10x)个,则
(500-10x) [(50+x)-40]=8000,
整理得 x2-40x+300=0,
解得x1=10,x2=30都符合题意.
当x=10时,50+x =60,500-10 x=400;
当x=30时,50+x =80, 500-10 x=200.
答:要想赚8000元,售价为60元或80元;若售价为60元,则进货量应为400;若售价为80元,则进货量应为200个.
典例解析
例2. 某商店从厂家以每件21元的价格购进一批商品,若每件商品售价为x元,则每天可卖出(350-10x)件,但物价局限定每件商品加价不能超过进价的20%.商店要想每天赚400元,需要卖出多少件商品 每件商品的售价应为多少元
典例解析
小结梳理
二、解题过程分析策略:
一、销售利润问题等量关系:
1.仔细审读找出贯穿全题的等量关系;
2.分析题中相关数量相之间关系,适当设未知数,并用含未知数的代数式表示相关的量,从而列出方程;
3.整理方程并解出方程;
4.结合题中实际意义,对方程的根取舍;
5.总结作答.
※单件利润=售价—进价
※商品总利润=单件利润×销售数量
谢谢聆听
同课章节目录
