13.3.2 等边三角形(2)课件
文档属性
| 名称 | 13.3.2 等边三角形(2)课件 |  | |
| 格式 | zip | ||
| 文件大小 | 189.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-09-21 22:40:54 | ||
图片预览




文档简介
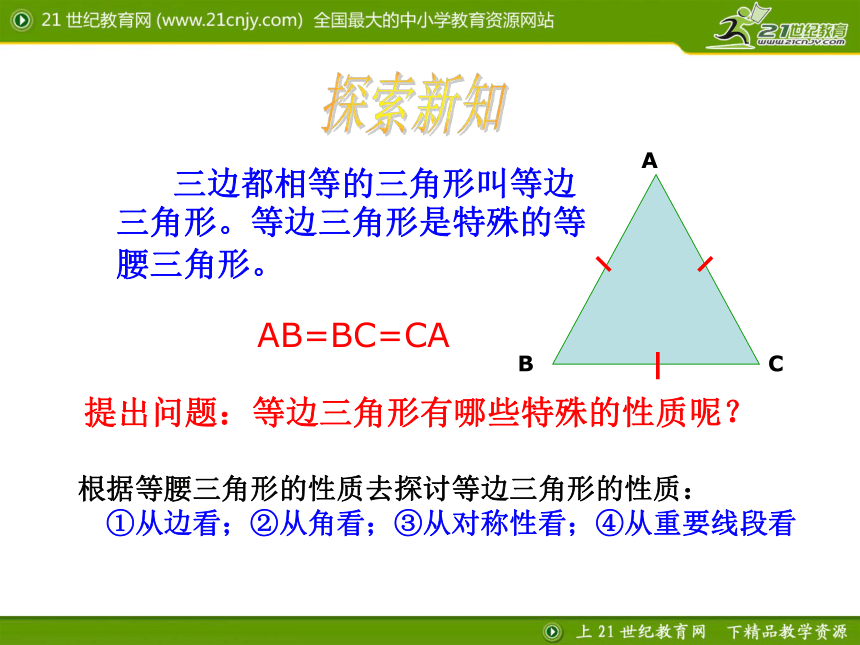
课件16张PPT。13.3.2 等边三角形(2) 三边都相等的三角形叫等边三角形。等边三角形是特殊的等腰三角形。 探索新知AB=BC=CA提出问题:等边三角形有哪些特殊的性质呢? 根据等腰三角形的性质去探讨等边三角形的性质:
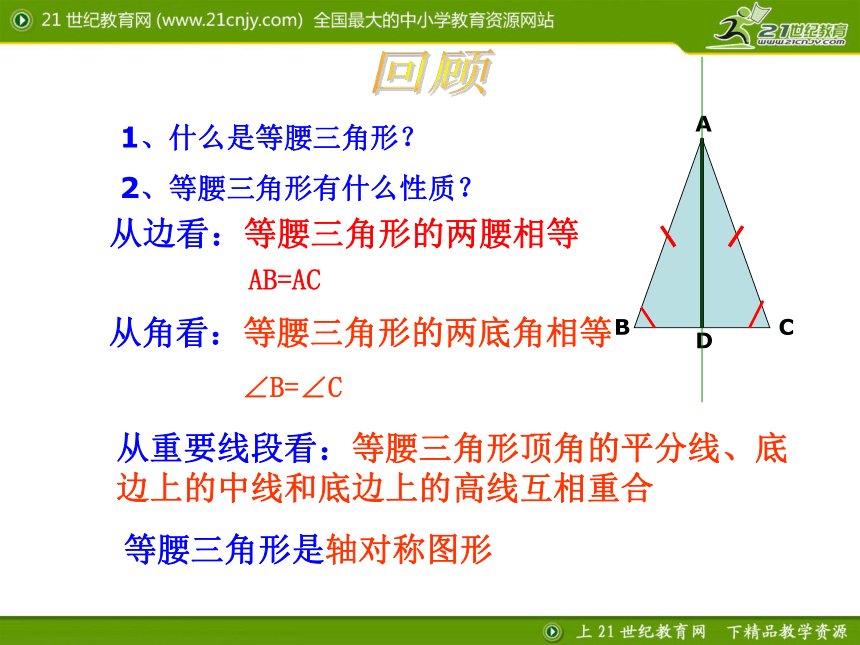
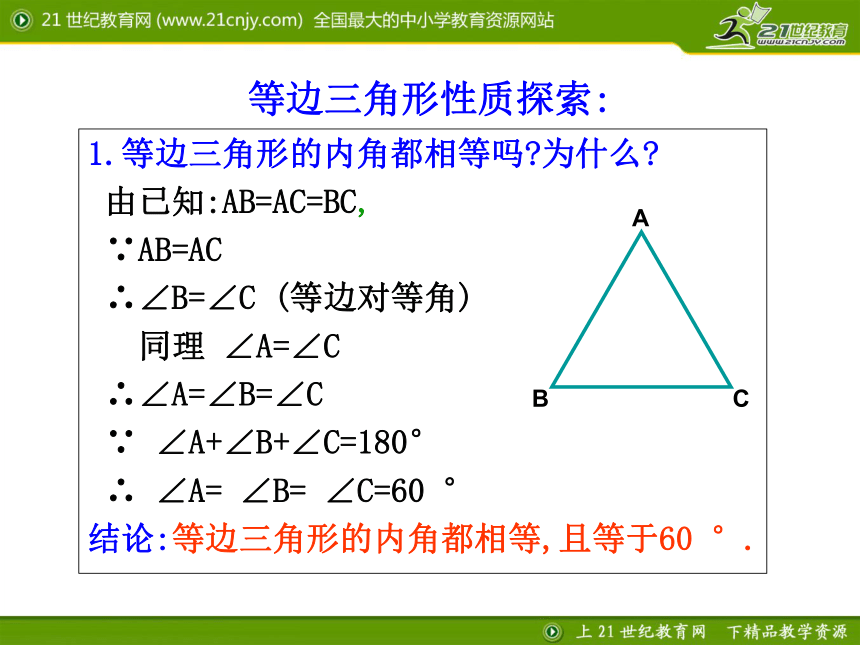
①从边看;②从角看;③从对称性看;④从重要线段看1、什么是等腰三角形?2、等腰三角形有什么性质?从边看:等腰三角形的两腰相等 从角看:等腰三角形的两底角相等 从重要线段看:等腰三角形顶角的平分线、底边上的中线和底边上的高线互相重合 回顾AB=AC∠B=∠CD等腰三角形是轴对称图形 1.等边三角形的内角都相等吗?为什么?
由已知:AB=AC=BC,
∵AB=AC
∴∠B=∠C (等边对等角)
同理 ∠A=∠C
∴∠A=∠B=∠C
∵ ∠A+∠B+∠C=180°
∴ ∠A= ∠B= ∠C=60 °
结论:等边三角形的内角都相等,且等于60 °.等边三角形性质探索:ABC2.等边三角形是轴对称图形吗?
若是,有几条对称轴?
结论:等边三角形是轴对称图形,
有三条对称轴.等边三角形性质探索:3.等边三角形每边上的中线,高和所对角的平分线都三线合一吗?为什么?
结论:等边三角形各边上中线,高和所对角的平分线都三线合一,它们交于一点,这点叫三角形的中心.ABCO等边三角形性质探索:1、等边三角形的三个内角都相等,且等于60°;
2、三个内角都等于60°的三角形一定是等边三角形。
三个角都相等的三角形是等边三角形。
有一个角是60°的等腰三角形是等边三角形。
3、等边三角形是轴对称图形,等边三角形每一条边上的中线、高和所对角的平分线都三线合一,它们所在的直线都是等边三角形的对称轴。等边三角形的性质与判定1.三边都相等的三角形叫做____三角形.
2.等边三角形的每个内角都等于____度.
3.等边三角形有____条对称轴.
4.等边三角形的对称轴的交点叫___.
等边三角形绕中心至少旋转___度.才能和
原来的三角形重合.练习1等边603中心120例1:如图,⊿ABC是等边三角形,DE//BC,交AB,AC于D,E.求证⊿ADE是等边三角形。ABCED证明:∵⊿ABC是等边三角形,
∴∠A=∠B=∠C.
∵DE//BC,
∴∠ADE=∠B, ∠AED =∠C.
∴ ⊿ADE是等边三角形.想一想这道题还有其它证法么?∵△ABC与△ADC关于AC轴对称
∴AB=AD
△ABD是等边三角形
又∵AC⊥BD∴BC=DC=1/2AB如图,将两个含有30°角的三角形放在一起,你能借助这个图形,找到Rt△ABC与斜边AB之间的数量关系吗?探究二在直角三角形中,如果一个锐角等于30°
那么它所对的直角边等于斜边的一半.A在直角△ABC中
∵∠A=30°
∴AC=2BC例2,下图是屋架设计图的一部分,点D是
斜梁AB的中点,立柱BC、DE垂直于横梁AC,
AB=7.4m,∠A=30°立柱BC 、 DE要多长?AB解:∵DE⊥AC, BC⊥AC, ∠A=30°
可得 2BC=AB, 2DE=AD
∴BC=1/2 ×7.4=3.7m
又 AD=1/2 AB
∴DE=1/2 AD=1/2 ×3.7=1.85m
答:立柱BC的长是3.7m,DE的长是
1.85m.1、如图1,△ABC中,AB=AC,∠C=30°,DA⊥BA于A,BC=14.4cm,则AD= 2、如图2, ∠C=90°,D是CA的延长线上一点, ∠BDC=15 °,且AD=AB,则BC AD4.8=(1).等边三角形的性质.
小结:1.等边三角形的内角都相等,且都等于60 °
2.等边三角形是轴对称图形,有三条对称轴.
3.等边三角形各边上中线,高和所对角的平分线都三线合一.(2) 等边三角形的判定:1.三边相等的三角形是等边三角形.
2.三个内角都等于60 °的三角形是等边三角形.
3.有一个内角等于60 °的等腰三角形是等边三角形.
①从边看;②从角看;③从对称性看;④从重要线段看1、什么是等腰三角形?2、等腰三角形有什么性质?从边看:等腰三角形的两腰相等 从角看:等腰三角形的两底角相等 从重要线段看:等腰三角形顶角的平分线、底边上的中线和底边上的高线互相重合 回顾AB=AC∠B=∠CD等腰三角形是轴对称图形 1.等边三角形的内角都相等吗?为什么?
由已知:AB=AC=BC,
∵AB=AC
∴∠B=∠C (等边对等角)
同理 ∠A=∠C
∴∠A=∠B=∠C
∵ ∠A+∠B+∠C=180°
∴ ∠A= ∠B= ∠C=60 °
结论:等边三角形的内角都相等,且等于60 °.等边三角形性质探索:ABC2.等边三角形是轴对称图形吗?
若是,有几条对称轴?
结论:等边三角形是轴对称图形,
有三条对称轴.等边三角形性质探索:3.等边三角形每边上的中线,高和所对角的平分线都三线合一吗?为什么?
结论:等边三角形各边上中线,高和所对角的平分线都三线合一,它们交于一点,这点叫三角形的中心.ABCO等边三角形性质探索:1、等边三角形的三个内角都相等,且等于60°;
2、三个内角都等于60°的三角形一定是等边三角形。
三个角都相等的三角形是等边三角形。
有一个角是60°的等腰三角形是等边三角形。
3、等边三角形是轴对称图形,等边三角形每一条边上的中线、高和所对角的平分线都三线合一,它们所在的直线都是等边三角形的对称轴。等边三角形的性质与判定1.三边都相等的三角形叫做____三角形.
2.等边三角形的每个内角都等于____度.
3.等边三角形有____条对称轴.
4.等边三角形的对称轴的交点叫___.
等边三角形绕中心至少旋转___度.才能和
原来的三角形重合.练习1等边603中心120例1:如图,⊿ABC是等边三角形,DE//BC,交AB,AC于D,E.求证⊿ADE是等边三角形。ABCED证明:∵⊿ABC是等边三角形,
∴∠A=∠B=∠C.
∵DE//BC,
∴∠ADE=∠B, ∠AED =∠C.
∴ ⊿ADE是等边三角形.想一想这道题还有其它证法么?∵△ABC与△ADC关于AC轴对称
∴AB=AD
△ABD是等边三角形
又∵AC⊥BD∴BC=DC=1/2AB如图,将两个含有30°角的三角形放在一起,你能借助这个图形,找到Rt△ABC与斜边AB之间的数量关系吗?探究二在直角三角形中,如果一个锐角等于30°
那么它所对的直角边等于斜边的一半.A在直角△ABC中
∵∠A=30°
∴AC=2BC例2,下图是屋架设计图的一部分,点D是
斜梁AB的中点,立柱BC、DE垂直于横梁AC,
AB=7.4m,∠A=30°立柱BC 、 DE要多长?AB解:∵DE⊥AC, BC⊥AC, ∠A=30°
可得 2BC=AB, 2DE=AD
∴BC=1/2 ×7.4=3.7m
又 AD=1/2 AB
∴DE=1/2 AD=1/2 ×3.7=1.85m
答:立柱BC的长是3.7m,DE的长是
1.85m.1、如图1,△ABC中,AB=AC,∠C=30°,DA⊥BA于A,BC=14.4cm,则AD= 2、如图2, ∠C=90°,D是CA的延长线上一点, ∠BDC=15 °,且AD=AB,则BC AD4.8=(1).等边三角形的性质.
小结:1.等边三角形的内角都相等,且都等于60 °
2.等边三角形是轴对称图形,有三条对称轴.
3.等边三角形各边上中线,高和所对角的平分线都三线合一.(2) 等边三角形的判定:1.三边相等的三角形是等边三角形.
2.三个内角都等于60 °的三角形是等边三角形.
3.有一个内角等于60 °的等腰三角形是等边三角形.
