人教版九年级上册22.1.4 二次函数y=ax2+bx+c的图象和性质 课件 (共20张PPT)
文档属性
| 名称 | 人教版九年级上册22.1.4 二次函数y=ax2+bx+c的图象和性质 课件 (共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 958.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-27 07:53:18 | ||
图片预览

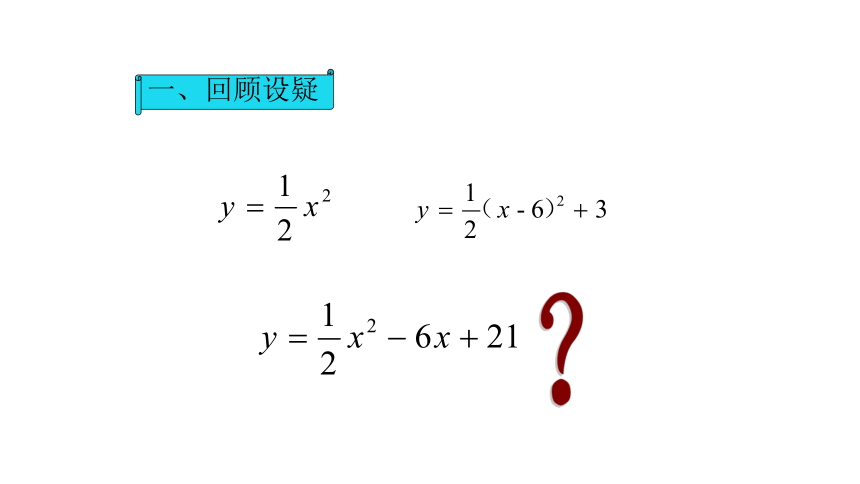




文档简介
(共20张PPT)
人教版九年级上册
22.1.4 二次函数y=ax2+bx+c的图象和性质(1)
一、回顾设疑
?
(x-6)+3
2
=
=(x2-12x)+21
=(x2-12x+36-36)+21
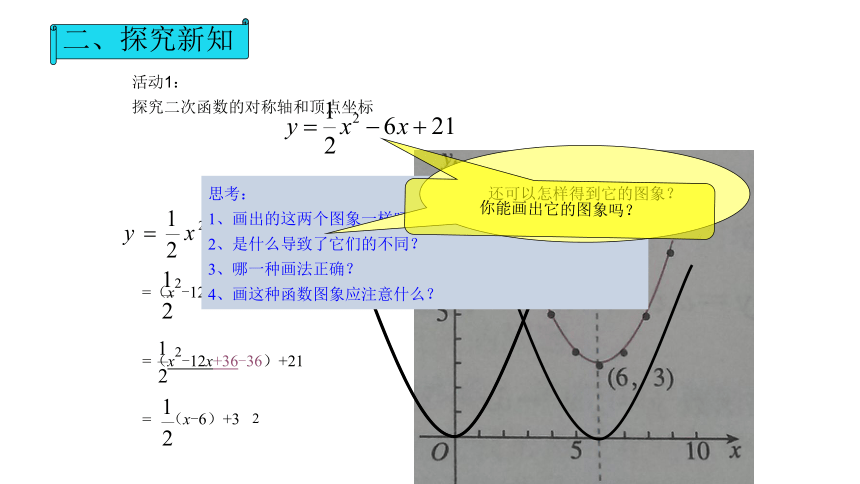
活动1:
探究二次函数的对称轴和顶点坐标
思考:
1、画出的这两个图象一样吗?
2、是什么导致了它们的不同?
3、哪一种画法正确?
4、画这种函数图象应注意什么?
二、探究新知
还可以怎样得到它的图象?
你能画出它的图象吗?
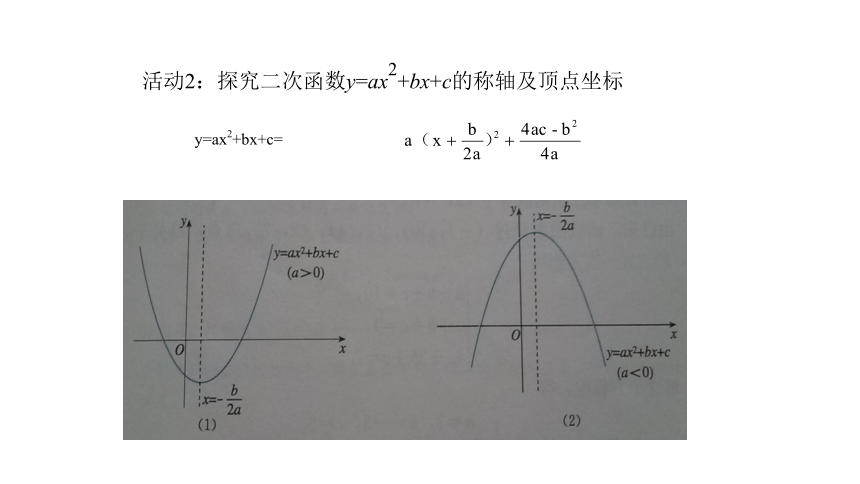
活动2:探究二次函数y=ax2+bx+c的称轴及顶点坐标
y=ax2+bx+c=
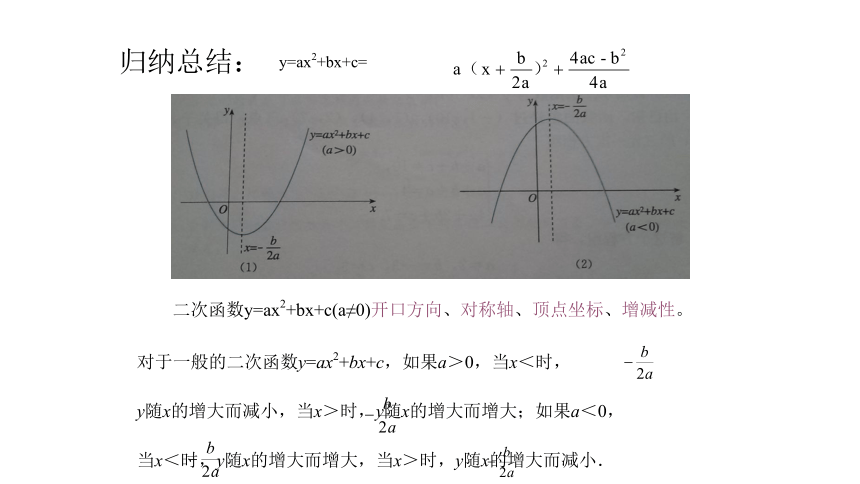
对于一般的二次函数y=ax2+bx+c,如果a>0,当x<时,
y随x的增大而减小,当x>时,y随x的增大而增大;如果a<0,
当x<时,y随x的增大而增大,当x>时,y随x的增大而减小.
归纳总结:
二次函数y=ax2+bx+c(a≠0)开口方向、对称轴、顶点坐标、增减性。
y=ax2+bx+c=
练习:
用公式法求抛物线y=-x2+2x-3的对称轴和顶点坐标。
这节课你都学到了什么?学会了哪些方法?还有什么困惑?
求二次函数y=ax2+bx+c的对称轴和顶点坐标通常有几种方法
配方时应注意什么 公式是怎样的
二次函数y=ax2+bx+c的开口方向、对称轴、顶点坐标.
三、回顾小结
用6m长的铝合金型材做一个形状的矩形窗框,应做成长、宽各为多少时,才能使做成的窗框透光面积最大?
四、课堂练习
(1)二次函数y=-2x2+4x-1,
当x时,y随x的增大而增大,
当x时,y随x的增大而减小
(2)已知抛物线y﹦x2-4x+h的顶点A在直线y=-4x-1上,求抛物线顶点的坐标?
五、拓展延伸
22.1.4二次函数y=ax2+bx+c的图像与性质(2)二次函数的图象与字母系数a,b,c的关系复习:二次函数的概念
一般地,形如y=ax2+bx+c(a,b,c是常数,a≠0)的函数叫做二次函数.其中x是自变量,a,b,c分别为函数表达式的二次项系数、一次项系数和常数项.
导入
【注意】
(1)二次函数的表达式为整式,且二次项系数不为0;
(2)b,c可分别为0,也可同时为0;
(3)自变量的取值范围是全体实数.
第页上二次函数的图象与性质下知识讲解第页减小增大增大减小知识讲解第页二次函数的图象与字母系数a,b,c的关系上下小y左右知识讲解第页原点正负唯一两个不同没有知识讲解第页a+b+ca-b+c><知识讲解(1)二次函数y=2x2+4x-1图象的开口方向是__________(填“向上”或“向下”).
(2)已知二次函数y=x2,当x>0时,y随x的增大而__________(填“增大”或“减小”).
重难点1二次函数的图象与性质 重点
向上
增大
课堂练习
第页(3)图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是直线x=1.对于下列说法:①ab<0;②2a+b=0;③a+b+c>0;④b2-4ac<0;⑤当-1<x<3时,y>0.其中正确的是________.①②③重难点2二次函数图象与系数a,b,c的关系难点课堂练习1、二次函数的图象与性质:
(开口方向、对称轴、顶点、最值、增减性)
2、二次函数的图象与字母系数a,b,c的关系
小结
谢谢聆听
人教版九年级上册
22.1.4 二次函数y=ax2+bx+c的图象和性质(1)
一、回顾设疑
?
(x-6)+3
2
=
=(x2-12x)+21
=(x2-12x+36-36)+21
活动1:
探究二次函数的对称轴和顶点坐标
思考:
1、画出的这两个图象一样吗?
2、是什么导致了它们的不同?
3、哪一种画法正确?
4、画这种函数图象应注意什么?
二、探究新知
还可以怎样得到它的图象?
你能画出它的图象吗?
活动2:探究二次函数y=ax2+bx+c的称轴及顶点坐标
y=ax2+bx+c=
对于一般的二次函数y=ax2+bx+c,如果a>0,当x<时,
y随x的增大而减小,当x>时,y随x的增大而增大;如果a<0,
当x<时,y随x的增大而增大,当x>时,y随x的增大而减小.
归纳总结:
二次函数y=ax2+bx+c(a≠0)开口方向、对称轴、顶点坐标、增减性。
y=ax2+bx+c=
练习:
用公式法求抛物线y=-x2+2x-3的对称轴和顶点坐标。
这节课你都学到了什么?学会了哪些方法?还有什么困惑?
求二次函数y=ax2+bx+c的对称轴和顶点坐标通常有几种方法
配方时应注意什么 公式是怎样的
二次函数y=ax2+bx+c的开口方向、对称轴、顶点坐标.
三、回顾小结
用6m长的铝合金型材做一个形状的矩形窗框,应做成长、宽各为多少时,才能使做成的窗框透光面积最大?
四、课堂练习
(1)二次函数y=-2x2+4x-1,
当x时,y随x的增大而增大,
当x时,y随x的增大而减小
(2)已知抛物线y﹦x2-4x+h的顶点A在直线y=-4x-1上,求抛物线顶点的坐标?
五、拓展延伸
22.1.4二次函数y=ax2+bx+c的图像与性质(2)二次函数的图象与字母系数a,b,c的关系复习:二次函数的概念
一般地,形如y=ax2+bx+c(a,b,c是常数,a≠0)的函数叫做二次函数.其中x是自变量,a,b,c分别为函数表达式的二次项系数、一次项系数和常数项.
导入
【注意】
(1)二次函数的表达式为整式,且二次项系数不为0;
(2)b,c可分别为0,也可同时为0;
(3)自变量的取值范围是全体实数.
第页上二次函数的图象与性质下知识讲解第页减小增大增大减小知识讲解第页二次函数的图象与字母系数a,b,c的关系上下小y左右知识讲解第页原点正负唯一两个不同没有知识讲解第页a+b+ca-b+c><知识讲解(1)二次函数y=2x2+4x-1图象的开口方向是__________(填“向上”或“向下”).
(2)已知二次函数y=x2,当x>0时,y随x的增大而__________(填“增大”或“减小”).
重难点1二次函数的图象与性质 重点
向上
增大
课堂练习
第页(3)图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是直线x=1.对于下列说法:①ab<0;②2a+b=0;③a+b+c>0;④b2-4ac<0;⑤当-1<x<3时,y>0.其中正确的是________.①②③重难点2二次函数图象与系数a,b,c的关系难点课堂练习1、二次函数的图象与性质:
(开口方向、对称轴、顶点、最值、增减性)
2、二次函数的图象与字母系数a,b,c的关系
小结
谢谢聆听
同课章节目录
