第二十三章 旋转单元检测试题(含答案)
文档属性
| 名称 | 第二十三章 旋转单元检测试题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 534.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-06 10:44:40 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第二十三章 《旋转》单元测试卷
题号 一 二 三 总分
19 20 21 22 23 24
分数
一、选择题(每题3分,共30分)
1.在下图的四个图形中,不能由如图图形经过旋转或平移得到的是( )
A. B. C. D.
2.在俄罗斯方块游戏中,若某行被小方格块填满,则该行中的所有小方格会自动消失.现在游戏机屏幕下面三行已拼成如图所示的图案,屏幕上方又出现一小方格块正向下运动,为了使屏幕下面三行中的小方格都自动消失,你可以将图形进行以下的操作( )
A.先逆时针旋转90°,再向左平移 B.先顺时针旋转90°,再向左平移
C.先逆时针旋转90°,再向右平移 D.先顺时针旋转90°,再向右平移
3.如图,香港特别行政区标志紫荆花图案绕中心旋转n°后能与原来的图案互相重合,则n的最小值为( )
A.45 B.60 C.72 D.144
4.下列图案是中心对称图形的是( )
A. B. C. D.
5.下列四个图形中,既是轴对称图形又是中心对称图形的有( )个.
A.0 B.1 C.2 D.3
6.6.同学们曾玩过万花筒,它是由三块等宽等长的玻璃围成的,图是看到的万花筒的一个图案,图中所有的小三角形均是全等的等边三角形,其中的菱形可以看成是把菱形以点为中心( ).
A.顺时针旋转得到 B.顺时针旋转得到
C.逆时针旋转得到 D.逆时针旋转得到
7. 如下是一种电子计分牌呈现的数字图形,其中既是轴对称图形又是中心对称图形的是 ( )
A. B. C. D.
8. 如图,C是线段BD上一点,分别以BC、CD为边在BD同侧作等边△ABC和等边△CDE,AD交CE于F,BE交AC于G,则图中可通过旋转而相互得到的三角形对数有( ).
A.1对 B.2对 C.3对 D.4对
9. 如图所示,在正方形中,,点在上,且,点是上一动点,连接,将线段绕点逆时针旋转90°得到线段.要使点恰好落在 上, 则的长是( )
A.1 B.2 C.3 D.4
10. 如图,O是锐角三角形ABC内一点,∠AOB=∠BOC=∠COA=120°,P是△ABC内不同于O的另一点;△A′BO′、△A′BP′分别由△AOB、△APB旋转而得,旋转角都为60°,则下列结论中正确的有( ).
①△O′BO为等边三角形,且A′、O′、O、C在一条直线上.
②A′O′+O′O=AO+BO.
③A′P′+P′P=PA+PB. ④PA+PB+PC>AO+BO+CO.
A.1个 B.2个 C.3个 D.4个
二、填空题(每题3分,共24分)
11.时钟上的时针不停地旋转,从上午8时到上午11时,时针旋转的旋转角是 .
12.点(﹣2,5)关于原点对称的点的坐标是 .
13.画轴对称图形,应该先确定 ,再找出对称点,最后将对称点依次连接起来.
14.如图所示,图形①经过 变化成图形②,图形②经过 变化成图形③,图形③经过 变化成图形④.
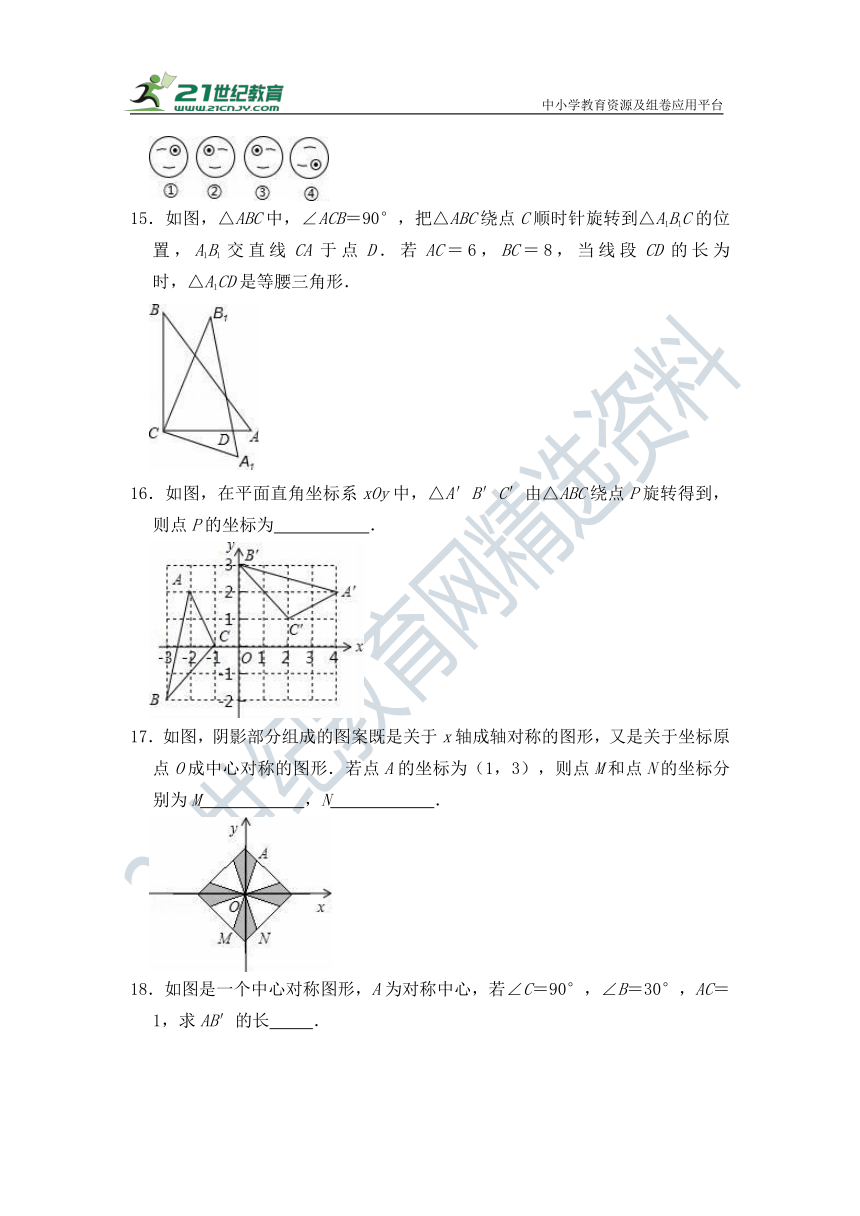
15.如图,△ABC中,∠ACB=90°,把△ABC绕点C顺时针旋转到△A1B1C的位置,A1B1交直线CA于点D.若AC=6,BC=8,当线段CD的长为 时,△A1CD是等腰三角形.
16.如图,在平面直角坐标系xOy中,△A′B′C′由△ABC绕点P旋转得到,则点P的坐标为 .
17.如图,阴影部分组成的图案既是关于x轴成轴对称的图形,又是关于坐标原点O成中心对称的图形.若点A的坐标为(1,3),则点M和点N的坐标分别为M ,N .
18.如图是一个中心对称图形,A为对称中心,若∠C=90°,∠B=30°,AC=1,求AB′的长 .
三.解答题(共46分,19题6分,20 ---24题8分)
19.如图所示,把绕点顺时针旋转,得到,交于点,若,求∠A的度数.
20.如图,点E是正方形ABCD对角线BD上的一点,且满足,将绕点A顺时针旋转90°得到,连接EC、FE.
(1)是怎样的三角形?请说明理由;
(2)试证明:点C、E、F三点在同一条直线上.
21.如图,四边形ABCD是正方形,△ADF绕着点A顺时旋转90°得到△ABE,若AF=4,AB=7.
(1)求DE的长度;
(2)指出BE与DF的关系如何?并说明由.
22.如图,已知:如图点,点在轴正半轴上,且,将线段绕点沿顺时针旋转,设点旋转后的对应点是点,求点的坐标.
23.如图,在平面直角坐标系中,有一Rt△ABC,且A(﹣1,3),B(﹣3,﹣1),
C(﹣3,3),已知△A1AC1是由△ABC旋转得到的.
(1)请写出旋转中心的坐标是 ,旋转角是 度;
(2)以(1)中的旋转中心为中心,分别画出△A1AC1顺时针旋转90°、180°的三角形;
(3)设Rt△ABC两直角边BC=a、AC=b、斜边AB=c,利用变换前后所形成的图案证明勾
股定理.
24. 已知正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上.
(1) 如图1, 连接DF、BF,若将正方形AEFG绕点A按顺时针方向旋转,判断命题:“在旋转的过程中线段DF与BF的长始终相等.”是否正确,若正确请说明理由,若不正确请举反例说明;
图1
(2) 若将正方形AEFG绕点A按顺时针方向旋转, 连接DG,在旋转的过程中,你能否找到一条线段的长与线段DG的长始终相等.并以图2为例说明理由.
图2
参考答案
一、选择题(每题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 C A C B B D C C C D
二、填空题(每题3分,共24分)
11.解:∵时针从上午的8时到11时共旋转了3个格,每相邻两个格之间的夹角是30°,
∴时针旋转的旋转角=30°×3=90°.
故答案为:90°.
12.解:根据关于原点对称的点的坐标的特点,
∴点(﹣2,5)关于原点过对称的点的坐标是(2,﹣5).
故答案为:(2,﹣5).
13.解:画轴对称图形,应该先确定对称轴,再找出对称点,最后将对称点依次连接起来.
故答案为:对称轴.
14.解:设此人从点A处登舱,逆时针旋转20分钟后到达点C.
∵旋转一周约需30分钟.某人从该摩天轮上到地面距离最近的点登舱,逆时针旋转20分钟,
∴此人旋转了×20=240°,
∴∠AOC=120°.
如图,过点O作OE⊥CD于点E,则四边形BDEO是矩形,
∴DE=OB=160﹣=83.5(米).
在直角△OEC中,∵∠COE=120°﹣90°=30°,OC==76.5米,
∴CE=OC=38.25米,
∴CD=CE+DE=38.25+83.5=121.75(米).
故答案为121.75.
15.解:三角形是等腰三角形,有如下三种情况:
①当CD=A1C=AC=6时,三角形是等腰三角形;
②当CD=A1D时,
∵∠B=90°﹣∠BCB1=∠ACB1,∠B=∠B1,
∴∠B1=∠B1CD,
∴B1D=CD.
∵CD=A1D,
∴CD=A1B1=5时,三角形是等腰三角形;
③当A1C=A1D时,如图.过点C作CE⊥A1B1于E.
∵△A1B1C的面积=×6×8=×10×CE,
∴CE=4.8.
在△A1CE中,∠A1EC=90°,由勾股定理知A1E==3.6,
∴DE=6﹣3.6=2.4.
在△CDE中,∠CED=90°,由勾股定理知CD==.
故当线段CD的长为6或5或时,△A1CD是等腰三角形.
16.解:连接AA′、CC′,
作线段AA′的垂直平分线MN,作线段CC′的垂直平分线EF,
直线MN和直线EF的交点为P,点P就是旋转中心.
∵直线MN为:x=1,设直线CC′为y=kx+b,由题意:,
∴,
∴直线CC′为y=x+,
∵直线EF⊥CC′,经过CC′中点(,),
∴直线EF为y=﹣3x+2,
由得,
∴P(1,﹣1).
故答案为(1,﹣1).
17.解:∵点M与点A关于原点对称,
∴M(﹣1,﹣3),
∵点N与点A关于x轴对称,
∴N(1,﹣3).
故答案为:(﹣1,﹣3),(1,﹣3).
18.解:∵此图是中心对称图形,A为对称中心,
∴△BAC≌△B′AC′,
∴∠B=∠B′,∠C=∠C′,AC=AC′
∵∠C=90°,∠B=30°,AC=1,
∴AB′=2AC′=2.
故答案为:2.
三.解答题(共46分,19题6分,20 ---24题8分)
19.55°
20.(1)等腰直角三角形,
21.(1)3;(2)BE=DF,BE⊥DF.
【详解】
解:(1)∵△ADF按顺时针方向旋转一定角度后得到△ABE,
∴AE=AF=4,AD=AB=7,
∴DE=AD﹣AE=7﹣4=3;
(2)BE、DF的关系为:BE=DF,BE⊥DF.理由如下:
∵△ADF按顺时针方向旋转一定角度后得到△ABE,
∴△ABE≌△ADF,
∴BE=DF,∠ABE=∠ADF,
∵∠ADF+∠F=180°﹣90°=90°,
∴∠ABE+∠F=90°,
∴BE⊥DF,
∴BE、DF的关系为:BE=DF,BE⊥DF.
22.点的坐标为.
【详解】
解:如图,作轴于,
∵,,
∴,
∵线段绕点沿逆时针旋转得,
∴,且,
∴
而,
∴,
在和中
,
∴,
∴,,
∴,
∴点的坐标为.
23.【答案】(1)O(0,0) ,旋转角是 90 (2)如图:
(3)有旋转的过程可知,四边形CC1C2C3和四边形AA1A2B是正方形.
∵S正方形CC1C2C3=S正方形AA1A2B+4S△ABC,
∴(a+b)2=c2+4×ab,即a2+2ab+b2=c2+2ab,∴a2+b2=c2.
24. 【答案】(1)不相等,用图2即可说明;
(2)BE=DG。理由:连接BE,在△ADG和△ABE中,∵AD=AB,∠∠DAG=∠BAE,AG=AE,∴ADG≌ABE(SAS),∴BE=DG。
第二十三章 《旋转》单元测试卷
题号 一 二 三 总分
19 20 21 22 23 24
分数
一、选择题(每题3分,共30分)
1.在下图的四个图形中,不能由如图图形经过旋转或平移得到的是( )
A. B. C. D.
2.在俄罗斯方块游戏中,若某行被小方格块填满,则该行中的所有小方格会自动消失.现在游戏机屏幕下面三行已拼成如图所示的图案,屏幕上方又出现一小方格块正向下运动,为了使屏幕下面三行中的小方格都自动消失,你可以将图形进行以下的操作( )
A.先逆时针旋转90°,再向左平移 B.先顺时针旋转90°,再向左平移
C.先逆时针旋转90°,再向右平移 D.先顺时针旋转90°,再向右平移
3.如图,香港特别行政区标志紫荆花图案绕中心旋转n°后能与原来的图案互相重合,则n的最小值为( )
A.45 B.60 C.72 D.144
4.下列图案是中心对称图形的是( )
A. B. C. D.
5.下列四个图形中,既是轴对称图形又是中心对称图形的有( )个.
A.0 B.1 C.2 D.3
6.6.同学们曾玩过万花筒,它是由三块等宽等长的玻璃围成的,图是看到的万花筒的一个图案,图中所有的小三角形均是全等的等边三角形,其中的菱形可以看成是把菱形以点为中心( ).
A.顺时针旋转得到 B.顺时针旋转得到
C.逆时针旋转得到 D.逆时针旋转得到
7. 如下是一种电子计分牌呈现的数字图形,其中既是轴对称图形又是中心对称图形的是 ( )
A. B. C. D.
8. 如图,C是线段BD上一点,分别以BC、CD为边在BD同侧作等边△ABC和等边△CDE,AD交CE于F,BE交AC于G,则图中可通过旋转而相互得到的三角形对数有( ).
A.1对 B.2对 C.3对 D.4对
9. 如图所示,在正方形中,,点在上,且,点是上一动点,连接,将线段绕点逆时针旋转90°得到线段.要使点恰好落在 上, 则的长是( )
A.1 B.2 C.3 D.4
10. 如图,O是锐角三角形ABC内一点,∠AOB=∠BOC=∠COA=120°,P是△ABC内不同于O的另一点;△A′BO′、△A′BP′分别由△AOB、△APB旋转而得,旋转角都为60°,则下列结论中正确的有( ).
①△O′BO为等边三角形,且A′、O′、O、C在一条直线上.
②A′O′+O′O=AO+BO.
③A′P′+P′P=PA+PB. ④PA+PB+PC>AO+BO+CO.
A.1个 B.2个 C.3个 D.4个
二、填空题(每题3分,共24分)
11.时钟上的时针不停地旋转,从上午8时到上午11时,时针旋转的旋转角是 .
12.点(﹣2,5)关于原点对称的点的坐标是 .
13.画轴对称图形,应该先确定 ,再找出对称点,最后将对称点依次连接起来.
14.如图所示,图形①经过 变化成图形②,图形②经过 变化成图形③,图形③经过 变化成图形④.
15.如图,△ABC中,∠ACB=90°,把△ABC绕点C顺时针旋转到△A1B1C的位置,A1B1交直线CA于点D.若AC=6,BC=8,当线段CD的长为 时,△A1CD是等腰三角形.
16.如图,在平面直角坐标系xOy中,△A′B′C′由△ABC绕点P旋转得到,则点P的坐标为 .
17.如图,阴影部分组成的图案既是关于x轴成轴对称的图形,又是关于坐标原点O成中心对称的图形.若点A的坐标为(1,3),则点M和点N的坐标分别为M ,N .
18.如图是一个中心对称图形,A为对称中心,若∠C=90°,∠B=30°,AC=1,求AB′的长 .
三.解答题(共46分,19题6分,20 ---24题8分)
19.如图所示,把绕点顺时针旋转,得到,交于点,若,求∠A的度数.
20.如图,点E是正方形ABCD对角线BD上的一点,且满足,将绕点A顺时针旋转90°得到,连接EC、FE.
(1)是怎样的三角形?请说明理由;
(2)试证明:点C、E、F三点在同一条直线上.
21.如图,四边形ABCD是正方形,△ADF绕着点A顺时旋转90°得到△ABE,若AF=4,AB=7.
(1)求DE的长度;
(2)指出BE与DF的关系如何?并说明由.
22.如图,已知:如图点,点在轴正半轴上,且,将线段绕点沿顺时针旋转,设点旋转后的对应点是点,求点的坐标.
23.如图,在平面直角坐标系中,有一Rt△ABC,且A(﹣1,3),B(﹣3,﹣1),
C(﹣3,3),已知△A1AC1是由△ABC旋转得到的.
(1)请写出旋转中心的坐标是 ,旋转角是 度;
(2)以(1)中的旋转中心为中心,分别画出△A1AC1顺时针旋转90°、180°的三角形;
(3)设Rt△ABC两直角边BC=a、AC=b、斜边AB=c,利用变换前后所形成的图案证明勾
股定理.
24. 已知正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上.
(1) 如图1, 连接DF、BF,若将正方形AEFG绕点A按顺时针方向旋转,判断命题:“在旋转的过程中线段DF与BF的长始终相等.”是否正确,若正确请说明理由,若不正确请举反例说明;
图1
(2) 若将正方形AEFG绕点A按顺时针方向旋转, 连接DG,在旋转的过程中,你能否找到一条线段的长与线段DG的长始终相等.并以图2为例说明理由.
图2
参考答案
一、选择题(每题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 C A C B B D C C C D
二、填空题(每题3分,共24分)
11.解:∵时针从上午的8时到11时共旋转了3个格,每相邻两个格之间的夹角是30°,
∴时针旋转的旋转角=30°×3=90°.
故答案为:90°.
12.解:根据关于原点对称的点的坐标的特点,
∴点(﹣2,5)关于原点过对称的点的坐标是(2,﹣5).
故答案为:(2,﹣5).
13.解:画轴对称图形,应该先确定对称轴,再找出对称点,最后将对称点依次连接起来.
故答案为:对称轴.
14.解:设此人从点A处登舱,逆时针旋转20分钟后到达点C.
∵旋转一周约需30分钟.某人从该摩天轮上到地面距离最近的点登舱,逆时针旋转20分钟,
∴此人旋转了×20=240°,
∴∠AOC=120°.
如图,过点O作OE⊥CD于点E,则四边形BDEO是矩形,
∴DE=OB=160﹣=83.5(米).
在直角△OEC中,∵∠COE=120°﹣90°=30°,OC==76.5米,
∴CE=OC=38.25米,
∴CD=CE+DE=38.25+83.5=121.75(米).
故答案为121.75.
15.解:三角形是等腰三角形,有如下三种情况:
①当CD=A1C=AC=6时,三角形是等腰三角形;
②当CD=A1D时,
∵∠B=90°﹣∠BCB1=∠ACB1,∠B=∠B1,
∴∠B1=∠B1CD,
∴B1D=CD.
∵CD=A1D,
∴CD=A1B1=5时,三角形是等腰三角形;
③当A1C=A1D时,如图.过点C作CE⊥A1B1于E.
∵△A1B1C的面积=×6×8=×10×CE,
∴CE=4.8.
在△A1CE中,∠A1EC=90°,由勾股定理知A1E==3.6,
∴DE=6﹣3.6=2.4.
在△CDE中,∠CED=90°,由勾股定理知CD==.
故当线段CD的长为6或5或时,△A1CD是等腰三角形.
16.解:连接AA′、CC′,
作线段AA′的垂直平分线MN,作线段CC′的垂直平分线EF,
直线MN和直线EF的交点为P,点P就是旋转中心.
∵直线MN为:x=1,设直线CC′为y=kx+b,由题意:,
∴,
∴直线CC′为y=x+,
∵直线EF⊥CC′,经过CC′中点(,),
∴直线EF为y=﹣3x+2,
由得,
∴P(1,﹣1).
故答案为(1,﹣1).
17.解:∵点M与点A关于原点对称,
∴M(﹣1,﹣3),
∵点N与点A关于x轴对称,
∴N(1,﹣3).
故答案为:(﹣1,﹣3),(1,﹣3).
18.解:∵此图是中心对称图形,A为对称中心,
∴△BAC≌△B′AC′,
∴∠B=∠B′,∠C=∠C′,AC=AC′
∵∠C=90°,∠B=30°,AC=1,
∴AB′=2AC′=2.
故答案为:2.
三.解答题(共46分,19题6分,20 ---24题8分)
19.55°
20.(1)等腰直角三角形,
21.(1)3;(2)BE=DF,BE⊥DF.
【详解】
解:(1)∵△ADF按顺时针方向旋转一定角度后得到△ABE,
∴AE=AF=4,AD=AB=7,
∴DE=AD﹣AE=7﹣4=3;
(2)BE、DF的关系为:BE=DF,BE⊥DF.理由如下:
∵△ADF按顺时针方向旋转一定角度后得到△ABE,
∴△ABE≌△ADF,
∴BE=DF,∠ABE=∠ADF,
∵∠ADF+∠F=180°﹣90°=90°,
∴∠ABE+∠F=90°,
∴BE⊥DF,
∴BE、DF的关系为:BE=DF,BE⊥DF.
22.点的坐标为.
【详解】
解:如图,作轴于,
∵,,
∴,
∵线段绕点沿逆时针旋转得,
∴,且,
∴
而,
∴,
在和中
,
∴,
∴,,
∴,
∴点的坐标为.
23.【答案】(1)O(0,0) ,旋转角是 90 (2)如图:
(3)有旋转的过程可知,四边形CC1C2C3和四边形AA1A2B是正方形.
∵S正方形CC1C2C3=S正方形AA1A2B+4S△ABC,
∴(a+b)2=c2+4×ab,即a2+2ab+b2=c2+2ab,∴a2+b2=c2.
24. 【答案】(1)不相等,用图2即可说明;
(2)BE=DG。理由:连接BE,在△ADG和△ABE中,∵AD=AB,∠∠DAG=∠BAE,AG=AE,∴ADG≌ABE(SAS),∴BE=DG。
同课章节目录
