2022--2023学年人教版 八年级数学上册12.2.2 全等三角形的判断 (SAS) 一课一练(word、含答案)
文档属性
| 名称 | 2022--2023学年人教版 八年级数学上册12.2.2 全等三角形的判断 (SAS) 一课一练(word、含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 188.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-27 18:13:14 | ||
图片预览

文档简介
人教版 八年级数学上册
12.2.2全等三角形的判断 SAS
一.选择题
1.如图,AB=AC,根据“SAS”判定△ABD≌△ACE,还需添加的条件是( )
A. BD=CE B. AD=AE
C. BO=CO D. 以上都不对
2. 如图,已知,AD⊥BC,D是BC的中点,则△ABD≌△ACD的根据是( )
A.ASA B.AAS C.SAS D.SSS
3.如图,已知AD∥BC,欲用“SAS”证明△ABC≌△CDA,需补充的条件是( )
A.AB=CD B.∠B=∠D C.AD=CB D.∠BAC=∠DCA
4.如图,AB=CD,AB∥CD,E,F是BD上两点,且BE=DF,则图中全等三角形有( )
A.1对 B.2对 C.3对 D.4对
5.如图,在△ABC与△AEF中,点F在BC上,AB=AE,BC=EF,∠B=∠E,AB交EF于点D,∠FAC=40°,则∠BFE=( )
A.35° B.40° C.45° D.50°
填空题
1.如图,已知线段AB与CD相交于点E,AC=AD,CE=ED,则图中全等三角形有 对.
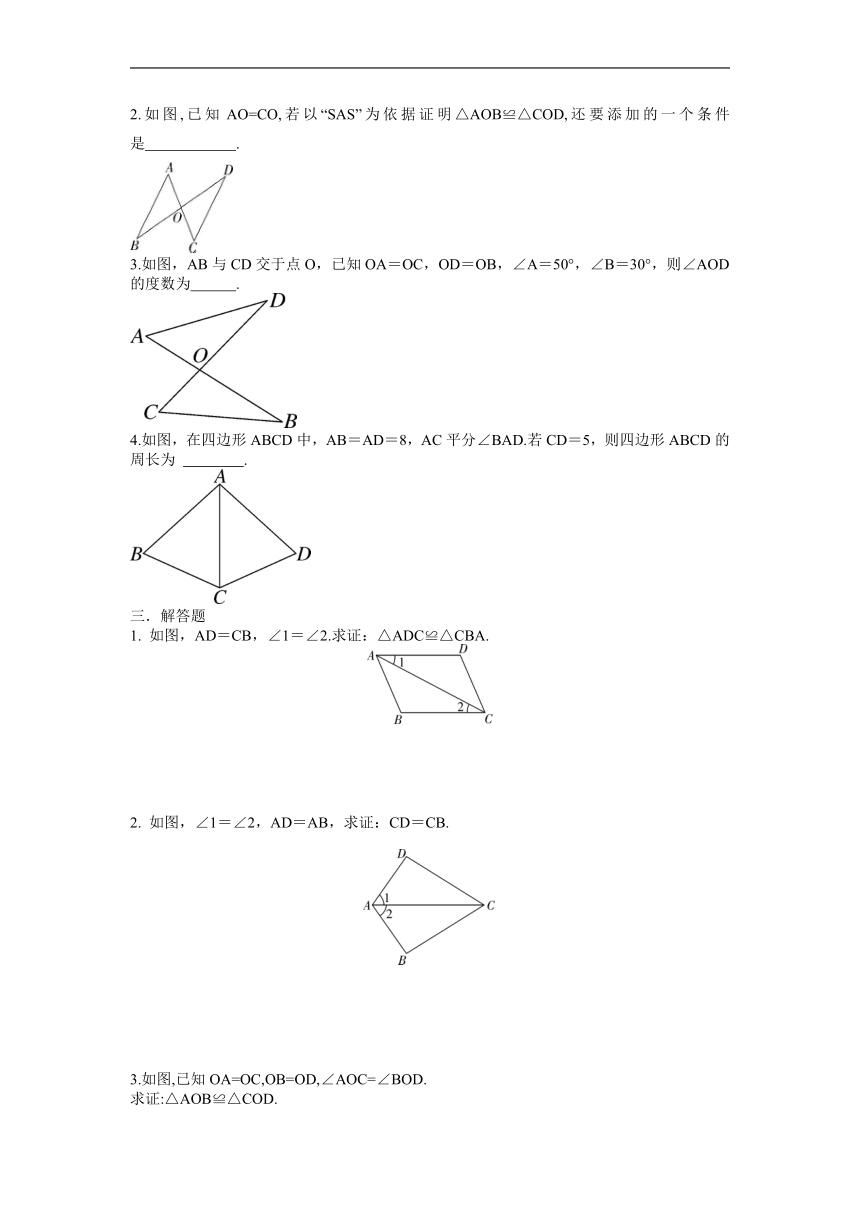
2.如图,已知AO=CO,若以“SAS”为依据证明△AOB≌△COD,还要添加的一个条件是 .
3.如图,AB与CD交于点O,已知OA=OC,OD=OB,∠A=50°,∠B=30°,则∠AOD的度数为 .
4.如图,在四边形ABCD中,AB=AD=8,AC平分∠BAD.若CD=5,则四边形ABCD的周长为 .
三.解答题
1. 如图,AD=CB,∠1=∠2.求证:△ADC≌△CBA.
2. 如图,∠1=∠2,AD=AB,求证:CD=CB.
3.如图,已知OA=OC,OB=OD,∠AOC=∠BOD.
求证:△AOB≌△COD.
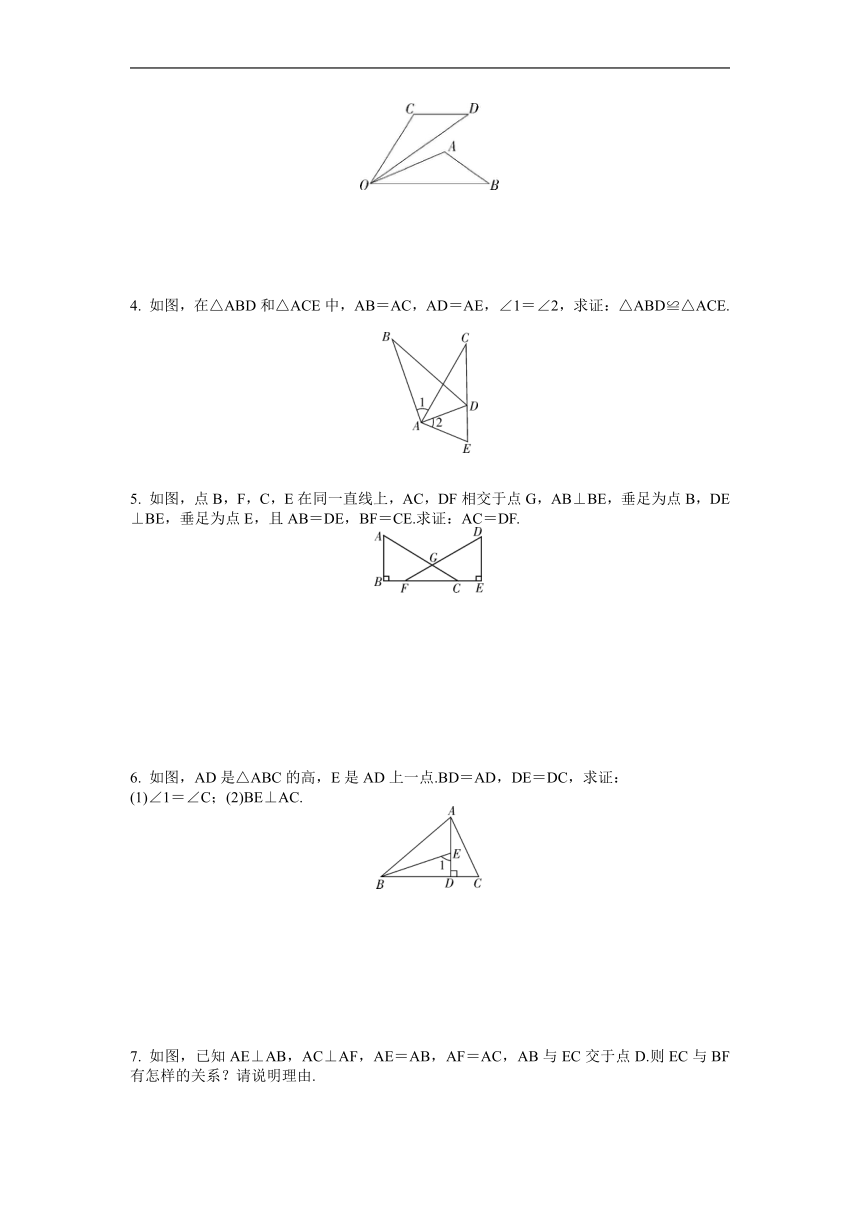
4. 如图,在△ABD和△ACE中,AB=AC,AD=AE,∠1=∠2,求证:△ABD≌△ACE.
5. 如图,点B,F,C,E在同一直线上,AC,DF相交于点G,AB⊥BE,垂足为点B,DE⊥BE,垂足为点E,且AB=DE,BF=CE.求证:AC=DF.
6. 如图,AD是△ABC的高,E是AD上一点.BD=AD,DE=DC,求证:
(1)∠1=∠C;(2)BE⊥AC.
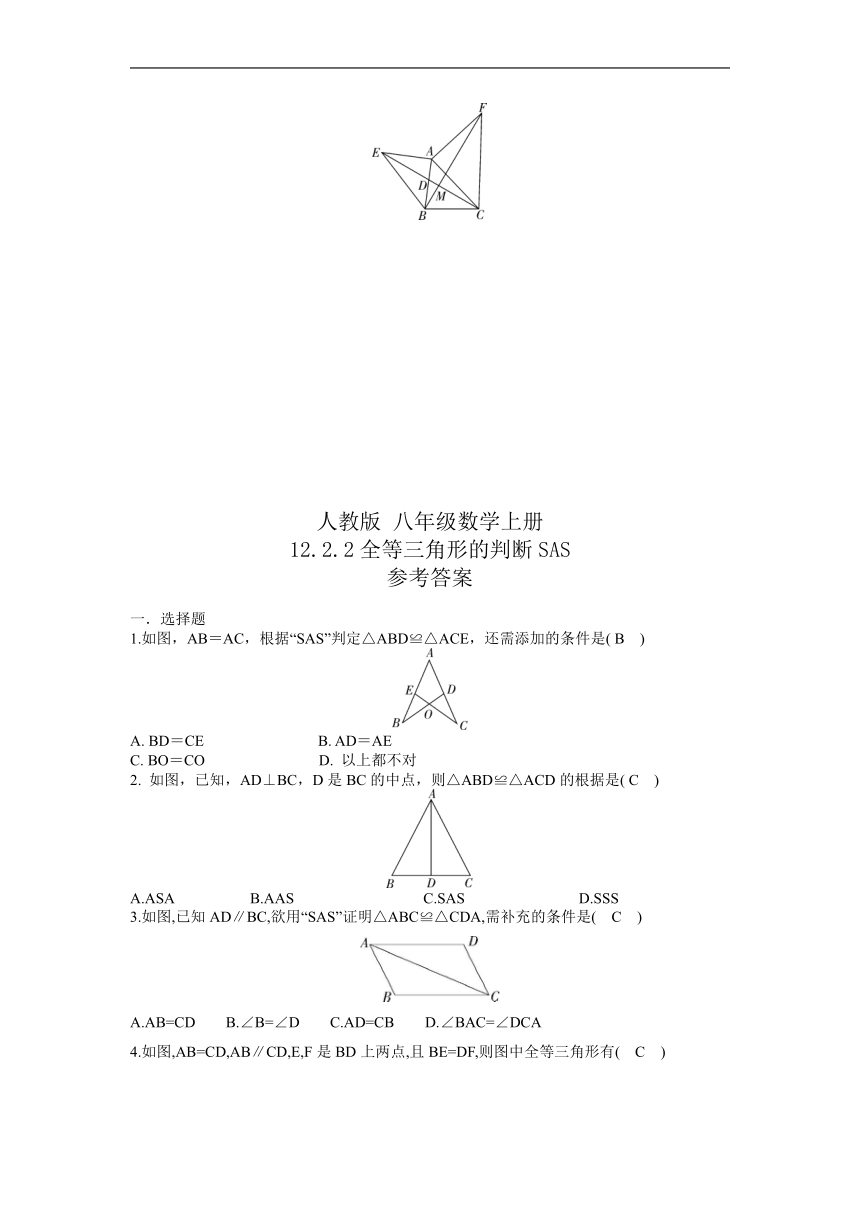
7. 如图,已知AE⊥AB,AC⊥AF,AE=AB,AF=AC,AB与EC交于点D.则EC与BF有怎样的关系?请说明理由.
人教版 八年级数学上册
12.2.2全等三角形的判断SAS
参考答案
一.选择题
1.如图,AB=AC,根据“SAS”判定△ABD≌△ACE,还需添加的条件是( B )
A. BD=CE B. AD=AE
C. BO=CO D. 以上都不对
2. 如图,已知,AD⊥BC,D是BC的中点,则△ABD≌△ACD的根据是( C )
A.ASA B.AAS C.SAS D.SSS
3.如图,已知AD∥BC,欲用“SAS”证明△ABC≌△CDA,需补充的条件是( C )
A.AB=CD B.∠B=∠D C.AD=CB D.∠BAC=∠DCA
4.如图,AB=CD,AB∥CD,E,F是BD上两点,且BE=DF,则图中全等三角形有( C )
A.1对 B.2对 C.3对 D.4对
5.如图,在△ABC与△AEF中,点F在BC上,AB=AE,BC=EF,∠B=∠E,AB交EF于点D,∠FAC=40°,则∠BFE=( B )
A.35° B.40° C.45° D.50°
二.填空题
1.如图,已知线段AB与CD相交于点E,AC=AD,CE=ED,则图中全等三角形有 3 对.
2.如图,已知AO=CO,若以“SAS”为依据证明△AOB≌△COD,还要添加的一个条件是 BO=DO .
3.如图,AB与CD交于点O,已知OA=OC,OD=OB,∠A=50°,∠B=30°,则∠AOD的度数为 100°.
4.如图,在四边形ABCD中,AB=AD=8,AC平分∠BAD.若CD=5,则四边形ABCD的周长为 26 .
三.解答题
1. 如图,AD=CB,∠1=∠2.求证:△ADC≌△CBA.
证明:在△ADC与△CBA中,
∴△ADC≌△CBA(SAS).
2. 如图,∠1=∠2,AD=AB,求证:CD=CB.
证明:在△ADC和△ABC中,
∴△ADC≌△ABC(SAS).
∴CD=CB.
3.如图,已知OA=OC,OB=OD,∠AOC=∠BOD.
求证:△AOB≌△COD.
证明 ∵∠AOC=∠BOD,
∴∠AOC-∠AOD=∠BOD-∠AOD,即∠COD=∠AOB,
在△AOB和△COD中,
∴△AOB≌△COD(SAS).
4. 如图,在△ABD和△ACE中,AB=AC,AD=AE,∠1=∠2,求证:△ABD≌△ACE.
证明:∵∠1=∠2,∴∠BAD=∠CAE.
在△ABD和△ACE中,
∴△ABD≌△ACE(SAS)
5. 如图,点B,F,C,E在同一直线上,AC,DF相交于点G,AB⊥BE,垂足为点B,DE⊥BE,垂足为点E,且AB=DE,BF=CE.求证:AC=DF.
证明:∵BF=CE,∴BF+CF=CE+CF,即BC=EF.
∵AB⊥BE,DE⊥BE,∴∠B=∠E=90°.
在△ABC和△DEF中,
∴△ABC≌△DEF(SAS). ∴AC=DF.
6. 如图,AD是△ABC的高,E是AD上一点.BD=AD,DE=DC,求证:
(1)∠1=∠C;(2)BE⊥AC.
证明:(1)∵AD⊥BC于点D,∴∠ADB=∠ADC=90°.
∵BD=AD,DE=DC,
在△BDE和△ADC中,
∴△BDE≌△ADC(SAS).∴∠1=∠C.
(2)延长BE交AC于点F,
∵△BDE≌△ADC,∴∠EBD=∠CAD.
∵∠CAD+∠C=90°,∴∠CBF+∠C=90°.
∴∠BFC=90°.∴BF⊥AC.∴BE⊥AC.
7. 如图,已知AE⊥AB,AC⊥AF,AE=AB,AF=AC,AB与EC交于点D.则EC与BF有怎样的关系?请说明理由.
解:EC=BF,EC⊥BF.
理由:∵AE⊥AB,AF⊥AC,
∴∠BAE=∠CAF=90°.
∴∠BAE+∠BAC=∠CAF+∠BAC,即∠EAC=∠BAF.
在△AEC和△ABF中,
∴△AEC≌△ABF(SAS).∴EC=BF.
∴∠AEC=∠ABF.
∵AE⊥AB,
∴∠BAE=90°.
∴∠AEC+∠ADE=90°.
∵∠ADE=∠BDM(对顶角相等),
∴∠ABF+∠BDM=90°.
在△BDM中,∠BMD=180°-(∠ABF+∠BDM)=180°-90°=90°.
∴EC⊥BF.
12.2.2全等三角形的判断 SAS
一.选择题
1.如图,AB=AC,根据“SAS”判定△ABD≌△ACE,还需添加的条件是( )
A. BD=CE B. AD=AE
C. BO=CO D. 以上都不对
2. 如图,已知,AD⊥BC,D是BC的中点,则△ABD≌△ACD的根据是( )
A.ASA B.AAS C.SAS D.SSS
3.如图,已知AD∥BC,欲用“SAS”证明△ABC≌△CDA,需补充的条件是( )
A.AB=CD B.∠B=∠D C.AD=CB D.∠BAC=∠DCA
4.如图,AB=CD,AB∥CD,E,F是BD上两点,且BE=DF,则图中全等三角形有( )
A.1对 B.2对 C.3对 D.4对
5.如图,在△ABC与△AEF中,点F在BC上,AB=AE,BC=EF,∠B=∠E,AB交EF于点D,∠FAC=40°,则∠BFE=( )
A.35° B.40° C.45° D.50°
填空题
1.如图,已知线段AB与CD相交于点E,AC=AD,CE=ED,则图中全等三角形有 对.
2.如图,已知AO=CO,若以“SAS”为依据证明△AOB≌△COD,还要添加的一个条件是 .
3.如图,AB与CD交于点O,已知OA=OC,OD=OB,∠A=50°,∠B=30°,则∠AOD的度数为 .
4.如图,在四边形ABCD中,AB=AD=8,AC平分∠BAD.若CD=5,则四边形ABCD的周长为 .
三.解答题
1. 如图,AD=CB,∠1=∠2.求证:△ADC≌△CBA.
2. 如图,∠1=∠2,AD=AB,求证:CD=CB.
3.如图,已知OA=OC,OB=OD,∠AOC=∠BOD.
求证:△AOB≌△COD.
4. 如图,在△ABD和△ACE中,AB=AC,AD=AE,∠1=∠2,求证:△ABD≌△ACE.
5. 如图,点B,F,C,E在同一直线上,AC,DF相交于点G,AB⊥BE,垂足为点B,DE⊥BE,垂足为点E,且AB=DE,BF=CE.求证:AC=DF.
6. 如图,AD是△ABC的高,E是AD上一点.BD=AD,DE=DC,求证:
(1)∠1=∠C;(2)BE⊥AC.
7. 如图,已知AE⊥AB,AC⊥AF,AE=AB,AF=AC,AB与EC交于点D.则EC与BF有怎样的关系?请说明理由.
人教版 八年级数学上册
12.2.2全等三角形的判断SAS
参考答案
一.选择题
1.如图,AB=AC,根据“SAS”判定△ABD≌△ACE,还需添加的条件是( B )
A. BD=CE B. AD=AE
C. BO=CO D. 以上都不对
2. 如图,已知,AD⊥BC,D是BC的中点,则△ABD≌△ACD的根据是( C )
A.ASA B.AAS C.SAS D.SSS
3.如图,已知AD∥BC,欲用“SAS”证明△ABC≌△CDA,需补充的条件是( C )
A.AB=CD B.∠B=∠D C.AD=CB D.∠BAC=∠DCA
4.如图,AB=CD,AB∥CD,E,F是BD上两点,且BE=DF,则图中全等三角形有( C )
A.1对 B.2对 C.3对 D.4对
5.如图,在△ABC与△AEF中,点F在BC上,AB=AE,BC=EF,∠B=∠E,AB交EF于点D,∠FAC=40°,则∠BFE=( B )
A.35° B.40° C.45° D.50°
二.填空题
1.如图,已知线段AB与CD相交于点E,AC=AD,CE=ED,则图中全等三角形有 3 对.
2.如图,已知AO=CO,若以“SAS”为依据证明△AOB≌△COD,还要添加的一个条件是 BO=DO .
3.如图,AB与CD交于点O,已知OA=OC,OD=OB,∠A=50°,∠B=30°,则∠AOD的度数为 100°.
4.如图,在四边形ABCD中,AB=AD=8,AC平分∠BAD.若CD=5,则四边形ABCD的周长为 26 .
三.解答题
1. 如图,AD=CB,∠1=∠2.求证:△ADC≌△CBA.
证明:在△ADC与△CBA中,
∴△ADC≌△CBA(SAS).
2. 如图,∠1=∠2,AD=AB,求证:CD=CB.
证明:在△ADC和△ABC中,
∴△ADC≌△ABC(SAS).
∴CD=CB.
3.如图,已知OA=OC,OB=OD,∠AOC=∠BOD.
求证:△AOB≌△COD.
证明 ∵∠AOC=∠BOD,
∴∠AOC-∠AOD=∠BOD-∠AOD,即∠COD=∠AOB,
在△AOB和△COD中,
∴△AOB≌△COD(SAS).
4. 如图,在△ABD和△ACE中,AB=AC,AD=AE,∠1=∠2,求证:△ABD≌△ACE.
证明:∵∠1=∠2,∴∠BAD=∠CAE.
在△ABD和△ACE中,
∴△ABD≌△ACE(SAS)
5. 如图,点B,F,C,E在同一直线上,AC,DF相交于点G,AB⊥BE,垂足为点B,DE⊥BE,垂足为点E,且AB=DE,BF=CE.求证:AC=DF.
证明:∵BF=CE,∴BF+CF=CE+CF,即BC=EF.
∵AB⊥BE,DE⊥BE,∴∠B=∠E=90°.
在△ABC和△DEF中,
∴△ABC≌△DEF(SAS). ∴AC=DF.
6. 如图,AD是△ABC的高,E是AD上一点.BD=AD,DE=DC,求证:
(1)∠1=∠C;(2)BE⊥AC.
证明:(1)∵AD⊥BC于点D,∴∠ADB=∠ADC=90°.
∵BD=AD,DE=DC,
在△BDE和△ADC中,
∴△BDE≌△ADC(SAS).∴∠1=∠C.
(2)延长BE交AC于点F,
∵△BDE≌△ADC,∴∠EBD=∠CAD.
∵∠CAD+∠C=90°,∴∠CBF+∠C=90°.
∴∠BFC=90°.∴BF⊥AC.∴BE⊥AC.
7. 如图,已知AE⊥AB,AC⊥AF,AE=AB,AF=AC,AB与EC交于点D.则EC与BF有怎样的关系?请说明理由.
解:EC=BF,EC⊥BF.
理由:∵AE⊥AB,AF⊥AC,
∴∠BAE=∠CAF=90°.
∴∠BAE+∠BAC=∠CAF+∠BAC,即∠EAC=∠BAF.
在△AEC和△ABF中,
∴△AEC≌△ABF(SAS).∴EC=BF.
∴∠AEC=∠ABF.
∵AE⊥AB,
∴∠BAE=90°.
∴∠AEC+∠ADE=90°.
∵∠ADE=∠BDM(对顶角相等),
∴∠ABF+∠BDM=90°.
在△BDM中,∠BMD=180°-(∠ABF+∠BDM)=180°-90°=90°.
∴EC⊥BF.
