2022—2023学年人教版数学八年级下册19.1.2 函数的图像同步练习(word、含答案)
文档属性
| 名称 | 2022—2023学年人教版数学八年级下册19.1.2 函数的图像同步练习(word、含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-27 00:00:00 | ||
图片预览

文档简介
人教版八下19.1.2 函数的图像
一、选择题(共8小题)
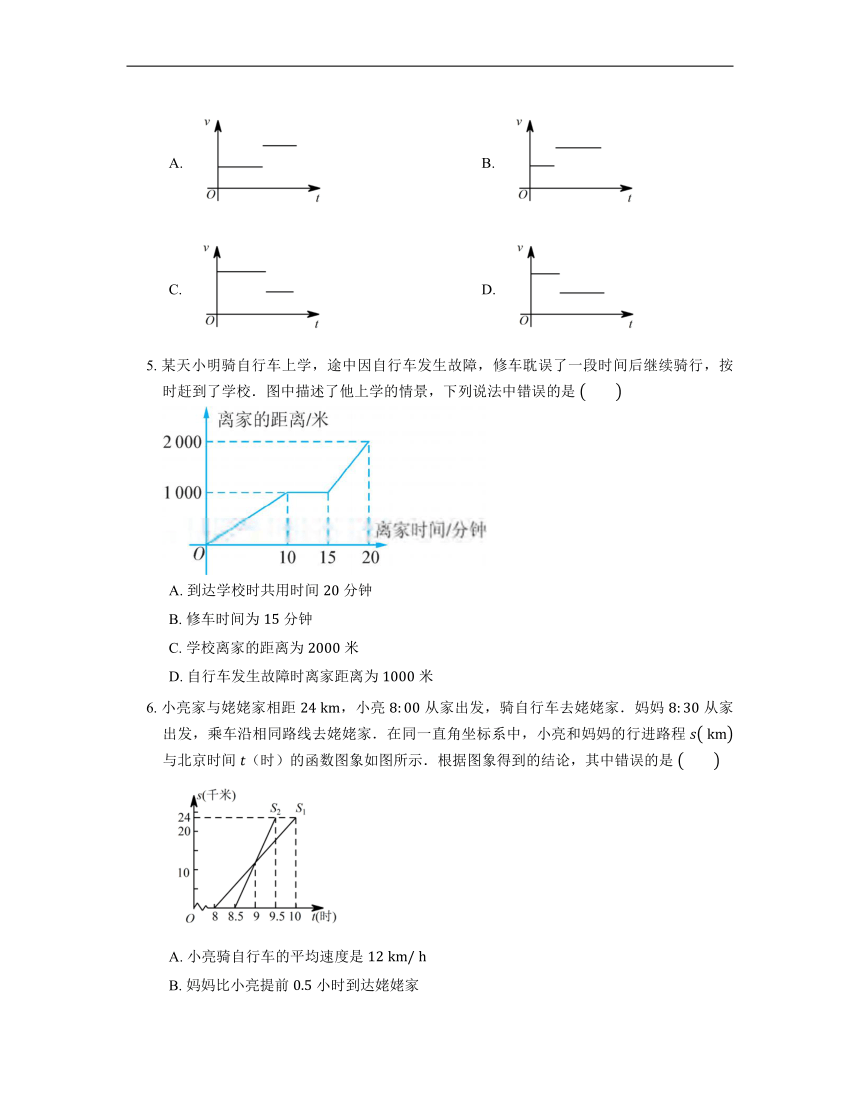
1. 小刚以 米/分的速度匀速骑车 分,在原地休息了 分,然后以 米/分的速度骑回出发地.下列函数图象能表达这一过程的是
A. B.
C. D.
2. 函数 的自变量的取值范围是
A. B.
C. 且 D.
3. 下列各图象中, 不是 的函数的是
A. B.
C. D.
4. 某人从某处出发,匀速地前进一段时间后,由于有急事,立即更快地、匀速地沿原路返回原处.这一情境中,速度 与时间 的函数图象(不考虑图象端点情况)大致为
A. B.
C. D.
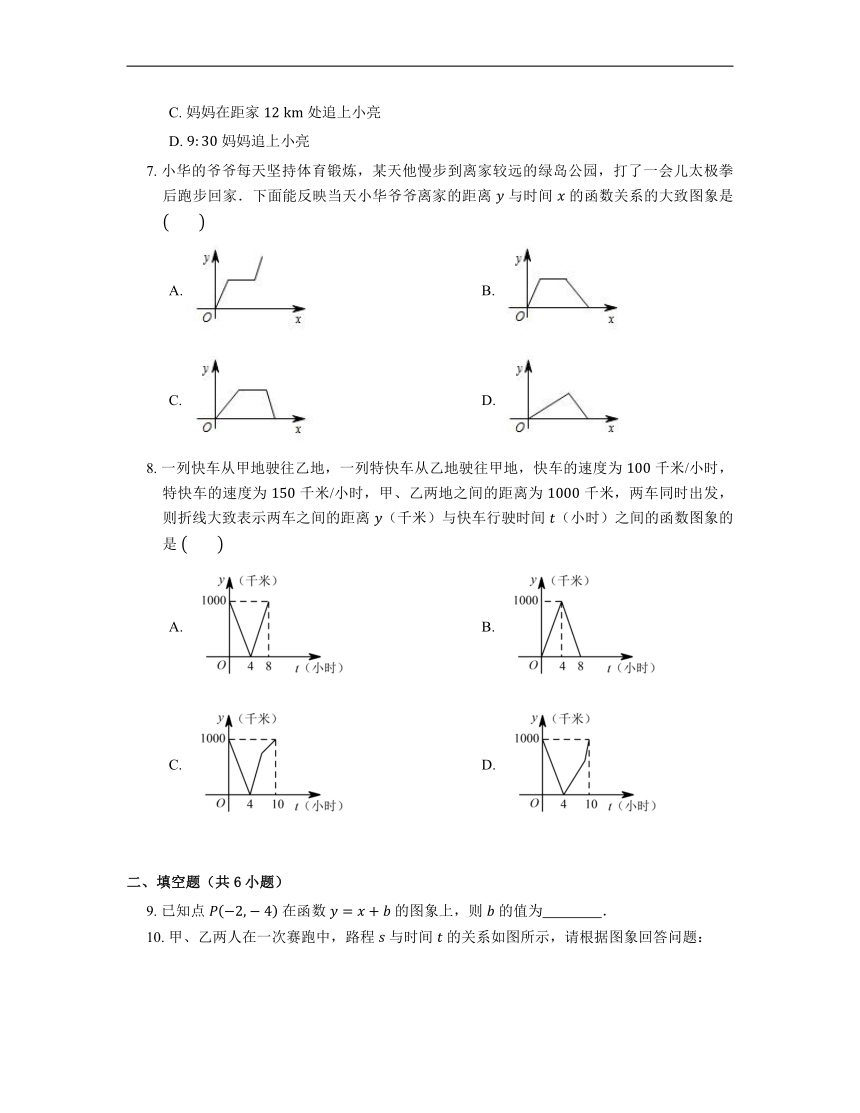
5. 某天小明骑自行车上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校.图中描述了他上学的情景,下列说法中错误的是
A. 到达学校时共用时间 分钟
B. 修车时间为 分钟
C. 学校离家的距离为 米
D. 自行车发生故障时离家距离为 米
6. 小亮家与姥姥家相距 ,小亮 从家出发,骑自行车去姥姥家.妈妈 从家出发,乘车沿相同路线去姥姥家.在同一直角坐标系中,小亮和妈妈的行进路程 与北京时间 (时)的函数图象如图所示.根据图象得到的结论,其中错误的是
A. 小亮骑自行车的平均速度是
B. 妈妈比小亮提前 小时到达姥姥家
C. 妈妈在距家 处追上小亮
D. 妈妈追上小亮
7. 小华的爷爷每天坚持体育锻炼,某天他慢步到离家较远的绿岛公园,打了一会儿太极拳后跑步回家.下面能反映当天小华爷爷离家的距离 与时间 的函数关系的大致图象是
A. B.
C. D.
8. 一列快车从甲地驶往乙地,一列特快车从乙地驶往甲地,快车的速度为 千米/小时,特快车的速度为 千米/小时,甲、乙两地之间的距离为 千米,两车同时出发,则折线大致表示两车之间的距离 (千米)与快车行驶时间 (小时)之间的函数图象的是
A. B.
C. D.
二、填空题(共6小题)
9. 已知点 在函数 的图象上,则 的值为 .
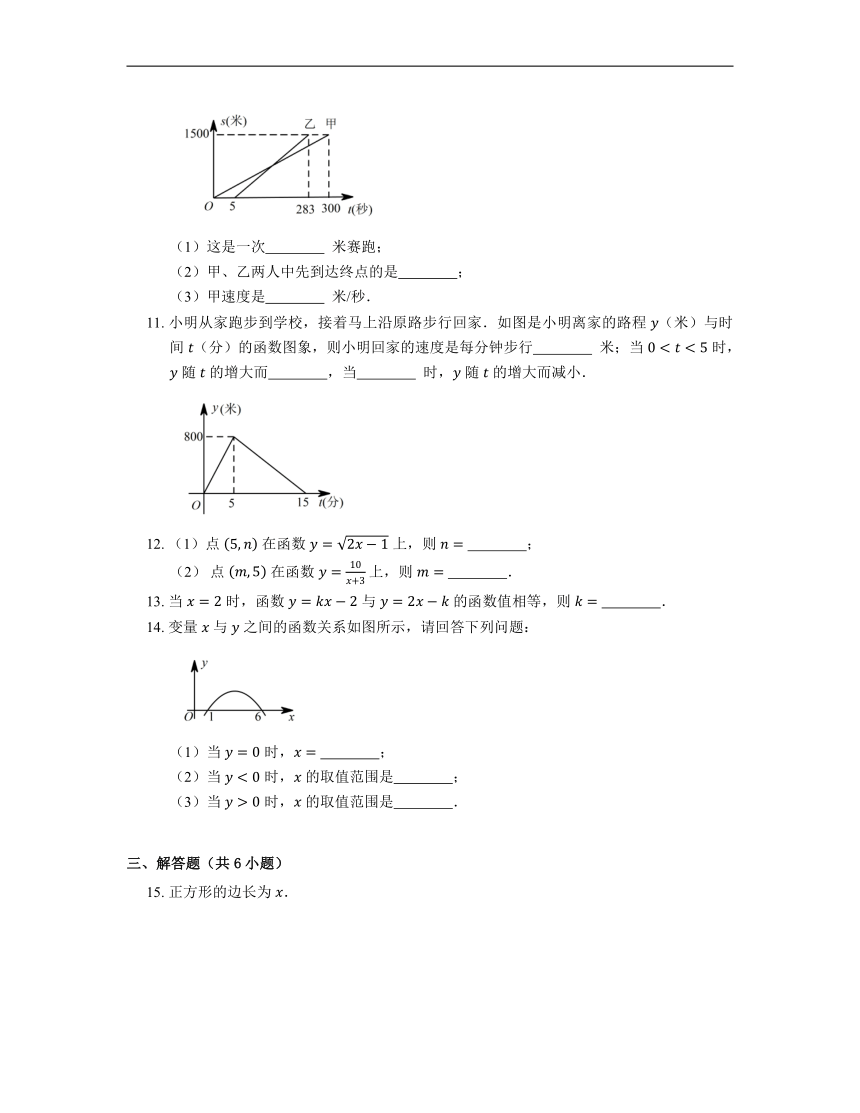
10. 甲、乙两人在一次赛跑中,路程 与时间 的关系如图所示,请根据图象回答问题:
(1)这是一次 米赛跑;
(2)甲、乙两人中先到达终点的是 ;
(3)甲速度是 米/秒.
11. 小明从家跑步到学校,接着马上沿原路步行回家.如图是小明离家的路程 (米)与时间 (分)的函数图象,则小明回家的速度是每分钟步行 米;当 时, 随 的增大而 ,当 时, 随 的增大而减小.
12. (1)点 在函数 上,则 ;
(2) 点 在函数 上,则 .
13. 当 时,函数 与 的函数值相等,则 .
14. 变量 与 之间的函数关系如图所示,请回答下列问题:
(1)当 时, ;
(2)当 时, 的取值范围是 ;
(3)当 时, 的取值范围是 .
三、解答题(共6小题)
15. 正方形的边长为 .
(1)用列表法和解析法表示正方形的周长 关于边长 的函数;
(2)用解析法和图象法表示正方形的面积 关于边长 的函数.
16. 小强骑自行车去郊游,下图是表示他离家的距离 (千米)与所用的时间 (小时)之间关系的函数图象.小强 点离家, 点回到家,根据这个图象,请你回答下列问题:
(1)小强到离家最远的地方需要几小时 此时离家有多远
(2)何时开始第一次休息 休息多长时间
(3)小强在返程中的速度是多少
17. 一个冷冻室开始的温度是 ,开机降温后室温每小时下降 ,设 表示开机降温工作 时的温度.
(1)写出 与 之间的函数关系式;
(2)说明经过几小时冷冻室温度降至 何时降至
18. 学校为创建多媒体教学中心,备有资金 万元,已分批购进电脑 台,每台电脑单价 元.
(1)求所剩资金 (万元)与购进电脑台数 (台)之间的函数关系式,并求自变量的取值范围;
(2)购入 台这种型号的电脑后还剩余多少万元资金
19. 某商店零售一种商品,其质量 与售价 (元)之间的关系如下表:
(根据销售经验,顾客在此处零买商品均未超过 .)
(1)由上表推出售价 (元)随质量 变化的函数关系式,并画出函数的图象;
(2)顾客购买这种商品 应付多少元
20. 某学校开展“青少年科技创新比赛”活动,“喜洋洋”代表队设计了一个遥控车沿直线轨道 做匀速直线运动的模型.甲、乙两车同时分别从 , 出发,沿轨道到达 处,在 上,甲的速度是乙的速度的 倍,设 (分)后甲、乙两遥控车与 处的距离分别为 ,,则 , 与 的函数关系如图,试根据图象解决下列问题:
(1)填空:乙的速度 米/分;
(2)写出 与 的函数关系式;
(3)若甲、乙两遥控车的距离超过 米时信号不会产生相互干扰,试探求什么时间两遥控车的信号不会产生相互干扰
答案
1. C
2. C
3. A
4. A
5. B
6. D
7. C
【解析】此图象为三段,一是慢步到公园( 增大),二是在公园打太极拳( 不变),三是跑步回家( 减少).
8. C
9.
10. ,乙,
11. ,增大,
12. ,
13.
14. 或 , 或 ,
15. (1) 用列表法表示正方形的周长 关于边长 的函数如下:
用解析法表示正方形的周长 关于边长 的函数为:
.
(2) 用解析法表示正方形的面积 关于边长 的函数为:;
用图象法表示正方形的面积 关于边长 的函数如下图所示:
16. (1) 小时; 千米.
(2) 在 时开始第一次休息;休息 小时.
(3) 千米/时.
17. (1) .
(2) 小时; 小时.
18. (1) 由题意得 ,要使此式符合题意, 必须是不小于 的整数,且 ,即 解得 ,且 为整数,
所以 与 之间的函数关系式为 ,自变量 的取值范围是 ,且 为整数.
(2) 当 时,(万元),
所以购入 台这种型号的电脑后还剩余 万元资金.
19. (1) .
图象:
(2) 元.
20. (1)
(2) .
(3) 当 或 时,两车的信号不会产生相互干扰.
一、选择题(共8小题)
1. 小刚以 米/分的速度匀速骑车 分,在原地休息了 分,然后以 米/分的速度骑回出发地.下列函数图象能表达这一过程的是
A. B.
C. D.
2. 函数 的自变量的取值范围是
A. B.
C. 且 D.
3. 下列各图象中, 不是 的函数的是
A. B.
C. D.
4. 某人从某处出发,匀速地前进一段时间后,由于有急事,立即更快地、匀速地沿原路返回原处.这一情境中,速度 与时间 的函数图象(不考虑图象端点情况)大致为
A. B.
C. D.
5. 某天小明骑自行车上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校.图中描述了他上学的情景,下列说法中错误的是
A. 到达学校时共用时间 分钟
B. 修车时间为 分钟
C. 学校离家的距离为 米
D. 自行车发生故障时离家距离为 米
6. 小亮家与姥姥家相距 ,小亮 从家出发,骑自行车去姥姥家.妈妈 从家出发,乘车沿相同路线去姥姥家.在同一直角坐标系中,小亮和妈妈的行进路程 与北京时间 (时)的函数图象如图所示.根据图象得到的结论,其中错误的是
A. 小亮骑自行车的平均速度是
B. 妈妈比小亮提前 小时到达姥姥家
C. 妈妈在距家 处追上小亮
D. 妈妈追上小亮
7. 小华的爷爷每天坚持体育锻炼,某天他慢步到离家较远的绿岛公园,打了一会儿太极拳后跑步回家.下面能反映当天小华爷爷离家的距离 与时间 的函数关系的大致图象是
A. B.
C. D.
8. 一列快车从甲地驶往乙地,一列特快车从乙地驶往甲地,快车的速度为 千米/小时,特快车的速度为 千米/小时,甲、乙两地之间的距离为 千米,两车同时出发,则折线大致表示两车之间的距离 (千米)与快车行驶时间 (小时)之间的函数图象的是
A. B.
C. D.
二、填空题(共6小题)
9. 已知点 在函数 的图象上,则 的值为 .
10. 甲、乙两人在一次赛跑中,路程 与时间 的关系如图所示,请根据图象回答问题:
(1)这是一次 米赛跑;
(2)甲、乙两人中先到达终点的是 ;
(3)甲速度是 米/秒.
11. 小明从家跑步到学校,接着马上沿原路步行回家.如图是小明离家的路程 (米)与时间 (分)的函数图象,则小明回家的速度是每分钟步行 米;当 时, 随 的增大而 ,当 时, 随 的增大而减小.
12. (1)点 在函数 上,则 ;
(2) 点 在函数 上,则 .
13. 当 时,函数 与 的函数值相等,则 .
14. 变量 与 之间的函数关系如图所示,请回答下列问题:
(1)当 时, ;
(2)当 时, 的取值范围是 ;
(3)当 时, 的取值范围是 .
三、解答题(共6小题)
15. 正方形的边长为 .
(1)用列表法和解析法表示正方形的周长 关于边长 的函数;
(2)用解析法和图象法表示正方形的面积 关于边长 的函数.
16. 小强骑自行车去郊游,下图是表示他离家的距离 (千米)与所用的时间 (小时)之间关系的函数图象.小强 点离家, 点回到家,根据这个图象,请你回答下列问题:
(1)小强到离家最远的地方需要几小时 此时离家有多远
(2)何时开始第一次休息 休息多长时间
(3)小强在返程中的速度是多少
17. 一个冷冻室开始的温度是 ,开机降温后室温每小时下降 ,设 表示开机降温工作 时的温度.
(1)写出 与 之间的函数关系式;
(2)说明经过几小时冷冻室温度降至 何时降至
18. 学校为创建多媒体教学中心,备有资金 万元,已分批购进电脑 台,每台电脑单价 元.
(1)求所剩资金 (万元)与购进电脑台数 (台)之间的函数关系式,并求自变量的取值范围;
(2)购入 台这种型号的电脑后还剩余多少万元资金
19. 某商店零售一种商品,其质量 与售价 (元)之间的关系如下表:
(根据销售经验,顾客在此处零买商品均未超过 .)
(1)由上表推出售价 (元)随质量 变化的函数关系式,并画出函数的图象;
(2)顾客购买这种商品 应付多少元
20. 某学校开展“青少年科技创新比赛”活动,“喜洋洋”代表队设计了一个遥控车沿直线轨道 做匀速直线运动的模型.甲、乙两车同时分别从 , 出发,沿轨道到达 处,在 上,甲的速度是乙的速度的 倍,设 (分)后甲、乙两遥控车与 处的距离分别为 ,,则 , 与 的函数关系如图,试根据图象解决下列问题:
(1)填空:乙的速度 米/分;
(2)写出 与 的函数关系式;
(3)若甲、乙两遥控车的距离超过 米时信号不会产生相互干扰,试探求什么时间两遥控车的信号不会产生相互干扰
答案
1. C
2. C
3. A
4. A
5. B
6. D
7. C
【解析】此图象为三段,一是慢步到公园( 增大),二是在公园打太极拳( 不变),三是跑步回家( 减少).
8. C
9.
10. ,乙,
11. ,增大,
12. ,
13.
14. 或 , 或 ,
15. (1) 用列表法表示正方形的周长 关于边长 的函数如下:
用解析法表示正方形的周长 关于边长 的函数为:
.
(2) 用解析法表示正方形的面积 关于边长 的函数为:;
用图象法表示正方形的面积 关于边长 的函数如下图所示:
16. (1) 小时; 千米.
(2) 在 时开始第一次休息;休息 小时.
(3) 千米/时.
17. (1) .
(2) 小时; 小时.
18. (1) 由题意得 ,要使此式符合题意, 必须是不小于 的整数,且 ,即 解得 ,且 为整数,
所以 与 之间的函数关系式为 ,自变量 的取值范围是 ,且 为整数.
(2) 当 时,(万元),
所以购入 台这种型号的电脑后还剩余 万元资金.
19. (1) .
图象:
(2) 元.
20. (1)
(2) .
(3) 当 或 时,两车的信号不会产生相互干扰.
